基于NSGA-II算法的八連桿機械壓力機桿系設計
袁良照, 翟華,2,張蘭軍,高廣權,王玉山
(1.合肥工業大學工業與裝備技術研究院,安徽 合肥230009; 2.合肥工業大學機械與汽車工程學院,安徽 合肥,230009; 3.合肥合鍛智能制造股份有限公司,安徽 合肥,230601)
基于NSGA-II算法的八連桿機械壓力機桿系設計
袁良照1, 翟華1,2,張蘭軍3,高廣權3,王玉山3
(1.合肥工業大學工業與裝備技術研究院,安徽 合肥230009; 2.合肥工業大學機械與汽車工程學院,安徽 合肥,230009; 3.合肥合鍛智能制造股份有限公司,安徽 合肥,230601)
針對閉式四點八連桿機械壓力機工藝行程精密設計要求,綜合考慮拉延速度穩定的工作品質,提出以壓力機行程設計誤差最小和工作行程拉延速度波動量小的多目標函數,以機構動力學特性為約束條件,建立八連桿機械壓力機桿系優化數學模型。采用帶精英策略的非占優排序遺傳算法NSGA-II對含有12個優化變量的數學模型進行優化,保證行程設計誤差最小為第一附加準則,在pareto最優解中確定最終桿系參數。優化實例表明該方法可以為閉式四點八連桿機械壓力機復雜桿系快速設計提供參考。
機械壓力機;八連桿;NSGA-II;優化
0 前言
閉式四點機械壓力機可以完成拉延、擠壓、粉末成形和沖裁等多種成形工藝。廣泛應用在汽車制造、家電生產、建筑行業、化工石油等重要領域。目前國內機械壓力機的設計仍以類比設計和經驗設計為主要方法,導致設計結果與實際要求差異較大,設計效率低下[1-7]。
在機械壓力機優化方面,有很多學者進行了相關研究。孫昕煜[8]利用步長搜索對一種新型多連桿壓力機各桿結構尺寸進行優化,結果表明滑塊在下死點附近,速度曲線相對平緩,進程和回程速度快。李初曄[9]基于ANSYS-APDL對八連桿壓力機桿系進行了優化,優化后滑塊速度平穩,滑塊行程及拉延速度皆滿足設計要求。余發國[10]使用復合形法對八連桿機械壓力機桿系進行優化,提出了桿系不干涉條件判據。王曉麗[11]用步長搜索法對壓力機八桿內滑塊機構進行優化設計,結果表明最大壓力角比原機構減小6.4°,運動學性能明顯改善。范云霄[12]建立了多連桿壓力機傳動機構的虛擬樣機, 以滑塊在工作行程內速度波動量最小為目標函數建立優化數學模型,結果表明滑塊在拉伸區內速度波動量較小。何予鵬[18]采用遺傳算法對六連桿壓力機桿系進行優化,優化后該壓力機與典型機械壓力機相比,其工作性能有明顯的提高。
上述研究在探討壓力機桿系優化上取得了一定的成果,但是針對任意行程復雜八連桿壓力機桿系設計中缺乏適用性,尚無實用方法應用于工程實際。
八連桿機械壓力機主要用于金屬薄板件拉延工藝,由于桿系構件多,桿系設計復雜,且主要依靠經驗設計,設計效率低。本文構建八連桿機械壓力機桿系多目標優化數學模型,重點考慮壓力機工藝行程精密設計要求和工作拉延速度穩定性,結合動力學約束條件,采用帶精英策略的非占優排序遺傳算法NSGA-II,對運動桿系進行優化設計,從而得到滿足工藝曲線和速度穩定性要求的桿系中各桿件尺寸。
1 八連桿桿系運動分析
圖1是八連桿運動桿系結構示意圖。桿l1是主動件,以角速度ω1逆時針方向勻速轉動,通過其余各桿傳動,實現滑塊在豎直方向的上下運動。其中桿l3與桿l4夾角θ1以及桿l6與桿l7夾角θ2固定,形成兩個Ⅲ級組。點O1和O2為固定支點,σ為桿l2與桿l3之間的夾角,φ1、φ2、φ3、φ4、φ5、φ6、φ7、φ8分別對應桿l1、l2、l3、l4、l5、l6、l7、l8的轉角。為減小分析的難度,將運動桿系看成三個模塊,分別為O1AB2O1,O1ADC2O1,O1AEFO1。
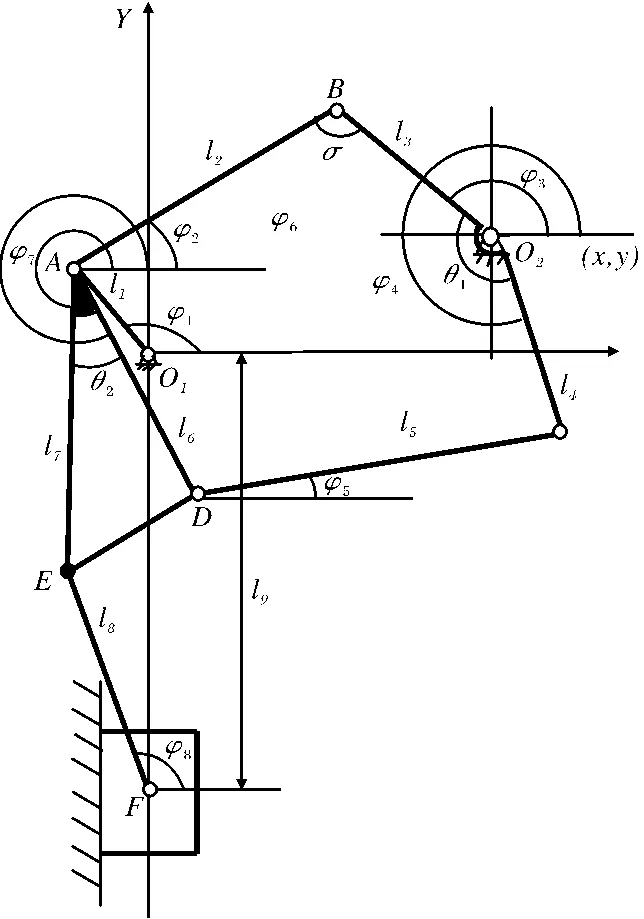
圖1 八連桿機械壓力機運動桿系結構示意圖
運用矩陣求解三個模塊的運動學公式。設l1,l2,l3,l4,l5,l6,l7,l8分別為各桿的矢量,l9為滑塊在豎直方向上位移的矢量,由此得
(1)
式(1)中的各矢量分別對圖1中的x、y坐標軸投影,得下式
(2)
式(2)對時間t求導,可得速度關系如下式:
(3)
式中,
再將式(3)對時間t求導可得加速度關系
(4)
式中,
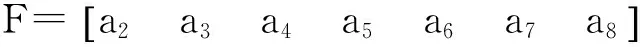
φ4=φ3+θ1
φ1=φ6+θ2
故有
ω4=ω3,ω6=ω7,a4=a3,a6=a7
(5)
下死點位置是桿l1、l7、l8共線處,此時滑塊處于最遠的極限位置,取滑塊下死點為滑塊位移S的計算起點。則有滑塊位移方程:
S=l1+l7+l8-l9
(6)
根據以上各式,將已知參數代入,即可計算滑塊的速度、位移、加速度運動曲線圖。
2 八連桿機械壓力機運動桿系優化數學模型
根據被加工零件的拉延工藝,機械壓力機滑塊的位移、速度、加速度需要符合設計要求,因此影響滑塊位移和運動性能的12個參數l1,l2,l3,l4,l5,l6,l7,l8,x,y,θ1,θ2確定為設計變量X,即
X=[l1,l2,l3,l4,l5,l6,l7,l8,x,y,θ1,θ2]T
=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12]T
八連桿壓力機工作時,要求滑塊在工作行程階段速度較低且保持均勻,從而有利于拉延成形[1],即以工作行程速度波動量最小為目標函數一f1(X),現規定桿l1起始點為下死點處,工作行程時間為[t1,t2],對該段時間速度取方差
(7)
式中,k為時間段[t1,t2]分割段數。
八連桿壓力機行程是壓力機設計的重要指標,因此必須確保設計行程和目標行程大小一致,以目標行程和設計行程差值的平方最小為目標函數二f2(X)。
minf2(X)=(S-Sd)2
(8)
式中,S為目標行程,Sd為設計行程。
桿l1是曲柄,由桿l1的轉動帶動其余桿轉動實現滑塊的上下運動,依據曲柄存在條件[19],提出如下約束條件
g1(X)=l2-l1>0
g2(X)=l3-l1>0
(9)
為確保機構具有良好的動力學特性,桿l2和桿l3的夾角需滿足40°≤σ≤140°,σmax、σmin的余弦公式
故有約束條件
g7(X)=cosσmin-cos40°≤0
(10)
g8(X)=cosσmax-cos140°≥0
3 八連桿壓力機運動桿系NSGA-II算法
采用目標規劃法求解多個優化目標問題,目標規劃法是基于各個目標函數期望值進行優化,該方法追求目標函數值與期望值的絕對誤差累加之和最小。即
(11)
Gi(X)是每個目標函數的期望值,fi(X)是目標函數。
所用算法為基于Pareto方法的帶精英策略的非支配排序遺傳算法NSGA-II,該算法的具體過程描述如下[13]:
(1)令初始時間t=0,隨機產生初始種群P0,然后對種群進行非劣解排序,每個個體被賦予秩;再對初始種群進行二元錦標賽選擇、交叉和變異,得到新的種群Q0;
(2)形成新的群體R1=Pt∪Qt,對種群Rt進行非劣解排序,得到非劣前端F1,F2……;
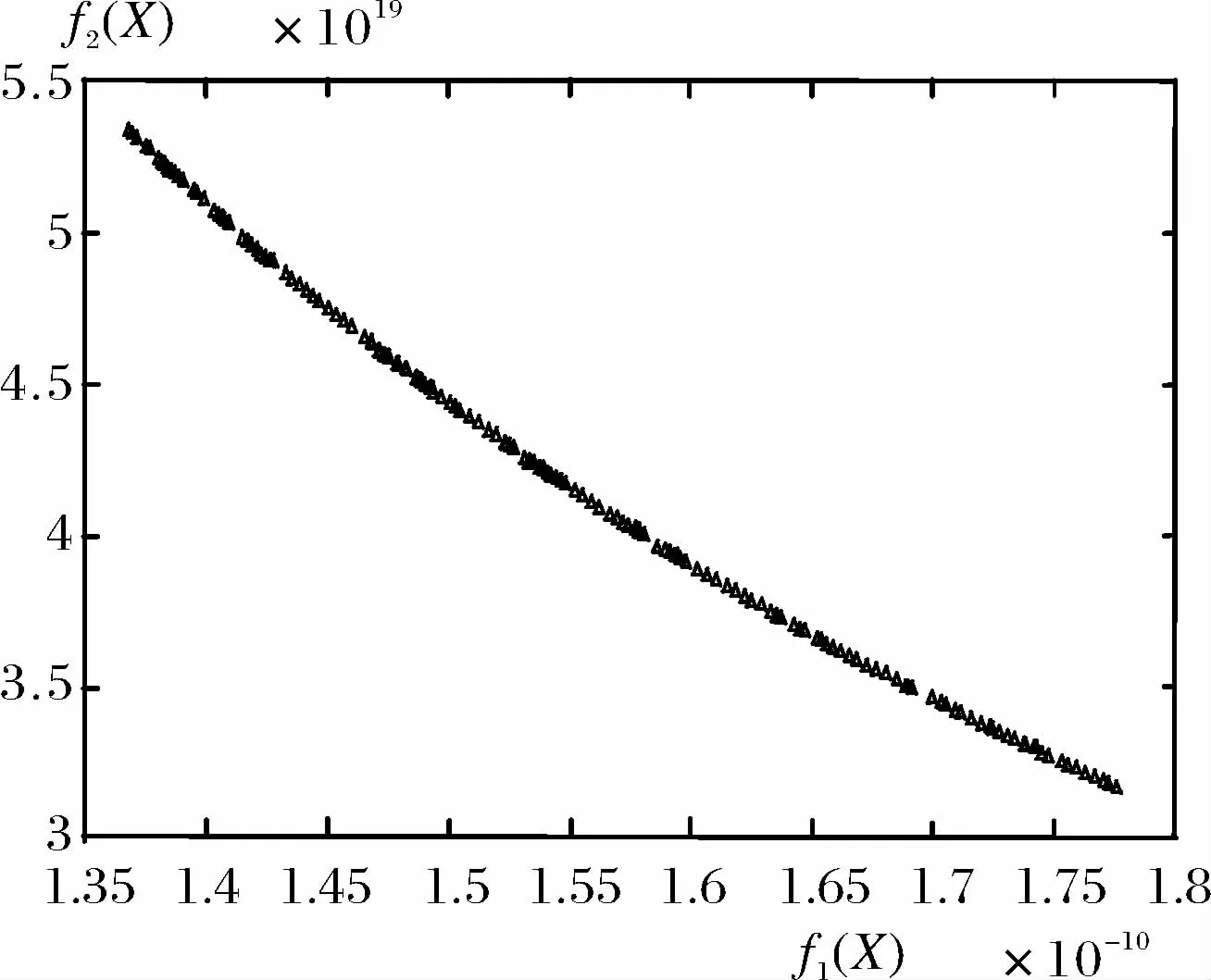
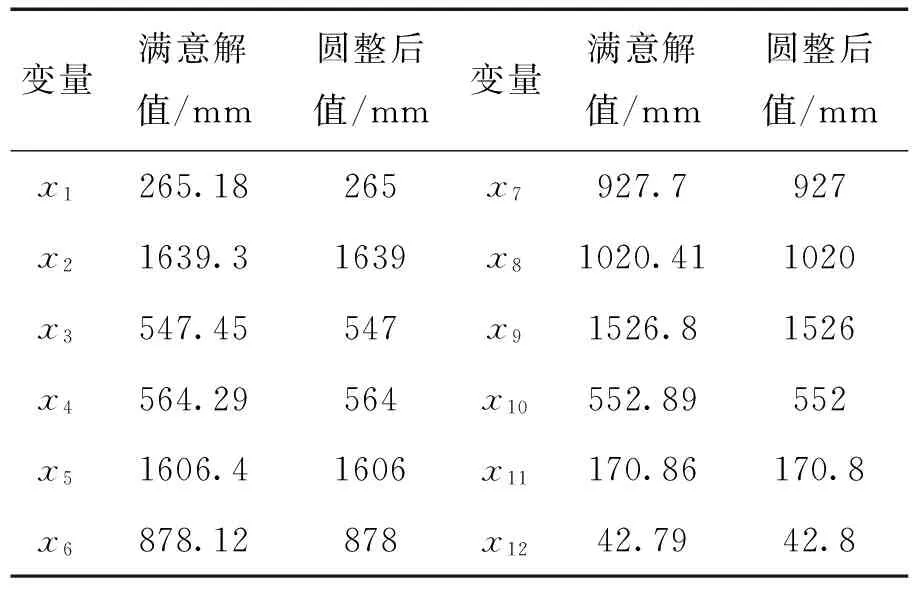
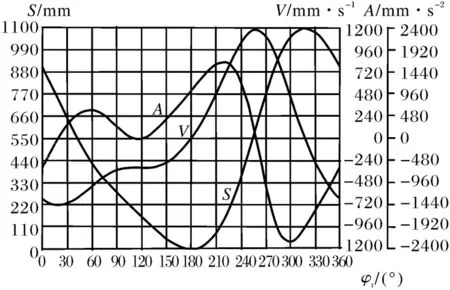
(3)對所有Fi按擁擠比較操作 (4)對種群Pt+1執行復制、交叉和變異,形成種群Qt+1; (5)如果終止條件成立,則結束;否則,t=t+1,轉到(2); 遺傳算法中使用適應度概念評估種群中每個個體在優化過程中可能達到或接近于找到最優解的優劣程度。F1(X)、F2(X)分別為目標函數f1(X)、f2(X)對應的適應度函數。根據優化目標最小提出以下適應度函數形式: (12) 遺傳算法必須對約束條件進行處理,但是目前并沒有對約束條件處理的一般方法。本文采用罰函數法與NSGA-II相結合解決了多個約束條件對算法尋優的不利影響。罰函數法的基本思想是:計算解空間中無對應可行解個體的適應度值時,將懲罰項加到目標函數中,以降低該個體適應度值,將含有約束的優化問題轉化為無約束問題。即 (1)當變量X滿足約束條件時有 (13) (2)當變量X不滿足約束條件時有 (14) (15) 式中,r為懲罰因子,gu(X)、hj(X)分別是不等式約束和等式約束。 多目標優化問題的解是一組均衡解,稱為最優非劣解集或Pareto最優解集。遺傳算法通過代表整個解集的種群優化,以內在并行方式搜索多個非劣解,為決策者提供多個選擇方案。Pareto最優解集中每個解都是多目標優化問題的一個非劣解。實際問題應用中仍需從多個Pareto最優解中選擇一個符合實際和決策者偏好的滿意解。在Pareto最優解集中選擇最終桿系參數時應以設計行程接近目標行程為第一附加準則,可通過比較解集中每組解的適應度值大小縮小選擇范圍,進行仿真驗證。 八連桿機械壓力機目標行程Sd=1 100mm,以已有同行程閉式四點機械壓力機為參考,變量可行域下限設為lb=[210 1600 500 550 1550 850 900 980 1480 500 170 40];可行域上限設為ub=[280 1700 600 650 1650 950 1000 1080 1580 600 179 50],懲罰因子r=1000,算法設置初始種群個數150,交叉概率0.95,變異概率隨著遺傳代數增加自適應變化,算法多次迭代至300代左右個體進化陷入停滯,在MATLAB軟件中運行算法,運算完畢得到含有多組解的Pareto最優解集,圖2所示為該問題的最終Pareto前沿分布示意圖,目標函數f1(X)和f2(X)均為越小越優。 圖2 目標行程1100mm八連桿桿系Pareto前沿圖 通過對比每組解目標函數f2(X)的值大小,從小到大依次進行仿真驗證,鑒于進化類算法隨機性特點以及變量可行域設置的影響,本文所要求的滿意解會出現在目標函數f2(X)取最小值或略大于最小值附近位置。通過對比可得滿意解如表1中第1行數據。對這組解進行圓整,圓整后分別對應表1中第2行數據解。 表1 目標行程1 100 mm八連桿機械壓力機滿意解 對表1中數據圓整后值進行運動仿真計算,得運動曲線和軌跡曲線,如圖3所示,圖中A線表示滑塊加速度,V線表示滑塊速度,S線表示滑塊位移。由圖中可以看出,在工作區間內滑塊速度波動量較小,速度曲線較為平緩,行程大小都符合設計要求。 圖3 表1圓整后仿真曲線示意圖 仿真實驗列舉了目標行程1 100 mm八連桿桿系設計過程。搜索空間的形狀對目標規劃法的計算結果影響十分明顯,多次實驗結果證明,變量x11,x12的搜索區間對算法最終能否順利尋優影響較大,十二個變量根據不同的目標行程,確定不同的搜索區間。 實驗結果表明,遺傳算法控制參數選擇非常關鍵。選擇過大過小的交叉概率都不利于種群的進化,變異概率的選擇則是基于防止優良個體因變異被破壞,以及陷入局部最優為準則。 表1是以符合目標行程為第一附加準則選出的一組Pareto最優解,通過仿真驗證得到運動曲線圖2,觀察運動曲線可以得出該組解符合目標行程要求,滑塊工作區間內速度波動量小,且速度值較低,能完成拉延工藝,滑塊回程階段則速度值明顯較快,有效提高八連桿壓力機的工作效率。經過驗證該方法對于行程1 200 mm以及行程1 400 mm的八連桿機械壓力機也同樣適用。 該方法已經應用到合肥合鍛機床股份有限公司閉式四點八連桿機械壓力機桿系設計中,如圖3是行程1 200 mm的閉式四點八連桿機械壓力機,設計結果可以滿足壓力機工藝行程精密設計和工作拉延速度穩定性設計要求。同時桿系設計時間由過去的6周縮短為1周,提高了設計效率,減少了設計周期。 圖3 采用NSGA-II算法設計桿系的機械壓力機 主要針對八連桿壓力機主傳動桿系優化過程,提出一種基于NSGA-II算法的優化方法,在僅知閉式四點機械壓力機目標行程的條件下,可以快速提供桿系參數選擇方案,能夠有效保證工作行程內滑塊的速度波動量符合使用要求,桿系設計時間由過去的6周可以縮短為1周,提高了設計效率,減少了設計周期。為多連桿設計提供參考價值。 [1] 孫靖民,梁迎春.機械優化設計[M].北京:機械工業出版社,2015. [2] Radovan R. Bulatovi,Stevan R.Optimal synthesis of a path generator six-bar linkage[J]. Journal of Mechanical Science and Technology,2012,26 (12):4027-4040. [3] R. Sancibrian. Improved GRG method for the optimal synthesis of linkages in function generation problems[J]. Mechanism and Machine Theory,2011,46(06):1350-1375. [4] GUO Weizhong,GAO Feng Design of a Servo Mechanical Press with Redundant Actuation[J] .Chinese Journal Of Mechanical Engineering,2009, 22(04):574-579. [5] J.A. Cabrera, A. Simon, M. Prado. Optimal synthesis of mechanisms with genetic algorithms[J]. Mechanism and Machine Theory,2002(37):1165-1177. [6] 趙升噸.高速壓力機的現狀及其發展趨勢[J].鍛壓裝備與制造技術,2005(01):17-25. [7] 林偉慶,李振石,李建平,等.基于遺傳算法的多連桿壓力機運動優化方法[J].鍛壓技術, 2011,36(05):81-84. [8] 孫昕煜,孫宇,彭斌彬.多連桿壓力機優化設計[J].機械制造與自動,2015,44(02):29-32. [9] 李初曄,孫彩霞,鄭會恩.基于ANSYS的多連桿機構性能優化[J].鍛壓技術,2011.36(06):80-83. [10]余發國,王園.一種八連桿機械壓力機連桿的優化設計[J].鍛壓技術,2013.38(05):138-141. [11]王曉麗,周天源.壓力機八桿內滑塊機構的優化設計[J].農業機械學報,2007,38(12):232-234. [12]范云霄.牟波.管聰聰.基于ADAMS的八連桿壓力機的優化設計[J].機械制造與自動化,2014,43(02):105-107. [13]雷德明,嚴新平.多目標智能優化算法及其應用[M].北京:科學出版社,2009. [14]白云嬌,王開榮.一種關于目標罰參數的精確罰函數法[J].數值計算與計算機應用,2014,35(01):35-44. [15]公茂果,焦李成,楊咚咚,等.進化多目標優化算法研究[J].軟件學報,2009,20(02):271-289. [16]夏鏈,肖傳清,韓江,等.基于Adams的多連桿機械式壓力機動力學分析[J].重型機械,2011,(06):67-70. [17]何德譽.曲柄壓力機[M].北京:機械工業出版社,1981. [18]何予鵬,趙升噸,楊輝,等.機械壓力機低速鍛沖機構的遺傳算法優化設計[J].西安交通大學學報,2005,39(05):490-493. [19]鄭文緯,吳克堅.機械原理[M].北京高等教育出版社,2012. Eight-links mechanical press linkages design based on NSGA-II algorithm YUAN Liang-zhao1,ZHAI Hua1,2,ZHANG Lan-jun3,Gao Guang-quan3, WANG Yu-shan3 (1.Institute of Industry and Equipment Technology,Hefei University of Technology,Hefei 230009, China;2.College of Mechanical and Automotive Engineering,Hefei University of Technology,Hefei 230009, China;3.Hefei Metal-forming Machine Tool Co.,Ltd.,Hefei 230601, China) According to the precise design requirement of eight-linkages mechanical press, a multi-objective function of minimum of the stroke design error and the working stroke drawing velocity fluctuation was established, which dynamics characteristics of mechanism as the constraint conditions. The NSGA-II algorithm was used to optimize the mathematical model which contains 12 variables,and ensured that the minimum stroke design error was the first additional criterion, and the final system parameters are determined in the Pareto optimal solution. Optimization example shows that this method can provide reference for the rapid design of eight- linkages mechanical press. mechanical press; eight- linkages; NSGA-II; optimization 2016-10-15; 2016-11-09 2013年度安徽省合蕪蚌自主創新試驗區專項資助(項目號20130205) 袁良照(1993-),男,合肥工業大學碩士研究生。 翟華(1973-),男,博士,教授,合肥工業大學工業與裝備技術研究院。 TG385 A 1001-196X(2017)02-0054-06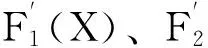
4 仿真實驗

5 結論

