具有執行器飽和切換系統的控制
景 麗, 董秋陽
(沈陽師范大學 數學與系統科學學院, 沈陽 110034)
?
具有執行器飽和切換系統的控制
景 麗, 董秋陽
(沈陽師范大學 數學與系統科學學院, 沈陽 110034)
主要研究了一類具有執行器飽和的切換系統的控制問題,探究當切換系統中執行器出現飽和時,系統要達到漸近穩定需要滿足的充分條件,并證明所得結論。首先,針對執行器飽和系統,處理飽和項至關重要。利用扇形區域法的思想,成功解決飽和項的處理問題。其次,為系統選擇適當的李雅普諾夫函數,進而研究獲得執行器飽和切換系統的的漸近穩定判據。然后,為使求解更加方便快捷,對獲得系統漸近穩定的充分條件做變形處理,將其轉換成線性矩陣不等式形式。最后,進行吸引域大小的估計,結合相應的仿真算例,證明了研究成果是有效可行的。
切換系統; 執行器飽和; Lyapunov理論; 線性矩陣不等式
0 引 言
限制和約束廣泛存在于實際生產生活中,其中飽和執行器會很大程度上對系統整體性能造成破壞,更嚴重的將引起系統的不穩定。一些離散或連續的子系統,在相應切換規則的嚴格控制下,會巧妙組合成復雜的切換系統。本文針對具有執行器飽和切換系統的控制問題進行研究是十分必要的。對于飽和系統的研究成果十分豐富,如文獻[1-5]。文獻[6]是飽和控制系統研究中的重要成果,由Sontag等人在1990年完成,指出當飽和線性系統的輸入有界漸近零可控時,系統將達到全局穩定,此時將有光滑非線性控制器出現在系統之中。文獻[7-10]以執行器飽和線性系統研究成果為基礎,進一步探究飽和對切換系統的影響,用凸優化問題解決吸引域大小的估計。
本文主要研究執行器飽和切換系統的控制問題,巧妙地將執行器飽和與切換系統相結合,在飽和項的處理,控制器的設計方面均有良好的突破。
1 問題描述
考慮執行器飽和切換系統:
(1)
其中:x∈Rn為系統狀態向量;u∈Rm為控制輸入向量;Ai,Bi為適當維數的常矩陣;i=1,2,…,N。飽和非線性函數sat(·)定義如下:
sat(u)=[sat(u1),sat(u2),…,sat(um)]T
其中δ>0。
引入狀態反饋控制律:
(2)

本文探究當切換系統的執行器出現飽和現象時,系統想要達到穩定所需滿足的條件。主要涉及到相應狀態反饋控制器的設計以及系統最大吸引域的估計。
下面給出進行本文研究需要的相關定義、定理等。
定義1(橢球集合)[11]P>0,P∈Rn×n,ρ>0為標量,定義橢球體為
定義3(吸引域)[11]假設系統的初始點和解分別為x(0)=x0∈Rn,φ(t,x0),那么系統的吸引域是:
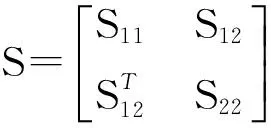
1) S<0;
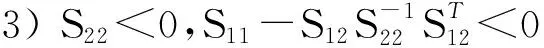
引理2[12]給定矩陣A、L、E、F, 若FTF≤I,則有以下不等式成立
其中:α>0,F>0。
2 執行器飽和切換系統的控制及吸引域估計
2.1 執行器飽和切換系統的控制
定理1 對于執行器飽和切換系統(1),如果在控制器(2)作用下存在滿足如下不等式的矩陣Qi∈Rm×n,i=1,2,…,N和正定矩陣Ni>0,那么系統(1)在原點局部漸近穩定。
證明 對于式(2),由范數的三角不等式性質可得
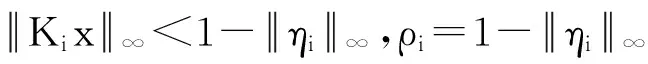
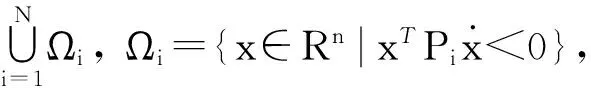
[(Ai+BiKi)x+Biηisat(x)]TPix+xTPi[(Ai+BiKi)x+Biηisat(x)]=
令
(3)
(4)
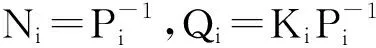

由引理2得到
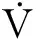
2.2 吸引域估計
根據定理1給出的系統穩定條件,借助橢球體參考集進行吸引域的估計,進而獲得最大的吸引域。
需要解決如下凸優化問題:
(5)
(6)
(7)
其中式(5)是系統穩定的條件,式(6)將吸引域限制在橢球體內,式(7)表示橢球包含在多面體內。
式(6)等價于
(8)
式(7)等價于
(9)
于是優化問題可以轉化為
(10)

3 仿真算例
對于執行器飽和切換系統(1)
令i=1,2, 取系統(1)的2個子系統:
設系統狀態矩陣、輸入矩陣為
另外設
利用LMI工具箱求得式(10)的解,如下:
γ1=18.636 0, γ2=6.336 3,
系統初始狀態選為:x=(2,0.9)T, 系統(1)在狀態反饋控制器(2)的作用下漸近穩定,如圖1、圖2所示。
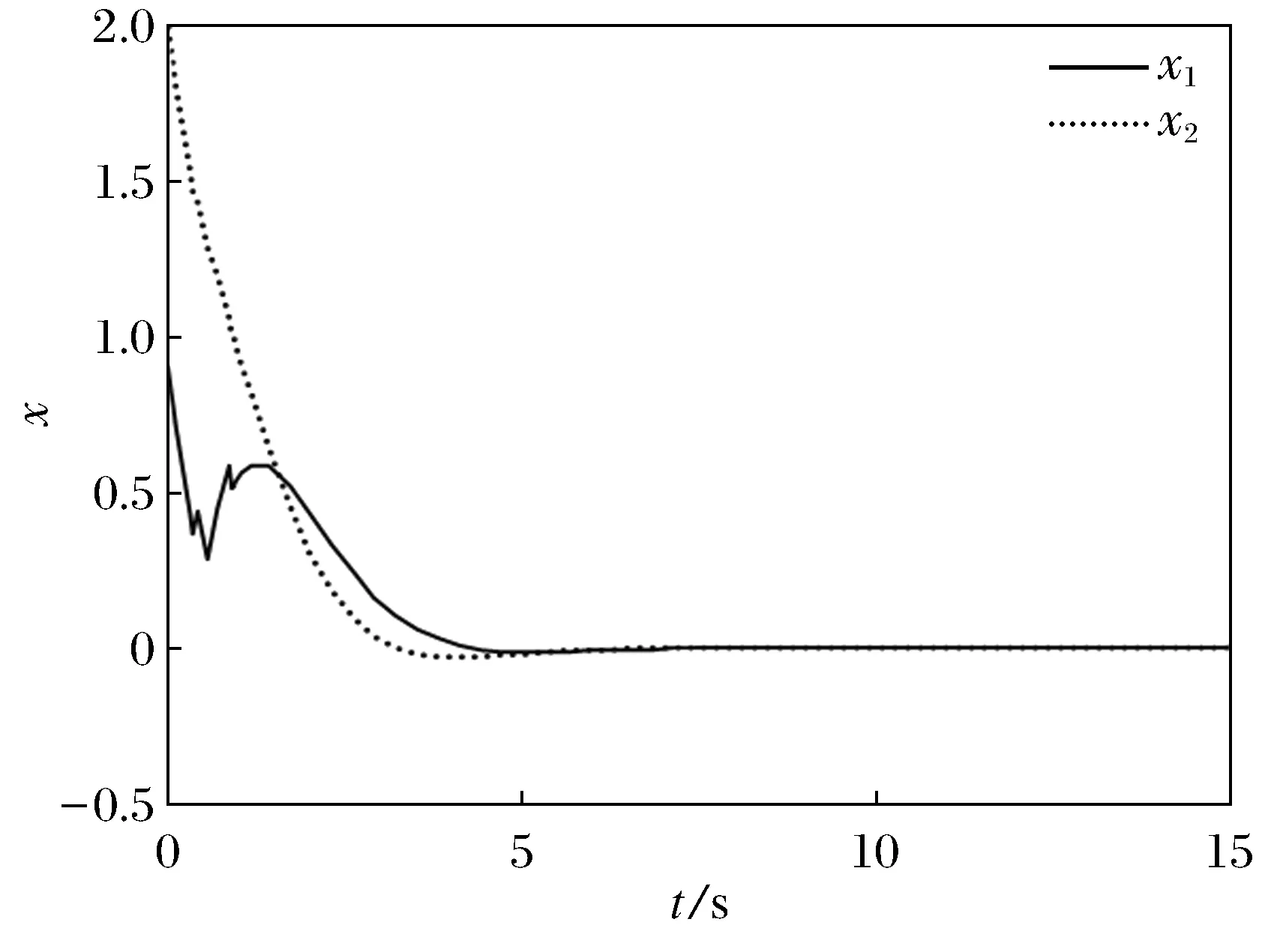
圖1 系統狀態軌跡
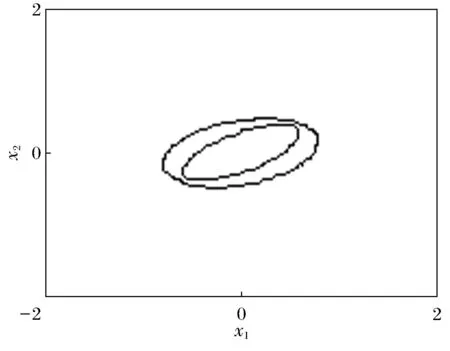
圖2 系統吸引域圖
4 結 論
本文所研究的是復雜的切換系統,并且系統包含的執行器飽和,這加大了系統研究的難度。執行器飽和的飽和項處理問題運用扇形區域法思想解決。基于李雅普諾夫穩定性理論,并利用線性矩陣不等式知識,給出系統實現漸近穩定需要滿足的條件。選用橢球體為參考集,進一步估計吸引域的大小。
[ 1 ]HOU L, ANTHONY N. Asymptotic stability of systems with saturation constraints[J]. IEEE Transaction on Automatic Control, 1998,43(8):1148-1154.
[ 2 ]BLANCHINI F. Control of linear systems with regulation and input constraints[J]. Communications and Control Engineering, 2000,19(11):46-53.
[ 3 ]BERNSTEIN D S, MICHEL A N. A chronological bibliography on saturating actuators[J]. International Journal of Robust and Nonlinear Control, 1995,5(5):374-381.
[ 4 ]SABERI A, LIN Z, TEEL A R. Control of linear systems with saturating actuators[J]. IEEE Transaction on Automatic Control, 1996,41(3):368-378.
[ 5 ]俞國軍. 帶飽和執行器的線性系統的魯棒控制研究[D]. 杭州: 浙江工業大學, 2003.
[ 6 ]SONTAG E D, SUSSMANN H J. Nonlinear output feedback design for linear systems with saturating controls[C]∥IEEE Control Systems Soc. Proceedings of the Conference on Decision and Control, Honolulu HI USA, 1990:3414-3416.
[ 7 ]張新權. 幾類具有執行器飽和的切換系統的分析與綜合[D]. 沈陽: 東北大學, 2011.
[ 8 ]李曉銀. 具有執行器飽和的非線性切換系統的優化與控制研究[D]. 阜新: 遼寧工程技術大學, 2012.
[ 9 ]YUAN C Z, WU F. Switching control of linear systems subject to asymmetric actuator saturation[J]. International Journal of Control, 2015,881:424-451.
[10]DUAN C, WU F. New results on switched linear systems with actuator saturation[J]. International Journal of Systems Science, 2016,475:276-289.
[11]周麗明. 飽和控制系統理論及應用研究[D]. 哈爾濱: 哈爾濱工業大學, 2009.
[12]俞立. 魯棒控制線性矩陣不等式處理方法[M]. 北京: 清華大學出版社, 2002.
[13]ZUO Z Q, Wang Y J, On enlarging the domain of attraction for linear systems subject to actuator saturation[J]. International Journal of General Systems, 2008,37(2):239-248.
[14]趙克友,魏愛榮. 執行器飽和線性系統的鎮定性[C]. 2005中國控制與決策學術年會, 沈陽2005:102-104.
[15]馬東星. 飽和系統的穩定性分析與抗飽和控制[D]. 杭州: 浙江大學, 2006.
[16]呂亮. 具有執行器飽和的控制系統分析與設計[D]. 上海: 上海交通大學, 2010.
[17]沈凡杰. 具有飽和執行器系統的控制方法研究[D]. 沈陽: 沈陽師范大學, 2016.
Control of switched systems with actuator saturation
JING Li1, DONG Qiuyang2
(College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)
In this paper, we study a class of switched systems with actuator saturation. We mainly explore the stability criterion of the system when actuator saturation exists, and prove the conclusion. Firstly, how to dispose saturation is very important. We dispose saturation by using the sector region method. Secondly, according to the Lyapunov theory, the paper gets the stability criterion. Thirdly, the paper turns the criterion into the inequality in order to solve the problem by LMI tools in Matlab. Finally, the paper estimates the attraction domain of the system. It also provides a numerical example to demonstrate that the conclusion in this paper is effective and feasible.
switched system; actuator saturation; Lyapunov theorem; linear matrix inequality
1673-5862(2017)02-0151-05
2017-05-10。
遼寧省教育廳科學研究一般項目(L2014435)。
景 麗(1967-),女,遼寧沈陽人,沈陽師范大學副教授,博士。
O436
A
10.3969/ j.issn.1673-5862.2017.02.005

