τ函數型Caristi不動點定理
徐厚生, 孫宇佳
(1. 沈陽建筑大學 理學院, 沈陽 110168; 2. 東北大學 理學院, 沈陽 110819)
?
τ函數型Caristi不動點定理
徐厚生1, 孫宇佳2
(1. 沈陽建筑大學 理學院, 沈陽 110168; 2. 東北大學 理學院, 沈陽 110819)
Caristi不動點定理是非線性分析中一個非常重要的結論,曾被評價很可能成為非線性泛函分析進一步發展的強有力的工具。這個結果不僅是Banach壓縮原理的推廣,而且在不動點理論和變分方法中產生了深遠的影響。事實上,Caristi不動點定理等價于Ekeland變分原理。近40年來,Caristi不動點定理在多方面得到討論與推廣,條件的減弱和形式更加一般化使得應用的范圍越來越廣,特別是減弱條件中關于度量函數的要求更具有重要的意義。應用半序集及極小元定理,在完備度量空間中得到τ函數型Caristi不動點定理需要與下方有界下半連續泛函相關的不等式條件。推廣了已有文獻中的結果,將原來不等式條件中的度量函數d減弱為τ函數,不等式右端具有上半連續函數的形式,推論中包含了多值映射的結果。
不動點;τ函數; 半序集; 極小元
0 引 言
Caristi在文獻[1]中給出了一個非常重要的定理,這個結果不僅是Banach壓縮原理的推廣,而且在不動點理論和變分方法中產生了深遠的影響。
定理1[1](Caristi不動點定理)設(X,d)是完備的度量空間,T:X→X,φ是X上的下方有界下半連續的泛函。如果對任意的x∈X,滿足

則T在X上存在不動點。
近40年來,Caristi不動點定理在多方面得到討論與推廣,見文獻[2-14]等。文獻[14]給出了幾個形式比較一般的Caristi型不動點定理,其中最核心的是下面的定理2.
定義1[14]設γ:[0,+∞)→[0,+∞)是次可加的函數, 即γ(t+s)≤γ(t)+γ(s),?t, s≥0,并且γ是連續單調遞增的, 同時滿足γ-1({0})={0}。所有這樣的函數的集合記做Γ。
例如函數γ(t)=tp, t≥0(0 定義3[14]設函數F:R→R,F(0)=0,F-1[0,+∞)?[0,+∞),并且當t≥0時,F(t)是單調遞增函數,且F(t)是一個上半連續函數,另外當t, s≥0時,F(t)+F(s)≤F(t+s)。所有這樣的函數的集合記作I。 例如函數 其中t0>1且p≥1。如果令F(t)=t, ? t∈R, 那么F∈I是平凡的。 定理2[14]設(X,d)是完備的度量空間,T:X→X,φ是X上的下方有界下半連續的泛函。如果存在η∈Α,F∈I, 使得?x∈X, 滿足 (1) 則T存在不動點。 定義4[15]設(X,d)是度量空間,函數ω:X×X→[0,+∞)稱為X上的τ函數, 如果滿足下列條件: (ω1) (三角不等式) ω(x,z)≤ω(x,y)+ω(y,z) ?x,y,z∈X; (ω3) ?x,y,z∈X,若ω(x,y)=0, ω(x,z)=0, 則y=z; 顯然(X,d)中的度量函數d就是X上的τ函數。本文將條件(1)中的度量函數d減弱為τ函數, 從而推廣了文獻[14]中的一系列結果。 定理3 設(X,d)是完備的度量空間,T:X→X,φ是X上的一個下方有界下半連續泛函。如果存在一個τ函數p,η∈A,F∈I滿足 (2) 則T存在不動點。 證明 1) ?x, y∈X, 定義 (3) 設Xδ={x∈X|φ(x)≤φ0+δ},顯然,Xδ非空。根據引理2以及φ是下半連續泛函,知Xδ是一個閉集。由于Xδ是X的子集,故Xδ也是完備的,則(Xδ,d)是完備度量空間。 ?x,y∈Xδ,有 (4) 如果x≤sy,則根據0≤η(p(y,x))≤F(φ(y)-φ(x)),且F-1[0,∞)∈[0,∞), 可得 根據式(4),有0≤φ(y)-φ(x)≤δ,且 (5) 2) 在Xδ中, 定義 (6) 證明≤為一個擬序。 1) 反身性:?x∈Xδ,若x=x,則根據(2.5)知 x≤x,即x=x?x≤x; 2) 傳遞性:若x≤y, y≤z; ⅰ) 根據(6)知第1種情況 再根據γ的單增性以及次可加性有 再由式(6)以及函數F的性質有 綜上 則有x≤z。 ⅱ) 由式(6)知第2種情況 由于y=z,故將γ(p(y,x))≤F(φ(y)-φ(x))中的y用z替換,即可得到 則有x≤z. ⅲ) 由式(6)知第3種情況 由于x=y,故將γ(p(z,y))≤F(φ(y)-φ(x))中的y用z替換,即可得到 則有x≤z。 ⅳ) 由式(6)知第4種情況 x=y, y=z 由x=y, y=z知x=z, 則有x≤z。 綜上, ≤為一個擬序。 3) 這一部分主要證明(Xδ,≤)存在極小元。 ① 由于(Xδ,d)是完備的度量空間, 故(Xδ,≤)是≤完備的; ② 設{xn}是(Xδ,≤)中的下降點列, 則有 (7) 再根據F-1[0,∞)∈[0,∞), 有 因此, {φ(xn)}是一個實數列, 下降且有下界。 再由式(7)知 因此 又γ-1(0)={0}, 且γ連續, 故 又d(x,y)=d(y,x), 故有 即{xn}是漸近的, 即≤是正則的。 ③ 設{xn}是Xδ中收斂到x的下降點列。 由于xn→x,n→∞, φ是一個下方有界下半連續泛函, 故有 對于任意的n,取m>n,當m→∞時,有xm≤xn,由≤的定義有 ?ε>0, 有 令F(φ(xn)-φ(x))+ε=K, 則K>0。則 又γ-1(0)={0}, γ是增的, 則有 則 則由τ函數定義中的(τ4), 有p(xn,x)≤M。 因此 當ε→0時, 有 則有?n, 有x≤xn, 即≤是下閉的。 則根據極小元引理, 知(Xδ,d,≤)中存在極小元。不妨設x*為(Xδ,d,≤)中的極小元。 4) 這部分證明x*也是(X,≤s)中的極小元, 即若x∈X, 且有x≤sx*, 則x=x*。 設x∈X, x≤sx*, 由≤s的定義知 (8) 根據(8)以及F-1[0,∞)∈[0,∞), 知 (9) 由于x*∈Xδ, 根據φ0的定義和Xδ的定義, 有 (10) 由式(9)、式(10)知,φ0≤φ(x)≤φ0+δ, 則有x∈Xδ, 且0≤φ(x*)-φ(x)≤δ。 根據δ的選擇, 有 即x≤x*。由于x*為(Xδ,d,≤)中的極小元, 則有x=x*, 即x*也是(X,≤s)中的極小元。 由于x*是(X,≤s)中的極小元, 又根據 以及≤s的定義, 知Tx*≤sx*, 則有Tx*=x*, 即T存在不動點。 推論1 (X,d)是完備的度量空間, 設T:X→2X{?},φ是X上的一個下方有界下半連續泛函。如果存在一個τ函數p,η∈A,F∈I滿足對于任意的x∈X, 存在y∈Tx滿足 則T存在不動點, 即存在x*∈X使得 x*∈Tx*。 定理4 設(X,d)是完備的度量空間,T:X→X,φ是X上的一個下方有界下半連續泛函。假設Φ是X上的一個正函數, 并且存在δ>0使得 如果存在η∈Α, F∈I, 以及一個τ函數p滿足 則T有不動點。 證明 由于Φ(x)>0, 則根據η的定義可得F(φ(x)-φ(Tx))≥0, 再由F的定義知φ(x)≥φ(Tx)。 顯然, 由φ是下半連續的知Xδ是閉集, 且Xδ≠?。因此(Xδ,d)是完備的度量空間。 ?x∈Xδ, 有φ(Tx)≤φ(x)≤φ0+δ, 即Tx∈Xδ, 即T:Xδ→Xδ。由于 知η(p(x,Tx))≤αF(φ(x)-φ(Tx)),?x∈Xδ。 顯然, αF∈I.,因此由定理3知, 存在x0∈Xδ∈X滿足Tx0=x0, 即T有不動點. 定理5 設(X,d)是完備的度量空間,T:X→X,φ:[0,+∞)→(0,+∞)是右上半連續函數,φ是X上的下方有界下半連續的泛函, 如果存在η∈Α,F∈I,以及一個τ函數p使得?x∈X, 滿足條件 則T存在不動點。 定義Φ(x)=max{φ(φ(x)), φ(φ(Tx))}, ?x∈X, 則Φ:X→(0,+∞)。 由于Φ(x)>0, 那么F(φ(x)-φ(Tx))≥0, 從而φ(Tx)≤φ(x)。因此?x∈X, φ(Tx)≤φ(x)。 因此由定理4, 則T存在不動點。 定理6 設(X,d)是完備的度量空間,T:X→X,φ:R→(0,+∞)是單調遞增函數,φ是X上的下方有界下半連續的泛函, 如果存在η∈Α,F∈I以及一個τ函數p, 使得?x∈X, 滿足條件 (11) 或 (12) 則T存在不動點。 證明 定義Φ(x)=φ(φ(x)), ?x∈X, 則Φ:X→(0,+∞)。那么 從而φ(Tx)≤φ(x)。故φ(φ(Tx))≤φ(φ(x)), ?x∈X。所以只要證明對于式(12)條件成立, 則對于條件(11)也成立。 那么根據定理4, 該結論得證。 本文應用半序方法及極小元引理,通過與下方有界下半連續泛函相關的不等式條件,在完備度量空間中得到了函數型Caristi不動點定理。本文的結論是已有文獻中結果的推廣,主要是將原來不等式條件中的度量函數減弱為函數,同時不等式右端具有上半連續函數的形式。另外推論中包含了多值映射的相應結果。 [ 1 ]CARISTIJ.Fixedpointtheoremsformappingssatisfyinginwardnessconditions[J].TransAmerMathSoc, 1976,215:241-251. [ 2 ]BAE J S. Fixed point theorems for weakly contractive multivalued maps[J]. J Math Anal Appl, 2003,284(2):690-697. [ 3 ]DOWNING D, KIRK W A. A generalization of Caristi’s theorem with applications to nonlinear mapping theory[J]. Pacific J Math, 1977,69(2):339-346. [ 4 ]FENG Y Q, LIU S Y. Fixed point theorems for multi-valued contractive mappings and multi-valued Caristi type mapping[J]. J Math Anal Appl, 2006,317(1):103-112. [ 5 ]JACHYMSKI J R. Caristi’s fixed point theorem and selections of set-valued contractions[J]. J Math Anal Appl, 1998,227(1):55-67. [ 6 ]KADA O, SUZUKI T, TAKAHASHI W. Nonconvex minimization theorems and fixed point theorems in complete metric spaces[J]. Math Japon, 1996,44(2):381-391. [ 7 ]KHAMSI M A. Remarks on Caristi’s fixed Point theorem[J]. Nonlinear Anal, 2009,71(1/2):227-231. [ 8 ]KIRK W A. Caristi’s fixed point theorem and metric convexity[J]. Colloq Math, 1976,36(1):81-86. [ 9 ]SHIOJI N, SUZUKI T, TAKAHASHI W. Contractive mappings, Kannan mappings and metric completeness[J]. Proc Amer Math Soc, 1998,126(10):3117-3124. [10]SUZUKI T. Generalized Caristi’s fixed point theorems by Bae and Others[J]. J Math Anal Appl, 2005,302(2):502-508. [11]SUZUKI T. Generalized distance and existence theorems in complete metric spaces[J]. J Math Anal Appl, 2001,253(2):440-458. [12]SUZUKI T. Several fixed point theorems in complete metric spaces[J]. Yokohama Math J, 1997,44(1):61-72. [13]SUZUKI T, TAKAHASHI W. Fixed point theorems and characterizations of metric completeness[J]. Topol Methods Nonlinear Anal, 1996,8(2):371-382. [14]ZHANG G W, JIANG D. On the fixed point theorems of caristi type[J]. Fixed Point Theory, 2013,14(2):523-530. [15]LIN L J, DU W S. Ekeland’s variational principle, minimax theorems and existence of nonconvex equilibria in complete metric spaces[J]. J Math Anal Appl, 2006,323(1):360-370. [16]宋叔尼,張國偉. 變分方法的理論及應用[M]. 北京: 科學出版社, 2012. [17]HAMEL A. Variational principles on uniform spaces[D]. Halle:Habilitation Thesis, 2005. On the fixed point theorems of Caristi’s type aboutτfunction XU Housheng1, SUN Yujia2 (1. School of Science, Shenyang Jianzhu University, Shenyang 110168, China; 2. School of Science, Northeastern University, Shenyang 110819, China) Caristi fixed point theorem is a very important conclusion in nonlinear analysis, and it was remarked that it is likely to be a powerful tool in further development of nonlinear functional analysis. This result is not only a generalization of Banach contraction principle, but also has a profound influence on the fixed point theory and variational methods. In fact, Caristi fixed point theorem is equivalent to Ekeland variational principle. In the past forty years, Caristi fixed point theorem has been discussed and generalized in many aspects. The weakening of the conditions and the more general forms make the application more and more widely, it is especially more important to reduce the requirement of metric function in the condition. By using partially ordered set and minimal element theorem, Caristi fixed point theorem ofτfunction’s type is obtained in complete metric spaces under the inequality condition concerning lower bounded and lower semi-continuous functional. Some results in references are extended, the metric functiondin original inequality condition is reduced toτfunction and the right side of the inequality has the form of upper semi-continuous function. The result of multi valued mapping is included in the corollary. fixed point;τfunction; ordered set; minimal element 1673-5862(2017)02-0145-06 2017-02-01。 遼寧省科技廳自然科學基金資助項目(20170540769)。 徐厚生(1972-),男,山東臨沂人,沈陽建筑大學副教授,碩士。 O177.91 A 10.3969/ j.issn.1673-5862.2017.02.004

1 主要結論









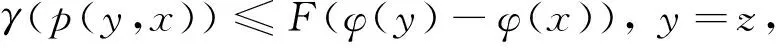




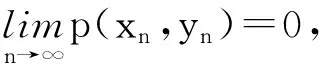
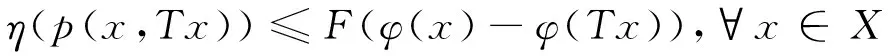
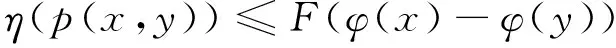

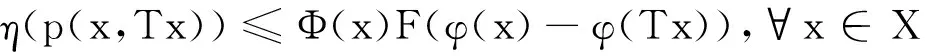

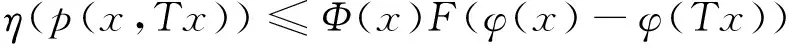
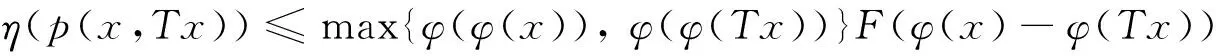


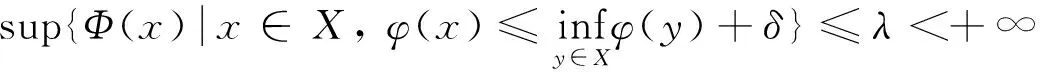

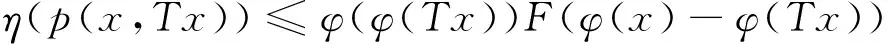
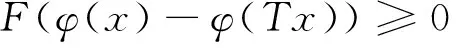

2 結 語

