慣性質量衰減的引力搜索算法

錢偉懿, 張麗佳

(渤海大學 數理學院, 遼寧 錦州 121013)

?

運籌學與控制論

慣性質量衰減的引力搜索算法

錢偉懿, 張麗佳

(渤海大學 數理學院, 遼寧 錦州 121013)

針對引力搜索算法易陷入局部最優的缺點,提出一種慣性質量衰減的引力搜索算法。 該算法認為粒子的慣性質量有一定衰減,把粒子慣性質量的衰減率看成一個模糊變量,用其隸屬度函數定義慣性質量的衰減率,把衰減率與粒子慣性質量乘積作為粒子的慣性質量,從而提高算法的開發能力。另外,為了提高算法的探索能力,給出一個新的變異算子。最后,把所提出算法應用到經典測試函數中,并與引力搜索算法及其他改進的引力搜索算法比較,數值結果表明所給出的算法能夠提高求解精度和收斂速度。

引力搜索算法; 隸屬度函數; 變異算子; 全局優化

在過去幾十年中,研究人員從自然現象中得到啟發,提出了許多啟發式優化算法。例如,遺傳算法[1]、蟻群優化算法[2]、粒子群優化算法[3-4]、模擬退火法[5]、人工蜂群算法[6]等。這些算法都是針對某些特定問題,目前尚沒有哪一種算法能夠成功地解決所有的優化問題。因此,探索新的算法十分必要。

引力搜索算法(Gravitational search algorithm, GSA)是一種新的啟發式優化算法,在2009年,首先被Esmat等人提出[7-8],其原理源于對萬有引力進行模擬產生的群體智能優化算法。目前引力搜索算法得到了廣泛應用,如流水線調度[9]、模糊聚類[10-11]、濾波器的建模[12], 引起許多學者的關注。

Sun等人基于引力搜索算法和遺傳算法提出了一種混合GSA算法[13]。曹茂俊等人[14]在引力搜索算法中融合量子計算提出了一種改進的引力搜索算法。Tsai等人提出了一種引力粒子群算法[15],該算法通過粒子群優化算法的速度更新公式和GSA加速度更新公式的結合提出一種新速度更新公式。張明等人把小生境技術引入到引力搜索算法中給出一種基于小生境技術的改進引力搜索算法[16]。徐遙等人對粒子的慣性質量附加一個權值,提出了基于權值的引力搜索算法[17]。隋永霞等人提出基于高斯變異的引力搜索算法[18]。王奇琪等人引入斥力,提出了基于斥力的引力搜索算法[19]。這些算法未對慣性質量進行研究,但隨著時間推移粒子的慣性質量有一定衰減,故本文給出慣性質量衰減系數,該系數看成模糊變量,用其隸屬度函數表示,質量衰減系數乘以慣性質量代替原慣性質量。為提高群體多樣性,引入一個新的變異算子,在每次迭代中,以概率p實行新變異算子的位置更新,以概率(1-p)實施引力搜索算法位置更新,從而有效平衡了算法的探索能力和開發能力, 數值結果驗證了算法的有效性。

1 引力搜索算法

GSA是基于牛頓的萬有引力定律和運動定律為基本原理的啟發式算法。在GSA中把可行域中的解看成一個粒子,粒子的慣性質量由粒子的適應值決定,適應值越好的粒子其質量越大,相反,適應值越差的粒子其質量越小。根據粒子的質量和粒子間的距離定義萬有引力,粒子在萬有引力作用下在可行域內朝著慣性質量大的粒子運動,即朝著較好的適應值運動,從而得到全局最優解。

在一個D維的搜索空間中,假設有N個粒子,定義第i個粒子的位置為

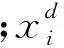
設第i個粒子在t時刻的質量為Mi(t),其表達式如下:

(1)

(2)

其中fiti(t)表示粒子i在t時刻的適應值,對于求最小值問題,best(t)和worst(t)定義如下:

(3)

(4)

根據萬有引力定律,在時刻t,粒子j對粒子i在d維上的作用力定義如下:

(5)

其中:Rij(t)為粒子i和粒子j之間的歐氏距離;ε是指非常小的常數;G(t)是t時刻的引力常數,定義如下:

(6)

其中:G0為一個初始值;α為一個常數;t為當前迭代數;tmax為最大迭代次數.

作用在第i個粒子在d維上的作用力定義如下:

(7)

其中randj是[0,1]之間的隨機數,kbest從N到1隨著時間t線性地減小,使得算法到最后在搜索空間中只有最好的解的那個粒子去作用于其他的粒子。

(8)

粒子i在第d維上的速度和位置更新如下:

(9)

(10)

其中randi是[0,1]之間的隨機變量。

2 質量衰減的GSA

隨著時間的推移,粒子的質量要有一定的衰減,本文把粒子質量衰減率看成一個模糊變量,模糊變量取決于他的隸屬度函數,本文基于高斯函數、鐘型函數、Sigmoid函數定義質量的衰減率,第i粒子在t時刻質量衰減率φi(t)定義如下:

若質量衰減率隸屬度函數基于高斯函數建立的,則

(11)

若質量衰減率隸屬度函數基于鐘型函數建立的,則

(12)

若質量衰減率隸屬度函數基于Sigmoid函數建立的,則

(13)

其中Pt表示t時刻最好位置,β為一參數,定義如下:

β=best(t)/log(1+t)

顯然t越大,β越小,從而質量衰減率越小,質量衰減越快。粒子i在t時刻衰減后的質量為

(14)

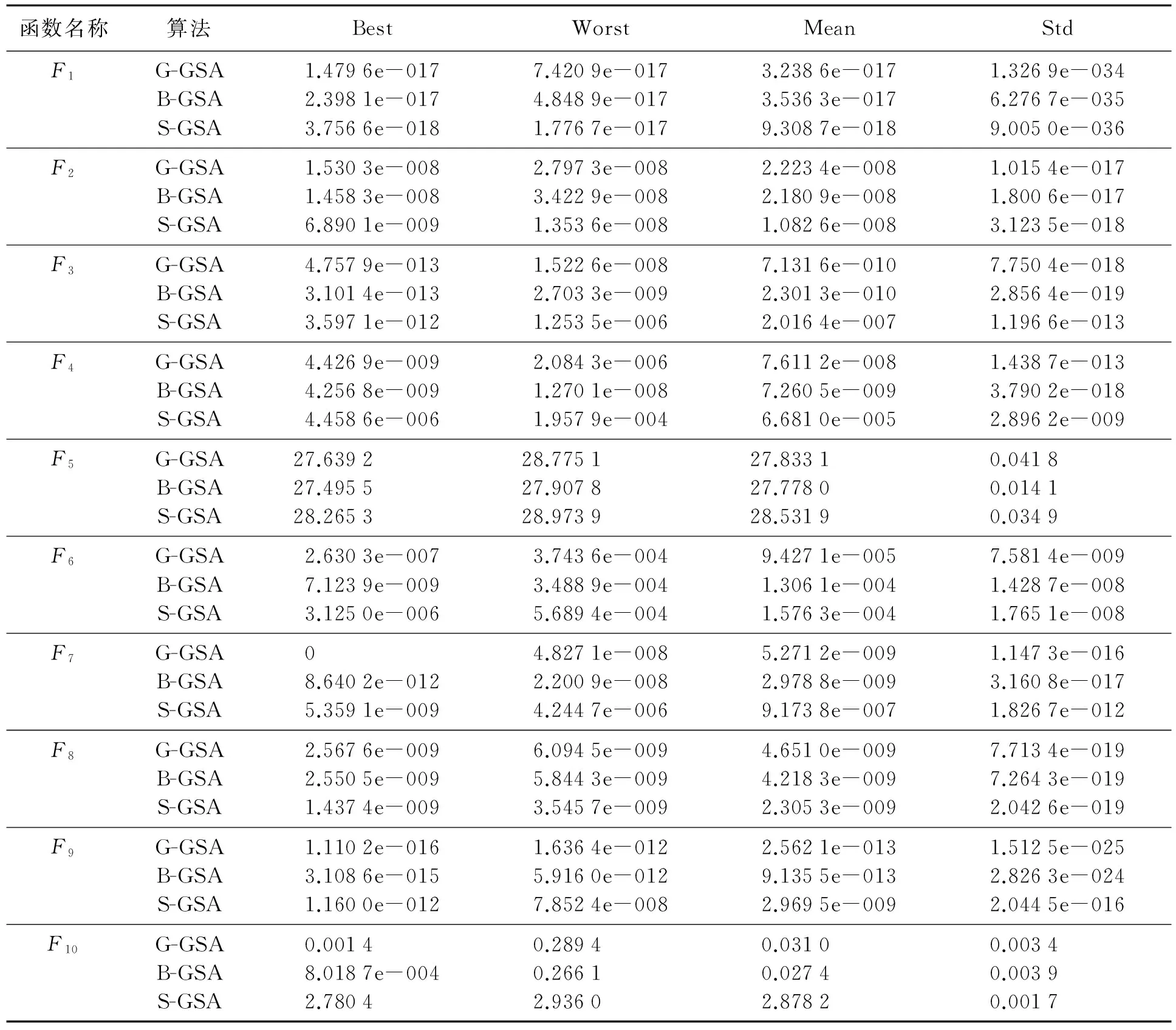
表1 測試函數

對于極小問題,粒子j的適應值越差(目標函數值大),其質量衰減率越小,從而衰減后質量越小,對其他粒子引力越小,相反,粒子j的適應值越好(目標函數值小),其質量衰減率越大,從而衰減后質量大,對其他粒子引力越大。該策略在算法后期可能導致陷入局部最優,為此給出一種新的變異算子

(15)

1) 設置算法中的參數,隨機初始化粒子的位置及速度,計算粒子的適應值,確定最好粒子;

2) 按式(1),式(2),式(3)和式(4)計算每個粒子的慣性質量;按式(6)計算引力常數;

3) 按式(11)或式(12)或式(13)計算慣性質量衰減率,按式(14)計算衰減后質量;

4) 按式(5)和式(7)計算每個粒子的引力;

5) 按式(8)計算加速度;

6) 按式(9)更新粒子的速度;

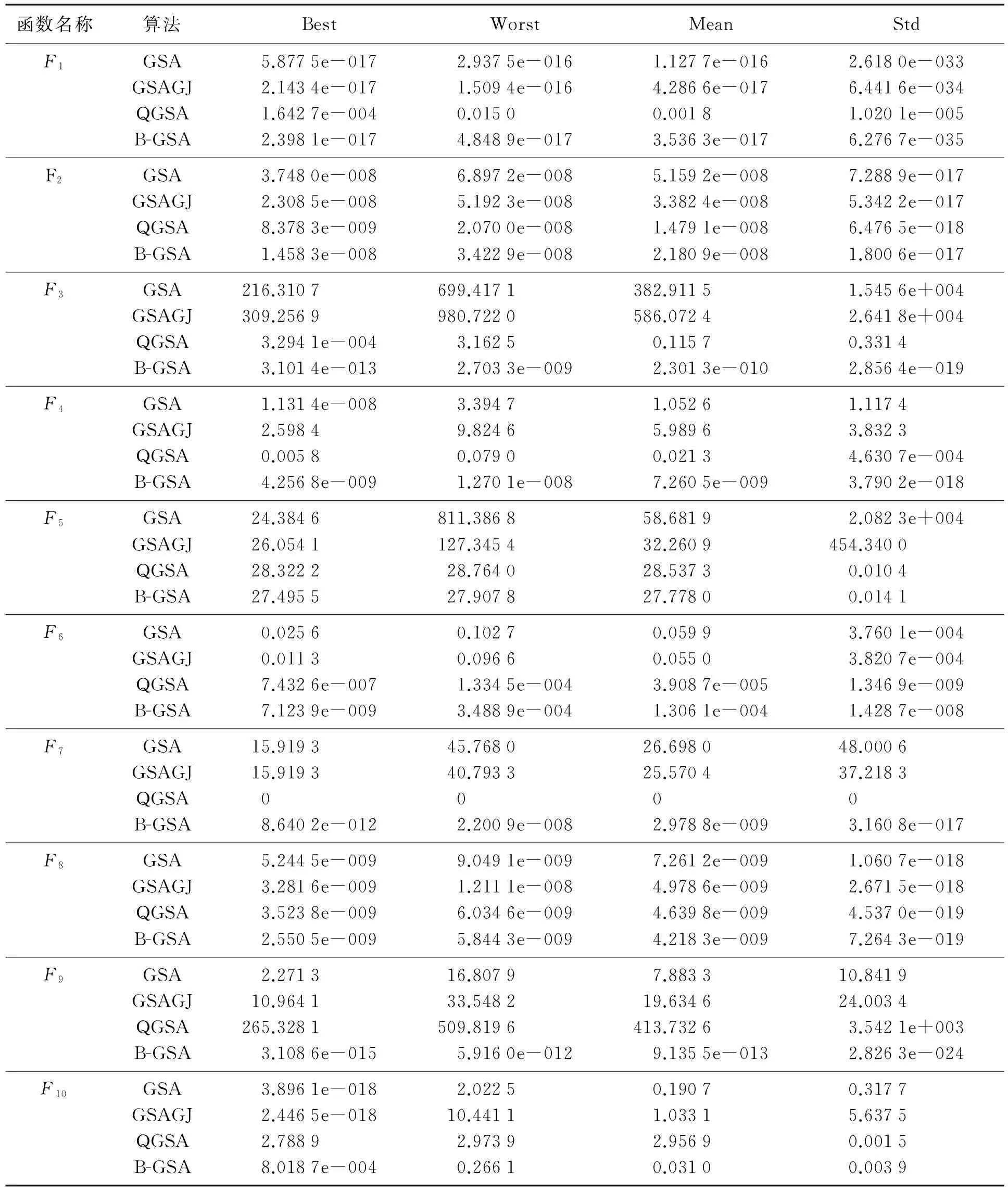
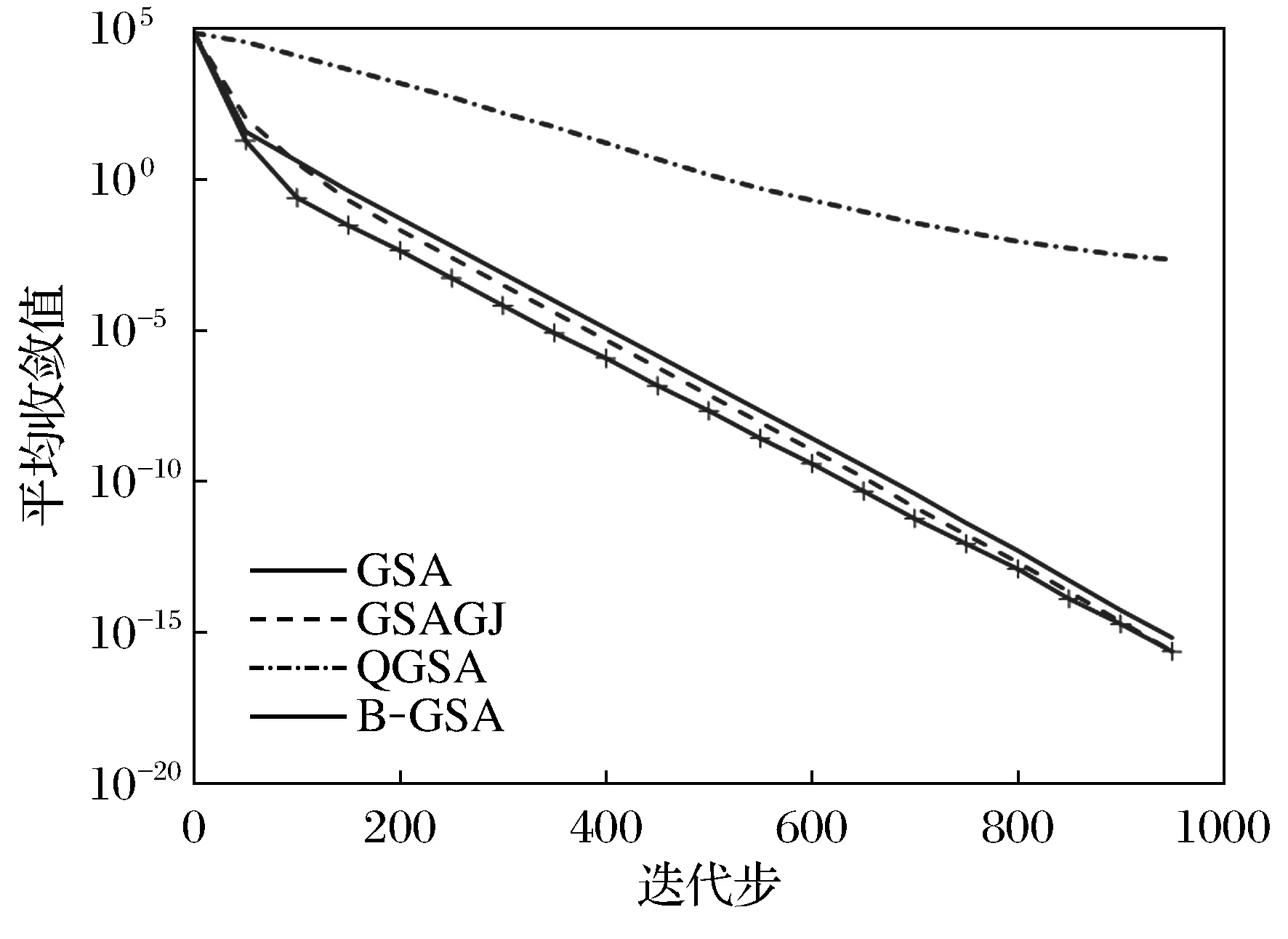
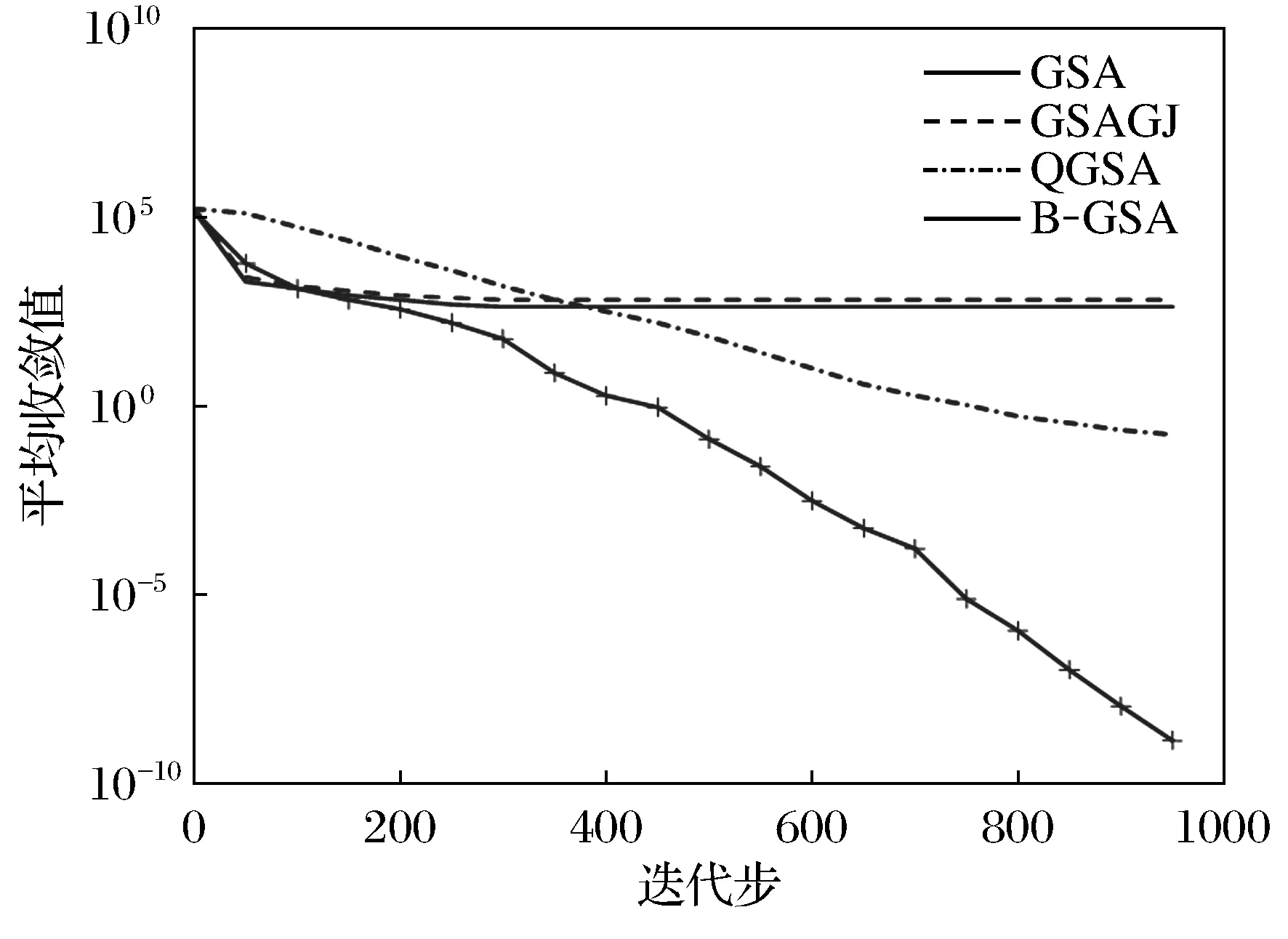
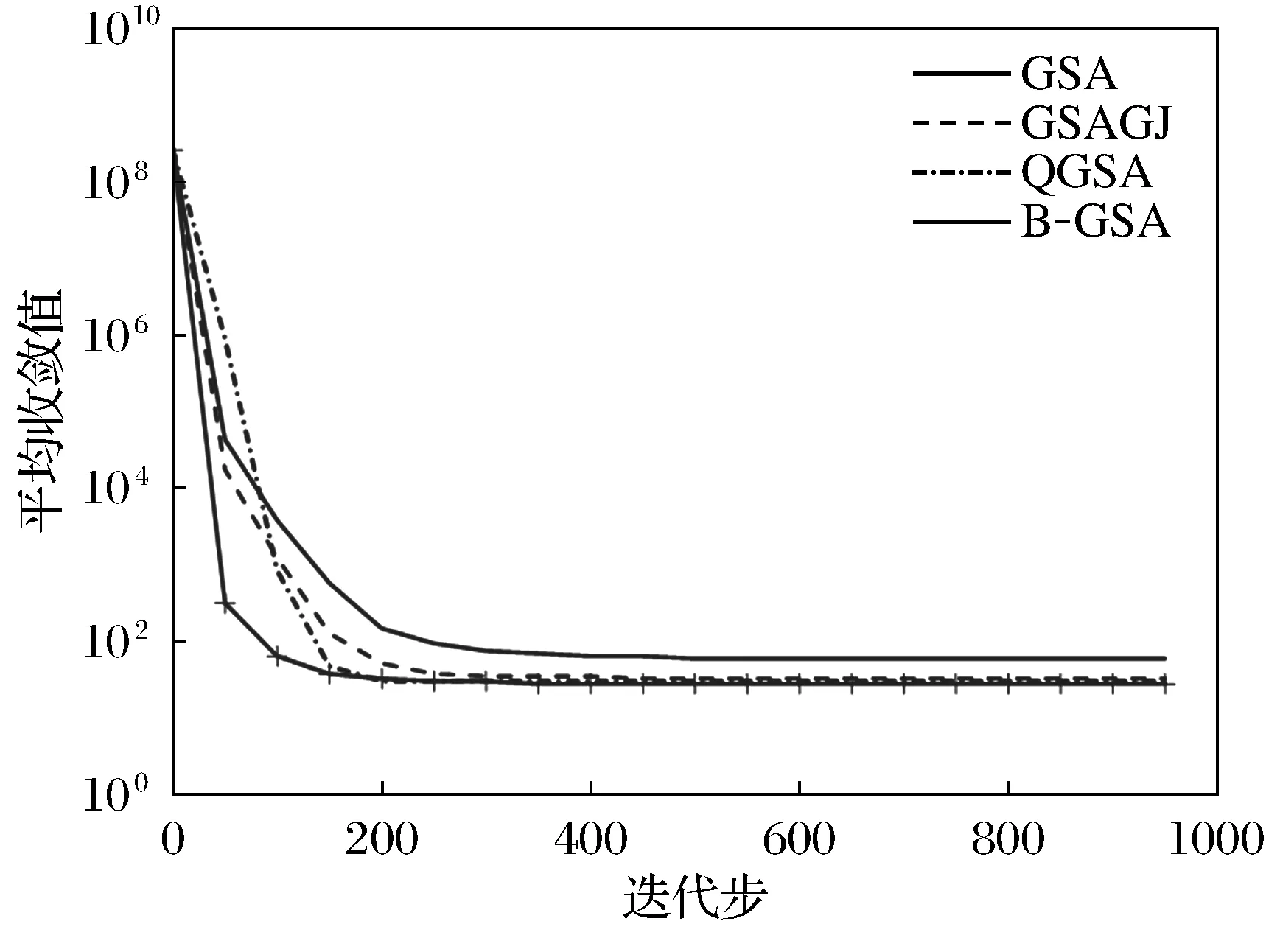
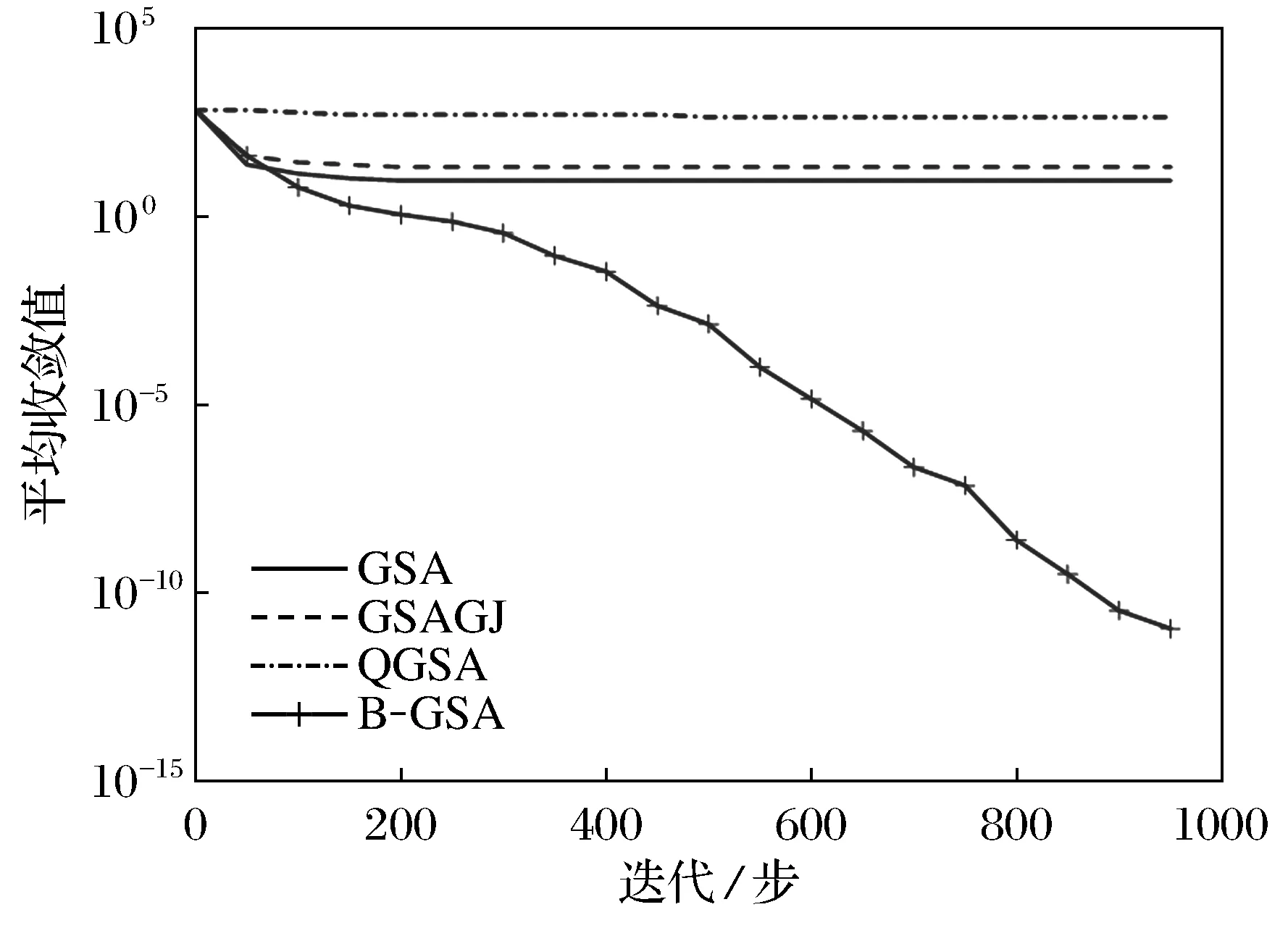
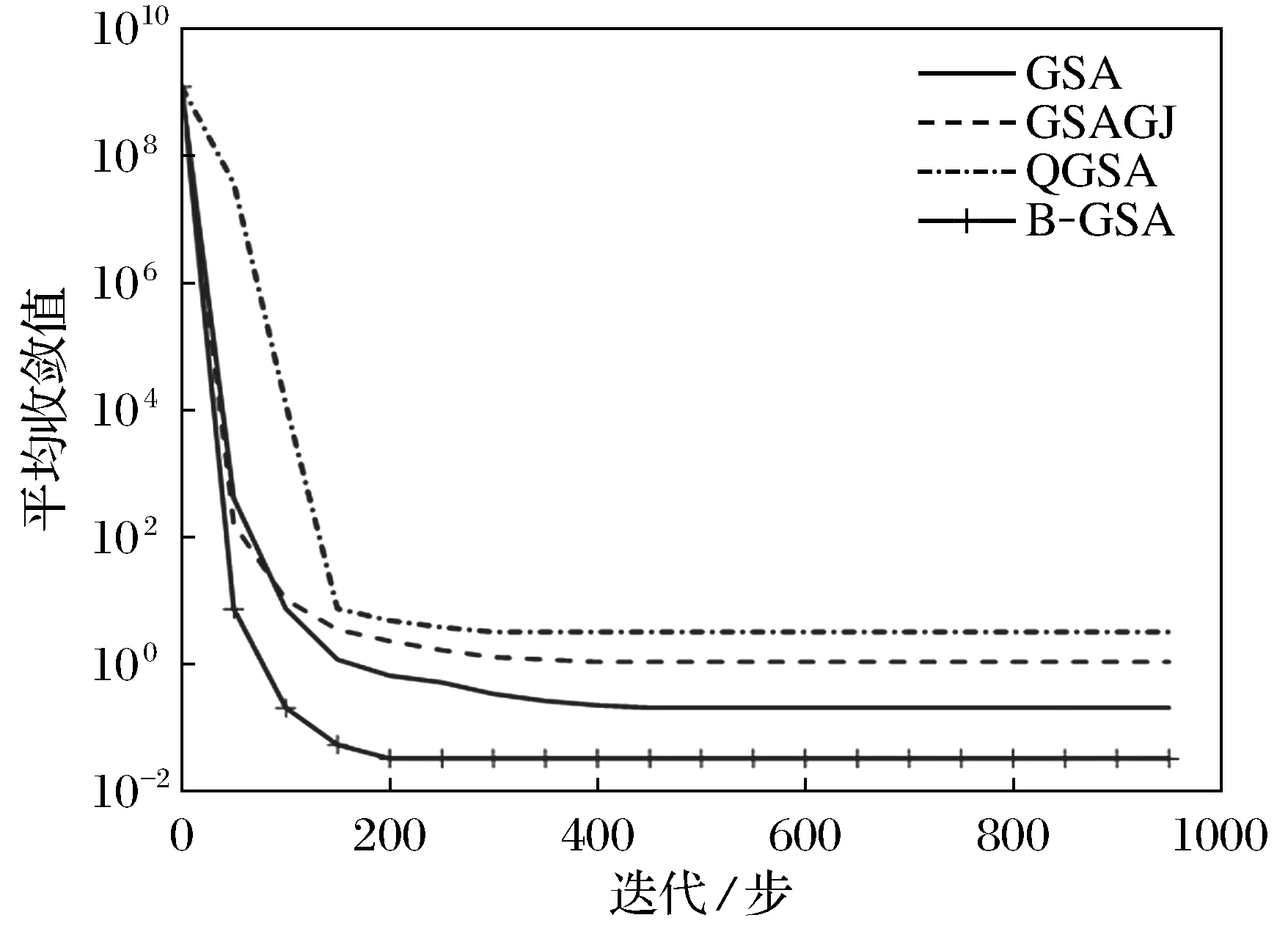
7) 在[0,1]中隨機選取一個隨機數r,若r

8) 計算每個粒子適應值,更新最好粒子;

9) 若算法滿足終止條件,則輸出最好適應值,否則轉步2.

3 數值實驗

為檢驗本文算法性能,選用文獻[20]中10個基準測試函數進行實驗。實驗在MATLAB7.0,Windows 7操作系統,2.00GB RAM 內存和2.10 GHz CPU環境下運行所有程序,且每個實驗獨立運行30次。表2給出了實驗所用到的基準測試函數,其中:D表示函數的維數;Ω是搜索區間;fopt表示最優值。

表2 衰減率為高斯函數、鐘型函數、Sigmoid函數的GSA的比較結果

表2顯示的是基于不同衰減率本文算法的數值結果,其中:G-GSA,B-GSA和S-GSA分別表示質量衰減率為高斯函數、鐘型函數、Sigmoid函數定義的質量衰減的GSA;best、worst、mean和std分別表示30次實驗中最好適應值、最差適應值、平均適應值和標準差。

表3 B-GSA與GSA,GSAGJ和QGSA比較結果

從表2可以看出,對于最好適應來說,在函數F7和F9上G-GSA優于其他2種算法,在函數F3,F4,F5,F6和F10上B-GSA優于其他2種算法,在F1,F2和F8上S-GSA優于其他2種算法;對于最差適應值來說,在函數F9上G-GSA優于其他2種算法,在函數F3,F4,F5,F6,F7和F10上B-GSA優于其他2種算法,在F1,F2和F8上S-GSA優于其他2種算法;對于平均適應值來說,在函數F6和F9上G-GSA優于其他2種算法,在函數F3,F4,F5,F7和F10上B-GSA優于其他2種算法,在F1,F2和F8上S-GSA優于其他2種算法.綜合考慮可以看出,B-GSA優于其他2種算法。

用B-GSA與GSA,GSAGJ[17]和QGSA[18]3種算法進行比較.比較結果見表3。從表3可以看出,B-GSA與GSA相比,對于最好適應值的指標,在函數F3,F4,F6,F7和F9上B-GSA優于GSA,在函數F1,F2和F8上B-GSA略好于GSA,但在F5和F10上GSA優于B-GSA;對于最差適應值指標,在函數F1,F3,F4,F5,F6,F7,F9和F10上B-GSA優于GSA,在函數F2和F8上B-GSA略好于GSA;對于平均適應值指標,在函數F1,F3,F4,F5,F6,F7,F9和F10上B-GSA優于GSA,在函數F2和F8上B-GSA略好于GSA。B-GSA與GSAGJ相比,對于最好適應值的指標,在函數F3,F4,F6,F7和F9上B-GSA優于GSAGJ,在函數F2和F8上B-GSA略好于GSA,但在F5和F10上GSAGJ優于B-GSA,在函數F1上GSAGJ略優于B-GSA;對于最差適應值指標,在函數F1,F3,F4,F5,F6,F7,F9和F10上B-GSA優于GSAGJ,在函數F2上B-GSA略好于GSAGJ;對于平均適應值指標,在函數F3,F4,F5,F6,F7,F9和F10上B-GSA優于GSAGJ,在函數F1,F2和F8上B-GSA略好于GSAGJ.B-GSA與QGSA相比,對于最好適應值來說,在函數F1,F3,F4,F5,F6,F9和F10上,B-GSA優于QGSA,在函數F8上,B-GSA略優于QGSA,但在函數F2和F7上,QGSA優于B-GSA,對于適應值最差來說,在函數F1,F3,F4,F5,F9和F10上,B-GSA優于QGSA,在函數F2和F8上,B-GSA略優于QGSA,但在函數F7上,QGSA優于B-GSA,在函數F6上,QGSA略優于B-GSA;對于平均適應值來說,在函數F1,F3,F4,F5,F9和F10上,B-GSA優于QGSA,在函數F8上,B-GSA略優于QGSA,但在函數F6和F7上,QGSA優于B-GSA,在函數F2上,QGSA略優于B-GSA。對于標準差來說,除了函數F5和F10外,B-GSA都有較好穩定性.綜上所述,B-GSA提高了算法的尋優能力和求解精度。

為比較各算法性能,圖1～圖6分別表示4種算法在函數F1,F3,F5,F7,F9,F10上的適應值收斂曲線。

圖1 函數F1的尋優曲線

圖2 函數F3的尋優曲線

圖3 函數F5的尋優曲線

圖4 函數F7的尋優曲線

從圖1～圖6中可以看出,B-GSA在函數F3,F9,F10的收斂速度上明顯優于其他3種算法,在函數F1和F5上,B-GSA的收斂速度相差不多,在函數F7上,QGSA明顯優于其他3種算法,總之,B-GSA能夠提高了算法的收斂速度。

圖5 函數F9的尋優曲線

圖6 函數F10的尋優曲線

4 小 結

在引力搜索算法(GSA)中,引力搜索算法易陷入局部最優,為提高算法的探索與開發能力,用隸屬度函數定義粒子質量的衰減率并給出一個新的變異算子,從而提出了慣性質量衰減的引力搜索算法。數值實驗結果顯示所提出的算法在求解精度與收斂速度明顯優于標準引力搜索算法、基于權值的引力搜索算法及基于高斯變異的引力搜索算法。在未來的工作中,進一步研究更好的衰減率。

[ 1 ]TANG K, MAN K, KWONG S, et al. Genetic algorithms and their applications[J]. IEEE Signal Process Mag, 1996,13(6):22-37.

[ 2 ]DORIGO M, MANIEZZO V, COLORNI A. The ant system: optimization by acolony of cooperating agents[J]. IEEE Trans Syst Man Cybern B, 1996,26(1):29-41.

[ 3 ]BERGH F, ENGELBRECHT A. A study of particle swarm optimization particle trajectories[J]. Inf Sci, 2006,176(8):937-971.

[ 4 ]KENNEDY J, EBERHART R. Particle swarm optimization[C]∥Proceedings of IEEE International Conference on Neural Networks, Perth WA: IEEE Press, 1995:1942-1948.

[ 5 ]KIRKPATRICK S, GELATTO C, VECCHI M P. Optimization by simulated annealing[J]. Science, 1953,220:671-680.

[ 6 ]KARABOGA D, BASTURK B. On the performance of artificial bee colony(ABC) algorithm[J]. Appl Soft Comput, 2008,8(1):687-697.

[ 7 ]RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. GSA: a gravitational search algorithm[J]. Inf Sci, 2009,179(13):2232-2248.

[ 8 ]RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. BGSA: binary gravitational search algorithm[J]. Nat Comput, 2010,9(3):727-745.

[ 9 ]谷文祥,李向濤,朱磊,等. 求解流水線調度問題的萬有引力搜索算法[J]. 智能系統學報, 2010,5(5):411-418.

[10]RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. Filter modeling using gravitational search algorithm[J]. Eng Appl Artif Intell, 2011,24(1):117-122.

[11]YIN M,HU Y, YANG F, et al. A novel hybrid K-harmonic means and gravitational search algorithm approach for clustering[J]. Expert Syst Appli, 2011,38(8):9319-9324.

[12]劉伯穎,張素琪,張麗麗. 一種引力搜索和K-means的混合聚類算法[J]. 河北工業大學學報, 2013,42(3):23-27.

[13]SUN G, ZHANG A. A hybrid genetic algorithm and gravitational search algorithm for image segmentation using Multilevel Thresholding[J]. Pat Recognit Image Anal, 2013,7887:707-714.

[14]曹茂俊,李盼池,尚福華. 量子行為引力搜索算法[J]. 控制與決策, 2016,31(9):1678-1684.

[15]TSAI H C, TYA N Y Y, WU Y W, et al. Gravitational Particle Swarm[J]. Appl Math Comput, 2013,219(17):9106-9117.

[16]張明,田娜,紀志成,等. 基于小生境技術的改進引力搜索算法[J]. 南京航空航天大學學報, 2016,48(5):753-760.

[17]徐遙,王士同. 引力搜索算法的改進[J]. 計算機工程與應用, 2011,47(35):188-192.

[18]隋永霞,孫合明. 基于高斯變異的引力搜索算法[J]. 江南大學學報(自然科學版), 2015,14(5):596-600.

[19]王奇琪,孫根云,王振杰等. 基于斥力的引力搜索算法[J]. 計算機科學, 2015,42(9):240-245.

[20]YAO X, LIU Y, LIN G. Evolutionary programming made faster[J]. IEEE Trans Evol Comput, 1999,3(2):81-102.

Gravitational search algorithm with inertial mass attenuation

QIAN Weiyi, ZHANG Lijia

(College of Mathematics and Physics, Bohai University, Jinzhou 121000, China)

In order to overcome the shortcomings that gravitational search algorithm (GSA) traps into local optima easily, a gravitational search algorithm with inertial mass attenuation is proposed. In this algorithm, the particle’s inertial mass is considered to have certain attenuation, the attenuation rate of particle's inertial mass is regarded as a fuzzy variable, the attenuation rate is defined based on membership functions, the particle’s inertial mass is redefined by the product of attenuation rate and particle’s inertial mass. Such exploitation ability of the proposed algorithm is improved. In addition, a new mutation operator is proposed to improve the exploration ability. Finally, the proposed algorithm is tested on several benchmark test functions and compared with GSA and the other improved GSA. The numerical results indicate that the proposed algorithm can improve the convergence speed and precision.

gravitational search algorithm; membership function; mutation operator; global optimization

1673-5862(2017)02-0138-07

2017-02-06。

國家自然科學基金資助項目(11371071); 遼寧省教育廳科學研究一般項目(L2013426)。

錢偉懿(1963-),男,遼寧錦州人,渤海大學教授,博士。

TP18

A

10.3969/ j.issn.1673-5862.2017.02.003