供給側視角下的智能電網商業模式研究

李付林+周建其+曾建梁+厲俊++方景輝

摘要：智能電網在商業模式上的研究有時比在技術應用上的研究更重要。研究了供給側視角下能源供應商的博弈行為和收益。從穩定性分析和數值仿真的角度分析了能源供應商的穩態收益，并研究了穩態條件下能源供應商的利潤增長方式。結果表明合理的產量和價格策略可以最大化能源供應商的利潤。

Abstract： Research on business model is more important than that on technology and application sometimes. Game behavior and revenue of energy suppliers in a supply-side view are studied. Steady revenues of energy suppliers are analyzed in the method of stability analysis and numerical simulation， and profit growth of energy suppliers in steady state is researched. Result shows that reasonable yield and price strategy can maximize energy suppliers' profits.

關鍵詞：智能電網；商業模式；供給側視角；穩定性分析；數值仿真

Key words： smart grid；business model；supply-side view；stability analysis；numeric simulation

中圖分類號：F426 文獻標識碼：A 文章編號：1006-4311（2017）17-0206-03

0 引言

新能源技術和互聯網技術作為工業4.0的核心技術正在推動分布式可再生能源的大規模利用與分享，促進電力、交通、天然氣等多種復雜網絡系統的相互融合[1]。智能電網是能源互聯網的重要組成部分，和現在的電網體系是完全不同的“生態系統”，且發展智能電網需要發展技術、標準和商業模式。其中，商業模式對智能電網的發展尤為關鍵[2]。因此研究基于互聯網思維的智能電網新型商業模式是非常有意義的。

能源市場是一個典型的寡頭市場，目前已有很多學者對其展開了研究[3-5]，這些研究主要以博弈論作為工具[6]。智能電網的一個重要特征就是能源產品和增值產品共存[7]。本文從供給側[8]視角入手，建立了能源供應商的Cournot雙寡頭模型，從穩定性分析和數值仿真的角度分析了能源供應商的博弈行為和穩態收益，并研究了穩態條件下能源供應商的利潤增長方式。

1 模型建立

考慮一個雙寡頭的能源市場，其中有兩個能源供應商，記為能源供應商1，2。能源供應商1生產A，B兩種產品，能源供應商2生產A，C兩種產品。其中A是能源產品，B，C是增值產品，B，C均是A的互補產品。由于產品A，B和A，C之間的互補性，不妨設A的用戶以一定的比例η1，η2使用增值產品B，C。即QB=η1QA1，QC=η2QA2，其中QA1，QA2是廠商1，2生產A的產量，QB，QC是產品B，C的產量。能源供應商1，2供應的A是同質的，A的市場是一個寡頭競爭市場；能源供應商1，2供應的B，C是異質的，B，C的市場各自是一個壟斷市場。產品A，B，C的價格函數為：

（1）

能源供應商1，2的利潤函數為：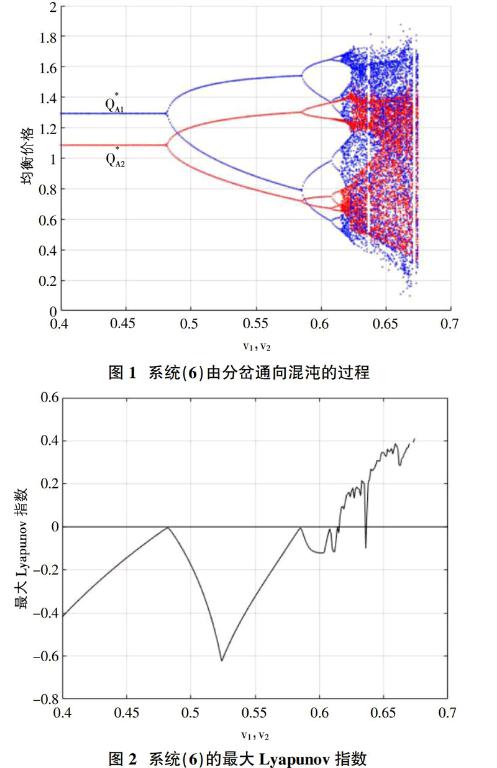

（2）

其中PA，PB，PC表示產品A，B，C的價格，kA1，kB表示供應商1生產產品的成本，kA2，kC表示供應商2生產產品A，C的成本，a，b，c，d，e，f是正參數。

基于能源供應商利潤最大化的動機，t+1時刻能源供應商i生產產品的產量是如下最優化問題的解：

（3）

對產量的邊際利潤：

（4）

能源供應商1，2彼此不知道對方下一時刻的產量，采取“有界理性策略”[9]，即：

（5）

聯合（4）（5），得到：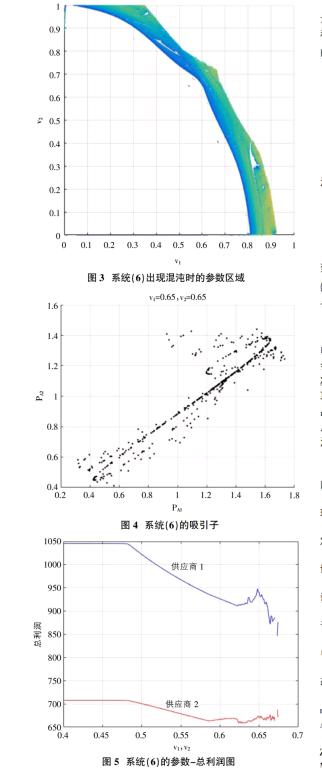

（6）

2 模型分析

2.1 穩定性分析

系統（6）關于QA1，QA2的平衡點是如下方程的解：

（7）

得到：

（8）

其中：

（9）

E1，E2，E3含有零點，因此它們是邊界均衡點，意味著有能源供應商會退出博弈。E4是有納什均衡點。設E4的特征方程為：

（10）

根據Jury原則，E4是穩定的當且僅當：

（11）

2.2 數值仿真

我們引入總利潤指標[10]來表示能源供應商的總利潤：

（12）

其中Li（QA1（t），QA2（t））表示能源供應商i在t時刻博弈的利潤，L表示能源供應商i在t=1，2，…，T時刻的總利潤。

利用Matlab進行數值仿真，得到圖1-5。圖1顯示的是系統（6）由倍周期分岔通向混沌的過程。圖2顯示的是最大Lyapunov指數。圖3顯示的是系統（6）出現混沌時參數（v1，v2）的區域。圖4顯示的是取不同值時系統（6）的吸引子。圖5顯示的是v1，v2兩個能源供應商對參數v1，v2的總利潤圖。

由以上的數值結果可以得到如下結論：對于傳統商業模式下的Cournot雙寡頭模型而言，隨著“有界理性”能源供應商調節自身產品價格速度的變化，該博弈模型會出現分岔，混沌等復雜的動力學行為，兩個能源供應商的總利潤也會隨著減少。這意味著在現實世界中，能源供應商之間會不斷調整產量而使市場能源供應混亂，能源供應商們的總利潤也會減少。

2.3 穩態分析

當市場到達穩態時，供應商1，2均不會改變A的產量。這意味著能源產品A為供應商1，2提供的利潤已經穩定，需要從增值產品B，C入手提升供應商的利潤。設此時供應商1，2生產的A分別為Q，Q，公式（1）變為：

（13）

此時的PA為常值。聯合公式（2）得到：

（14）

供應商1，2的利潤轉化為關于PB，PC函數，其邊際利潤為：

（15）

當PB=（c+kB）/2，PC=（e+kC）/2時，供應商1，2的利潤達到最大。此時的增值產品占能源產品的比例分別為η1=（c-kB）/2dQ，η2=（e-kC）/2fQ。研究表明對增值產品采取合適的定價策略可以使穩態下的廠商利潤最大化。

3 結束語

本文研究了供給側視角下能源供應商的博弈行為和收益。結果表明，能源供應商以較快的速度調節自身產量會引發市場能源供應的不穩定，也會造成供應商獲得利潤減少。當市場達到穩態時，能源供應商可以對增值產品采取適當的定價策略增加利潤。本文的結果證明了“能源產品+增值產品”這種商業模式的有效性，并給出了“對能源產品定量，對增值產品定價”的策略使得能源供應商的利潤最大化。

參考文獻：

[1]董朝陽，趙俊華，文福拴，薛禹勝.從智能電網到能源互聯網：基本概念與研究框架[J].電力系統自動化，2014（15）：1-11.

[2]黃家嘉.商業模式對智能電網發展的影響[J].企業改革與管理，2014（15）：63-64.

[3]韋加雄，昌健，王莉芳，李強，董穩改.不確定策略對發電側定價的激勵機制研究[J].電力科學與工程，2015（07）：30-33.

[4]于維生，于羽.基于伯川德推測變差的有限理性動態寡頭博弈的復雜性[J].數量經濟技術經濟研究，2013（02）：126-137.

[5]張榮，張宗益.電力競價博弈中的信息結構[J].系統工程理論與實踐，2013（01）：92-98.

[6]盧強，陳來軍，梅生偉.博弈論在電力系統中典型應用及若干展望[J].中國電機工程學報，2014（29）：5009-5017.

[7]吳晨，李揚，王蓓蓓.智能電網用電增值服務的發展方向[J].電力需求側管理，2012（05）：44-47.

[8]曾鳴，張曉春，王麗華.以能源互聯網思維推動能源供給側改革[J].電力建設，2016（04）：10-15.

[9]E.M. Elabbasy， H.N. Agiza， A.A. Elsadany. Analysis of nonlinear triopoly game with heterogeneous players， Comput Math Appl 57（2009）： 488-499.

[10]Jianguo Du， Tingwen Huang， Zhaohan Sheng， Haibin Zhang. A new method to control chaos in an economic system， Appl Math Comput 217 （2010）： 2370-2380.

[11]莫凡.“免費午餐”背后的秘密[J].中國財政，2014（06）：66-67.