測度微分方程的變差穩定性
李寶麟, 張珍珍
(西北師范大學 數學與統計學院, 甘肅 蘭州 730070)
測度微分方程的變差穩定性
李寶麟, 張珍珍
(西北師范大學 數學與統計學院, 甘肅 蘭州 730070)
利用廣義常微分方程的穩定性理論,定義了測度微分方程變差穩定性和變差漸近穩定性概念,建立了測度微分方程的變差穩定性和變差漸近穩定性定理.
測度微分方程; 變差穩定; 變差漸近穩定; 廣義常微分方程
Dx=f(t,x)+g(t,x)Du,
(1)
其中Dx、Du代表函數x和函數u的分布導數.如果u是有界變差函數,則Du為Lebesgue-Stieltjes測度,并且Du是u的不連續點對突然改變系統狀態的影響.形如(1)式的方程叫作測度微分方程[1].測度微分方程(1)的解x(·)是有界變差函數,它的分布導數滿足方程(1).W. W. Schmaedeke[1]對方程(1)的特殊情況進行了研究,其中g不依賴于x,即g(t,x)=g(t),并且為了在后面的分析中利用Riemann-Stieltjes積分的方法假設它是t的連續函數.
測度微分方程(包含更多抽象的測度微分方程見文獻[2])已經被很多作者研究[1,3-5].測度泛函微分方程[6-7]代表了一類特殊的測度微分方程.時標上的泛函動力方程代表了一類特殊的測度泛函微分方程.近年來,這2類方程已經被大量地研究了.文獻[8]已經給出了測度微分方程的一些性質.2013年,Meng G.等[9]從測度的連續依賴性角度研究了測度微分方程.M. Federson等[10]討論了時滯型泛函微分方程的穩定性.T. Faria等[11]討論了無限時滯的脈沖微分方程的穩定性.P. C. Das等[5]討論了測度微分方程解的存在性和穩定性,不過他們討論的是擬等度漸近穩定性和指數漸近穩定性.
測度微分方程是描述具有脈沖行為的微分系統,其解是不連續的有界變差函數.測度微分方程可以轉化為廣義常微分方程[12].文獻[12]介紹了廣義常微分方程的穩定性理論.本文利用廣義常微分方程的穩定性理論,首次提出測度微分方程變差穩定和變差漸近穩定的概念,定義了測度微分方程變差穩定性和變差漸近穩定性,并建立了測度微分方程變差穩定性定理和變差漸近穩定性定理來討論測度微分方程.
1 預備知識
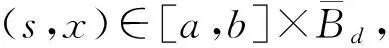
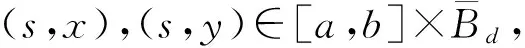
‖f(s,x)-f(s,y)‖≤l1(s)ω1(‖x-y‖)
成立,其中ω1:[0,+∞)→R是連續增函數,且ω1(0)=0.

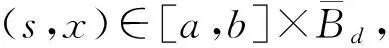
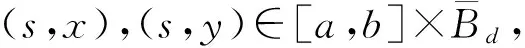
引理 1.1[8]一個函數x(·):[α,β]→Rn,[α,β]?[0,+∞)是測度微分方程(1)在區間[α,β]上通過(t0,x0)的一個解,當且僅當對t0,t∈[α,β]它滿足積分方程
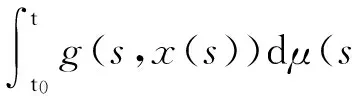
(2)
給定一個函數δ:[a,b]→(0,+∞).如果有[αi-1,αi]?[τi-δ(τi),τi+δ(τi)],i=1,2,…,k,區間[a,b]上的一個分劃D:a=α0<α1<…<αk=b和標記τi∈[αi-1,αi]稱為δ-精細分劃.
定義 1.1[12]函數U:[a,b]×[a,b]→Rn+1在區間[a,b]上稱為Kurzweil可積的,如果存在向量I∈Rn+1,對任意的ε>0,在區間[a,b]上存在正值函數δ,使得對區間[a,b]上的任何δ-精細分劃D,都有
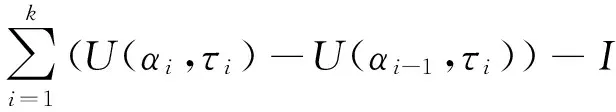
定義 1.2[12]G=[a,b]×Bd,G?Rn+1.假設F:G→Rn,函數x:[α,β]→Rn,如果(t,x)∈G在區間[α,β]?[a,b]對所有的t∈[α,β],s1,s2∈[α,β]有
則稱函數x為廣義常微分方程
(4)
的解.
定義 1.3[12]設函數F:G→Rn,如果F屬于函數族R(G,h,ω),則對所有的(s1,x),(s2,x)∈G有
‖F(s2,x)-F(s1,x)‖≤|h(s2)-h(s1)|, (5)
且對所有的(s1,x),(s2,x),(s1,y),(s2,y)∈G有
‖F(s2,x)-F(s1,x)-F(s2,y)+F(s1,y)‖≤
ω(‖x-y‖)|h(s2)-h(s1)|,
(6)
其中h:[0,+∞)→R為不減函數,ω:[0,+∞)→R為連續的增函數且ω(0)=0.

(7)
存在不減函數h2:[a,b]→R,使得不等式
‖F2(t2,x)-F2(t1,x)‖≤|h2(t2)-h2(t1)|
和
‖F2(t2,x)-F(t1,x)-F(t2,y)+F(t1,y)‖≤
ω2(‖x-y‖)|h2(t2)-h2(t1)|

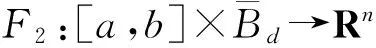
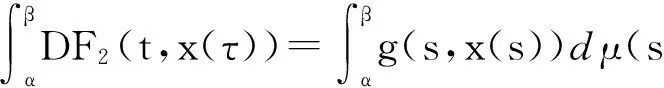
引理 1.4[12]一個函數x:[α,β]→Rn,[α,β]?[a,b]是測度微分方程(1)在區間[α,β]上的解,當且僅當x是廣義常微分方程
(8)
在區間[α,β]上的解,且
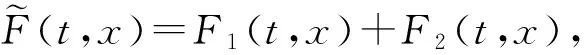
定義 1.4 如果對于任意的ε>0,存在δ=δ(ε)>0,使得若y:[t0,t1]→Rn,0≤t0 (9) 對任意的t∈[t0,t1]有 ‖y(t)‖<ε, 則稱測度微分方程(1)的解x≡0是變差穩定的. 定義 1.5 如果存在δ0>0,并且對任意的ε>0有T=T(ε)≥0和γ=γ(ε)>0,使得若y:[t0,t1]→Rn,0≤t0 (10) 對任意的t∈[t0,t1]∩[t0+T(ε),+∞),且t0≥0時有 ‖y(t)‖<ε, 則稱測度微分方程(1)的解x≡0是變差吸引的. 定義 1.6 如果測度微分方程(1)的解x≡0既是變差穩定的又是變差吸引的,則稱測度微分方程(1)的解x≡0是變差漸近穩定的. 引理 1.5[12]假設-∞ φ(σ+η)-φ(σ)≤ψ(σ+η)-ψ(σ) (11) 成立,則對所有的t∈[a,b]有 φ(t)-φ(a)≤ψ(t)-ψ(a). (12) 引理 1.6 假設V:[0,+∞)×Rn→R是使得對任意的x∈Rn,函數V(·,x):[0,+∞)→R在區間(0,+∞)上是左連續的,假設: (i) 對(t,x),(t,y)∈[0,+∞)×Rn和常數K>0有 (13) (ii) 存在一個實函數Φ:Rn→R,使得對于廣義常微分方程(8)在區間[α,β]?[0,+∞)上的所有解x:(α,β)→Rn對于t∈(α,β)有 (14) 如果y:[t0,t1]→Rn,0≤t0 (15) 本章討論測度微分方程(1)的變差穩定性和變差漸近穩定性. (i) 存在一個連續遞增實函數b:[0,+∞)→R使得b(ρ)=0當且僅當ρ=0; V(t,x)≥b(‖x‖); (16) V(t,0)=0 (17) 和 ‖V(t,x)-V(t,y)‖≤K‖x-y‖. (18) 如果函數V(t,x(t))對測度微分方程(1)的任何一個解x(t)是不增函數,則(1)式的平凡解x≡0是變差穩定的. 證明 令 其中x∈Bd,t0,t∈[a,b]. 由于m1(s)在區間[a,b]上是非負的,所以φ1(t)是區間[a,b]上的非減函數. 由于l1(s)在區間[a,b]上是非負的,所以ψ1(t)是區間[a,b]上的非減函數. 令h1(t)=φ1(t)+ψ1(t),可知函數F1屬于函數族R(G,h1,ω1).類似的,令 有 由于m2(s)在區間[a,b]上是非負的,所以φ2(t)是區間[a,b]上的非減函數. 由于l2(s)在區間[a,b]上是非負的,所以ψ2(t)是區間[a,b]上的非減函數.令h2(t)=φ2(t)+ψ2(t),由上可知,函數F2屬于函數族R(G,h2,ω2). 下面證明測度微分方程(1)的平凡解x≡0是變差穩定的.由于假設函數V(t,x(t))對測度微分方程(1)的任何一個解x:[α,β]→Rn是非增函數,即對廣義常微分方程(8)的任何一個解x:[α,β]→Rn也成立,所以對t∈[α,β]有 下面證明在這種假設下定義1.4中的條件是滿足的.給定ε>0,令y:[t0,t1]→Rn是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續.由于函數V滿足引理1.6中的(14)式,其中Φ≡0.由(15)、(17)和(18)式,對于任意的t∈[t0,t1]可得 (20) 則由(20)式有 V(r,y(r))≤K‖y(t0)‖+Kδ(ε)≤ 所以,當r∈[t0,t1]時可以得到 V(r,y(r))≤2Kδ(ε). (21) 如果存在一個ξ∈[t0,t1],使得‖y(ξ)‖≥ε,則由(16)式可得 這與(21)式矛盾.因此,對所有的t∈[t0,t1]有‖y(t)‖<ε.由定義1.4可知測度微分方程(1)的解x≡0是變差穩定的. (22) 成立,其中Φ:Rn→R是連續,Φ(0)=0;當x≠0時,Φ(x)>0.則測度微分方程(1)的平凡解x≡0是變差漸近穩定的. 證明 由(8)式,顯然函數V(t,x(t))對測度微分方程(1)的任何一個解x:[α,β]→Rn是非增函數.因此,由定理2.1可知測度微分方程(1)的平凡解x≡0是變差穩定的.根據定義1.6,還需證明解是變差吸引的. 根據定義1.4測度微分方程(1)的平凡解x≡0變差穩定性的概念可知:存在一個δ0∈(0,d),使得若y:[t0,t1]→Rn是[t0,t1]上的有界變差函數,其中0≤t0 則對t∈[t0,t1]有‖y(t)‖ 對任意的ε>0,由測度微分方程(1)的平凡解x≡0的變差穩定性知:存在一個δ(ε)>0,使得對任意的y:[t2,t3]→Rn是[t2,t3]上的有界變差函數,其中0≤t2 ‖y(t0)‖<δ(ε), (23) 且有 (24) 則對t∈[t2,t3]有 ‖y(t)‖<ε. (25) M=sup{-Φ(x);γ(ε)≤‖x‖<ε}= 并且假設y:[t0,t1]→Rn是[t0,t1]上的有界變差函數,其中0≤t0 (26) 假設T(ε) 因此 V(t0+T(ε),y(t0+T(ε)))≤ 這與不等式 V(t0+T(ε),y(t0+T(ε)))≥ 矛盾.因為(23)和(24)式成立,且當t1=t*或t1=t3時,(25)式也滿足.所以必定存在一個t*∈[t0,t0+T(ε)],使得‖y(t*)‖<γ(ε).因此,對t>t0+T(ε)時有‖y(t)‖<ε.由于t*∈[t0,t0+T(ε)],因此測度微分方程(1)的解x≡0是變差漸近吸引的.所以由定義1.6可知:測度微分方程(1)的平凡解x≡0是變差漸近穩定的. [1] SCHMAEDEKE W W. Optimal contral theory for nonlinear vector differential equations containing measures[J]. SIAM Control,1965,3(2):231-280. [3] RAO M R M, RAO V S H. Stability of impulsively perturbed systems[J]. Bull Austral Math Soc,1977,16(1):99-110. [4] PANDIT S G. Differential systems with impulsive perturbations[J]. J Pacific Math,1980,86(2):553-560. [5] DAS P C, SHAMA R R. Existence and stability of measure differential equations[J]. Czech Math J,1972,22(97):145-158. [6] FEDERSON M, MESQITA J G, SLAVK A. Measure functional differential equations and functional dynamic equations on time scales[J]. J Diff Eqns,2012,252(6):3816-3847. [8] 徐遠通. 泛函微分方程與測度微分方程[M]. 廣州:中山大學出版社,1988:179-306. [9] MENG G, ZHANG M. Dependence of solutions and eigenvalues of measure differential equations on measures[J]. J Diff Eqns,2013,254(5):2196-2232. [10] FEDERSON M, SCHWABIK S. Stability for retarded functional differential equations[J]. Ukrainian Math J,2008,60(1):121-140. [11] FARIA T, GADOTTI M C, OLIVEIRA J J. Stability results for impulsive functional differential equations with infinite delay[J]. Nonlinear Anal:TMA,2012,75(18):6570-6587. [12] SCHMAEDEKE W W. Generalized Ordinary Differential Equations[M]. Singapore:World Scientific,1992. [13] KELLEY W G, PETERSON A C. The Theory of Differential Equations[M]. 2nd ed. New York:Springer-Verlag,2010. [14] SCHWABIK S, TVRDY M, VEJVODA O. Differential and Integral Equations:Boundary Value Problems Adjoints[M]. Berlin:Springer-Verlag,1979. 2010 MSC:30D35; 39A10; 39A12 (編輯 周 俊) Variational Stability for Measure Differential Equations LI Baolin, ZHANG Zhenzhen (CollegeofMathematicsandStatistics,NorthwestNormalUniversity,Lanzhou730070,Gansu) In this paper, we define notions of variational stability and variational-asymptotically stability for measure differential equations and establish their theories by using the theory of stability for generalized ordinary differential equations. measure differential equations; variational stability; variational-asymptotic stability; generalized ODE 2016-10-17 國家自然科學基金(11061031) 李寶麟(1963—),男,教授,主要從事微分方程應用的研究,E-mail:787535241@qq.com O175.12 A 1001-8395(2017)03-0328-06 10.3969/j.issn.1001-8395.2017.03.010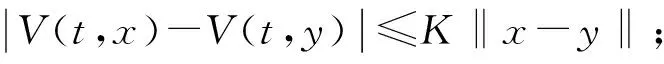
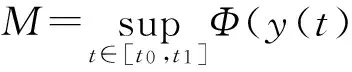
2 主要結論
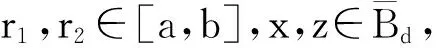
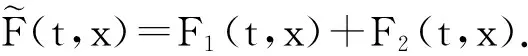
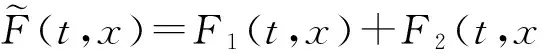
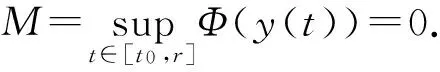
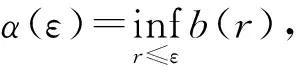
Kδ(ε)+Kδ(ε).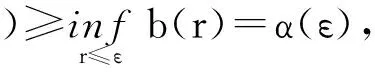
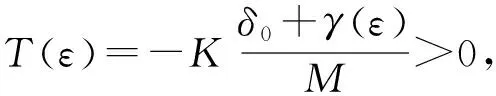
-inf{Φ(x);γ(ε)≤‖x‖<ε}<0,
V(t0,y(t0))-Kδ0≤
K‖y(t0)‖-Kδ0
b(‖y(t0+T(ε))‖)≥b(γ(ε))>0

