基于Laguerre函數對圓柱面繞射勢的數值逼近

李 輝，呂明冬，任慧龍，陳小波，田 博

（1.哈爾濱工程大學 船舶工程學院，哈爾濱 150001；2.中國船舶及海洋工程研究院，上海 200011；3.法國船級社深水技術研究中心，新加坡）

基于Laguerre函數對圓柱面繞射勢的數值逼近

李 輝1，呂明冬2，任慧龍1，陳小波3，田 博1

（1.哈爾濱工程大學 船舶工程學院，哈爾濱 150001；2.中國船舶及海洋工程研究院，上海 200011；3.法國船級社深水技術研究中心，新加坡）

無限深圓柱表面繞射勢沿水深方向的變化是連續的、不斷衰減的。基于無窮區間Laguerre多項式并引入的伸縮系數s定義了Laguerre函數，既保證了函數在無窮區間的正交性，又使函數具有靈活性。繞射勢的變化，可以用一系列Laguerre函數表示成級數形式。文中對該方法的收斂性進行了證明，并以一條FPSO為例對其在圓柱面的繞射勢進行了逼近。求解級數展開式的系數時會遇到無窮積分問題，采用多次使用Gauss-Legendre積分和Gauss-Laguerre積分相結合的方法代替傳統的Gauss-Laguerre積分方法，獲得更高的積分精度。利用Laguerre函數可以對Rankine源法或者Rankine-Kelvin法的控制面上速度勢進行逼近。

Laguerre函數；繞射勢；Gauss-Laguerre積分；Gauss-Legendre積分

0 引 言

在三維勢流理論中，速度勢用于計算船舶運動和載荷[1-2]，速度勢求解通常使用格林函數法，常用的格林函數方法有Rankine源法[3]、Kelvin源法[1]等。每種格林函數有自身優點，但同時又存在一些不足。例如：Rankine源法優點在于避免了復雜格林函數計算，沒有不規則頻率問題，但必須在整個無限自由面積分，需要在全部自由面劃分大量網格，除此之外，還需要建立一個阻尼區消除反射波的影響[1]。Kelvin源法優點是在自由面積分為零，無需對自由面劃分網格，對于簡單的物體，例如半球，圓柱有較好的結果，然而對于實際的船體它的波浪成分會引起計算結果震蕩以及收斂速度慢的問題[5]。

BV的陳小波博士[6]提出Rankine-Kelvin方法，即利用一個圓柱面作為控制面，將流體域分為兩部分，內域和外域。外域采用無航速格林函數，內域采用簡單格林函數。在外域，簡單的圓柱表面的速度勢和速度勢法向導數可以假設是已知的；在內域，船體表面的速度勢法向導數已知，控制面上的速度勢可以和外域方程聯合求解，因此只需要對物體表面以及控制面內有限自由表面劃分網格，就可以滿足求解條件。

速度勢中，繞射勢以及輻射勢是未知的，繞射勢與輻射勢的在圓柱控制面沿豎直方向上變化是相似的，利用Rankine-Kelvin方法求解時，圓柱控制面的任意點的繞射勢以及輻射勢是利用Laguerre函數表示，既可以不必在圓柱面上劃分網格，又在積分和微分上會獲得很大便利。本文為了探究該方法的可行性，以繞射勢為例，首先利用格林函數法可以求出實際物體在圓柱面上任意點的繞射勢，再利用Laguerre函數對繞射勢函數進行逼近，獲得繞射勢的級數展開形式，求出逼近誤差，檢驗是否滿足工程應用的精度。

本文結構如下。第1章定義Laguerre函數，并引進伸縮系數s，證明含有伸縮系數s的Laguerre函數具有正交性。第2章給出Laguerre函數逼近的具體步驟，對該方法收斂性進行證明。引入Gauss-Laguerre與Gauss-Legendre混合積分的方法，可以更準確地求出無窮積分的積分值。第3章給出計算的數值結果。

1 Laguerre函數

當ω=1時，定義為

n階Laguerre多項式定義如下[7]

該多項式滿足如下遞推關系[7]

Laguerre多項式是一個完全正交系，滿足如下正交關系[7]

其中：δl，m是Kronecker符號。

現定義Laguerre函數如下：

Laguerre函數也是一個完全正交系，滿足如下正交關系

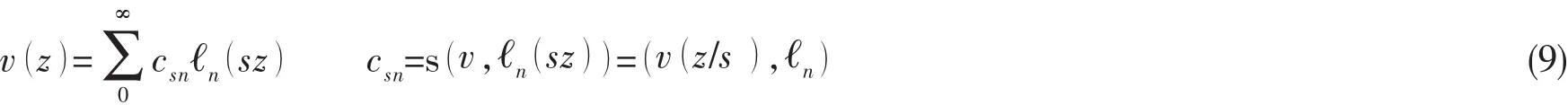
其中：?n（sz）也是完全正交系，滿足如下公式

證明如下：

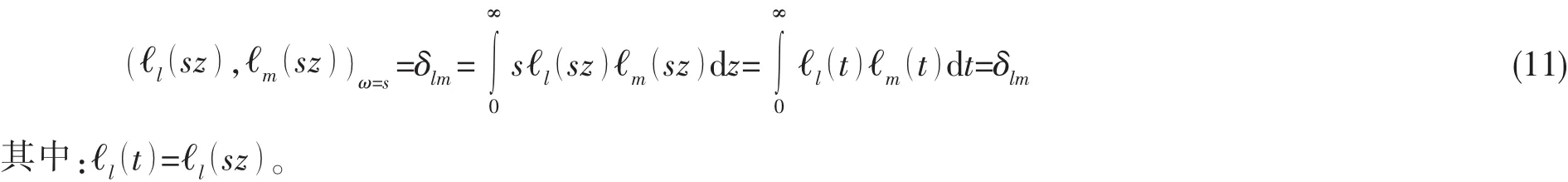
2 含伸縮系數Laguerre函數對速度勢函數展開

在離物體一定距離時，速度勢函數φ（z）沿深度的變化是連續的，當水深趨于無窮時，速度勢趨于零，所以速度勢函數表達式可以用下式表達：

由上述證明可知，當函數φ（z）滿足平方可積且連續的條件，則該函數基于Laguerre級數展開是絕對收斂的。由于函數f（z）=1/1+z平方可積，速度勢函數φ（z）收斂速度快于函數f（z）=1/1+z，則該速度勢函數φ（z）可以被級數展開。

采用高斯積分計算級數前系數csn，在［0，∞］做高斯積分，通常采用Gauss-Laguerre插值積分：

其中：zk′為Laguerre多項式的互異零點，理論上說，Gauss-Laguerre法的積分誤差隨著N增加而減少。不過，隨著N和k增加，特別是零點離積分原點非常遠的情況下，Laguerre多項式相鄰零點zk′與z′k+1距離會快速變大，對于特別大的N，相鄰零點之間距離可以達到4N[8]，這個特征既是Gauss-Laguerre積分法的優點也是缺點。它意味著可以用適當的N可以計算無窮區域的積分，但事實上如果被積函數在相鄰零點間震蕩比較劇烈，可能就無法準確得到兩個零點間的積分值。為了改進這一缺點，本文采用Gauss-Laguerre與Gauss-Legendre相結合的方法，Gauss-Legendre方法優點在于可以將震蕩衰減函數的震蕩部分分成n個有限積分區間，每個有限積分區間采用Gauss-Legendre積分法積分，可以保證震蕩區間有足夠的計算數值點，對于收斂部分，可以采用Gauss-Laguerre積分法積分。具體步驟如下：

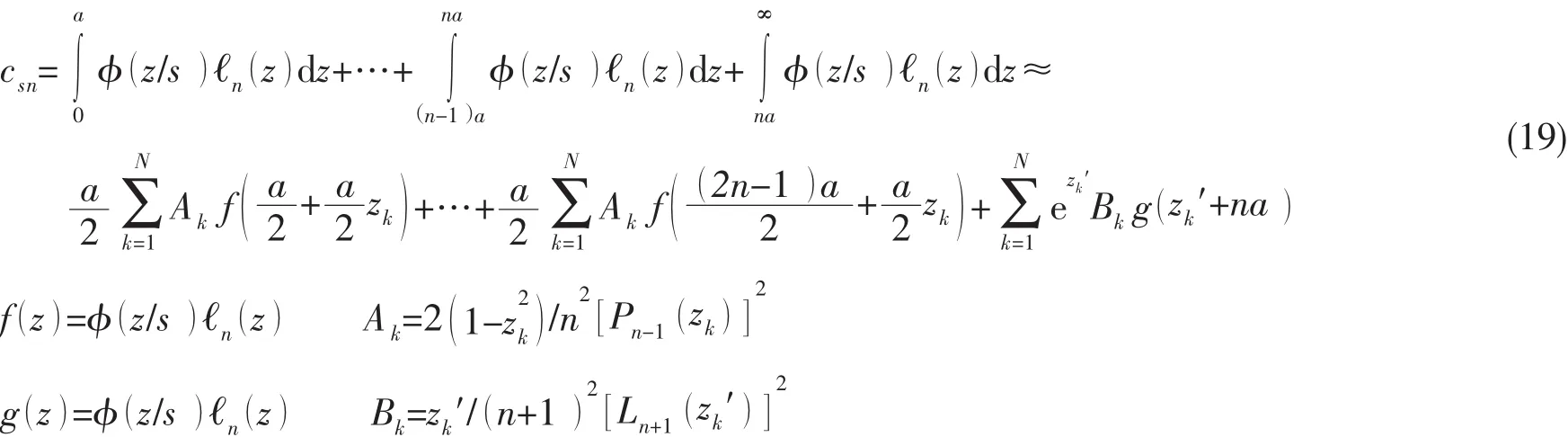
其中：zk為N階Legendre多項式零點，zk′為N階Laguerre多項式零點。

現在，選取函數在F（z）=（e-cz，J0（dz）），被積函數f（z）=e-czJ0（dz）為震蕩衰減函數，積分可得解析解，相對誤差Er定義為

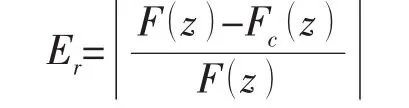
其中：F（z）為真實值，Fc（z）為數值計算值，利用混合積分法數值計算得到的積分值，見表1。

表1 混合積分法得到數值解與相對誤差Tab.1 Numerical results and relative error with composite integration

表1中，n=1時為Gauss-Laguerre積分方法。由表1可見，隨著Gauss-Legendre積分區間個數n增加，積分精度有較快提高，在實際應用中，可以預先設置一個誤差值，n個區域的積分值和n+1個區域積分值差值絕對值小于設定誤差值，可以認為得到高精度數值解。

3 算 例

本文以一條長225 m，寬36 m，平均吃水16 m的FPSO為計算模型，選取船中為中心半徑為450 m無限深圓柱為控制面，計算航速為0 kn，計算頻率分別為ω=0.17 rad/s，0.6 rad/s，1.7rad/s浪向為迎浪。本文采用 CCS認證的COMPASSWALCS-BASIC水動力載荷軟件為計算軟件，得到船艏方向控制面上的繞射勢，具體位置見圖1。

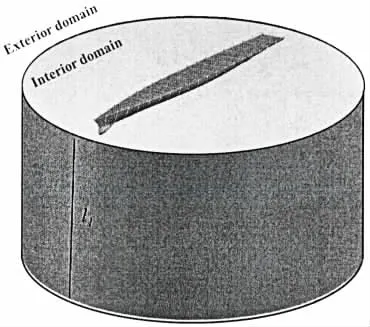
圖1 繞射勢在控制面上的逼近路徑Fig.1 Approximation path of diffraction potential on the control surface

由COMPASS-WALCS-BASIC計算出的繞射勢定義為φ7W，Laguerre函數逼近得到的繞射勢定義為φ7L。絕對誤差定義為E*，如下式

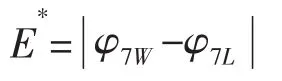
不同頻率下，l1繞射勢實部與虛部逼近值以及絕對誤差見圖2-7。n為級數展開項數，s為伸縮系數。

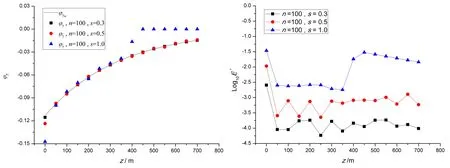
圖2 l1處繞射勢逼近值（實部）與絕對誤差（ω=0.17 rad/s）Fig.2 Diffracted approximation(real part)and absolute error along l1(ω=0.17 rad/s)

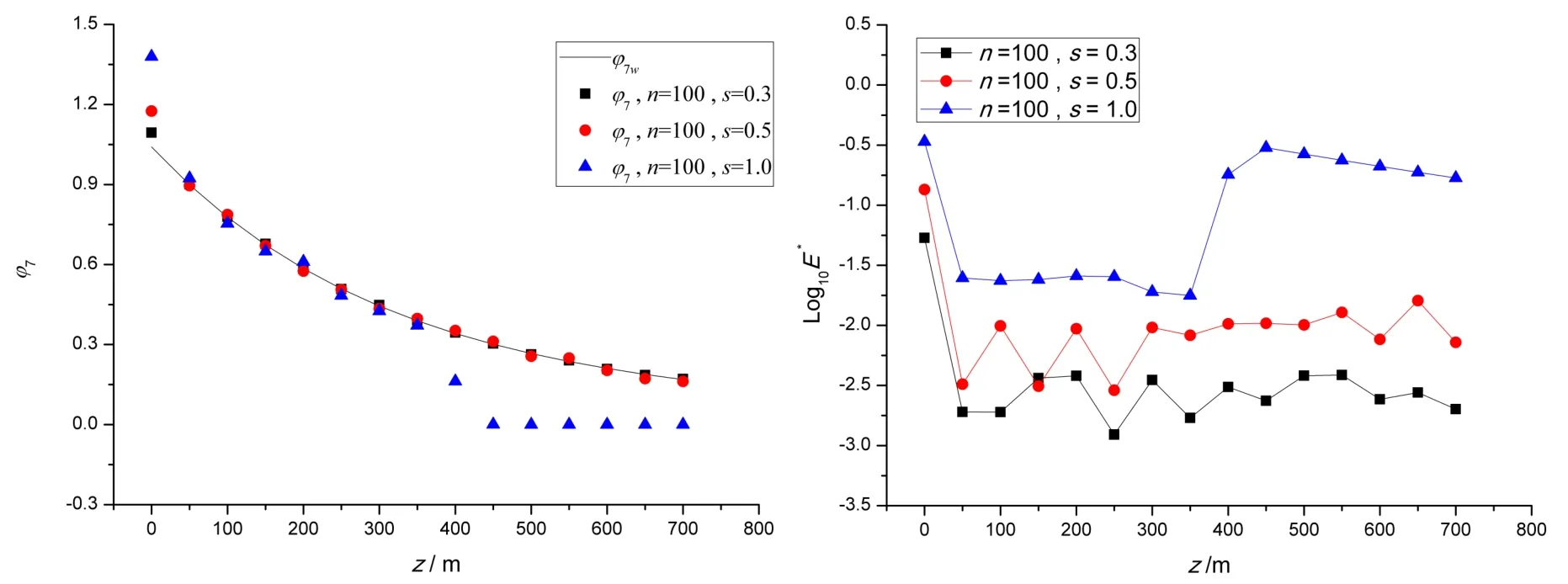
圖3 l1處繞射勢逼近值（虛部）與絕對誤差（ω=0.17 rad/s）Fig.3 Diffracted approximation(imaginary part)and absolute error along l1(ω=0.17 rad/s)

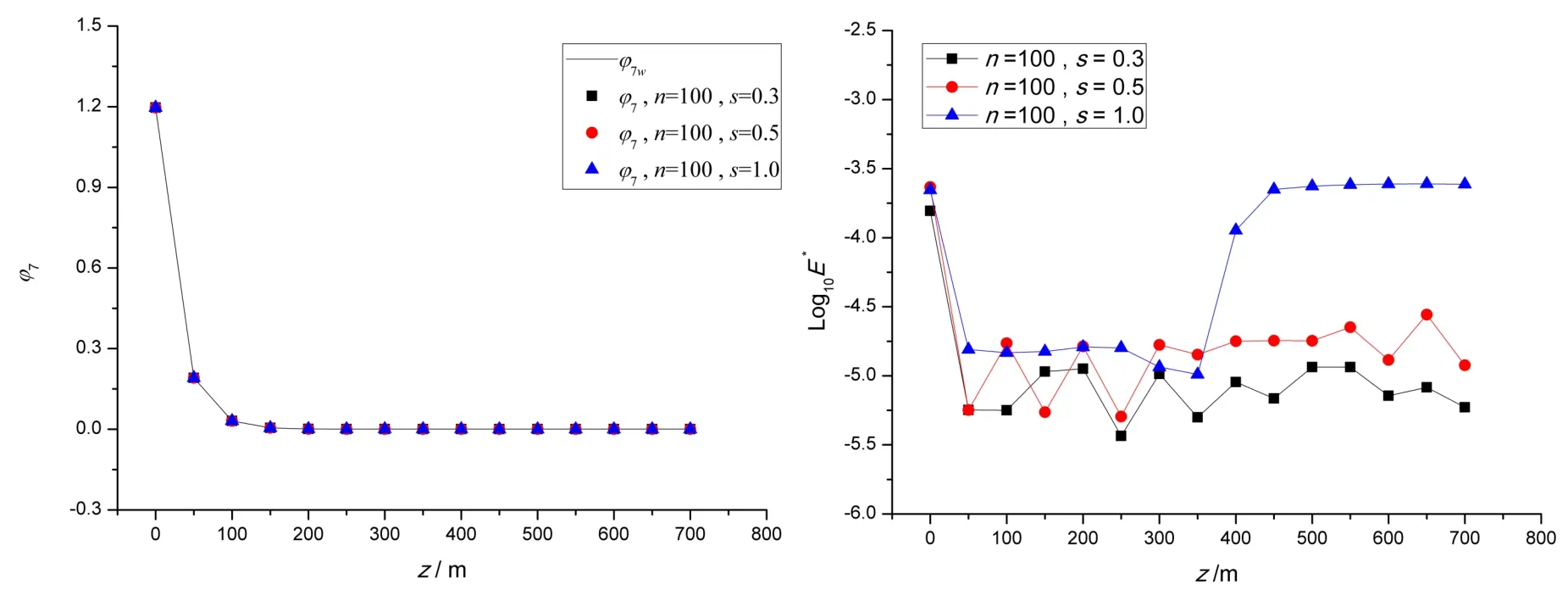
圖4 l1處繞射勢逼近值（實部）與絕對誤差（ω=0.6 rad/s）Fig.4 Diffracted approximation(real part)and absolute error along l1(ω=0.6 rad/s)

圖5 l1處繞射勢逼近值（虛部）與絕對誤差（ω=0.6 rad/s）Fig.5 Diffracted approximation(imaginary part)and absolute error along l1(ω=0.6 rad/s)

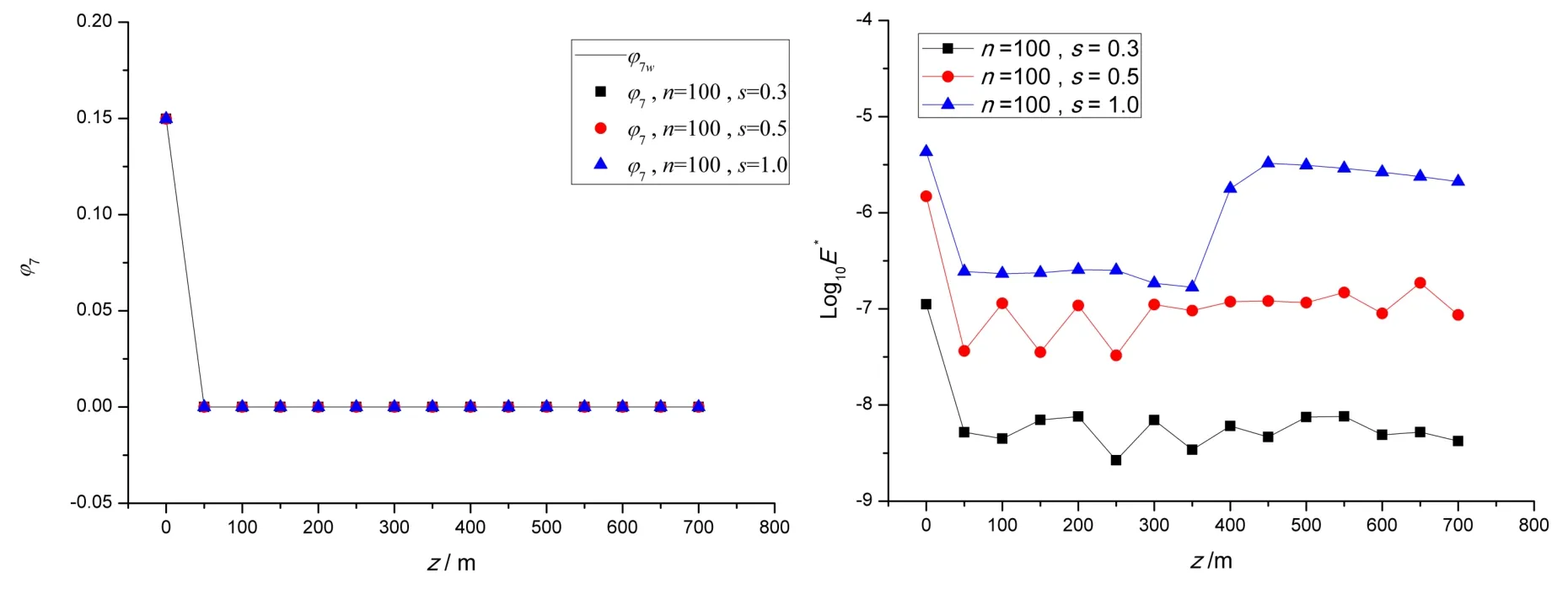
圖6 l1處繞射勢逼近值（實部）與絕對誤差（ω=1.7 rad/s）Fig.6 Diffracted approximation(real part)and absolute error along l1(ω=1.7 rad/s)

圖7 l1處繞射勢逼近值（虛部）與絕對誤差（ω=1.7 rad/s）Fig.7 Diffracted approximation(imaginary part)and absolute error along l1(ω=1.7 rad/s)

4 結 論

文中定義了含有伸縮系數s的Laguerre函數，利用該函數，并且對一條FPSO在圓柱控制面的繞射勢進行數值逼近，得到以下結論：

（1）伸縮系數s增加了Laguerre函數的靈活性，并對Laguerre函數逼近連續衰減函數的收斂性進行了證明。

（2）Gauss-Legendre與Gauss-Laguerre結合的積分方法可以提高函數積分精度，對震蕩衰減的函數也可以得到較好積分結果。

（3）當波浪頻率較低時，繞射勢沿水深衰減較慢，此時伸縮系數s=0.3可以得到較好逼近效果；波浪頻率較高時繞射勢沿水深衰減較快，任意不同伸縮系數都可以得到較好結果。文中為了得到較高精度級數展開項較多，工程應用中，在滿足工程應用精度情況下，可以減少展開項數，提高運算效率。

[1]戴遺山,段文洋.船舶在波浪中的勢流理論[M].北京:國防工業出版社,2008:107-219. Dai Yishan,Duan Wenyang.Potential flow theory of ship motions in waves[M].Beijing:National Defense Industry Press, 2008:107-219.

[2]戴仰山,沈進威,宋競正.船舶波浪載荷[M].北京:國防工業出版社,2007:23-37. Dai Yangshan,Shen Jinwei,Song Jingzheng.Ship wave loads[M].Beijing:National Defense Industry Press,2007: 23-37.

[3]賀五洲,戴遺山.簡單Green函數法求解三維水動力系數[J].中國造船,1986(2):3-17. He Wuzhou,Dai Yishan.Three-dimension hydrodynamic coefficients based on rankine source method[J].Shipbuilding of China,1986(2):3-17.

[4]劉應中,繆國平.船舶在波浪上的運動理論[M].上海:上海交通大學出版社,1987:81-110. Liu Yingzhong,Miao Guoping.The theory of ship motions in waves[M].Shanghai:Shanghai Jiao Tong University Press, 1987:81-110.

[5]Chen X B,Wu G X.On singular and highly oscillatory properties of the Green function for ship motions[J].J Fluid Mech, 2001,445:77-91.

[6]Ten I,Chen X B.A coupled Rankine-Green function method applied to the forward-speed seakeeping problem mathematical formulation[C]//IWWWFB 2010,International Workshop Water Waves Floating Bodies,25th.Harbin,China,issue 1,2010:4.

[7]張善杰,金建銘.特殊函數計算手冊[M].南京:南京大學出版社,2011:12-14. Zhang Shanjie,Jin Jianming.Computation of special functions[M].NanJing:Nanjing University Press,2011:12-14.

[8]Guo Benyu,Wang Zhongqing.Numerical integration based on Laguerre-Gauss interpolation[J].Comput.Methods.Appl. Mech.Engrg,2007:3726-3741.

Numerical approximation of diffraction waves on cylinder surface based on Laguerre function

LI Hui1,LV Ming-dong2,REN Hui-long1,CHEN Xiao-bo3,TIAN Bo1
(1.College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China;2.Marine Design&Research Institute of China,Shanghai 200011,China;3.Deepwater Technology Research Center,Bureau Veritas,Singapore)

The vertical variation of water diffraction waves on vertical infinite circular cylinder is considered to be continuous and descending.The variation can be represented by a series of Laguerre functions using Laguerre polynomials.A scale parameter s is introduced to the function which ensures orthogonality and flexibility.The convergence of Laguerre series is proved and diffraction wave of a FPSO on a circular cylinder surface is approximated for instance.The Gauss-Legendre integration is combined with Gauss-Laguerre integration to alternate traditional Gauss-Laguerre integration.This integration method can obtain higher numerical precision.The Laguerre series can be applied to approximate the velocity potential on the control surface in Rankine source method or Rankine-Kelvin source method.

Laguerre function;diffraction;Gauss-Laguerre integration;Gauss-Legendre integration

U661.3

：Adoi:10.3969/j.issn.1007-7294.2017.05.006

1007-7294（2017）05-0555-08

2016-12-29

國家基礎研究發展規劃項目（2011CB013703）

李 輝（1978-），男，講師，副博士生導師；呂明冬（1990-），男，助理工程師，E-mail：lvmingdong1990@qq.com。