正弦式交變電流有效值、平均值的推導與應用
■江蘇省如東高級中學 張 昡
正弦式交變電流有效值、平均值的推導與應用
■江蘇省如東高級中學 張 昡
一、正弦式交變電流的有效值
在交變電流變化的一個周期內,交變電流在電阻R上產生的熱量相當于一恒定電流在同樣時間內在該電阻上所產生的熱量,此恒定電流的數值就是該交變電流的有效值。
推導:設兩個正弦式交變電流的最大值和周期均相同,它們的瞬時值表達式分別為i1=Imaxs i nω t和i2=Imaxco sω t,其中現將它們分別加在兩個阻值均為R的電阻上,易知在一個周期內這兩個正弦式交變電流產生的焦耳熱Q相等。設這兩個正弦式交變電流的有效值為I,則Q=I2R T。在一個周期內,兩個正弦式交變電流產生的總焦耳熱Q總=2I2R T。在任一時刻t,這兩個電阻的熱功率分別為P1==(Imaxs i nω t)2R, P2==(Imaxco sω t)2R,這兩個電阻總的熱功率P總=P1+P2=(Imaxs i nω t)2R+(Imaxco sω t)2R=I2maxR(s i n2ω t+co s2ω t)=R。可見,P總是一定值,與時刻t無關,故Q總=P總T=I2maxR T。又有Q總=2I2R T,所以
二、正弦式交變電流的平均值
在交變電流變化的半個周期內,通過電路中導體橫截面的電荷量和一恒定電流在同樣時間內通過該電路中導體橫截面的電荷量相等時,此恒定電流的數值就稱為該交變電流在半個周期內的平均值。
推導:如圖1所示,單匝矩形線框abcd在磁感應強度大小為B的勻強磁場中,繞O O'軸以角速度ω勻速轉動,線框的面積為S,負載電阻為R。易知當該線框勻速轉動時在電阻R中產生正弦式交變電流。電流的最大值線框在勻速轉動半周的過程中,產生的平均感應電動勢,線框中磁通量的變化量ΔΦ=2B S,則負載電阻R中電流的平均值
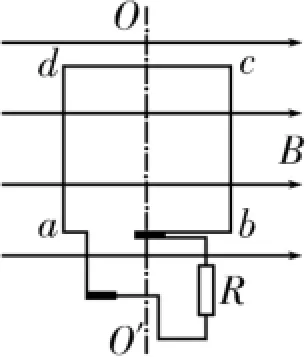
圖1
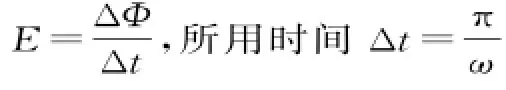
例題 如圖2所示,光滑絕緣水平桌面上直立一個單匝正方形導線框abcd,線框的邊長L=0.4m、總電阻R=0.1Ω。在直角坐標系x O y的第一象限中,有界勻強磁場區域的下邊界與x軸重合,上邊界滿足曲線方程m,磁感應強度大小B= 0.2T,方向垂直于紙面向里。線框在沿x軸正方向的拉力F作用下,以速度v=10m/s水平向右做勻速直線運動通過磁場區域。
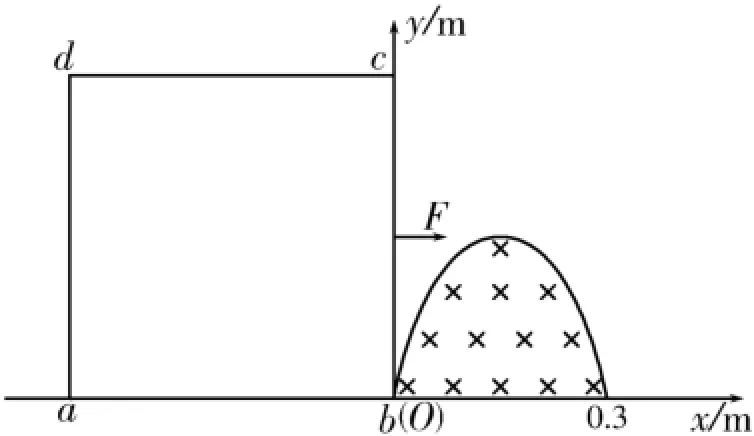
圖2
(1)畫出線框在運動過程中的電流i隨時間t變化的圖像。
(2)計算該磁場區域的面積S。
(3)求線框在穿越整個磁場的過程中,線框中產生的焦耳熱Q。
解:(1)如圖3所示,當線框的bc、ad邊運動到磁場中心線位置時,感應電動勢有最大值。
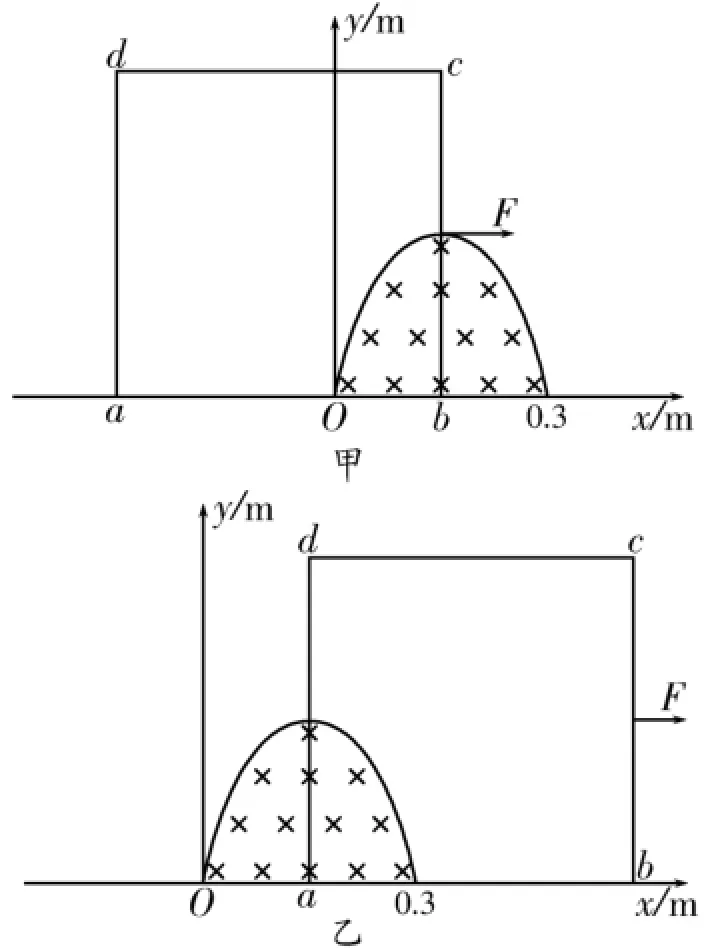
圖3
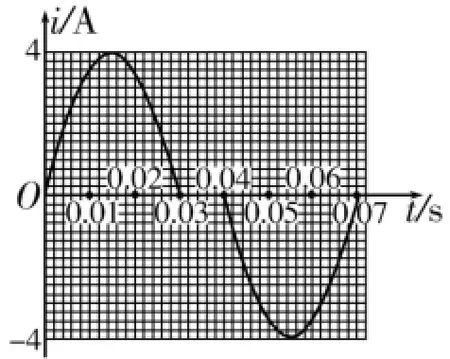
圖4
(2)t1時間內感應電流的平均值I=A,通過導線某一橫截面的電荷量C。t1時間內感應電動勢的平均值,線框中磁通量的變化量ΔΦ= B S,感應電流的平均值,通過導線某一橫截面的電荷量因此該磁場區域的面積
(3)在t1和t3時間內,線框中的感應電流按正弦規律變化,感應電流的有效值I=A,則線框中產生的焦耳熱Q= I2R(t1+t3)=0.048J。

圖5
如圖5所示,一固定的矩形導線框abcd水平放置,線框的左端接一只小燈泡L,在線框所在空間內存在與線框平面垂直的勻強磁場。已知線框的匝數n=100,電阻r=1Ω,所圍成矩形的面積S=0.04m2,小燈泡的電阻R=9Ω,磁感應強度按如圖6所示的規律變化,線框中產生的感應電動勢的瞬時值表達式為e=其中Bmax為磁感應強度的最大值,T為磁場變化的周期。不計燈絲電阻隨溫度的變化,求:
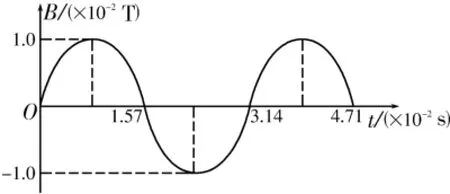
圖6
(1)線框中產生的感應電動勢的最大值。
(2)小燈泡消耗的電功率。
參考答案:(1)Emax=8V。(2)P= 2.88W。(3)Q=4×10-3C。
(責任編輯 張 巧)
- 中學生數理化(高中版.高二數學)的其它文章
- 有機化學專項訓練(三)
- 乙酸乙酯的制備要點透析
- 形形色色的傳感器問題
- 探究四種典型變壓器類型
- 淺談復數模的應用
- 例談一類雙變量不等式的證明

