基于結構降耦的一類低耦合度新型3T1R并聯機構的拓撲設計

沈惠平 強恒存 曾氫菲 孟慶梅 楊廷力

常州大學現代機構學研究中心,常州，213016

基于結構降耦的一類低耦合度新型3T1R并聯機構的拓撲設計

沈惠平 強恒存 曾氫菲 孟慶梅 楊廷力

常州大學現代機構學研究中心,常州，213016

四自由度的可實現SCARA型(三平移一轉動)輸出運動的并聯機構，與三自由度的Delta機構相比，因其本身的拓撲結構復雜，導致運動學正解以及動力學計算復雜，從而使其新機型的研究和開發應用相對困難;而降低這些機構的耦合度(簡稱結構降耦)可直接降低機構運動學、動力學求解的難度。根據筆者提出的機構結構降耦方法，對筆者最近提出的一類5個耦合度值κ為2且具有較好實用價值的SCARA型新型并聯機構進行了結構降耦優化，得到了耦合度較低(降為κ=1)但自由度和動平臺輸出運動類型均保持不變的10個SCARA新機型，而這10個低耦合度(κ=1)機構的運動學正解及動力學正反解，可用一維搜索法方便求得數值解，或從易導出的1個一元高次代數方程求得封閉解，為其進一步構型拓撲優化、設計及應用研究奠定了基礎。

結構降耦；拓撲結構優化；方位特征；運動學正解;耦合度

0 引言

SCARA(selective compliance assembly robot arm)串聯機械手由日本山梨大學牧野洋教授于1978年發明，它包括X、Y、Z方向的平動自由度和繞Z軸的轉動自由度(三平移一轉動，3T1R)，由于其Z軸具有良好的剛度，故特別適合裝配工作，已廣泛地用于電子產品、汽車、藥品及食品等領域[1]。ABB 公司于1999年開發出了基于三平移Delta(1985,Clavel)并聯機構(parallel mechanism， PM)的SCARA并聯操作手FlexPicker[2-3]，并得到廣泛應用；Pierrot及其團隊相繼發明了H4(1999年)、I4(2003年)、Par4系列(2005年)四自由度SCARA并聯操作手，并得到了較好的工業應用[4-6]。

國內對SCARA型并聯機構也進行了研究：趙鐵石等[7]提出了一種4-URU型三平移一轉動并聯機器人；金瓊等[8]基于單開鏈理論提出了一類三平移一轉動并聯機器人，并于2003年申請了一組5個具有單動平臺的三平移一轉動并聯機構[9]，但均未研制樣機；黃田等[10]開發了具有2個或者3個動平臺的四自由度三平移一轉動的Cross-IV型高速搬運機器人，并實現了產業化；劉辛軍等[11]在國內首次研發出具有1個動平臺的X4型并聯機器人樣機。由此可見，相對于三平移Delta操作手研究和應用相對成熟，新型三平移一轉動并聯機構的研究和應用亟待加強。

另一方面，機構位置正解的求解是并聯機構研究中最基礎的重要內容之一，它直接關乎機構的誤差分析、奇異性分析及動力學分析的難易，而這些又與機構耦合度κ的大小有關[12]。耦合度反映了機構各獨立回路運動學、動力學參數之間的關聯、依賴程度，κ值大小反映了機構運動學、動力學問題求解的復雜性，κ值越大，復雜度越高。但對于如何降低耦合度κ，目前研究得較少。

文獻[13-14]從并聯機構支鏈本身的拓撲結構以及支鏈在動靜平臺之間的拓撲布置兩方面，提出了并聯機構的3種降耦設計方法及其相應的例子，并將機構的拓撲結構降耦作為機構拓撲結構優化的主要內容和手段之一。

楊廷力等[15]提出了一類具有較好應用前景的13個四自由度的SCARA型(三平移一轉動)并聯機構，其中10種為新機構，它們能實現三平移和繞動平臺法線的一個轉動輸出，但這些機構的耦合度均較高(κ=2[15])，這是由其本身復雜的拓撲結構引起的，也意味著其運動學正解以及動力學計算比較復雜。因此，降低這些機構的耦合度(簡稱結構降耦)，對這類新型3T1R并聯機構的設計與應用具有重要意義。

本文根據筆者提出的機構結構降耦方法[13-14]，對文獻[15]中5種單平臺的新型并聯機構進行結構降耦，分別得到了動平臺具有3個、2個受力點的降耦機構各5個，它們保持了機構的基本功能——自由度和動平臺輸出運動不變，但耦合度均從κ=2降低為κ=1，從而使得這10個低耦合度機構的運動學正解及動力學正反解可用一維搜索法方便求得數值解，或從易導出的1個一元高次代數方程求得實數解。

1 耦合度及結構降耦方法

1.1 耦合度

以下給出單開鏈的約束度、機構耦合度κ的定義及其計算式，以及自由度F的計算公式[16]。

1.1.1 單開鏈的約束度

基本運動鏈(basic kinematic chain，BKC)中的第j個單開鏈(single-open-chain,SOC)的約束度定義為

(1)

式中，mj為第j個單開鏈的運動副數;fi為第i個運動副的自由度;Ij為第j個單開鏈的驅動副數;ξLj為第j個獨立回路的獨立位移方程數。

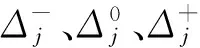
1.1.2 基本運動鏈的耦合度

基本運動鏈的耦合度定義為

(2)

并且，對于一個基本運動鏈，須有

式中，ν為獨立回路數。

min{?}指一個基本運動鏈分解為ν個單開鏈SOC(Δj)時，可有多種分解方案，應取∑|Δj|最小的單開鏈分解方案；而機構耦合度κ值為所含基本運動鏈中的最大耦合度。

1.1.3 機構自由度公式[16]

機構自由度公式為

(3)

式中，F為機構自由度；Mbj為第j條支路末端構件的方位特征(position and orientation characteristics， POC)集；dim{·}為POC集的維數。

1.2 結構降耦原理及其方法

由上文可知，機構的結構降耦設計(coupling-reducing design，CRD)就是降低機構的耦合度。由式(1)、式(2)知，BKC耦合度κ值的大小取決于基本回路的約束度(Δj)值大小，因此，降低機構單開鏈回路的約束度(Δj)值即可降低機構的耦合度κ值[13]。

文獻[13]介紹了基于設計混合支鏈的、基于運動副復合的、基于方位特征支鏈主動化的3種結構降耦設計方法。由于本文分析的5個新型SCARA機構[15](表1中A列類型Ⅲ～Ⅶ)均由轉動副和球副構成，因此，運動副復合法就是合并動平臺上的轉動副、球副(或減少動平臺的邊數)，以使式(1)中的自由度數fi減少，從而使Δj減小，進而減小κ，達到這5個SCARA機構結構降耦的目的。

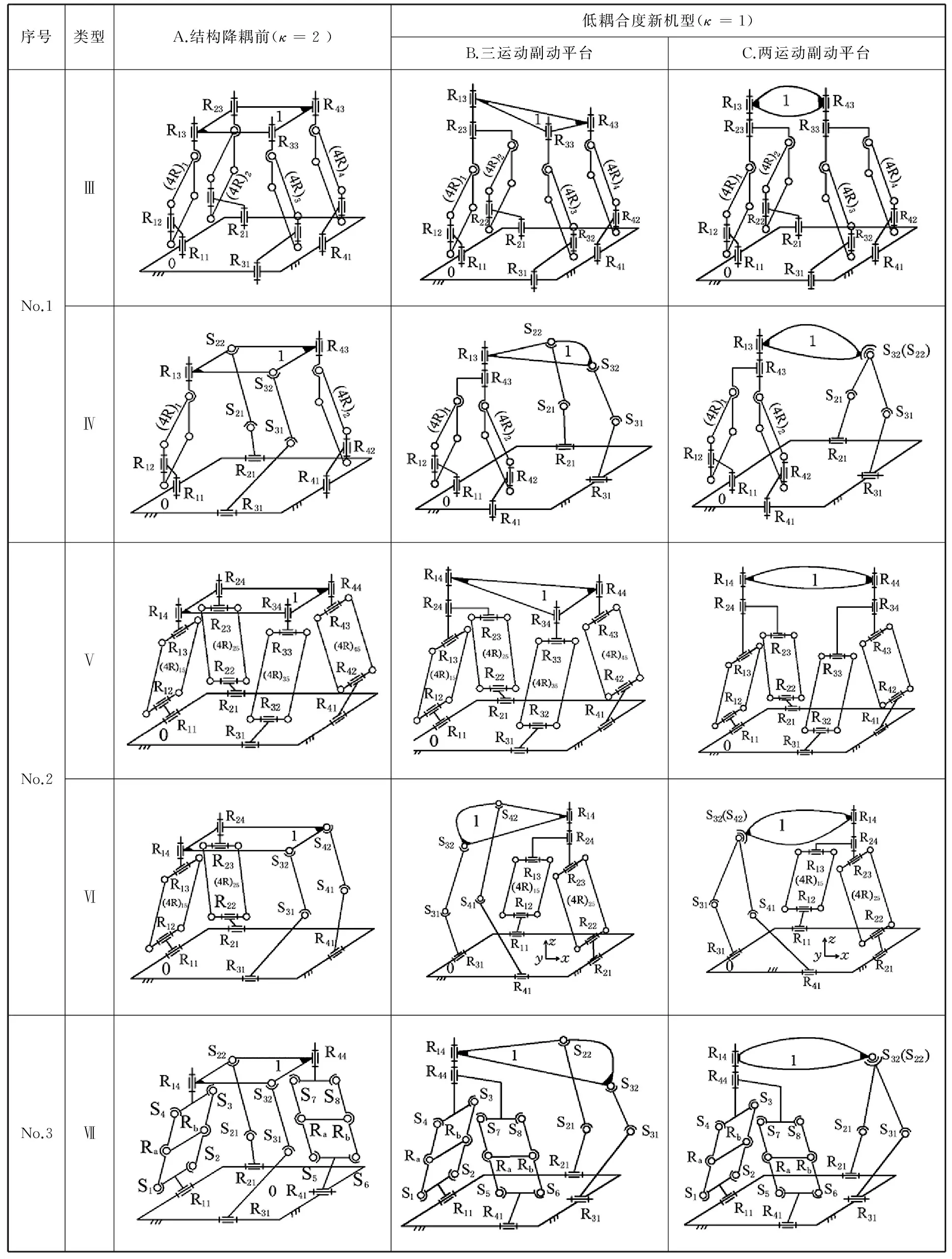
表1 新型3T1R并聯機構及其降耦設計后的拓撲結構

2 一類3T1R并聯機構的拓撲降耦設計

2.1 Ⅲ型3T1R機構的降耦設計和分析

2.1.1 Ⅲ型3T1R并聯機構

Ⅲ型3T1R并聯機構如圖1所示[15-17],由動平臺1、靜平臺0以及4條結構相同的復雜支鏈組成，即動平臺1上有4個受力點；每條支鏈都含有一個平面4R平行四邊形機構，表示為Ri1∥Ri2(-◇(4R)i-)∥Ri3(i=1,2,3,4)(其中，◇表示由4R組成的平行四邊形)。動平臺1上的4個轉動副R13、R23、R33、R43的軸線與動平臺的法線相互平行，也與靜平臺0上的4個轉動副R11、R21、R31、R41的軸線相互平行。

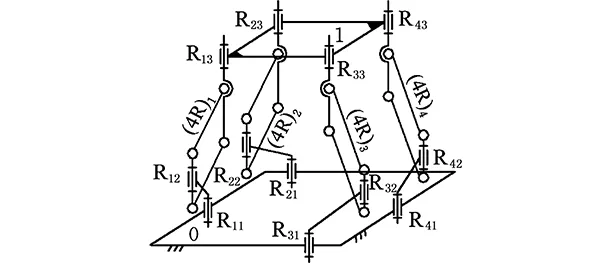
圖1 Ⅲ型3T1R并聯機構Fig.1 Ⅲ type 3T1R PM

易知，當轉動副R11、R21、R31、R41為驅動副時，動平臺1可實現三平移和繞動平臺法線的轉動輸出(取動平臺1任意一點O作為基點)；同時，該機構由1個基本運動鏈組成，且耦合度κ=2[15]，因此，其運動學正解及動力學正反解求解十分復雜(本文其余4個機構相同，不再贅述)。

2.1.2 Ⅲ型 3T1R并聯機構的降耦設計

將圖1所示機構動平臺1上的轉動副R13、R23的軸線重合，則成為圖2a所示的降耦機構[18](稱為一次降耦)，此時，動平臺1上有3個受力點。現計算其耦合度。

(1)取第1條單開鏈回路：

SOC1{-R11∥R12(-◇4R1-)∥R23∥

(-◇4R2-)R22∥R21-}

其獨立位移方程數

其中，t3表示三維移動；r1(∥R11)表示繞R11軸線有1個轉動。

則其約束度

同理，可求得ξL2=ξL3=4。

(2)第2條單開鏈及其約束度分別為

SOC2{-R31∥R32(-◇(4R3)-)∥R33-R13}

(3)第3條單開鏈及其約束度分別為

SOC3{-R41∥R42(-◇(4R4)-)∥R43}

由式(2)、式(3)，降耦機構的耦合度、自由度分別為

F=16-4-4-4=4

進一步，將圖2a機構動平臺1上的另外2個運動副R33、R43軸線復合(稱為二次降耦)，得到動平臺僅有2個受力點的新機型[19]，如圖2b所示；分析其耦合度時，3個單開鏈回路選擇與前述情況相同，因此，其約束度值Δj(j=1，2，3)也相同，二次降耦后的機構耦合度也是κ=1(為節省篇幅，以下4個機構二次降耦后的耦合度分析類似，不再贅述)。

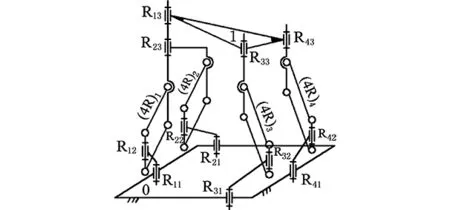
(a)一次降耦設計

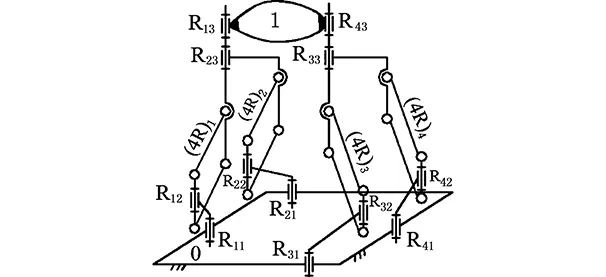
(b)二次降耦設計圖2 Ⅲ型3T1R并聯機構的降耦設計Fig.2 Coupling-reducing design(CRD) for Ⅲ type 3T1R PM

至此，代表機構基本功能的2個最主要拓撲特征——自由度F(仍為4)和方位特征(仍為3T1R)都不變，但2個降耦機構的運動學正解、動力學分析的難度大大降低了，其不同點在于動平臺分別為3個和2個受力點，這可能會影響動平臺1的工作靈活性及其工作空間大小，具體情況有待進一步分析。

2.2 Ⅳ型3T1R機構的降耦設計和分析

2.2.1 Ⅳ型3T1R并聯機構

同樣地，將圖1機構中的任兩條復雜支鏈用簡單無約束支鏈R-S-S替換，另外兩條復雜支鏈不變，則變成圖3所示的Ⅳ 3T1R型機構[17]，顯然，該機構的自由度數、方位特征與圖1機構相同，但耦合度仍為κ=2。

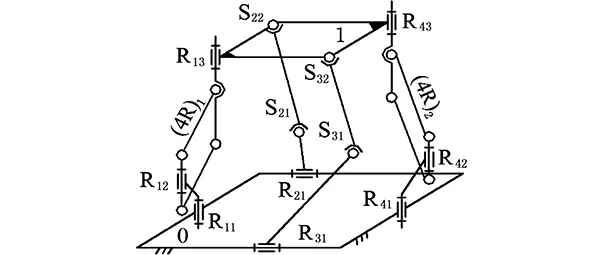
圖3 Ⅳ型3T1R并聯機構Fig.3 Ⅳ type 3T1R PM

2.2.2 Ⅳ型3T1R并聯機構的降耦設計

將圖3機構的動平臺1上的轉動副R13、R43軸線重合，則成為圖4a所示的動平臺1上有3個受力點的機構[18]，其耦合度計算如下。

(1)由2條復雜支鏈構成的第1回路

SOC1{-R11∥R12(-(◇4R)1-)∥

R43(-(◇4R)2-)∥R42∥R41-}

其獨立位移方程數和約束度分別為

(2)第2條支鏈形成的回路及其約束度分別為

SOC2{-R13-S22-S21-R21-}

(3)第3條支鏈形成的回路及其約束度分別為

SOC3{-S32-S31-R31-}

由式(2)、式(3)，該機構的耦合度、自由度分別為

F=20-4-6-6=4

進一步，將圖4a所示機構動平臺1上的球副S22、S32重合，得到二次降耦后的新機構，如圖4b所示，其動平臺1上僅有2個受力點；同理，可計算得到該機構的基本功能(POC集、F=4)不變，但耦合度由κ=2降為κ=1。

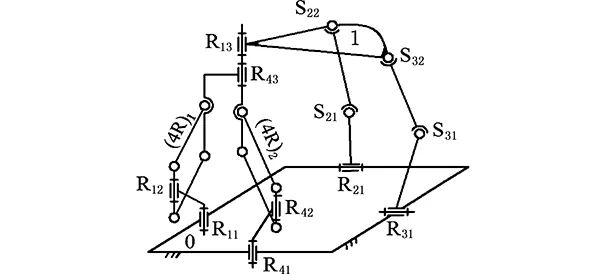
(a)一次降耦設計

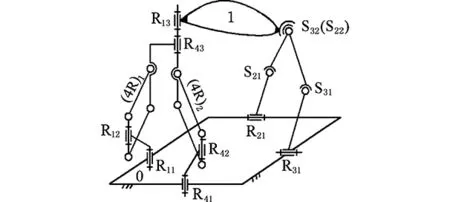
(b)二次降耦設計圖4 Ⅳ型3T1R并聯機構的降耦設計Fig.4 CRD for Ⅳ type 3T1R PM

2.3 Ⅴ型3T1R機構的拓撲降耦設計和分析

2.3.1 Ⅴ型3T1R并聯機構

如圖5所示，該機構由動平臺1、靜平臺0以及4條相同的復雜支鏈組成[15-20]，每條復雜支鏈都含有1個平面4R平行四邊形機構，表示為Ri1∥Ri2(-◇(4Ri5)-)∥Ri3⊥Ri4(i=1,2,3,4)。動平臺1上的轉動副R14、R24、R34、R44的軸線與動平臺1的法線平行，靜平臺0上的轉動副R11⊥R21及R31⊥R41，且為驅動副。

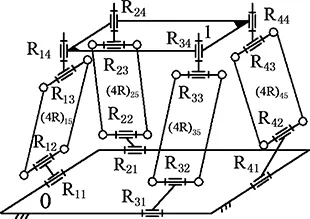
圖5 Ⅴ型3T1R并聯機構Fig.5 Ⅴ type 3T1R PM

2.3.2 Ⅴ型 3T1R并聯機構的降耦設計

將動平臺1上的轉動副R14、R24軸線重合，則構成圖6a所示的機構[21]，其耦合度計算如下。

(1)對于第1條單開鏈

SOC1{-R11∥R12(-◇(4R)15-)∥R13⊥R24⊥

R23(-◇(4R)25-)∥R22∥R21-}

其獨立位移方程數和約束度分別為

(2)第2條單開鏈及其約束度分別為

SOC2{-R14∥R34⊥R33(-◇(4R)35-)∥

R32∥R31-}

(3)第3條單開鏈及其約束度分別為

SOC3{-R44⊥R43(-(◇4R)45)∥R42∥R41-}

由式(2)、式(3)，降耦機構的耦合度、自由度分別為

F=20-6-5-5=4

進一步，將圖6a動平臺1上的轉動副R44、S34的軸線重合，得到二次降耦后的新機構[22]，如圖6b所示；同理計算其耦合度κ=1。這樣，在機構的基本功能(POC集、自由度)都不變的前提下，得到的2個并聯機構的耦合度均由κ=2降為κ=1。

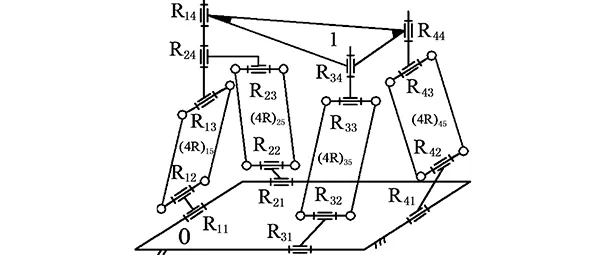
(a)一次降耦設計

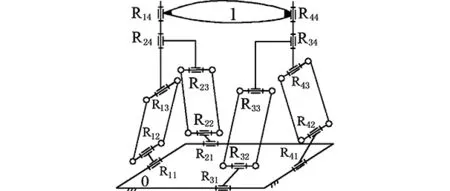
(b)二次降耦設計圖6 Ⅴ型3T1R并聯機構的降耦設計Fig.6 CRD for Ⅴ type 3T1R PM

2.4 Ⅵ型3T1R機構的拓撲降耦設計和分析

2.4.1 Ⅵ型3T1R并聯機構

將圖5機構靜平臺0上任一對轉動副軸線垂直的2條復雜支鏈用2條簡單支鏈R-S-S替換，即變成圖7所示的Ⅵ型 3T1R機構[20]，顯然，它們具有與圖5機構相同的自由度(F=4)、方位特征以及耦合度(κ=2)。下面對Ⅵ型3T1R機構進行降耦設計。

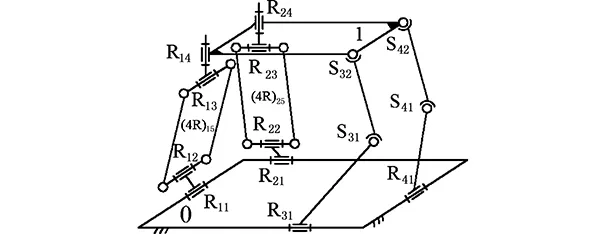
圖7 Ⅵ型3T1R并聯機構Fig.7 Ⅵ type 3T1R PM

2.4.2 Ⅵ型3T1R并聯機構的降耦設計

將圖7所示的機構動平臺1上的轉動副R14、R24軸線重合，則成為圖8a所示的機構[21]，其耦合度計算如下。

(1)第1條支鏈回路的獨立位移方程數及其約束度分別為

SOC1{-R11∥R12(-(4R)15-)∥R13⊥R24⊥ R23( -(∥4R)25-)∥R22∥R21-}

(2)第2條單開鏈及其約束度分別為

SOC2{R14-S42-S41-R41-}

(3)第3條單開鏈及其約束度分別為

SOC3{-S32-S31-R31-}

由式(2)、式(3)，降耦機構的耦合度、自由度分別為

F=22-6-6-6=4

進一步，將圖8a機構動平臺1上的球副S23、S33重合，則得到圖8b所示的二次降耦機構[22]；同理，計算出其耦合度κ=1，而機構的POC集和自由度(F=4)都不變。

2.5 Ⅶ型3T1R機構的拓撲降耦設計和分析

2.5.1 Ⅶ型3T1R并聯機構

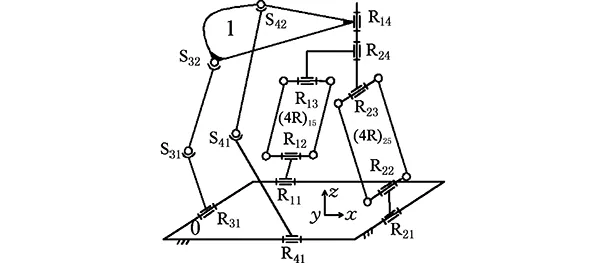
(a)一次降耦設計

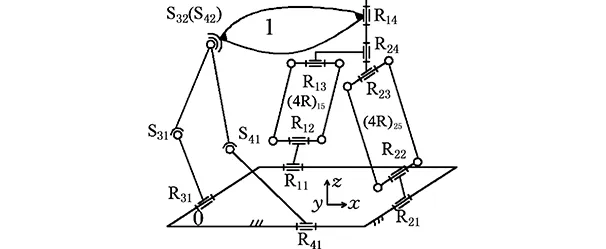
(b)二次降耦設計圖8 Ⅵ型3T1R并聯機構的降耦設計Fig.8 CRD for Ⅵ type 3T1R PM

Ⅶ型機構如圖9所示，它由動平臺1、靜平臺0、2條R-S-S型無約束支鏈，以及2條包含由4個球副組成的平行四邊形的混合支鏈組成[23]；裝配時，為使4個球副S1、S2、S3、S4的球心構成平行四邊形，必須在平行四邊形中配置一桿帶有兩轉動副(Ra、Rb)的結構，這樣可消去其沿平行四邊形對角線的一個轉動；動平臺1上的轉動副R14、R24的軸線須平行于動平臺1平面的法線；靜平臺0上的4個轉動副R11、R41、R31、R21為驅動副，但R11⊥R41。

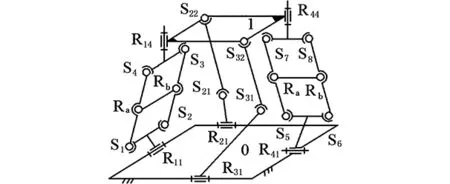
圖9 Ⅶ型3T1R并聯機構Fig.9 Ⅶ type 3T1R PM

2.5.2 Ⅶ型 3T1R并聯機構的降耦設計

將圖9機構動平臺1上的轉動副R14、R44軸線重合，則得圖10a所示機構[24]，其耦合度計算如下。

(1)第1支鏈回路的獨立位移方程數、約束度分別為

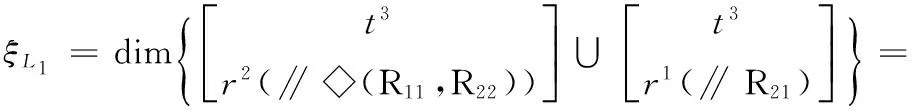
(2)第2支鏈及其約束度分別為

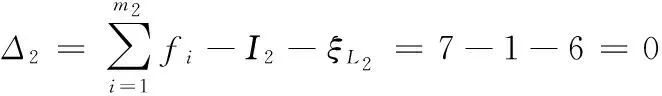
(3)第3支鏈及其約束度分別為

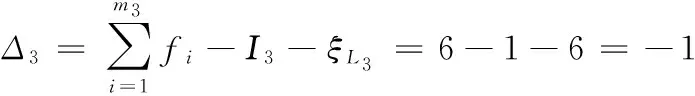
由式(2)、式(3)，降耦機構的耦合度、自由度分別為

F=22-6-6-6=4

進一步，將圖10a機構動平臺1上的球副S22、S32重合，則得到二次降耦后的新機構[24]，如圖10b所示；同理，計算得到新機構的耦合度κ=1，而機構的基本功能(方位特征和自由度)不變。

(a)一次降耦設計

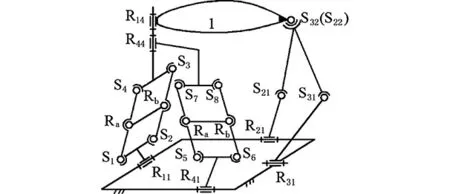
(b)二次降耦設計圖10 Ⅶ型3T1R并聯機構的降耦設計Fig.10 CRD for Ⅶ type 3T1R PM

至此，已對5個新型的3T1R并聯機構，通過其動平臺上的轉動副、球副重合，進行了結構降耦設計。表1給出了這5種機構結構降耦前后的結構對照，其中，A列為降耦前的5個原始機構(κ=2)；B、C列為相應的降耦后的動平臺分別具有3個受力點、2個受力點的低耦合度的5個機構(κ=1)，這10個新機構的位置正解、動力學正反解可用一維搜索法[25]方便求得數值解，或從易導出的1個一元高次代數方程中求得封閉解。

需要說明的是，表1中A列的5個機構(κ=2)是根據基于方位特征和單開鏈的并聯機構拓撲結構設計理論方法綜合而得，當然也可以運用螺旋理論等理論方法綜合而得，但無論用哪一種方法綜合(這些方法均包含支鏈設計、支鏈組合、支鏈在動靜平臺的幾何布置等3個步驟)，其耦合度值均較大，為κ=2。但表1中B列、C列的10個機構很難直接從這些方法綜合得到，這說明對由理論方法綜合而得的機構進行降耦設計，可以產生機構基本功能不變但耦合度更低的新機型，因此，結構降耦設計既可視為現有并聯機構拓撲結構優化的內容之一，又可認為是低耦合度并聯機構設計的一種新型實用方法，這是本文的主要創新點所在。

這樣，5個耦合度較大(κ=2)以及10個低耦合度(κ=1)的四自由度3T1R新機構均可實現三平移一轉動輸出，構成了可實現SCARA運動的機構庫，為其進一步研究、優選、設計與應用奠定了良好的理論基礎。

3 結論

(1)耦合度描述機構拓撲結構的復雜程度，它反映了機構回路內運動學、動力學參數的相互關聯依賴關系，耦合度越大，機構越復雜；結構降耦是機構拓撲結構優化設計的重要內容和手段之一，也是低耦合度并聯機構設計的一種新型實用方法。

(2)將動平臺上的轉動副或球副進行重合，可以使并聯機構的耦合度降低。

(3)5個原始3T1R并聯機構的耦合度為2，而本文提出的10個低耦合度(κ=1)的新機構，其運動學正解、動力學正反解易用一維搜索法方便求得數值解，或可從易導出的1個一元高次代數方程求得封閉解，還可使機構的結構設計、制造變得簡單，這對機構的應用具有重要意義。

[1] 袁山.SCARA機器人——依然快捷和可靠[J].機器人技術與應用，2005(5):31-33.YUANShan.SCARARobot—StillFastandReliable[J].RobotTechniqueandApplication,2005(5):31-33.

[2]CLAVELR.DevicefortheMovementandPositioningofanElementinSpace：US，4976582[P]. 1990-12-11.

[3]ABB.IRB360Flexpicker[EB/OL]. [2015-05-06].http： //www.new.abb.com/products/robotics/industrials-robots/irb-360.

[4]PIERROTF，COMPANYO.H4：aNewFamilyof4-dofParallelRobots[C]//ProceedingsoftheIEEE/ASMEInternationalConferenceonAdvancedIntelligentMechatronics，Atlanta.NewYork：IEEE，1999：508-513.

[5]KRUTS，COMPANYO，BENOITM，etal.I4：aNewParallelMechanismforSCARAMotions[C]//ProceedingsoftheIEEEInternationalConferenceonRoboticsandAutomation.Taipei：IEEE，2003：1875-1880.

[6]NABATV，COMPANYO，KRUTS，etal.Part4：VeryHighSpeedParallelRobotforPick-and-place[C]//ProceedingsoftheIEEE/RSJInternationalConferenceonIntelligentRobotsandSystems，Alberta.NewYork：IEEE，2005：1202-1207.

[7] 趙鐵石,黃真.欠秩空間并聯機器人輸入選取的理論和應用[J]. 機械工程學報，2000，36(10)：81-85.ZHAOTieshi,HUANGZhen.TheoryandApplicationofSelectingActuatingComponentsofSpatialParallelMechanisms[J].ChineseJournalofMechanicalEngineering, 2000, 36(10): 81-85.

[8] 金瓊，楊廷力，劉安心，等.基于單開鏈單元的三平移一轉動并聯機器人機構型綜合及機構分類[J]. 中國機械工程，2001，12(9)：1038-1043.JINQiong,YANGTingli,LIUAnxin,etal.KinematicsAnalysisofaParallelPneumaticandHydraulicLinkageBasedonSingle-opened-chain[J].ChinaMechanicalEngineering, 2001, 12(9): 1038-1043.

[9] 楊廷力，金瓊，羅玉峰，等. 用于虛軸機床與機器人等的一類(三平移一轉動)并聯機構：中國，200310106012.4[P].2003-10-18.YANGTingli,JINQiong，LUOYufeng，etal.AClassof3T1RParallelMechanismsUsedforVirtualAxisMachineToolsandRobots：China，200310106012.4[P]. 2003-10-18.

[10] 黃田，劉海濤，李曚. 五自由度機器人：中國，CN1709657[P]. 2005-7-11HUANGTian，LIUHaitao，LIMeng.TheRobotwithFiveDegreeofFreedom：China,CN1709657[P].2005-7-11.

[11] 劉辛軍，謝福貴，王立平，等. 一種可實現SCARA運動的四自由度單動平臺并聯機構：中國，201210435375.1[P]. 2012-11-02.LIUXinjun，XIEFugui，WANGLiping，etal.AFourFreedomofDegreeParallelMechanismwithSingleMovingPlatformWhichCanAchieveScaraMove:China，201210435375.1[P]. 2012-11-02.

[12]YANGTL.StructuralAnalysisandNumberSynthesisofSpatialMechanisms[C]//Proc.ofthe6thWorldCong.ontheTheoryofMachinesandMechanisms.NewDelhi，1983: 280-283.

[13]SHENHuiping，YANGLiangjie，MENGQingmei，etal.TopologicalStructureCoupling-reducingofParallelMechanisms[C]//2015IFToMMWoldCongress，2015,Taipei，China.DOI: 10.6567/IFToMM.14TH.WC.OS13.120.

[14] 沈惠平，朱小蓉，尹洪波，等.并聯機構的結構降耦原理及其設計方法[J]機械工程學報,2016,52(23):102-113.SHENHuiping，ZHUXiaorong，YINHongbo，etal.ThePrincipleandDesignMethodforStructureCoupling-reducingofParallelMechanisms[J].JournalofMechanicalEngineering，2016，52(23): 102-113.

[15]YANGTingli，LIUAnxin，SHENHuiping，etal.TopologicalStructureSynthesisof3T1RParallelMechanismBasedonPOCEquations[M]//IntelligentRoboticsandApplications.Berlin:SpringerInternationalPublishing, 2016：147-161.

[16] 楊廷力, 劉安心，羅玉峰，等.機器人機構拓撲結構設計[M].北京：科學出版社, 2012.YANGTingli，LIUAnxin，LUOYufeng，etal.TheoryandApplicationofRobotMechanismTopology[M].Beijing:ChinaSciencePress, 2012.

[17] 沈惠平，楊廷力，李菊，等，一種三平移一轉動并聯機器人裝置：中國，201510567133，1[P]. 2015-9-8.SHENHuiping,YANGTingli,LIJu,etal.AParallelRobotDevicewithThreeTranslationsandOneRotation:China, 201510567133.1[P].2015-9-8.

[18] 沈惠平，熊坤，楊廷力，等.一種低耦合度三運動副動平臺的三平移一轉動并聯機器人裝置：中國，201610141841.3[P]. 2016-03-12SHENHuiping,XIONGKun,YANGTingli,etal.ALowCouplingDegreeThree-translationandOne-rotationParallelRobotDevicewithaThree-jointMovingPlatform:China, 201610141841.3[P].2016-03-12.

[19] 沈惠平,曾氫菲,強恒存,等.一種低耦合度兩運動副動平臺的三平移一轉動并聯機器人裝置：中國，201610141696.9 [P]. 2016-03-12.SHENHuiping,ZENGQingfei,QIANGHengcun,etal.ALowCouplingDegreeThree-translationandOne-rotationParallelRobotDevicewithaTwo-jointMovingPlatform:China, 201610141696.9 [P].2016-03-12.

[20] 沈惠平，楊廷力，鄧嘉鳴，等.一種三平移一轉動并聯機器人機構：中國，201510566039.4[P].2015-9-8.SHENHuiping,YANGTingli,DENGJiaming,etal.AParallelRobotMechanismwithThreeTranslationsandOneRotation:China, 201510566039.4[P].2015-9-8.

[21] 沈惠平,強恒存,邵國為,等.一種低耦合度三運動副動平臺的三平移一轉動并聯機器人機構：中國，201610141468.1[P]. 2016-03-12.SHENHuiping,QIANGHengcun,SHAOGuowei,etal.ALowCouplingDegreeThree-translationandOne-rotationParallelRobotMechanismwithaThree-jointMovingPlatform:China, 201610141468.1[P].2016-03-12.

[22] 孟慶梅,沈惠平,邵國為,等.一種低耦合度兩運動副動平臺的三平移一轉動并聯機器人機構：中國，201610141831.X[P]. 2016-03-12.MENGQingmei,SHENHuiping,SHAOGuowei,etal.ALowCouplingDegreeThree-translationandOne-rotationParallelRobotDevicewithaTwo-jointMovingPlatform:China, 201610141831.X[P].2016-03-12.

[23] 沈惠平，楊廷力，朱偉，等.一種三平移一轉動并聯機器人平臺：中國，201510566840. 9[P]. 2015-9-8.SHENHuiping,YANGTingli,ZHUWei,etal.AParallelRobotPlatformwithThreeTranslationsandOneRotation:China, 201510566840. 9 [P]. 2015-9-8.

[24] 李菊,沈惠平,強恒存,等.一種低耦合度三運動副動平臺的三平移一轉動并聯機器人平臺：中國，201610141614.0[P]. 2016-03-12.LIJu,SHENHuiping,QIANGHengcun,etal.ALowCouplingDegreeThree-translationandOne-rotationParallelRobotPlatformwithaThree-jointMovingPlatform:China, 201610141614.0[P].2016-03-12.

[25]SHENHP，TingKL,YangTL.ConfigurationAnalysisofComplexMultiloopLinkagesandManipulators[J].MechanismandMachineTheory，2000, 35(3): 353-362.

(編輯 蘇衛國)

Topological Design for a Class of Novel 3T1R Parallel Mechanisms with Low Coupling Degree Based on Coupling-Reducing

SHEN Huiping QIANG Hengcun ZENG Qingfei MENG Qingmei YANG Tingli

Research Center for Advanced Mechanism Theory，University of Changzhou,Changzhou,Jiangsu,213016

Comparing to the 3-DOF Delta mechanism, the 4-DOF parallel mechanisms which might achieve selective compliance assembly robot arm(SCARA ) motion (i.e., three translations and one rotation) had their own complex topological structures, which resulted in the complexity of solutions for forward kinematics and dynamics. Therefore, the researches and developments of novel SCARA parallel mechanisms were still open issues. Reducing coupling degrees of these mechanisms might directly reduce the difficulties of solutions for forward kinematics and dynamics of the mechanisms. Based on the methods for structure coupling-reducing proposed by the authors, the structure coupling-reducing optimization design for five novel practical SCARA mechanisms whose coupling degreeκwere 2 proposed by authors was performed. Ten novel SCARA mechanisms with coupling degreeκ=1 were obtained, both their degrees of freedom and the output motion type of the moving platform kept to be constant. Thus, the solutions for forward kinematics and dynamics of these ten novel mechanisms with coupling degreeκ=1 might be easily obtained by using one dimensional search method, or by solving a one-variable polynomial equation derived. This paper provides a theoretical basis for topological optimization, design and applications for these novel SCARA mechanisms.

structure coupling-reducing; topological structure optimization; position and orientation characteristics; forward kinematics； coupling degree

2016-04-26

江蘇省重點研發計劃資助項目(BE2015043);國家自然科學基金資助項目(51375062，51475050)

TH112

10.3969/j.issn.1004-132X.2017.10.005

沈惠平，男，1965年生。常州大學機械工程學院教授、博士研究生導師。主要研究方向為機構學、并聯機器人、機械設計。獲江蘇省、教育部科技進步二等獎2項。發表論文190余篇。授權發明專利65項。E-mail:shp65@126.com。強恒存，男，1990年生。常州大學機械工程學院碩士研究生。曾氫菲，女，1993年生。常州大學機械工程學院碩士研究生。孟慶梅，女，1973年生。常州大學機械工程學院副教授。楊廷力，男，1940年生。常州大學機械工程學院特聘教授。