全斷面隧道掘進機刀盤裂紋尖端應力強度因子收斂性分析

凌靜秀 孫 偉 楊曉靜 童 昕

1.福建工程學院機械與汽車工程學院,福州，350118 2.大連理工大學機械工程學院，大連，116024

全斷面隧道掘進機刀盤裂紋尖端應力強度因子收斂性分析

凌靜秀1孫 偉2楊曉靜1童 昕1

1.福建工程學院機械與汽車工程學院,福州，350118 2.大連理工大學機械工程學院，大連，116024

針對全斷面隧道掘進機刀盤裂紋損傷及壽命預測等工程問題，提出了基于子模型技術的應力強度因子求解方法，并用含裂紋的矩形鋼板對該方法進行了驗證，分析了裂紋網格參數對刀盤裂紋尖端應力強度因子的收斂性影響。結果表明，鋼板的應力強度因子數值和理論計算結果最大相對誤差為3.6%。同時得到了保證刀盤應力強度因子求解精度和效率的裂紋單元網格參數，為結構的裂紋擴展壽命預測提供了參考。

全斷面隧道掘進機刀盤；裂紋；應力強度因子；子模型技術；有限元法

0 引言

全斷面隧道掘進機(tunnel boring machine，TBM) 是利用回轉刀具開挖及破碎洞內圍巖來開鑿巖石隧道，形成完整隧道斷面的一種大型高端隧道工程裝備。刀盤作為TBM關鍵部件，與圍巖直接接觸，是支撐滾刀切削巖石的箱體結構。由于地質環境及掘進參數的多變性，整機在掘進過程中振動極其劇烈，導致刀盤盤體開裂、支撐結構大變形及主軸承失效等問題[1-2]。刀盤結構在加工、制造及裝配過程中，不可避免地存在初始缺陷。這些初始缺陷會演化為疲勞破壞的裂紋源，在破巖載荷作用下裂紋不斷擴展，直至臨界尺寸，導致結構破壞，失去服役能力，因此，確定初始裂紋擴展到失效尺寸的時間，即預測刀盤的裂紋擴展壽命、合理評估含表面裂紋刀盤的抗斷裂能力顯得極為重要。

在進行結構斷裂分析時，應力強度因子是其中一個重要指標，是判斷裂紋擴展規律和驅動裂紋擴展的關鍵參數。應力強度因子求解方法可歸結為理論計算和試驗兩類方法，而理論方法包括解析法和數值法。解析法只能計算相對簡單的模型；數值法包含有限元法(FEM)、有限差分法(FDM)及邊界配置法(BGNP)等。解析法受到很多限制，數值法則在斷裂力學中得到廣泛的應用[3]。在用有限元法計算應力強度因子時，裂紋網格參數會對結果有一定的影響，需要合理選擇網格參數，進而得到穩定、準確的數值解。

在刀盤載荷及系統設計方面，相關學者已開展了大量的研究工作，且取得了一定的研究成果。謝啟江等[4]通過建立刀盤、機械系統和撐靴接觸剛度耦合力傳遞模型，研究了刀盤載荷波動與巖石接觸界面剛度的耦合關系。韓美東等[5]、夏毅敏等[6]采用ABAQUS 有限元軟件模擬刀盤掘進破碎巖石的過程，分析了刀盤載荷變化規律及不同參數對其統計值的影響，并用工程實際值進行了驗證。霍軍周等[7]建立了帶復雜性能約束的刀具布置優化模型，并用工程案例進行了驗證。另外，文獻[8-10]采用集中參數質量法、多體動力學仿真法及現場實測等手段對TBM刀盤系統的振動特性展開研究，分析了掘進參數、結構參數等不同參數對刀盤振動的影響，并與實測振動數據進行對比，來驗證理論動力學模型的有效性。

關于刀盤結構損傷的研究國內外基本處于空白，筆者基于系統動力學及有限元法分析了不同參數對刀盤裂紋應力強度因子的影響，提出了適用長厚板在復雜應力狀態下的新型失效判據準則，并預測了刀盤的裂紋擴展壽命[2,11]，但沒有分析裂紋網格參數對刀盤應力強度因子的影響，僅采用默認參數進行研究。本文以遼西北引水工程TBM刀盤為研究對象，采用奇異單元對刀盤分體結構裂紋尖端附近區域進行精細網格劃分，應用基于子模型技術的有限元方法直接計算刀盤裂紋尖端的應力強度因子，分析裂紋網格參數對應力強度因子收斂性的影響，進而確定較為穩定可靠的裂紋奇異單元網格參數。

1 應力強度因子求解方法及有效性驗證

1.1 應力強度因子求解方法

數值方法能夠求解復雜結構的三維應力強度因子，而有限元法中的奇異單元法是數值方法中求解應力強度因子適用面最廣的一種方法。構件中任意三維裂紋及尖端坐標系可抽象成圖1所示坐標系。

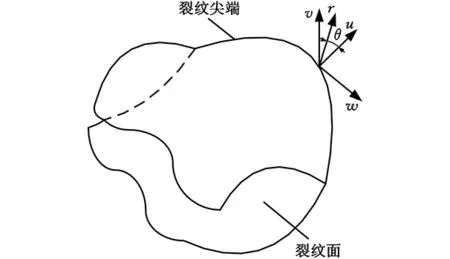
圖1 裂紋尖端局部坐標系Fig.1 Local coordinate system of crack tip

根據線彈性斷裂力學的解析解，由任意外載作用所產生的裂紋尖端附近區域的位移場和應力強度因子的關系可表示如下[12]：

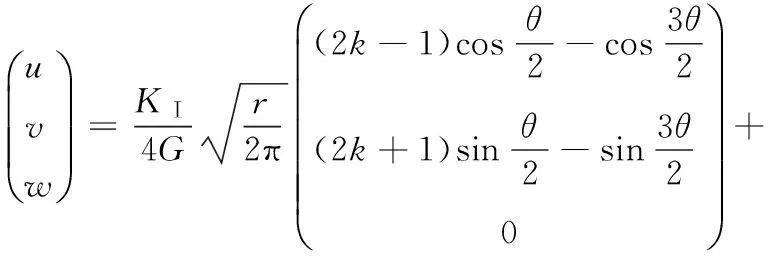
(1)

其中，r、θ為局部柱坐標系中的兩個坐標分量；u、v、w分別為裂紋尖端任一點的徑向位移、法向位移和切向位移；KⅠ、KⅡ、KⅢ分別為Ⅰ型、Ⅱ型及Ⅲ型應力強度因子；G為剪切模量；k為與材料泊松比μ有關的常數，對于平面應變問題，k=3-4μ，而對于平面應力問題，k=(3-λμ)/(1+μ)。

對于平面應變狀態，Ⅰ型裂紋的應力強度因子KⅠ可用裂紋面的法向位移表示，即

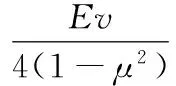
(2)

式中，E為彈性模量。

有限元軟件ANSYS中提供了一種求解三維裂紋問題的奇異單元，如圖2所示。裂紋尖端大部分區域處于平面應變狀態，在求得應力應變解后，取裂紋尖端1/4節點的裂紋張開位移v(1/4)代替尖端位移，代入式(2)中即可求得應力強度因子[12]：

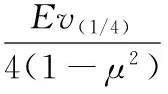
(3)

式中，r(1/4)為1/4節點到裂紋尖端的距離。

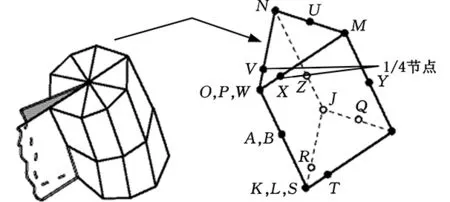
圖2 ANSYS提供的三維奇異單元Fig.2 Three dimensional singular element provided by ANSYS

1.2 本方法的有效性驗證

采用上述有限元子模型及計算方法，可方便快捷地求解出刀盤分體表面裂紋的應力強度因子，但計算結果是否正確，需要進行驗證和分析。然而，對于這類復雜結構的三維表面裂紋問題，目前沒有切實可行的驗證方法，因此，本文以中心部位含有半橢圓型三維表面裂紋的矩形鋼板為例，兩端承受均勻拉應力σt=100 MPa，如圖3所示。圖中，鋼板長度L=45 mm，寬W=70 mm，厚T=8 mm；裂紋長半軸c=4 mm，短半軸a=2 mm，θ為裂紋離心角。用ANSYS軟件求解該類裂紋問題的應力強度因子，同時采用工程界廣泛認可的Newman-Raju經驗公式計算[13]，二者對比，以檢驗本文奇異單元法的可靠性。

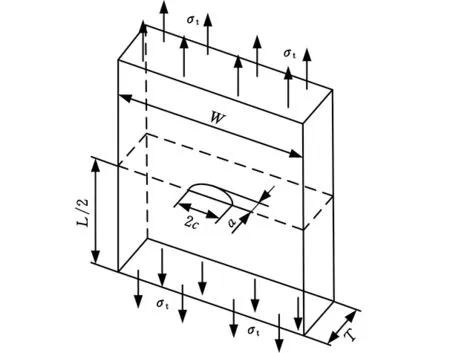
(a)含表面裂紋的鋼板

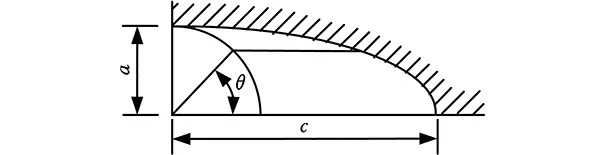
(b)裂紋離心角圖3 含表面裂紋鋼板的力學模型Fig.3 Mechanical model of steel plate with a surface crack

采用四面體單元劃分鋼板整體網格，裂紋區域引入奇異單元，模擬裂紋尖端應力場的奇異性，設置合適的裂紋網格參數，建立有限元模型，如圖4所示。在鋼板一端施加拉應力，一端固定，等效兩端受拉情況，載荷及邊界條件見圖3。裂紋尖端橢圓曲線共劃分為60份，含60組單元和61個節點，每個節點對應一個離心角，可得到61個應力強度因子。裂紋尖端徑向劃分為6層單元，即裂紋尖端各節點可得到6個應力強度因子。一般來說，越靠近內層的計算結果波動越大，越靠近外層的值則趨于穩定。為保證求解精度，程序默認每個裂紋尖端節點從最內層開始，會依次輸出6個應力強度因子值，本文選取最外層的值作為數值計算結果，提取結果如圖5所示。

(a)網格劃分(b)載荷與邊界條件圖4 有限元分析模型Fig.4 Finite element analysis model

圖5 ANSYS應力強度因子計算結果Fig.5 Stress intensity factor results calculated by ANSYS

由計算結果可知，應力強度因子基本呈現左右對稱的趨勢，即裂紋最深處應力強度因子最大，兩個表面點的值相對較小，這和實際情況相符。因此，采用Newman-Raju公式計算時，僅計算裂紋離心角θ在0～90°的應力強度因子值K1，并與數值計算結果進行比較，結果如圖6所示。

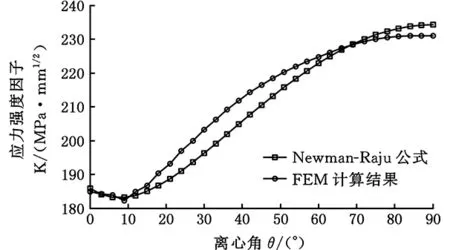
圖6 有限元與Newman-Raju公式計算結果對比Fig.6 Comparison of calculation results between FEM and Newman-Raju formula

由以上對比結果可知，總體而言，有限元結果與Newman-Raju公式的計算結果基本相符，最大相對誤差為3.6%，在工程允許的計算誤差范圍內，結果較符合實際。有限元計算結果與經驗公式結果在裂紋表面點處基本重合，隨著離心角的增大，有限元結果逐漸大于經驗公式結果，然后二者又慢慢接近，靠近裂紋尖端最深處區域時，經驗公式結果又稍微大些，這些計算結果的誤差變化很小，基本可以忽略。這說明按照本文的有限元方法，應用ANSYS軟件對刀盤分體三維表面裂紋的應力強度因子進行分析,理論上是可行的。

2 刀盤分體有限元模型

基于上述有限元子模型技術，合理等效刀盤分體結構，刪除滾刀、焊縫等細小結構，分割出裂紋子模型結構，利用ANSYS軟件對其進行網格劃分，采用四面體單元劃分裂紋子模型，奇異單元表征裂紋尖端的奇異性，分體其余實體結構采用六面體單元劃分。同時經過嚴格控制整體網格大小和裂紋尖端的網格參數，精細劃分刀盤分體結構，提高求解效率和精度。建立含半橢圓型三維表面裂紋的刀盤分體有限元模型，如圖7所示，同時加載刀盤載荷及位移邊界約束[2]。

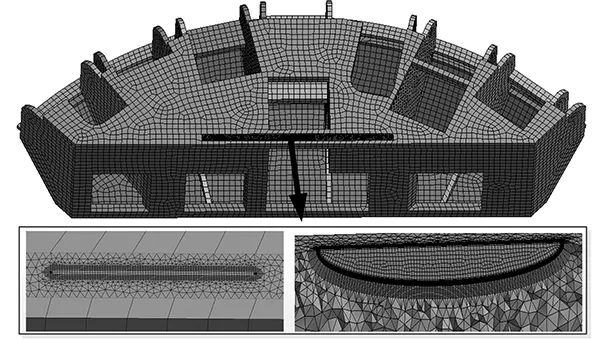
圖7 含裂紋特征的刀盤分體有限元模型[2]Fig.7 FEM model of cutterhead piece with crack[2]

3 裂紋網格參數對應力強度因子的影響

在上述有限元模型的基礎上，即可求出不同載荷作用下的應力強度因子值，但裂紋尖端附近的網格參數變化會對結果有所影響，已有研究針對不同問題提出了相應的裂紋網格參數選擇要求[13-14]。由此，需要結合刀盤有限元模型及實際載荷邊界，通過收斂性檢驗確定出合適的裂紋網格參數。ANSYS中裂紋尖端區域的網格參數如圖8所示，本文主要分析裂紋尖端周向網格份數nC、裂紋尖端徑向網格份數nM、最大輪廓半徑Ltip及裂紋尖端曲線網格份數nCF這四個裂紋網格控制參數的變化對刀盤裂紋尖端應力強度因子的影響。

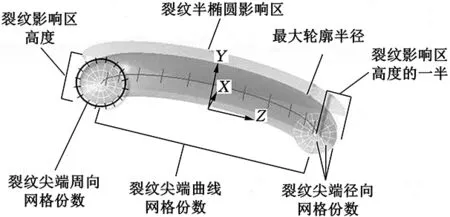
圖8 裂紋尖端區域的網格參數Fig.8 Mesh parameters in the crack tip region

3.1 周向網格份數

在圖7所示的有限元模型中，取裂紋短半軸a=30 mm，長半軸c=150 mm。在裂紋網格參數nM=6，Ltip=10,nCF=100的情況下，分析裂紋尖端周向網格份數分別為8、16、24、40時的應力強度因子分布，圖9所示為不同nC值對應的裂紋尖端區域的橫截面，計算得到不同nC值的應力強度因子值如圖10所示。

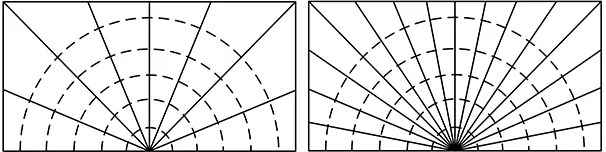
(a)nC=8 (b)nC=16

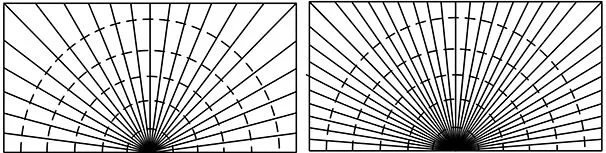
(c)nC=24 (d)nC=40圖9 不同nC值的裂紋尖端區域橫截面Fig.9 Cross sections of crack tip region with different nC values

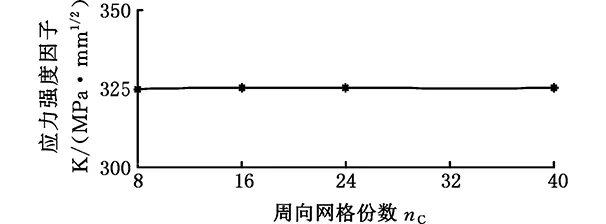
圖10 不同nC值時的應力強度因子Fig.10 Stress intensity factors with different nC values

由圖10可知，裂紋尖端周向網格份數的變化對應力強度因子幾乎沒有影響，隨著nC值的變化，計算結果最大幅度變化相對誤差在1%以內。為了提高求解效率，后續建立刀盤裂紋有限元模型時采用nC=8即可滿足精度要求。

3.2 裂紋尖端徑向網格份數

保持上述有限元模型及邊界條件不變，取nC=8，Ltip=10，nCF=100，分析裂紋尖端徑向網格數nM分別為6、8、10、20時的應力強度因子變化，不同nM值對應的裂紋尖端區域的橫截面如圖11所示。在第1譜級載荷幅值作用下，不同nM值的有限元模型計算得到的應力強度因子值如圖12所示。

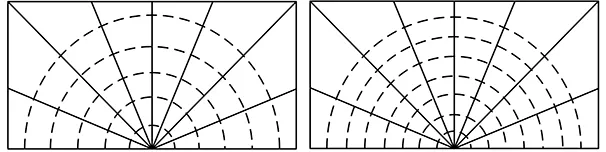
(a)nM=6 (b)nM=8

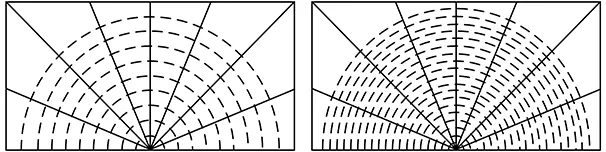
(c)nM=10 (d)nM=20圖11 不同nM值對應的裂紋尖端區域的橫截面Fig.11 Cross sections of crack tip region with different nM values

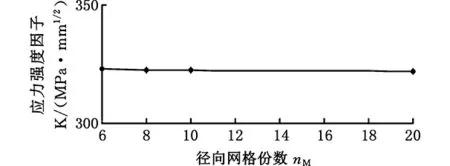
圖12 不同nM值對應的應力強度因子Fig.12 Stress intensity factors with different nM values

由圖12可知，裂紋尖端徑向網格份數的變化對應力強度因子的影響基本可以忽略，隨著nM值的變化，應力強度因子最大值與最小值之間相對誤差僅1.4%，在后續有限元建模時nM可取6～20之間的任意整數，本文取nM=8。

3.3 最大輪廓半徑

在ANSYS軟件中，裂紋尖端區域大小與裂紋的最大輪廓半徑成一定比例關系，程序會根據人為設定的最大輪廓半徑Ltip自動控制裂紋尖端區域的大小。同樣在以上模型的基礎上，取nC=8，nM=8，nCF=100，分析最大輪廓半徑Ltip分別為2、6、10、14、18時的應力強度因子變化，結果如圖13所示。

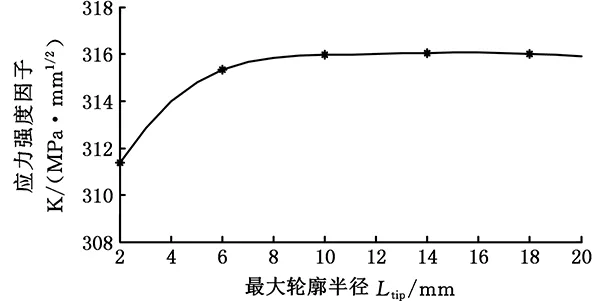
圖13 不同Ltip值對應的應力強度因子Fig.13 Stress intensity factors with different Ltip values

由圖13可知，裂紋的最大輪廓半徑變化對應力強度因子有一定的影響，而當Ltip值大于6時，計算結果幾乎保持不變，說明隨著Ltip的增大，應力強度因子逐漸趨于穩定。綜合考慮計算效率和求解精度，在后續有限元求解時可取Ltip=10。

3.4 曲線網格份數

同樣保持上述有限元模型不變，取nC=8，nM=8，Ltip=10，分析裂紋尖端曲線網格份數nCF分別為40、60、70、100時的應力強度因子變化，得到結果如圖14所示。

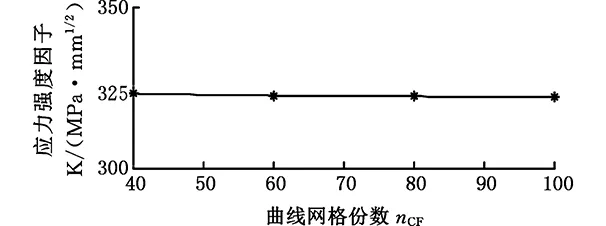
圖14 不同nCF值對應的應力強度因子Fig.14 Stress intensity factors with different nCF values

由圖14可知，裂紋尖端曲線網格份數的變化對應力強度因子影響很小，隨著nCF值的增大，應力強度因子最大值與最小值之間相對誤差僅1.2%，在后續有限元建模時nCF可取40～100之間的任意整數，本文取nCF=40即可滿足精度要求。

通過分析對比有限元模型中裂紋網格參數的變化對應力強度因子的影響可知，除裂紋的最大輪廓半徑外，其余裂紋網格參數對計算結果幾乎沒有影響。為保證后續分析結果的穩定可靠及提高計算效率，最終確定適合本文刀盤裂紋模型的網格參數如下：nC=8，nM=8，Ltip=10，nCF=40。

4 結論

(1)針對TBM刀盤的載荷特殊性及結構的復雜性，提出基于有限元子模型技術的裂紋應力強度因子求解方法，并用含裂紋的矩形鋼板進行驗證，得到數值和理論計算結果最大相對誤差為3.6%，在工程允許的誤差范圍內。

(2) 將提出的應力強度因子求解方法應用于實際引水工程的TBM刀盤結構裂紋，同時分析不同的裂紋網格參數對應力強度因子的影響，除裂紋的最大輪廓半徑外，其余參數對計算結果影響不大。

(3)通過分析得到了適用于求解實例刀盤應力強度因子的裂紋單元網格參數，為刀盤的裂紋擴展壽命預測提供了技術支撐。

[1] 黃文鵬.節理密集帶地質硬巖TBM刀盤損壞形式及對策[J].隧道建設,2012,32(4):587-593.HANGWenpeng.StudyonDamageofHardRockTBMInducedbyTunnelingthroughJoint-densely-developedHardRockSectionandCountermeasures[J].TunnelConstruction, 2012, 32(4):587-593.

[2]LINGJingxiu,SUNWei,HUOJunzhou,etal.StudyofTBMCutterheadFatigueCrackPropagationLifeBasedonMulti-degreeofFreedomCouplingSystemDynamics[J].Computers&IndustrialEngineering, 2015, 83:1-14.

[3] 衣振華.疲勞裂紋擴展研究及在裝載機橫梁壽命估算中的應用[D].濟南:山東大學，2011.YIZhenhua.ResearchonFatigueCrackPropagationandItsApplicationsinLoaderBeamLife[D].Jinan:ShandongUniversity, 2011.

[4] 謝啟江, 余海東. 硬巖掘進機刀盤載荷與撐靴接觸界面剛度的耦合關系[J]. 上海交通大學學報, 2015, 49(9):1269-1275.XIEQijiang,YUHaidong.CouplingRelationshipbetweenLoadsonCutterheadofTunnelBoringMachineandContactStiffnessofGripperShoesandRocks[J].JournalofShanghaiJiaotongUniversity, 2015, 49(9):1269-1275.

[5] 韓美東, 曲傳詠, 蔡宗熙,等. 刀盤掘進過程動態仿真[J]. 哈爾濱工程大學學報, 2015(8):1098-1102.HANMeidong，QUChuanyong，CAIZongxi,etal.DynamicNumericalSimulationofTunnelingbytheTBMCutterHead[J].JournalofHarbinEngineeringUniversity, 2015(8):1098-1102.

[6] 夏毅敏, 朱湘衡, 林賚貺,等.TBM刀盤掘進載荷影響因素研究[J]. 現代制造工程, 2015(9):1-6.XIAYimin，ZHUXiangheng，LINLaikuang,etal.AnalysisofInfluenceFactorsonLoadofTBMCutterhead[J].ModernManufacturingEngineering, 2015(9):1-6.

[7] 霍軍周, 史彥軍, 滕弘飛,等. 全斷面巖石掘進機刀具布置設計方法[J]. 中國機械工程, 2008, 19(15):1832-1836.HUOJunzhou,SHIYanjun,TENGHongfei,etal.CutterLayoutDesignofFull-faceRockTunnelBoringMachine(TBM) [J].ChinaMechanicalEngineering, 2008, 19(15):1832-1836.

[8]SUNWei,LINGJingxiu,HUOJunzhou,etal.DynamicCharacteristicsStudywithMultidegree-of-freedomCouplinginTBMCutterheadSystemBasedonComplexFactors[J].MathematicalProblemsinEngineering, 2013(3):657-675.

[9]HUOJunzhou,WUHangyang,YANGJing,etal.Multi-directionalCouplingDynamicCharacteristicsAnalysisofTBMCutterheadSystemBasedonTunnellingFieldTest[J].JournalofMechanicalScience&Technology, 2015, 29(8):3043-3058.

[10] 霍軍周, 歐陽湘宇, 王亞杰,等. 重載沖擊激勵下TBM刀盤振動特性的影響因素分析[J]. 哈爾濱工程大學學報, 2015(4):555-559.HUOJunzhou,OUYANGXiangyu,WANGYajie,etal.AnalysisofInfluencingFactorsofVibrationBehaviorsofTBMCutterheadunderHeavyImpactLoads[J].JournalofHarbinEngineeringUniversity, 2015(4):555-559.

[11]SUNWei,LINGJing,HUOJunzhou,etal.StudyofTBMCutterheadFatigueDamageMechanismsBasedonaSegmentedComprehensiveFailureCriterion[J].EngineeringFailureAnalysis, 2015, 58:64-82.

[12]LINXB,SMITHRA.FiniteElementModelingofFatigueCrackGrowthofSurfaceCrackedPlates—PartI:TheNumericalTechnique[J].EngineeringFractureMechanics, 1999, 63(5):503-522.

[13]NAMIMR.StressIntensityFactorsinaRotatingImpellerContainingSemi-ellipticalSurfaceCrack[J].MechanicsBasedDesignofStructuresandMachines, 2012, 40(1):1-18.

[14]CHIEWSP,LIEST,LEECK,etal.StressIntensityFactorsforaSurfaceCrackinaTubularT-joint[J].InternationalJournalofPressureVesselsandPiping, 2001, 78(10):677-685.

(編輯 王旻玥)

Convergence Analysis of Stress Intensity Factor at Crack Tips for TBM Cutterheads

LING Jingxiu1SUN Wei2YANG Xiaojing1TONG Xin1

1.School of Mechanical and Automotive Engineering,Fujian University of Technology,Fuzhou,350118 2.School of Mechanical Engineering,Dalian University of Technology,Dalian,Liaoning,116024

Aiming at the engineering problems such as crack damage and life prediction of TBM cutterheads, a solution method of stress intensity factors was proposed based on the sub-model technique, and it was validated by a rectangular steel plate with a crack. Then the convergence effects of crack mesh parameters on stress intensity factors at the crack tips of cutterheads were analyzed. The analysis results show that the maximum relative errors of numerical and theoretical results are as 3.6%. Besides, the crack element mesh parameters were obtained that ensured both of the accuracy and efficiency for cutterhead stress intensity factors solutions, which may provide a reference for the crack growth life prediction of structures.

tunnel boring machine(TBM) cutterhead; crack; stress intensity factor; sub-model technique; finite element method(FEM)

2016-06-28

國家重點基礎研究發展計劃(973計劃)資助項目(2013CB035402);福建省科技創新平臺建設項目(2014H2002)；福建省自然科學基金資助項目(2016J01722,2017J01675)；福建工程學院科研啟動基金資助項目(GY-Z160048)

TP391.9

10.3969/j.issn.1004-132X.2017.10.002

凌靜秀，男，1985年生。福建工程學院機械與汽車工程學院講師、博士。主要研究方向為復雜機械裝備動力學分析及疲勞壽命預測。E-mail：ljxyxj@fjut.edu.cn。孫 偉，男，1967年生。大連理工大學機械工程學院教授、博士研究生導師。楊曉靜，女，1985年生。福建工程學院機械與汽車工程學院助理實驗師。童 昕，男，1964年生。福建工程學院機械與汽車工程學院教授、博士研究生導師。