基于Allan方差解耦自適應濾波的旋轉SINS精對準方法

胡 杰，程向紅，朱倚嫻

（東南大學 微慣性儀表與先進導航技術教育部重點實驗室，南京 210096）

基于Allan方差解耦自適應濾波的旋轉SINS精對準方法

胡 杰，程向紅，朱倚嫻

（東南大學 微慣性儀表與先進導航技術教育部重點實驗室，南京 210096）

對旋轉式 SINS精對準方法進行了研究，由于轉位機構轉動干擾以及慣性器件誤差不確定性帶來的影響，旋轉式 SINS狀態方程和量測方程噪聲方差參數難以確定，進而導致初始對準精度降低，針對這個問題引入自適應Kalman濾波技術。Sage-Husa是一種常用的自適應濾波算法，但是存在噪聲參數強耦合缺陷。通過研究Allan方差與量測噪聲方差之間的關系，利用Allan方差濾波器具有帶通濾波的特點，獨立計算量測噪聲協方差陣Rk，該方法能夠有效克服Sage-Husa濾波耦合問題，相比其它改進方法具有簡單易實現等特點。對該研究進行了仿真實驗與實際系統驗證實驗，結果表明：對于中等精度光纖陀螺單軸旋轉SINS，自適應Kalman濾波算法航向角對準精度比標準Kalman濾波算法精度要高0.6′左右，且在誤差估計過程中，自適應Kalman濾波器能夠更好地抑制外界干擾誤差的影響，是一種較好的精對準方法。

旋轉式SINS；精對準；Allan方差；自適應Kalman濾波

旋轉式慣導系統通過周期性轉動慣性測量單元（Inertial Measurement Unit，IMU）能夠將慣性器件常值誤差對導航精度的影響予以抵消，達到誤差自補償的目的[1-2]。美國于20世紀70年代開始了此類系統的研究，先后研制出MK39Mod3C、AN/WSN-7B激光陀螺單軸旋轉捷聯慣導系統（SINS），MK49、AN/WSN-7A激光陀螺雙軸旋轉 SINS以及光纖陀螺三軸旋轉SINS等[3-5]。國內也有許多研究機構開展旋轉調制系統的研究工作，如國防科學技術大學、天津航海儀器研究所以及哈爾濱工程大學等[2,6-7]。

旋轉式 SINS一般應用于艦船等需要長時間工作的場合，初始對準精度對于后續導航精度的提高具有至關重要的意義。自對準技術不需要外界輔助信息，具有完全自主的優點，從而得到了廣泛應用。由于載體工作環境惡劣，比如艦船系泊在碼頭進行初始對準時會受到風浪等因素干擾，艦體會產生較大幅度搖晃，使得慣導系統自主對準濾波使用的量測值產生多種不確定性干擾。同時對于旋轉式 SINS而言，由于基座的連續轉動，其系統模型具有較強的動態變化過程，采用標準Kalman濾波進行初始對準，系統對準精度將會降低。為解決此問題，通常采用自適應濾波技術，在進行濾波的同時利用量測信息不斷估計和修正模型參數以提高濾波估計精度。文獻[8]在捷聯慣導系統初始對準時應用Sage-Husa自適應濾波算法估計系統模型和噪聲的統計特性，但Sage-Husa自適應濾波中參數之間是相互耦合和制約的，如果其中某處出現干擾偏差，就可能影響到其它環節并進一步相互影響，容易造成濾波器的不穩定；張濤[9]提出了一種新的模糊自適應組合導航信息融合算法，將指數加權應用到系統誤差和量測誤差的估計中，以達到避免濾波發散的目的，同時利用模糊邏輯方法確定指數參數，模糊自適應 Kalman濾波器的設計相對較為復雜。本文給出一種解耦自適應濾波在 SINS精對準中的應用方法，該方法利用 Allan方差分析法估計自適應濾波中的量測噪聲參數，消除了量測噪聲方差估計器與濾波方程之間的互相耦合。進行了數學仿真和轉臺驗證實驗，結果表明，本文所提出的自適應濾波方法具有更高的初始對準精度。

1 單軸旋轉調制原理

單軸旋轉SINS中IMU安裝在內部轉位機構上，假設該轉動坐標系為s系，即 oxsyszs，其相對載體坐標系（b系，oxbybzb）旋轉，使得水平方向上的 IMU常值誤差呈周期性變化，其余坐標系的假設與常規捷聯慣導系統一樣，分別為導航坐標系（n系，oxnynzn）和慣性坐標系（i系，oxiyizi）。

初始時刻s系與b系重合，系統通電后s系開始以角速度Ω繞 ozb軸轉動，兩者之間的夾角為Ωt，因此它們之間的轉移矩陣為

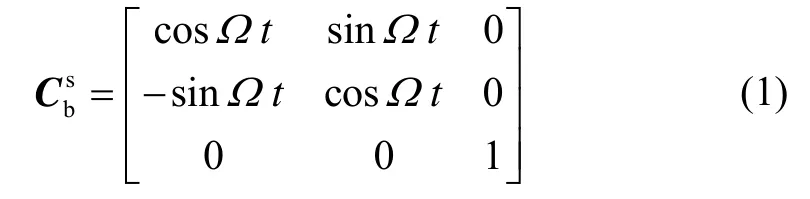
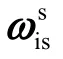
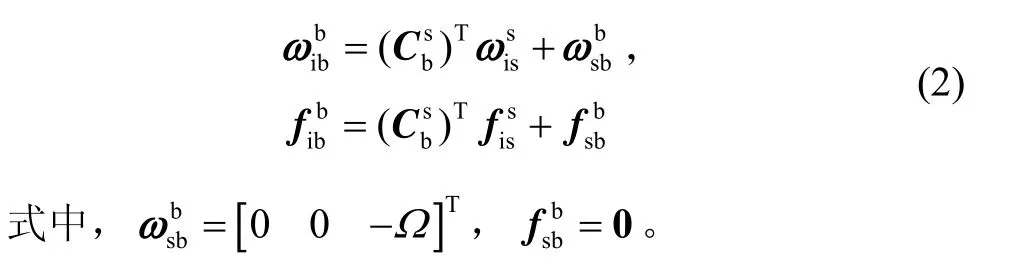
旋轉坐標系s中陀螺和加速度計信息可以寫成[10]：

將式(3)代入式(2)中可以得到：

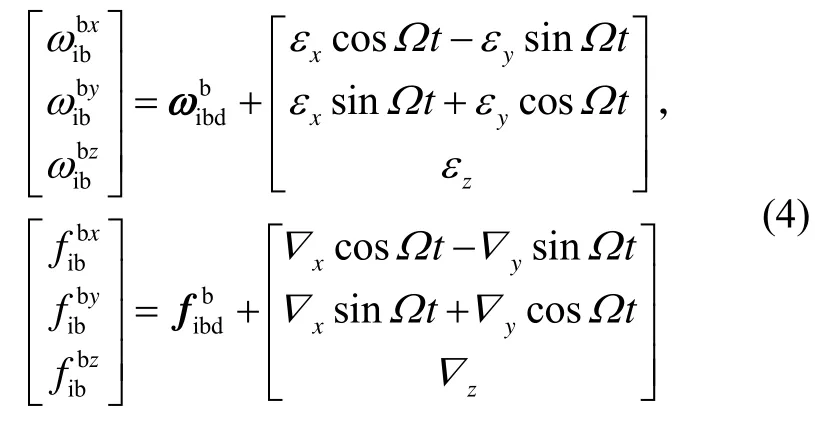
由式(4)可知，水平方向上的陀螺和加速度計常值誤差經過調制后變成周期性誤差量，一個周期內其誤差積分為零，單軸旋轉 SINS中沿轉軸方向上的慣性量誤差無法被調制，其對導航誤差的影響依然存在。

2 單軸旋轉SINS精對準模型

由于慣導系統垂直通道發散，在系統誤差狀態方程中將垂直方向上的誤差項忽略。在東北天坐標系建立初始對準誤差模型，取10個狀態向量，分別為水平速度誤差δvE、δvN，失準角φE、φN、φU，水平加速度計常值偏置?x、?y，陀螺常值漂移εx、εy、εz。根據系統誤差模型，狀態方程可以寫成如下形式[11]：

式中：X=[δvEδvNφEφNφU?x?yεxεyεz]T；W表示系統噪聲向量；

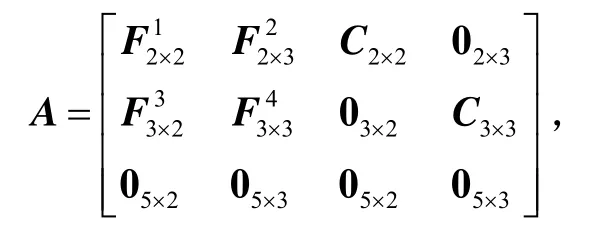
其中：

量測方程采用“速度+比力”匹配方式。選取兩個水平速度誤差δvE、δvN以及等效東向和北向加速度計輸出fE、fN作為觀測量。量測方程如下：

式中，V是系統量測噪聲矢量，此時系統的量測矩陣為

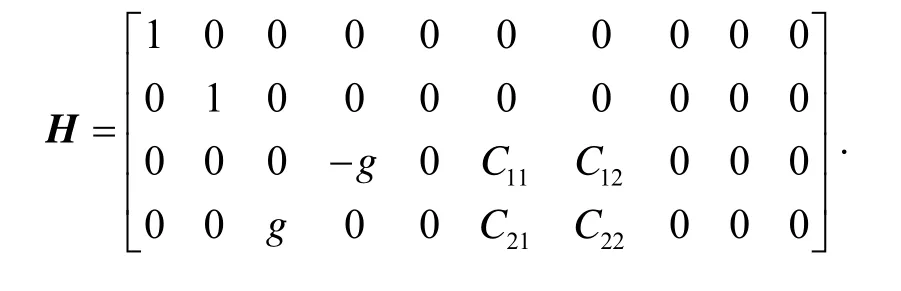
式(5)為以微分形式描述的連續性誤差方程。利用Kalman濾波算法進行遞推運算時需要首先對其進行離散化，式(7)為離散化后的狀態方程和量測方程：

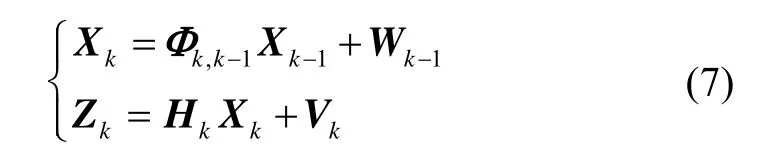
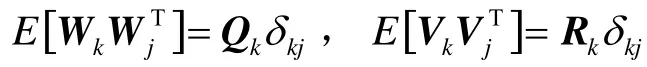
3 解耦自適應Kalman濾波算法

由于外界環境干擾以及基座的連續轉動，無法得到準確的系統噪聲和量測噪聲的統計特性，繼續使用標準 Kalman進行精對準則結果相對較差。目前Sage-Husa自適應卡爾曼濾波在導航系統初始對準領域得到廣泛應用，該方法針對系統激勵噪聲協方差陣Qk和量測噪聲協方差陣Rk未知或者近似已知的問題，利用量測信息由濾波器本身不斷地估計和修正噪聲統計特性。文獻[12]指出，自適應參數之間是互相耦合和制約的，如果其中某處出現干擾偏差，就可能影響到其他環節并進一步互相影響，最終導致濾波發散。針對這個問題，本文提出一種基于 Allan方差的量測噪聲方差估計的解耦自適應Kalman濾波方法。

3.1 量測噪聲方差的在線估計

若從頻域角度分析，量測噪聲主要表現為寬帶噪聲，而系統噪聲主要為低頻噪聲，因此通過對量測輸出的頻帶分割就有可能分離出量測噪聲參數。20世紀60年代美國國家標準局研究員David Allan首次提出Allan方差分析法，該方法可廣泛應用于任何精密測量儀器的隨機誤差分析。Allan方差濾波器是帶通濾波器，可以直接濾除大部分低頻噪聲，而對于寬帶白噪聲，其 Allan方差恰好等于白噪聲的方差，因此這里采用Allan方差估計量測噪聲方差：

在實際應用中，通常認為量測噪聲向量的各個分量之間是不相關的。對量測向量的每一個分量進行Allan方差分析，一般只需計算取樣間隔為最短采樣時間τ0時的Allan方差，將Allan方差的估計公式寫成如下遞推形式：

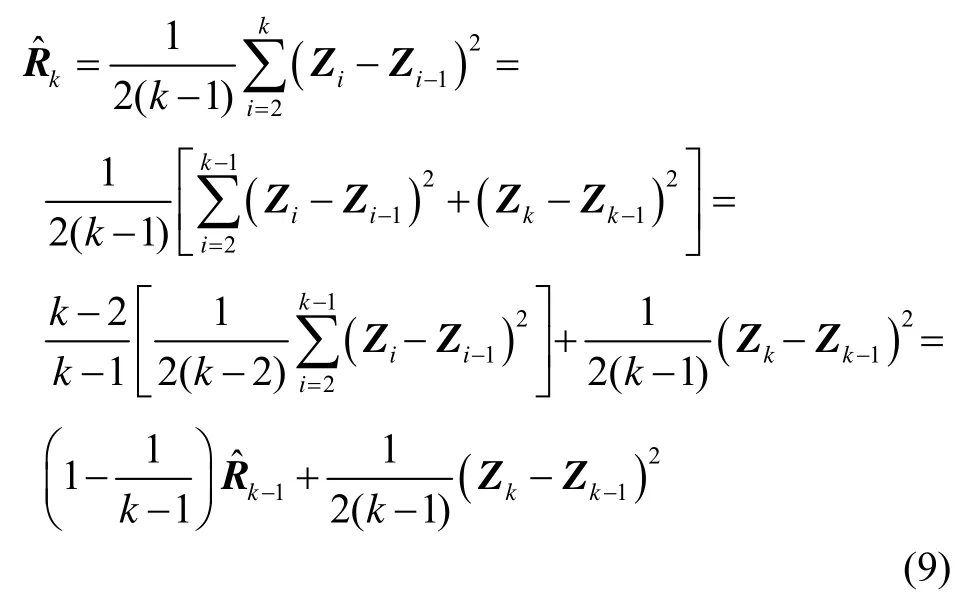
為了增強當前信息的權重，采用漸消記憶算法進行估計，則有：

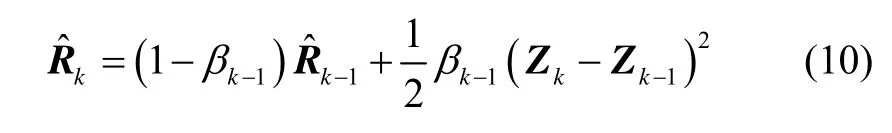
式(10)為基于 Allan方差的量測噪聲方差自適應算法，在該方法中量測噪聲方差的估計過程與Kalman濾波過程互相獨立，采用Allan方差進行噪聲自適應估計能夠有效降低Kalman濾波發散的風險。

3.2 解耦自適應Kalman濾波算法

在Sage-Husa自適應濾波框架中，采用Allan方差分析法估計量測噪聲的方差參數，由此可以構建得到解耦自適應Kalman濾波方程：

在旋轉式 SINS初始對準中，采用解耦自適應濾波器進行誤差估計時可以有效提高慣導系統對準精度以及環境適應能力。

4 仿真實驗與分析

假設三個陀螺的常值漂移均為0.01 (°)/h，隨機游走系數為0.005 (°)/h1/2，標度因數誤差為10×10-6，陀螺組件六個安裝誤差角為 10″；三個加速度計的零偏均為0.2 mg，隨機噪聲標準差為0.1 mg，標度因數誤差為10×10-6，加速度計組件的6個安裝誤差角為10″；轉位機構測角精度為5″。

由于單軸旋轉 SINS基座的連續轉停運動，其相對常規 SINS的初始對準具有更大的動態變化過程。圖1為兩種方法精對準姿態角誤差對比曲線，由圖1可知，當采用自適應濾波器進行初始對準時，姿態和航向角收斂更穩定，且具有更高的精度。表1為精對準結束后姿態角誤差對比值，由表1可知，15 min精對準濾波補償后，采用自適應濾波時，航向角誤差為0.29′，而標準Kalman濾波算法航向角誤差為1.73′，標準 Kalman濾波水平姿態角收斂結果同樣也差于本文所提出的自適應濾波結果。

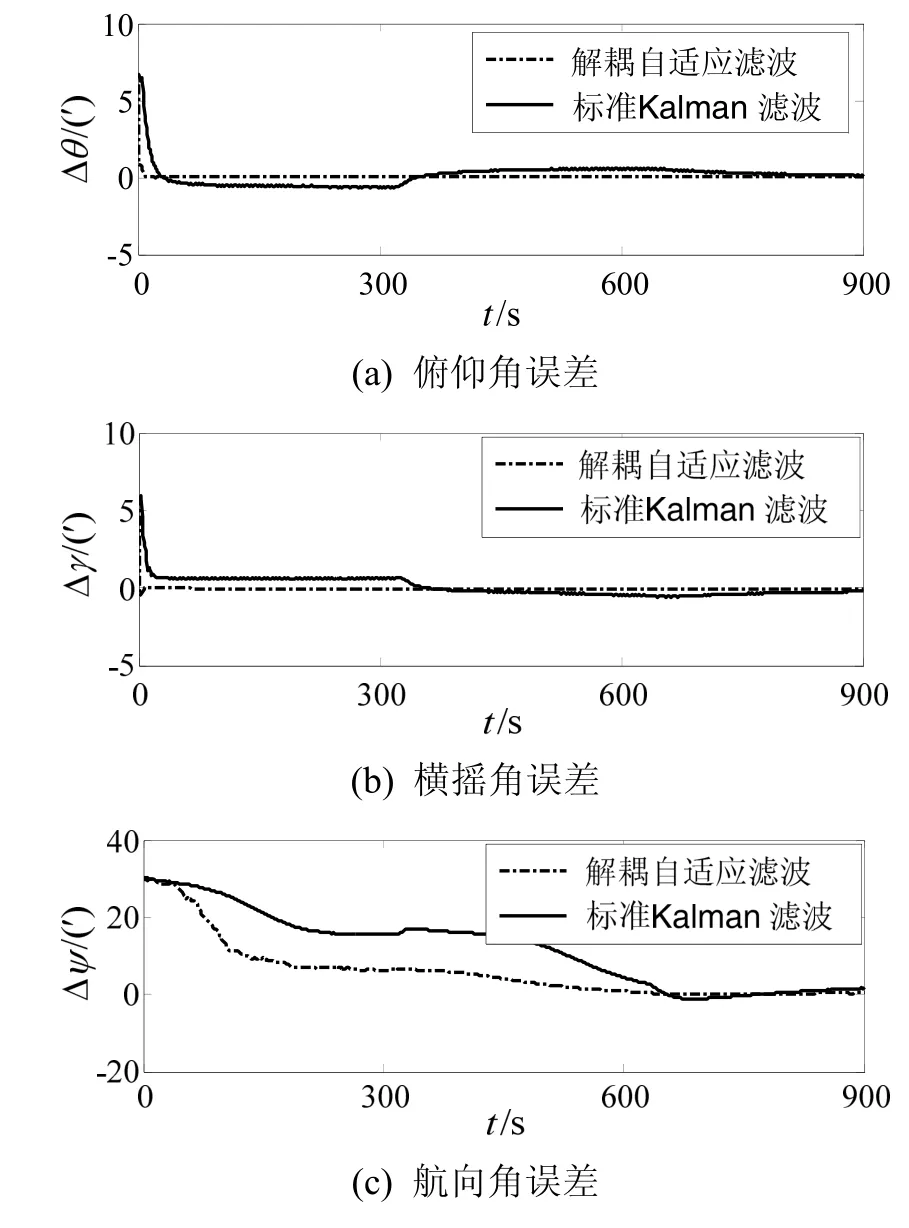
圖1 精對準姿態角誤差曲線Fig.1 Attitude error curves of refined alignments

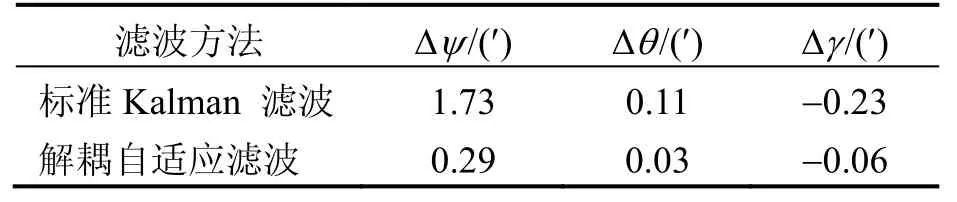
表1 兩種濾波方法初始對準結果Tab.1 Initial alignment results of the two methods

5 旋轉式SINS精對準實際系統驗證

為進一步驗證本文所提出的濾波方法的實際性能，采用三軸慣性測量轉臺與自行研制的光纖陀螺單軸旋轉SINS搭建實驗平臺（如圖2所示），進行了兩種對準方法的實驗比較，其中，光纖陀螺與加速度計參數指標見表2。

圖2 三軸轉臺實驗Fig.2 Three-axis turntable experiment

表2 慣性器件參數表Tab.2 Performance index of IMU

三軸轉臺驗證實驗時，由于無法同步錄取轉臺實時姿態，因此沒有給出初始對準姿態角誤差曲線。圖3為標準Kalman濾波與自適應濾波估計失準角曲線，粗對準結束后，航向角誤差為 13.98′。當采用標準Kalman精對準時，最終航向角誤差為0.73′；而采用自適應濾波器，最終航向角誤差為0.18′，姿態角對準精度得到了提高。同時可以看出，當轉位機構轉動時，Kalman濾波器估計角度會隨著轉位機構的轉動發生小角度擾動，而自適應濾波器的收斂顯得更加平穩，能夠更好地實時跟蹤轉位機構的動態變化，見表3。

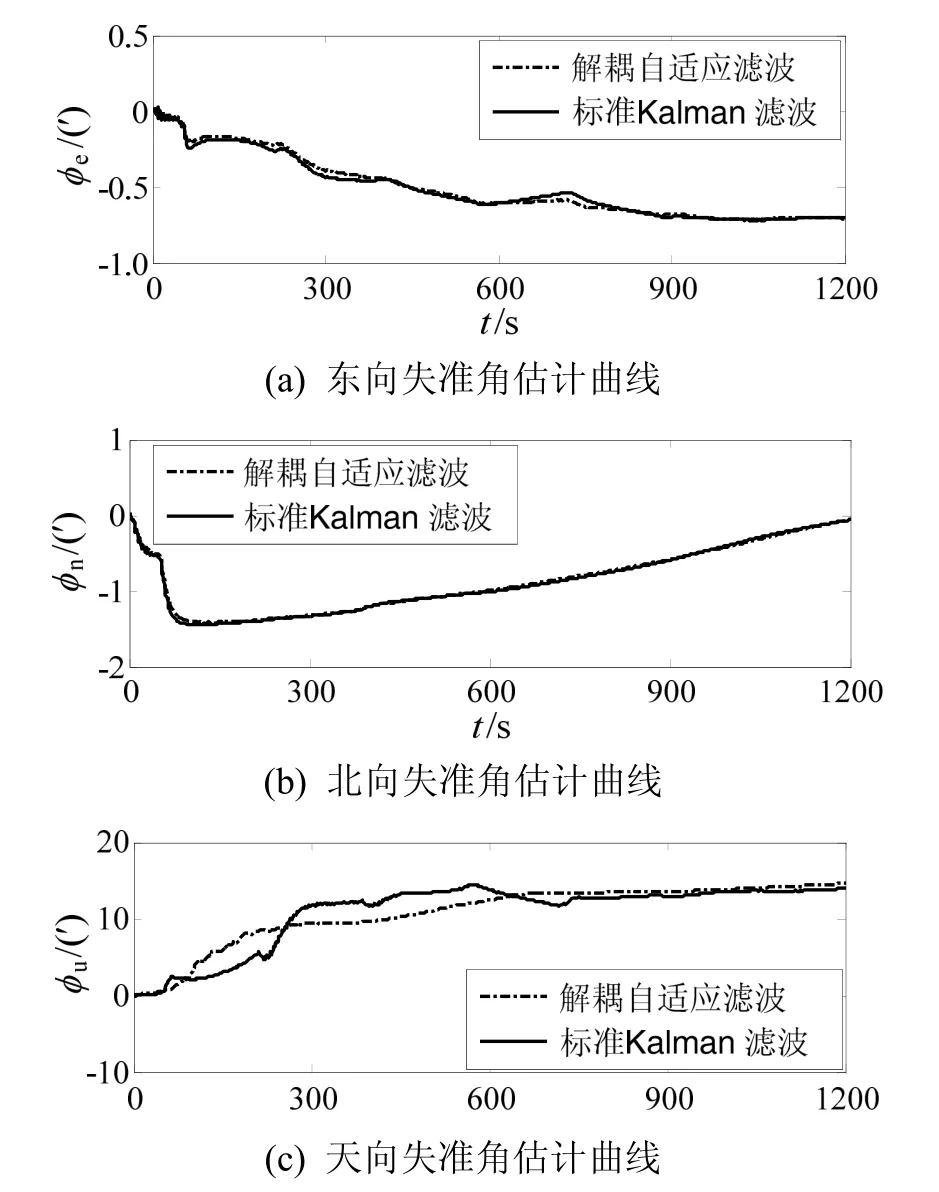
圖3 轉臺驗證失準角估計曲線Fig.3 Attitude error estimation of turntable experiment

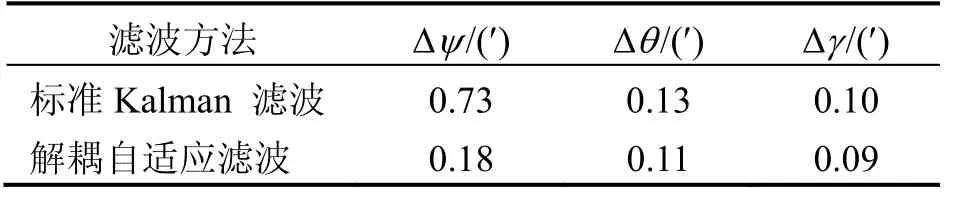
表3 轉臺驗證姿態角誤差表Tab.3 Attitude error of turntable experiment

為了進一步說明自適應濾波器對準精度優于標準Kalman濾波器，在此基礎上分別進行6 h純慣性導航，定位誤差如圖4所示。

由圖4可知，在Kalman濾波器精對準基礎上進行6 h純慣性導航，最終定位誤差為2.06 n mile，而當采用自適應濾波器進行精對準，6 h純慣性導航定位誤差為1.55 n mile，導航精度得到提高。

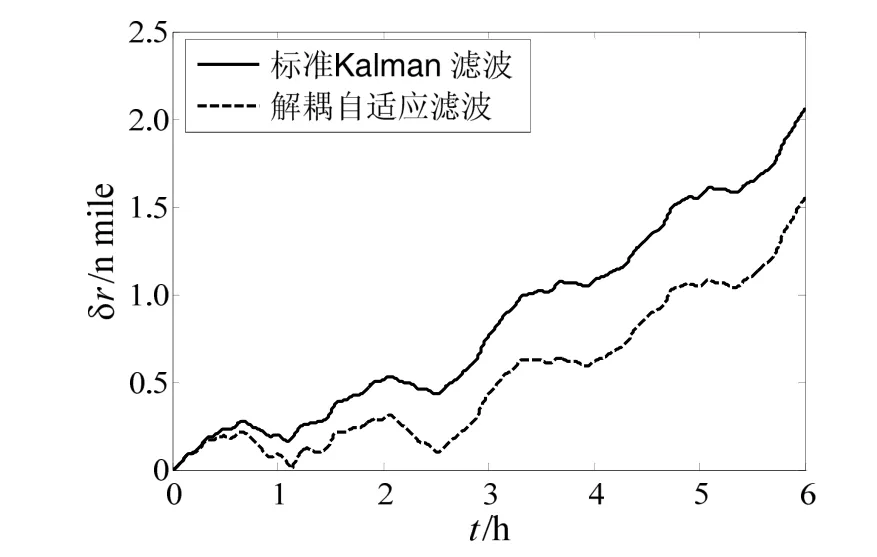
圖4 定位誤差對比曲線Fig.4 Curves of positioning errors

6 結 論

本文對旋轉 SINS初始對準方法進行了研究，給出了單軸旋轉 SINS誤差調制原理以及初始對準狀態方程和量測方程。提出了一種解耦自適應 Kalman濾波方法，該方法采用 Allan方差分析法估計量測噪聲的方差，系統噪聲方差與量測噪聲方差的估計過程互相獨立，從而避免了參數互相耦合引起的濾波精度下降等問題。進行了數學仿真和轉臺驗證實驗，結果表明本文所提出的方法對準精度要優于標準 Kalman濾波方法，且精對準過程中，采用自適應 Kalman濾波時系統具有更好的環境適應性。

（References）：

[1] Sun W, Xu A G, Che L N, et al. Accuracy improvement of SINS based on IMU rotational motion[J]. IEEE Aerospace & Electronic Systems Magazine, 2012, 27(8): 4-10.

[2] Zhang L D, Lian J X, Wu M P, et al. An improvement computation scheme of strapdown inertial navigation system using rotation technique[J]. Journal of Central South University, 2012, 19(5): 1258-1266.

[3] Lahham J I, Brazell J R. Acoustic noise reduction in the MK 49 ship’s inertial navigation system (SINS)[C]// Proceedings of the IEEE Position Location and Navigation Symposium. Monterey, USA, 1992: 32-39.

[4] Terry T, Emanuel L. The AN/WSN-7B marine gyrocompass/navigator[C]//Proceedings of the 2000 National Technical Meeting of the Institute of Navigation. Anaheim, USA, 2000: 348-357.

[5] Morrow R B J, Heckman D W. High precision IFOG insertion into the strategic submarine navigation system [C]//Proceedings of the IEEE Position Location and Navigation Symposium. Palm Springs, USA, 1998: 332-338.

[6] 黃鳳榮, 孫偉強, 翁海娜. 基于UKF的旋轉式SINS大方位失準角初始對準方法[J]. 中國慣性技術學報, 2010, 18(5): 513-517. Huang Feng-rong, Sun Wei-qiang, Weng Hai-na. Rotary SINS inertial alignment for large heading misalignment based on UKF[J]. Journal of Chinese Inertial Technology, 2010, 18(5): 513-517.

[7] Gao W, Zhang Y, Wang J G. Research on inertial alignment and self-calibration of rotary strapdown inertial navigation systems[J]. Sensors, 2015, 15: 3154-3171.

[8] 蘇宛新, 黃春梅, 劉培偉, 等. 自適應 Kalman濾波在SINS初始對準中的應用[J]. 中國慣性技術學報, 2010, 18(1): 44-47. Su Wan-xin, Huang Chun-mei, Liu Pei-wei, et al. Application of adaptive Kalman filter technique in initial alignment of inertial navigation system[J]. Journal of Chinese Inertial Technology, 2010, 18(1): 44-47.

[9] Wang Rong-ying, Liu Wen-chao, Bian Hong-wei, et al. Fast alignment algorithm with order-reduced filter for SINS[J]. Journal of Chinese Inertial Technology, 2016, 24(5): 607-611.

[10] Li K, Gao P Y, Wang L, et al. Analysis and improvement of attitude output accuracy in rotation inertial navigation system[J]. Mathematical Problems in Engineering, 2015(1): 1-10.

[11] 胡杰, 程向紅, 朱倚嫻, 等. 單軸旋轉捷聯慣導系統姿態和航向角在線組合校正[J]. 東南大學學報(自然科學版), 2016, 46(3): 494-498. Hu Jie, Cheng Xiang-hong, Zhu Yi-xian, et al. On-line integrated correction of attitude and heading for singleaxis rotary SINS[J]. Journal of Southeast University (Natural Science Edition), 2016, 46(3): 494-498.

[12] 李楊, 胡柏青, 覃方君, 等. 光纖陀螺信號的解耦自適應Kalman濾波降噪方法[J]. 中國慣性技術學報, 2014, 22(2): 260-264. Li Yang, Hu Bai-qing, Qin Fang-jun, et al. De-noising method of decoupling adaptive Kalman filter for FOG signal[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 260-264.

Refined alignment in rotary SINS based on Allan variance decoupling adaptive filter

HU Jie, CHENG Xiang-hong, ZHU Yi-xian
(Key Laboratory of Micro-Inertial Instrument and Advanced Navigation Technology, Ministry of Education, Southeast University, Nanjing 210096, China)

The refined alignment for rotary strapdown inertial navigation system (SINS) is studied. The adaptive Kalman filtering alignment is proposed to solve the problems of low filtering performance derived from uncertain noise caused by rotating disturbance of indexing mechanism and uncertain errors of inertial device in measurement equations. Sage-Husa is a generally used adaptive filtering algorithm, but it has the defection that the noise parameters are strongly coupled. Here, the relationship between the Allan variance and the measurement noise variance is studied by using the Allan variance filter which has the characteristics of band-pass filtering, and a filtering method is proposed, which can effectively overcome the strong coupling problem of traditional Sage-Husa filtering algorithm. The verifications by simulation and real inertial system are given, and the results show that the accuracy of the adaptive Kalman filtering algorithm is about 0.6′ higher than that of the conventional Kalman filtering algorithm, and the adaptive Kalman filtering algorithm is able to restrain the influence of the outside interference errors in the attitude error estimation process. Therefore, the adaptive Kalman filtering algorithm is a better refined alignment algorithm, which can be used to improve the accuracy of initial alignment of the rotary SINS.

rotary SINS; refined alignment; Allan variance; adaptive Kalman filtering

U666.1

A

1005-6734(2017)02-0156-05

10.13695/j.cnki.12-1222/o3.2017.02.004

2016-12-26；

2017-03-20

國家自然科學基金項目（61374215）

胡杰（1987—），男，博士研究生，從事慣性測量與組合導航研究。E-mail: hj_student@163.com

聯 系 人：程向紅（1963—），女，教授，博士生導師。E-mail: xhcheng@seu.edu.cn