高精度慣導系統重力擾動的阻尼抑制方法

翁海娜，李鵬飛，高 峰，胡小毛，張宇飛

（天津航海儀器研究所，天津300131）

高精度慣導系統重力擾動的阻尼抑制方法

翁海娜，李鵬飛，高 峰，胡小毛，張宇飛

（天津航海儀器研究所，天津300131）

重力擾動已經成為高精度長航時慣導系統的主要誤差源之一。針對船用高精度慣導系統的重力擾動抑制問題，從艦船INS誤差模型出發，推導了重力擾動在慣導系統中的傳播特性。仿真結果表明垂線偏差將引起系統較大的舒拉振蕩誤差。為抑制重力擾動對系統的影響，引入常速度誤差反饋阻尼網絡和相位超前串聯阻尼網絡。分析了重力擾動在水平阻尼網絡中的傳遞特性，實現了相應濾波器的設計。在此基礎上完成了實驗驗證，海上試驗結果表明，所引入的兩種阻尼網絡都能夠阻尼掉重力擾動引起的舒拉振蕩型導航誤差，其中，相位超前串聯阻尼網絡效果更優，抑制率達到70%以上。

重力擾動；垂線偏差；水平阻尼；高精度慣性導航系統

在導航解算過程中，加速度計無法區分運動加速度和重力加速度。一般采用正常重力模型來代替實際重力。由于實際地球的形狀不規則、內部質量不均勻、參考橢球和大地水準面不完全吻合等原因，重力矢量和正常重力模型的計算值有所偏差，這種偏差稱為重力擾動。重力擾動分為垂線偏差和重力異常兩部分。隨著慣性器件精度的不斷提高和高精度慣性導航系統需求的發展，擾動重力成為高精度慣導的一項主要誤差來源。

解決重力擾動問題一般采用利用外部信息對重力擾動進行補償的方法：文獻[3]采用了三種分辨率的重力網格數據對垂線偏差進行差值補償；文獻[4]利用GPS和慣導的速度誤差作為觀測對重力異常進行Kalman濾波，并采用濾波后得到的重力異常值對慣導的重力異常項補償。以上的方法均基于有合適的外部參考信息可用時才能得以實現。對于水下載體，在無精確外界信息對重力擾動進行補償的情況下，要想獲得高精度的導航結果，必須采取自主方法來抑制重力擾動對系統的影響。

本文基于重力擾動在慣導系統中的誤差傳播方程，提出利用水平阻尼網絡抑制重力擾動對系統影響的方法，從兩種典型低階網絡出發推導了重力擾動下系統誤差傳播規律，通過實際試驗數據分析兩種水平阻尼網絡對重力擾動的抑制效果。

1 重力擾動矢量對慣導系統的影響

1.1 重力擾動矢量

重力擾動矢量是大地水準面上某一點在參考橢球表面上對應位置的實際重力值g與橢球上正常重力值g0的差值δg，可表示為

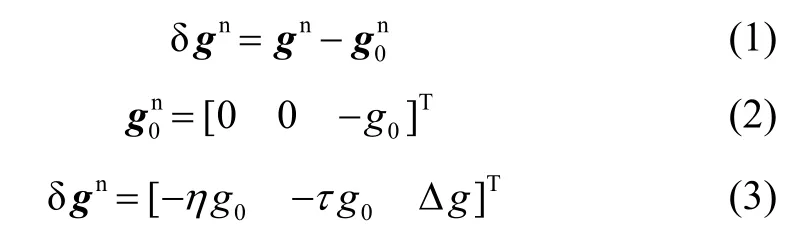
式中：g0為正常重力模型下的重力計算值；η為子午面垂線偏差，繞東向軸為正；τ為卯酉面垂線偏差，繞北向軸為正；Δg為重力異常值。

1.2 重力擾動矢量對導航誤差影響

在忽略陀螺儀和加速度計元件誤差的基礎上，通過對艦船INS誤差模型的分析，研究了各個方向重力擾動分量對導航誤差的影響：

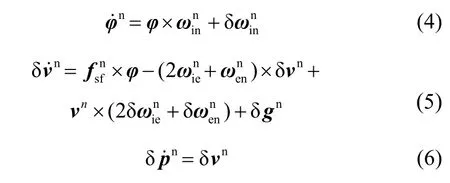
式中：φ為姿態角誤差；δv為速度誤差；δp為位置誤差。聯合式(4)～(6)可得慣性導航系統誤差方程為

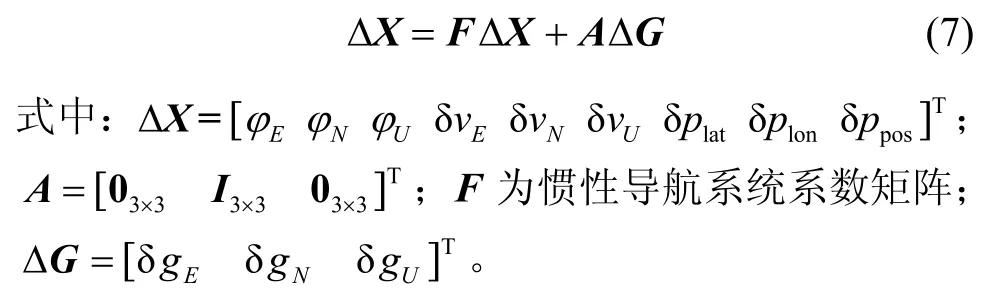
由式(7)可知，導航坐標系下各方向的重力擾動可等效成相同方向的加速度計零位，從而引起導航誤差。其中，垂線偏差直接將重力值分解到水平方向上，形成等效加速度計零位，而重力異常則與慣導系統的姿態誤差角相耦合后才等效成加速度計零位，其量值很小，幾乎可忽略不計。

圖1、圖2分別為當卯酉面垂線偏差ξ=20″時加入垂線偏差和不加入垂線偏差的速度、位置誤差對比曲線。圖3、圖4分別為當重力異常為95 mGal時加入重力異常和無重力異常時的速度、位置誤差對比曲線。

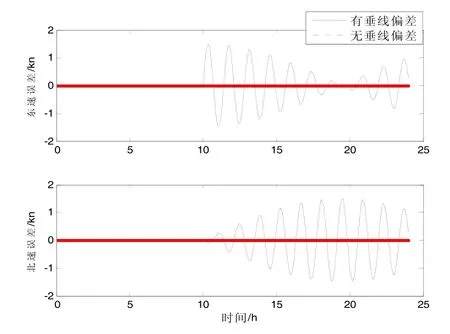
圖1 垂線偏差對速度誤差的影響曲線Fig.1 Influence of vertical deviation on speed error

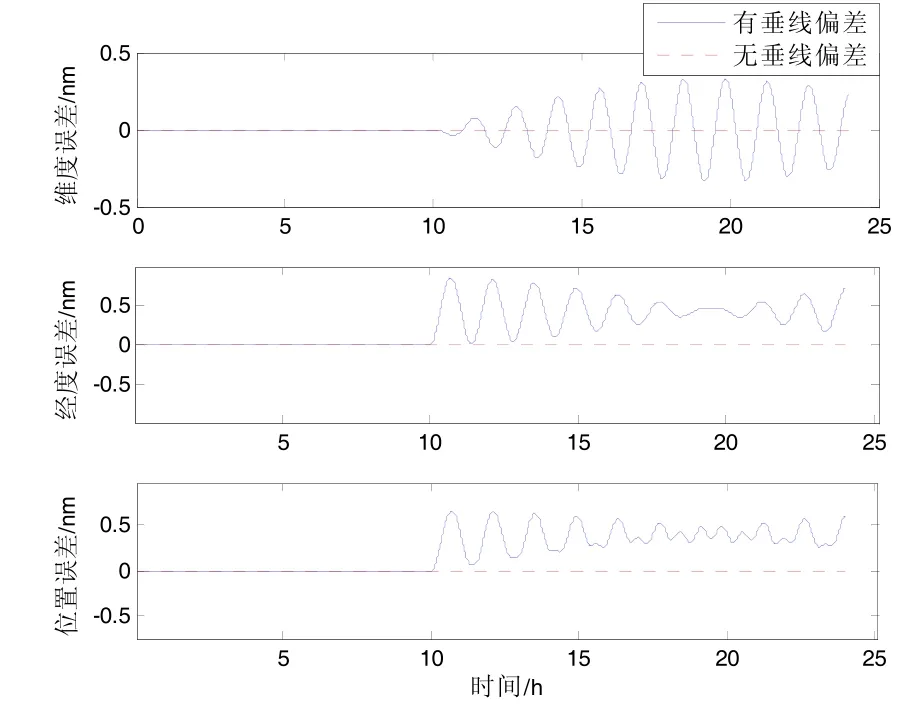
圖2 垂線偏差對定位誤差的影響曲線Fig.2 Influence of vertical deviation on position error

圖3 重力異常對速度誤差的影響曲線Fig.3 Influence of gravity anomaly on speed error

圖4 重力異常對系統定位誤差的影響曲線Fig.4 Influence of gravity anomaly on position error

仿真結果表明：1）20″的垂線偏差帶來的導航定位常值誤差約為0.4 nmile，而95 mGal的重力異常帶來的導航定位常值誤差為 0 nmile；2）慣性導航系統中由重力擾動引起的導航誤差具舒拉振蕩特性。

2 重力擾動的抑制方法

第1.2節的分析及仿真結果顯示，垂線偏差會引起較大的舒拉振蕩的誤差。由于垂線偏差所產生的系統誤差可以等效為加表零偏引起的系統誤差，因而可以采用水平阻尼網絡對重力擾動產生的系統誤差進行抑制。

2.1 水平阻尼網絡分析

基于單通道舒拉阻尼回路誤差傳遞函數框圖[6],建立舒拉阻尼回路的速度誤差δv和位置誤差δr方程為

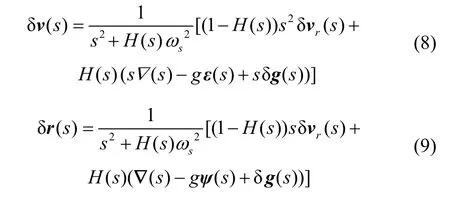
式中：?為加速度計測量誤差，ε為陀螺漂移角速度誤差，δvr為外部參考速度誤差，δg為垂線偏差，sω為舒拉角頻率，ψ為陀螺漂移角度增量誤差。

2.2 阻尼網絡選取

為了抑制重力擾動帶來的導航誤差，選擇常速度誤差反饋阻尼網絡和相位超前串聯校正網絡。常速度誤差反饋阻尼網絡和相位超前串聯校正網絡的傳遞函數分別為：

常速度誤差反饋網絡：

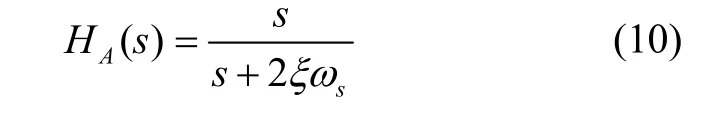
相位超前串聯校正網絡：

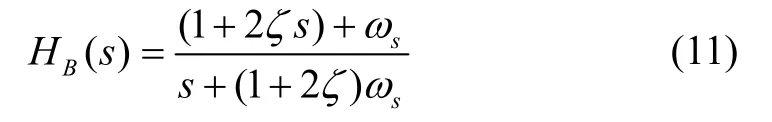
式(12)(13)分別為當舒拉回路阻尼網絡為常速度誤差反饋網絡時的速度誤差和位置誤差，式(14)(15)分別為當舒拉回路阻尼網絡為相位超前串聯網絡時的速度誤差和位置誤差。

表1為兩種校正網路的舒拉阻尼回路的穩態位置誤差，表2為兩種校正網絡的舒拉阻尼回路的位置誤差頻率特性。

表1 舒拉阻尼回路穩態位置誤差Tab.1 Steady-state position errors based on Schuler damping loop

表2 舒拉阻尼回路位置誤差頻率特性Tab.2 Frequency characteristics of position errors based on Schuler damping loop

由圖3得，北向水平阻尼回路的開環傳遞函數為

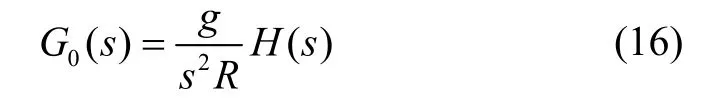
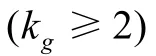
3 實際系統試驗驗證

為了驗證所設計的兩種水平阻尼網絡對重力擾動誤差的抑制效果，利用某激光捷聯慣性導航系統進行了實船海上試驗驗證。

首先編寫了嵌入式軟件，確保激光捷聯慣性導航系統中無阻尼通道和水平阻尼通道導航解算同時運行。水平阻尼通道解算采用超前串聯校正網絡，同時，可根據海況和運動狀態實現阻尼和無阻尼狀態的自動切換。之后，利用實測海上試驗的測量數據作為解算數據，離線進行了常速度誤差反饋阻尼網絡導航解算，以用來比較重力擾動誤差的抑制效果。

圖5為海上試驗所在海域重力異常區域跨度圖。

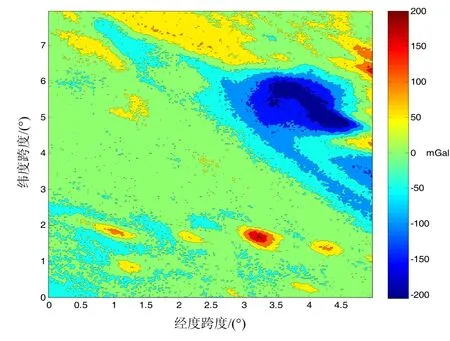
圖5 重力異常區域經緯度跨度圖Fig.5 Span of latitude and longitude in gravity anomaly area

下面分別為通過實驗得到的兩種阻尼網絡和無阻尼解算結果對比曲線。圖6、圖7分別為常速度誤差反饋網絡解算結果和無阻尼解算結果速度、位置誤差的歸一化處理后的對比圖。圖8、圖9分別是超前串聯校正網絡解算結果和無阻尼解算結果的速度、位置誤差歸一化處理后的對比圖。從圖中可以看到，當艦船經過重力擾動區域時，系統無阻尼解算速度和位置誤差有比較大的波動，由1.2節的推導及仿真，可以認為這是由此區域存在的垂線偏差引起的。

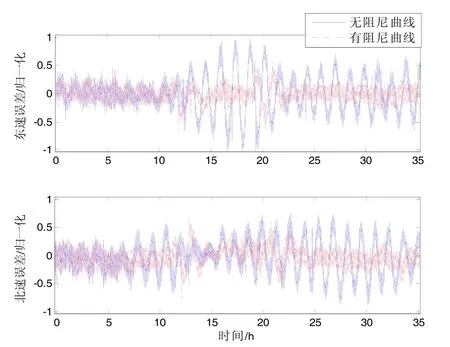
圖6 常速度誤差反饋校正網絡和無阻尼解算速度誤差對比Fig.6 Comparison on speed errors of constant velocity error feedback network and non-damping solution

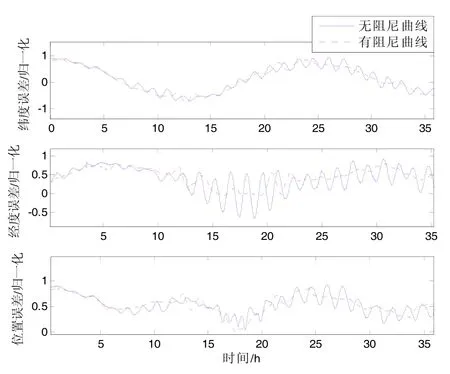
圖7 常速度誤差反饋校正網絡和無阻尼解算位置誤差對比Fig.7 Comparison on position errors of constant velocity error feedback network and non-damping solution

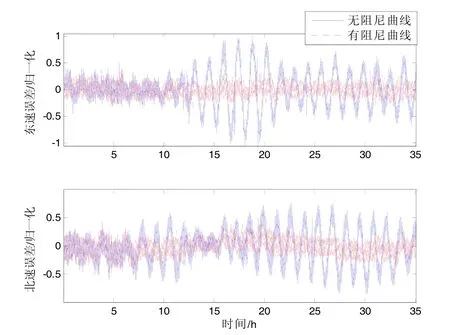
圖8 超前串聯校正網絡和無阻尼解算速度誤差對比Fig.8 Comparison on speed errors of lead-series correction network and non-damping solution

圖6～9的實驗結果表明，在重力擾動區域，超前串聯水平阻尼網絡和常速度誤差反饋水平阻尼網絡對重力擾動均有比較好的抑制效果，超前串聯水平阻尼網絡對于速度誤差和位置誤差的抑制效果更佳，速度誤差的抑制率可以達到70%以上。

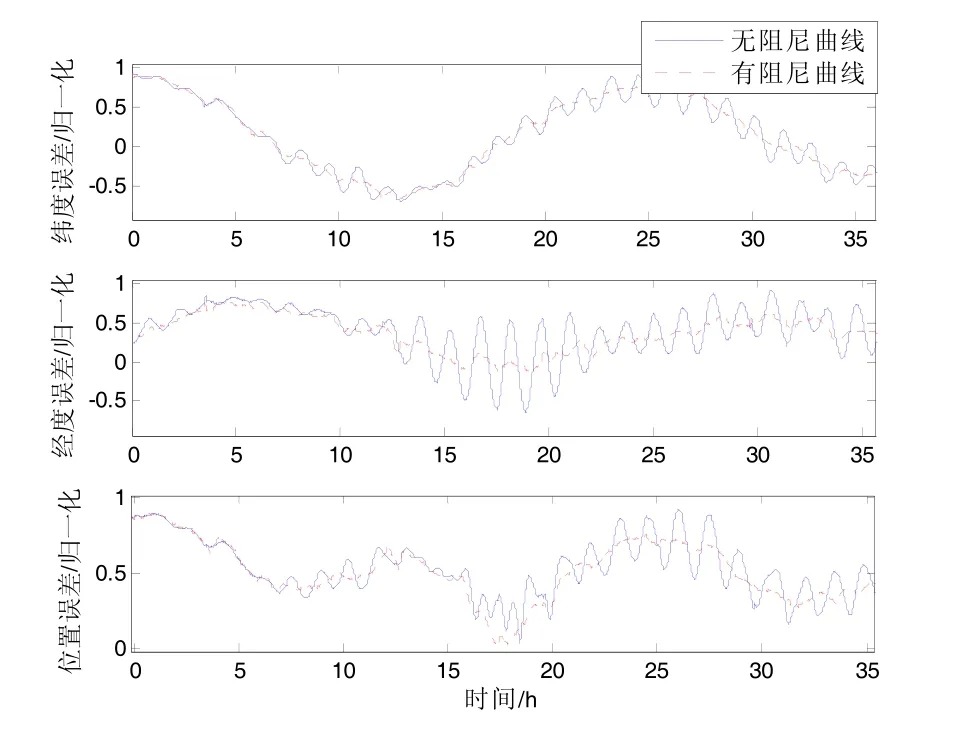
圖9 超前串聯校正網絡和無阻尼解算位置誤差對比Fig.9 Comparison on position errors of lead-series correction network and non-damping solution

4 結 論

重力擾動包括垂線偏差和重力異常。本文通過分析和仿真認為，垂線偏差將引起系統較大的舒拉振蕩誤差，而重力異常對于系統導航誤差的影響相比垂線偏差的影響可以忽略不計。在無外界精確的重力擾動補償信息的情況下，可以通過引入水平阻尼網絡來抑制重力擾動的影響。

本文分別對常速度誤差反饋網絡和相位超前串聯網絡進行了分析，并設計了相應阻尼濾波器。為說明兩種阻尼濾波方法對重力擾動影響的抑制效果，利用某激光陀螺捷聯慣導系統，開展了海上驗證試驗。

重力擾動區域的海上試驗結果表明，所設計的兩種水平阻尼網絡均能有效抑制重力擾動引起的系統誤差。其中，相位超前串聯阻尼網絡更優，其速度誤差的抑制率可以達到 70%以上，系統誤差量級基本和無重力擾動區相當。

（Reference）：

[1] Welker T C, Richard E H, Pachter M. Modeling Earth’s gravitation gradients for GPS-free navigation[C]//ACC. Washington DC, 2013: 1602 -1607.

[2] Li S, OuYang Y, Chang G, et al. Analysis on effecting mode of several essential factors to gravity aided navigation[J]. Journal of Chinese Inertial Technology, 2012, 20(4): 410-413.

[3] 趙忠, 王鵬. 高精度慣性導航系統垂線偏差影響與補償[J]. 中國慣性技術學報, 2013, 21(6): 701-705. Zhao Z, Wang P. The influence and compensation of vertical deviation of high inertial navigation system[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 701-705.

[4] 周瀟, 楊功流, 王晶, 等. 基于 Kalman濾波原理對慣導中重力擾動的估計及補償方法[J]. 中國慣性技術學報, 2015, 23(6): 721-726. Zhou Xiao, Yang Gong-liu, Wang Jing, et al. Estimation and compensation method of gravity disturbance in inertial navigation based on Kalman filtering principle[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 721-726.

[5] Yao Y, Shen X, Zhou Y, et al. Analysis of gravity disturbance influence on strapdown inertial navigation system [J]. Journal of Geodesy and Geodenamics, 2011, 31(6): 111-116.

[6] He Q, Gao Z, Wu Q, Fu W. Design of horizontal damping network for inertial navigation system based on complementary filter[J]. Journal of Chinese Inertial Technology, 2012, 20(2): 158-161.

[7] Deng T, Yang X. Error analysis of horizontal damping state outside platform inertial navigation system[J]. Electrooptical and control, 2011, 18(11): 96-100.

[8] Rummel R, Yi W, Stummer C. GOGE gravitational gradio- metry[J]. Journal of Geodesy, 2011, 85: 777-790.

[9] Man X, Fang J CH, Ning X L. An overview of autono= mous navigation for a gravity-assist interplanetary spacecraft[J]. Progress in Aerospace Sciences, 2013, 63: 56-66.

[10] Zhao W, Yang G, Zhuang L, et al. Study on level damp of double inertial navigation system[J]. Journal of System Simulation, 2007, 19(5): 1109-1111.

Damping suppression method for gravity disturbance of high-precision inertial navigation system

WENG Hai-na, LI Peng-fei, GAO Feng, HU Xiao-mao, ZHANG Yu-fei
(Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)

The gravity disturbance is one of the main error sources of marine high-precision inertial navigation system, which is consisted of two parts: vertical deviation and gravity anomalies. The propagation characteristics of gravity disturbance in the navigation system are deduced based on the SINS error model, and the simulation results show that the vertical deviation will cause much larger Schular oscillation error than the gravity anomalies which can be ignored. Since the system error caused by the vertical deviation can be equivalent to the one caused by the bias of the accelerometer, a constant velocity error feedback network and a phase advance series damping network are introduced to suppress the gravity disturbance’s influence by an autonomous method. The error transfer equation of gravity anomaly in horizontal damping circuit is deduced, and the corresponding filter design is achieved. Based on these, the sea experiments are carried out, which show that the introduced horizontal damping networks can significantly damp out the Schular oscillation errors caused by the gravity disturbance, in which the phase-advance series damping network has an even better inhibitory effect, whose inhibition rate is up to more than 70%.

gravity disturbance; vertical deviation; level damping; high precision inertial navigation system

U666.1

A

1005-6734(2017)02-0141-05

10.13695/j.cnki.12-1222/o3.2017.02.001

2017-01-24；

2017-03-26

國家安全重大基礎研究資助項目（613219）

翁海娜（1969—），女，研究員，碩士生導師，研究方向為導航、制導與控制。E-mail: wenghaina@126.com