含抗雷線圈的AT供電牽引網故障測距方法研究

葛海波，張家念，郭 華

?

含抗雷線圈的AT供電牽引網故障測距方法研究

葛海波，張家念，郭 華

基于對含抗雷線圈的全并聯AT供電回路研究，提出橫聯電流比原理故障測距的修正方法。

抗雷線圈；故障測距；橫聯電流比；全并聯AT供電

0 引言

目前我國高鐵（客運專線）供電系統主要采用全并聯AT供電方式，該運行方式常用的故障測距原理為吸上電流比和橫聯電流比原理。在雷擊密集的鐵路線路，為了保護牽引變電所內供電設備，牽引所亭饋線出口處均安裝了抗雷線圈。由于抗雷線圈的存在，導致采用橫聯電流比原理故障測距時產生較大誤差。筆者通過對含抗雷線圈的全并聯AT供電回路進行研究，提出橫聯電流比原理的修正方法。

1 含抗雷線圈牽引網等值電路

1.1 含抗雷線圈的牽引網

目前，我國所采用的全并聯AT供電方式，在AT所和分區所處將上下行接觸網（T）、正饋線（F）和鋼軌（R）并聯連接，該供電方式牽引網可簡化如圖1所示，其中變電所設置2臺牽引變壓器，1臺主用1臺備用，變壓器二次線圈中點抽出接地并接鋼軌，在變電所饋線不設自耦變壓器。CB1、CB2分別為下、上行雙極斷路器，AT1、AT2分別為AT所、分區所的自耦變壓器，T2、F2、R2為上行線路的接觸網、正饋線、鋼軌，T1、F1、R1為下行線路的接觸網、正饋線、鋼軌，KL為牽引所亭上網處串接的抗雷線圈。

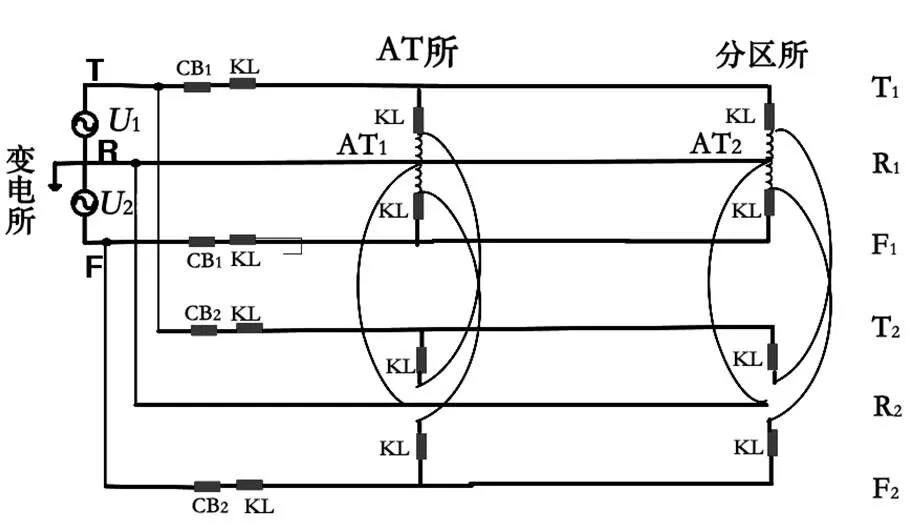
圖1 全并聯AT供電牽引網示意圖

圖2為我國高鐵（客運專線）接觸網橫截面圖，從圖中可以看出下行接觸線（T1）和上行接觸線（T2），下行正饋線（F1）和上行正饋線（F2）均為對稱布置。基于這種對稱的特點，可以采用下面提到的廣義對稱分量法分析全并聯AT供電牽引網。

圖2 全并聯AT供電接觸網橫截面圖

1.2 含抗雷線圈的牽引網等值電路

文獻[1]給出了廣義兩相對稱分量法基本概念及簡單應用，此處簡述如下。

當空間存在相對稱子系統，且整個閉合空間有個對稱布置的這種子系統時，×個物理量和×個對稱分量有如下關系：

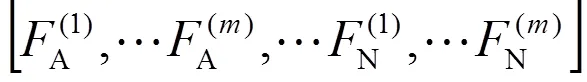
[00 01…(1-n)(1-m)] =（2）

復線全并聯AT供電牽引網存在4個基本回路：T1對地、T2對地、F1對地、F2對地，通過對4個回路的阻抗進行分析，可將牽引網T1、F1、T2、F2看作是A、B、C、D四相電路。根據牽引網特性，做以下假設：（1）上下行線路參數相同；（2）AT為理想變壓器；（3）接觸網和正饋線自阻抗的均值作為其運算過程中的自阻抗。

上下行線的接觸網和正饋線單位公里自阻抗的平均值作為每相單位公里的自阻抗：

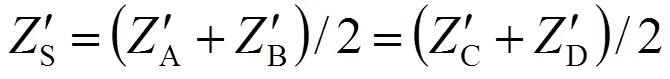
上行接觸網和上行正饋線、下行接觸網和下行正饋線單位公里的互阻抗為

（4）

上行接觸網和下行接觸網、上行正饋線和下行正饋線單位公里的互阻抗為

上行接觸網和下行正饋線、上行接觸網和下行正饋線單位公里的互阻抗為

（6）

由式（1）—式（6）得出全并聯AT供電牽引網單位序阻抗為

當== 2時，式（1）、式（2）中的坐標變換矩陣[]n(m)及其逆矩陣如下：

，（8）

對全并聯AT牽引網的電壓、電流進行坐標變換，滿足如下計算式：

（10）

由式（10）可以得出序電流流向，如圖3所示。

圖3 序電流流向示意圖

文獻[1，2]均對電源、自耦變壓器、橫聯線在各序電流流通時的特性進行了研究，本文直接引用文獻[2]中的推導結果，并在推導結果中考慮增加抗雷線圈。含抗雷線圈的全并聯AT供電牽引網正常序網如圖4所示。

圖4 含抗雷線圈的全并聯AT供電牽引網正常序網圖

2 含抗雷線圈牽引網橫聯電流比修正

對高鐵（客運專線）常見的T線對地故障和T線對F線故障的修正測距公式進行推導，F線對地故障的修正和T線對地故障類似。

2.1 T線對地短路（T-R）分析

假設故障發生在AT0—AT1區段內，發生下行T線（T1）對地短路。短路電流等于T1（A）相流入大地電流，其他相直接流入大地電流為0，且T1（A）相短路點為0。所以故障電路邊界條件為

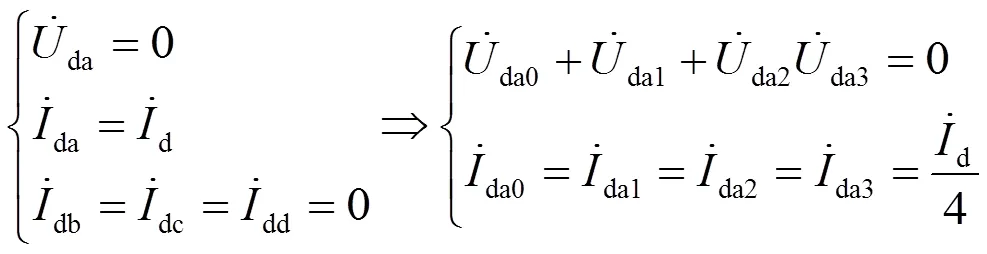
按圖4可以畫出下行T1（A）相故障復合序網圖，如圖5所示。由圖5可以看出，橫聯電流只在2序、3序網中流通。

圖5 全并聯AT供電T故障復合序網圖

圖5中為AT0到故障點的距離，1為AT0—AT1的距離，2為AT1—AT2的距離。

AT0處橫聯電流為

AT1處橫聯電流為

（13）

式中，為AT與橫聯線對2序電流的分流系數。

假設：

將式（14）代入式（12）、式（13）中，得

（15）

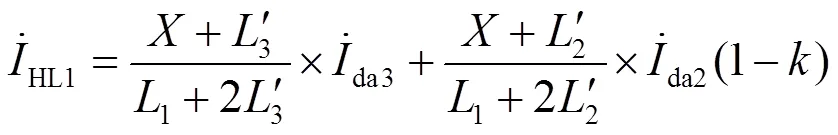
文獻[3]對復線AT牽引網序阻抗算法進行了推導，并根據實際牽引網的參數計算0序—3序阻抗，其大小分別為0.315 8+j1.781 3，0.110 6+j0.335 7，0.128 0+j0.373 8，0.113 4+j0.315 3。

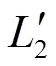
將式（11）、式（17）代入式（15）、式（16）化簡可得

（18）

式（19）即為含抗雷線圈牽引網的橫聯比測距公式，當牽引網中沒有抗雷線圈時，即，則式（19）可簡化為

（20）

式（20）為不含抗雷線圈的全并聯AT供電方式下的橫聯電流比計算公式。

由式（19）可得，含抗雷線圈牽引網的橫聯電流比測距公式為

=×(1+)-（21）

2.2 T線對F線短路（T-F）分析

假設故障發生在AT0—AT1區段內，發生下行T線（T1）對下行F線（F1）短路，即線路A、B發生短路。故障電路邊界條件為

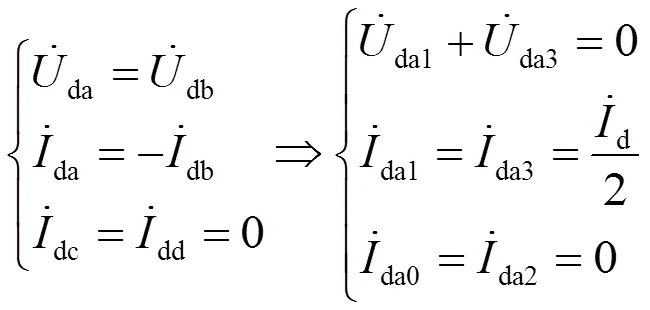
按圖4可以畫出下行T1—F1故障復合序網圖，如圖6所示，橫聯電流只在3序網中流通。

圖6 全并聯AT供電T-F故障復合序網圖

AT0處橫聯電流為

AT1處橫聯電流為

（24）

假設：

將式（25）代入式（23）、式（24），簡化得

（26）

比較式（21）和式（27）可以得出，T-R、T-F故障時含抗雷線圈牽引網的橫聯電流比測距公式相同。本文限于篇幅未推導F-R故障時橫聯電流比測距修正公式，F-R故障時橫聯電流比測距修正公式與式（21）、式（27）相同。

3 修正公式驗證

結合上文推導得出各種故障類型下含抗雷線圈牽引網的橫聯電流比測距公式，下面利用貴廣客專潮田變電所廣州方向供電臂短路實驗數據校驗測距修正公式的實用性。

3.1 T-R故障

故障點在AT所—分區所下行區段，故障點距離AT所13.781 km，AT所—分區所區間長度為14.02 km。圖7為短路時刻供電臂電流潮流圖。

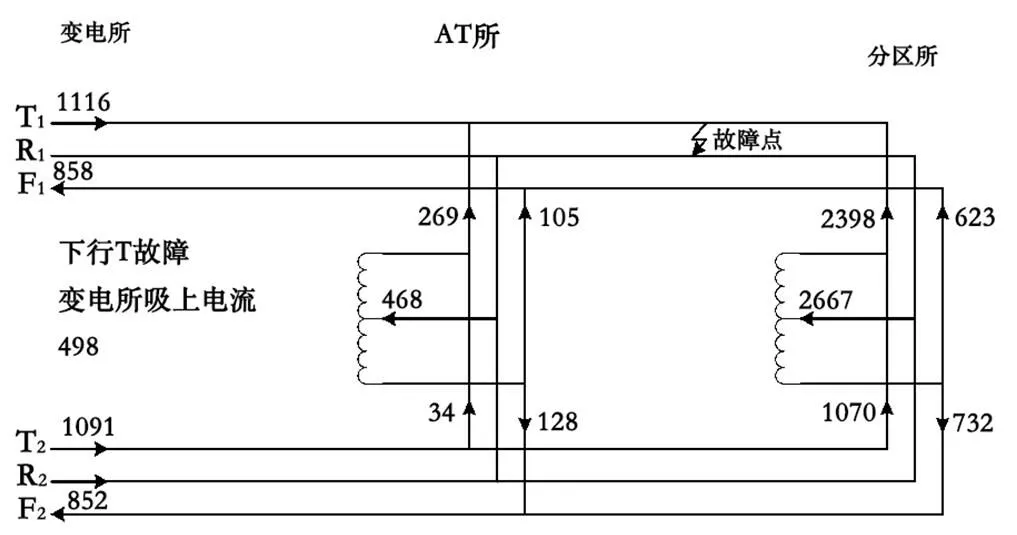
圖7 第二AT段T-R故障電流潮流圖

采用不修正測距式（20）計算，得

= 12.834 km，誤差0.947 km。

采用修正測距式（21）計算，得

= 13.970 km，誤差-0.189 km。

3.2 F-R故障

故障點在變電所—AT所上行區段，故障點距離變電所16.747 km，變電所—AT所區間長度為16.770 km。圖8為短路時刻供電臂電流潮流圖。

圖8 第一AT段F-R故障電流潮流圖

采用不修正測距式（20）計算，得

= 16.043 km，誤差0.704 km。

采用修正測距式（21）計算，得

= 16.866 km，誤差-0.119 km。

3.3 T-F故障

故障點在AT所—分區所下行區段，故障點距離AT所8.268 km，AT所—分區所區間長度為9.164 km。圖9為短路時刻供電臂電流潮流圖。

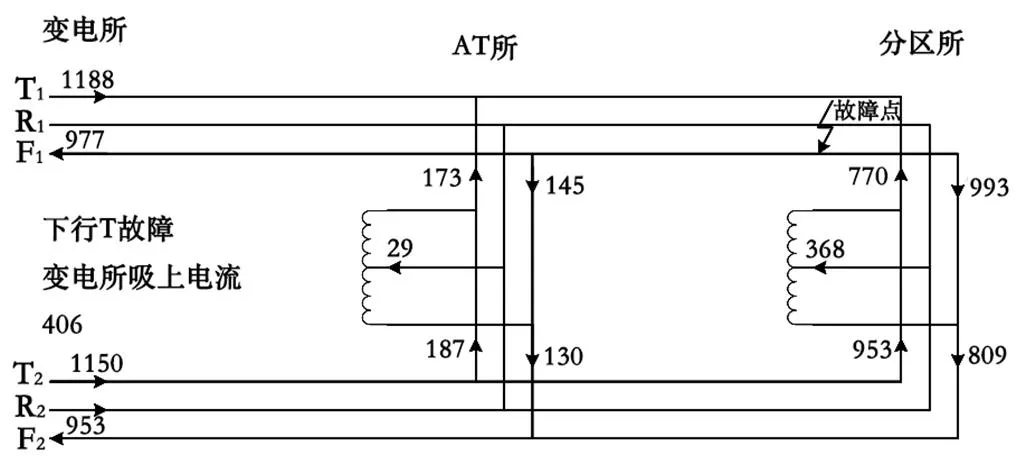
圖9 第二AT段T-F故障電流潮流圖

采用不修正測距式（20）計算，得

= 7.760 km，誤差0.508 km。

采用修正測距式（27）計算，得

= 8.515 km，誤差0.247 km。

4 結語

利用廣義對稱分量法對含抗雷線圈的全并聯AT供電牽引網進行了分析，推導出在T-R、F-R、T-F三種故障類型時橫聯電流比測距公式，結果均相同。最后采用現場實際短路數據對修正測距公式進行了驗證，結果表明采用修正測距公式計算故障距離誤差明顯變小。在利用修正測距公式時，等效長度和故障類型有關。

[1] 王鳳華. 廣義對稱分量法及其應用[[J]. 西南交通大學學報，1981，16（1）：1-12.

[2] 林國松. 牽引供電系統新型保護與測距原理研究[D]. 成都：西南交通大學博士學位論文，2010.

[3] 馬慶安. 高速鐵路供電若干問題的研究[D]. 成都：西南交通大學博士學位論文，2013.

[4] 李群湛，賀建閩. 牽引供電系統分析[M]. 西南交通大學出版社，2007.

[5] 曹建猷. 電氣化鐵道供電系統[M]. 北京：中國鐵道出版社，1993.

On the basis of researches of full parallel AT power supply circuit equipped with lightning arrestor, the paper puts forward the current ratio of cross coupling based modification method for fault location.

Lightning protection reactor; fault location; current ratio of cross coupling; full parallel AT power supply system

U223.8+3

B

1007-936X(2017)02-0009-05

葛海波.成都交大許繼電氣有限責任公司，工程師，電話：13540609002；張家念.南寧鐵路局南寧供電段，工程師；郭 華.成都交大許繼電氣有限責任公司，工程師。

2016-05-13