在教學中挖掘和滲透分類思想

陳愛珍

分類可以更好地揭示事物的本質，并將事物整理成具有不同等級的多層次系統，促進學生數學認知結構的發展。在教學中，教師應結合教材，聯系學生的實際，注重對數學分類思想的挖掘和滲透。

一、建立概念時，進行分類比較

在新知的教學過程中，對于一些典型的學習材料，教師要帶領學生對這些材料進行適當地分類，這樣有利于學生弄清概念之間的聯系與區別，建立清晰的概念。例如，建立“質數和合數”概念時，學生先分別找出下列這些數的因數：

1的因數有1 2的因數有1、2

3的因數有1、3 4的因數有1、2、4

5的因數有1、5 6的因數有1、2、3、6

19的因數有：1、19

28的因數有1、2、4、7、14、28

學生觀察比較后進行分類，可分為：（1）只有一個因數的；（2）只有2個因數的；（3）有2個以上因數的。然后教師帶領學生分類重點考察，抽象概括出：（1）一個數只有1和它本身兩個因數叫質數；（2）一個數除了1和它本身外還有別的因數叫合數；（3）1既不是質數也不是合數。

二、概念混淆時，進行分類區別

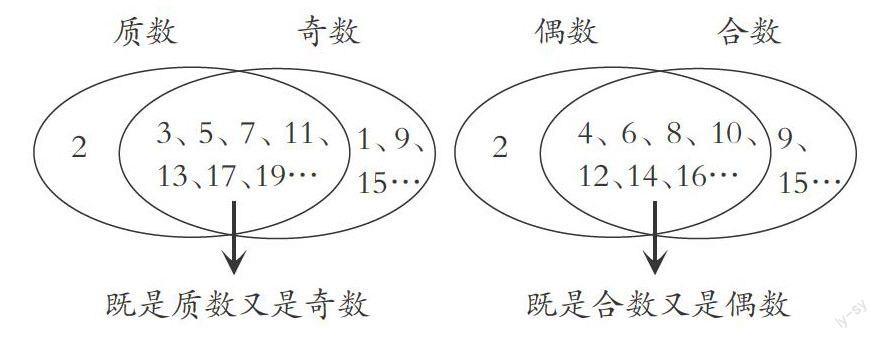
在教學中，我們可以積極引導學生對這些易混淆的概念進行分類區別，弄清它們之間的異同，幫助學生形成良好的知識結構。例如，“質數與奇數”、“合數與偶數”這兩組形貌相似的概念，學生往往會混淆，因此可設計下圖幫助學生進行分類區別：

三、復習小結時，進行分類梳理

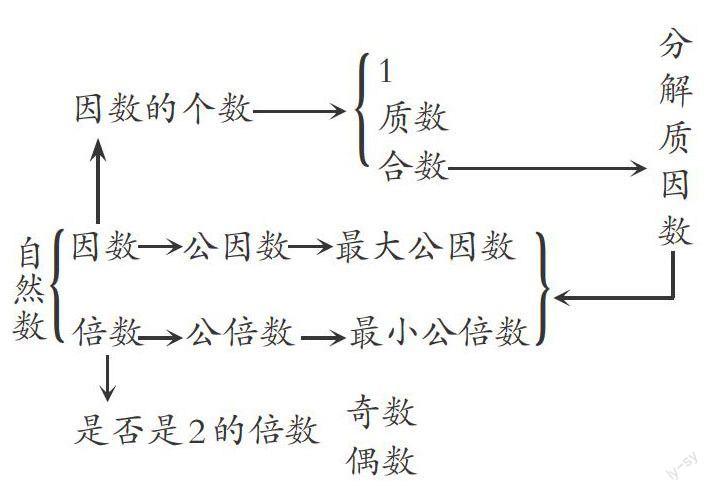
在復習階段，通過分類可以使數學知識條理化、系統化、結構化，有助于學生更好地掌握知識和形成良好的認知結構。例如，在概念相對集中的《因數和倍數》這一單元，復習時為了使學生對所學知識的回顧條理化、系統化，可設計下面的“分類梳理圖”作為復習的思路。

四、解疑排難時，進行分類討論

利用分類思想解題是小學數學中一個重要且有效的解題方法。尤其是對一些疑難題、靈活題的剖析，我們可以進行分類討論，做到既不重復又不遺漏，那么問題將被理解得更全面、更透徹。這樣有利于提高學生解題的條理性和正確率，培養學生思維的嚴密性，提高綜合分析的能力。例如，兩根同樣長的繩子，第一根截去[15]米，第二根截去它的[15]，剩下的繩子哪根長？這道題中繩子長多少沒有告訴我們，可以設繩子長為a米，a的取值有三種情況：a=1， a>1， a<1。

五、解決問題后，進行方法分類

在教學中，教師引導學生解決一些實際問題后，出現了多種解決問題的方法，這時教師有必要帶領學生對這些方法進行分類，從而使解決問題條理化，提高學生靈活解決數學問題的能力。例如，《組合圖形》的教學設計了如下的練習：這是學校教學樓占地的面積，你能用哪幾種方法解決這個問題？（出示下圖）

學生討論交流后，匯報如下幾種方法：

教師及時引導學生對上述幾種方法進行分類如下：

1.前3個圖形的解決方法我們把它稱為“分割法”，就是把一個組合圖形根據它的特征和已知條件，分割成幾個簡單的規則圖形，分別算出各個圖形的面積，最后求出它們面積的和。

2.第4個圖形的解決方法我們把它稱為“添補法”，就是將原圖形補充為基本圖形，然后求出整個圖形的面積，最后再減去補充部分的面積。

3.第5個圖形的解決方法我們把它稱為“移補法”，就是把圖形的某一部分割下來，再通過平移補到另一部分上，使它變成一個我們已學過的幾何圖形，然后再進行計算。

六、綜合練習后，進行策略分類

學生學過很多解決問題的策略，在所有的策略學習完以后，教師有必要引導學生將所學過的策略進行分類，讓學生靈活運用前面學過的策略解決稍復雜的問題，進一步體會策略在解決新穎的、稍復雜的問題過程中的作用，體會解決同一個問題的方法的多樣、策略的靈活。例如，《解決問題的策略》教學中設計如下的練習：

1. 小強、小華和小麗是好朋友。如果他們每兩人之間通一次電話，一共要通多少次電話？如果他們互相寄一張節日賀卡，一共要寄多少張賀卡？

2. 計算 [12]+[14]+[18]+[116]+[132]+[164]+[1128]+ [1256]

3. 1張桌子和4把椅子的總價是2700元，椅子的單價是桌子的[15]。桌子和椅子的單價各是多少元？

4. 兩筐蘋果共重56千克。從第一筐取出[29]放入第二筐，兩筐蘋果就同樣重。原來兩筐蘋果各重多少千克？（先把線段圖補充完整，再解答）

第一筐

第二筐

學生解答以上題目以后，教師及時引導學生，對所運用的解決問題的策略進行分類：

總之，數學分類思想是一種獲取知識的思維手段，亦是數學教學中一項不可忽視的內容。同時，分類思想方法的訓練是一個潛移默化的過程，它需要在教師精心的教學中滲透，在學生反復的實踐運用中逐步形成。