高中生數學思維的培養
聶靖翔+康淑瑰+田果萍
摘要:數學思維是數學地思考問題和解決問題的思維活動形式。要從問題出發,進行問題的設計、解題時的思維引導、解題后的反思與總結等一系列過程來培養高中生的數學思維。
關鍵詞:數學;思維;高中生;問題
中圖分類號:G632.0 文獻標志碼:A 文章編號:1674-9324(2017)20-0224-02
一、核心概念闡述
現代認知心理學認為思維是人的信息加工過程。信息加工的基本過程包括問題解決、模式識別和學習(即信息的獲取和存儲)[1]。數學思維是人腦和數學對象(空間形式、數學關系、結構關系)交互作用并按一般思維規律認識數學內容的內在理性活動,具有概括性、問題性和相似性等特征。[2]
二、數學思維的培養策略
教育的對象是學生,教師既要關注高中生的心理發展特點,又要適應高中生思維發展特征,還得兼顧數學思維的規律去設計高中生數學思維的培養策略。
學習方式是指每個人在學習時所具有的或偏愛的方式。[3]田果萍老師曾對高中生的數學學習方式做過調查研究,研究表明:68.0%的學生注重聽課;73.3%的學生大量做題;57.9%的學生進行總結。[4]這反映出聽課與練習成為高中生學習數學的雙主渠道,而且練習與聽課相比較而言顯得更加重要,高中生在構建自己的認知結構時十分重視知識的系統化,自主學習的意識與技能必有待提高。如果把數學問題比作修一條路的話,已知條件是材料,問題是設計圖,數學思維能力是建造過程,基礎能力就是地基。不管我們是領悟到還是學習到新的知識,都要有舊知識作為鋪墊,才能使全體學生進步,來培養數學思維能力。中國學生發展的核心素養,是以科學性、時代性和民族性為基本原則,以培養“全面發展的人”為核心,分為文化基礎、自主發展、社會參與三個方面。綜合表現為人文底蘊、科學精神、學會學習、健康生活、責任擔當、實踐創新六大素養,具體細化為國家認同等十八個基本要點。[5]
不同階段的學生因年齡特點在各學段的具體表現不同。“大眾數學”作為新課標基本理念的第一條,其理想結果是給所有學生“一雙能用數學視角觀察世間的眼睛,一個能用數學思維思考世間的頭腦”。[6]本文結合自己的學習經歷、實習經驗、大學期間在培訓機構擔任高中教師的經歷,從問題出發,進行設計、思維引導、解題后的反思與總結等一系列過程來培養學生的數學思維。
三、案例及其討論
案例1:從問題出發并進行問題的設計。
在課堂教學中教師應重視問題情境,盡可能的把數學問題與實際生活中的問題相關聯,與學生水平較為符合,來激發學生的興趣,從而調動學生的思維,培養學生的思維能力。例如:(1)賣一送一(即買一只茶壺送一只茶杯);(2)打9折(即按購買總價的90%付款)。其中還有一個前提條件是:購買茶壺3個以上(茶壺20元/個,茶杯5元/個)。[7]由此,不禁想到:這兩種優惠辦法有區別嗎?到底哪種更便宜呢?這種與生活息息相關的數學問題,更加容易吸引到學生的注意力,激發學生的興趣,更深入的思考從而鍛煉學生的數學思維。
案例2:解題時的思維引導。
首先:根據題意可以采用方程的思想去思考如下:
設茶壺X個,茶杯Y個,一共用去Z元。
第一種優惠方式:當Y
20X=Z(Y
當Y≥X,X>3,Y≥0時
20X+5(Y-X)=Z(Y≥X,X>3,Y≥0)
15X+5Y=Z(Y≥X,X>3,Y≥0)
第二種優惠方式:(20X+5Y)×0.9=Z(X>3,Y≥0)
18X+4.5Y=Z(X>3,Y≥0)
其次:從問題出發進行求解。題目問兩種優惠方式哪一個更便宜,商家既然給了多種優惠方式,就說明在合理的情況下使用合理的優惠方式最省錢,那么就要找在什么時候兩種方式花得錢一樣多,即Z相等。
當Y
20X=18X+4.5Y(Y
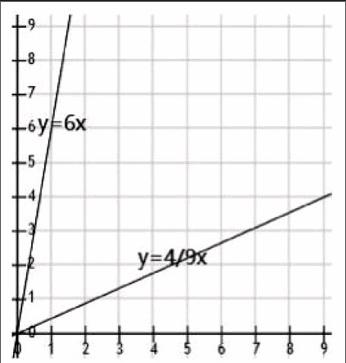
2X=4.5Y 即Y=4/9X
當Y≥X,X>3,Y≥0時
15X+5Y=18X+4.5Y(Y≥X,X>3,Y≥0)
0.5Y=3X,即Y=6X
解得當【0≤Y≤4/9X、Y≥6X、X>3】時,第二種優惠方式比較劃算;當【4/9X≤Y≤6X】時,第一種優惠方式比較劃算。
案例3:解決問題后的反思與總結。
題不在多,反思就好。從元認知理論的角度來看,反思與總結是數學思維培養的關鍵所在。問題解決之后,要反思解題的過程。學習反而是一個深化(包含優化)知識[8]與方法、監控思維的起航。學生深刻地體會到定義域是函數整體中不可分割的一部分(彌補了初次學習時的不全面性與不深刻性),加深了對分段函數的理解,領教了分類討論的必要性;在對解題步驟的審核驗證過程中,鍛煉了思維的縝密性;及時發現錯誤并及時糾正。這就是元認知體驗,使得思路暢通,解題速度加快,思維更加開闊,提高了數學和核心素養。
問題解決之后,還要反思題目特征。提高解決問題的能力,思維品質不僅是一種思維特征,而且也是一種認知方式,解題之后要舉一反三。數學思維的價值在于培養良好的思維品質:觸類旁通可以培養思維的廣闊性;想一想如果題目中的某個條件改變一下,會是什么結論,這種嘗試可培養思維的靈活性;揣摩解題規律可培養思維的深刻性;對解題速度進行評價可培養思維的批判性;能提出自己的觀點或方法可培養思維的獨立性。數學思維源于問題、成于問題,因此我們要抓住解題教學這一數學教育教學上的永恒主題,培養數學思維。
參考文獻:
[1][美]司馬賀.人類的認知[M].荊其誠,等,譯.北京:科學出版社,1986.
[2]任樟輝.數學思維論[M].桂林:廣西教育出版,1996.
[3]陳奇,劉儒.當代教育心理學[M].北京師范大學出版社,2006.
[4]田果萍,張生平,趙霞.高中生數學學習方式的調查與分析[J].教學與管理,2010,(9):52-53.
[5]中國學生發展的核心素養[EB/OL].[2016-12-10].http://edu.sina.com.cn/zl/edu/2016-09-18/11143922.shtml.
[6]劉兼,孫曉天.全日制義務教育數學課程標準解讀[M].北京師范大學出版,2003.
[7]吳水龍.高中數學教學中培養學生數學思維能力的嘗試[J].學周刊(B版),2014,(7)期:180-181.
[8]秦芳.高中學生數學思維能力的培養[J].渭南師范學院學報,2005,(20)(s2):117-118.

