基于分數階巴特沃斯濾波器的新型超級電容器

王 炎，崔建濤，劉 忠

?

基于分數階巴特沃斯濾波器的新型超級電容器

王 炎，崔建濤，劉 忠

（遼寧工程技術大學，電氣與控制工程學院，遼寧興城 125100）

超級電容器作為一種新型儲能元件在各個領域具有廣闊的應用前景。由于超級電容固有特性不是整數階的，因此建立一個精確且適用范圍更廣的模型具有重要的研究意義。介紹了超級電容器的基本模型，利用分數階巴特沃斯低通濾波器的優點，建立了一種新型超級電容器模型并驗證了模型的準確性，這可以擴大超級電容器的適用范圍，提高穩定性。

超級電容器；建模；分數階；巴特沃斯濾波器；等效電路模型；穩定性

超級電容器具有充電放電效率較高、適用溫度范圍較寬、循環壽命較長等特點，在儲存能量、電動汽車[1]等許多領域具有廣闊的應用前景。利用其對燃料電池的輔助作用的特點，可以在混合動力中起到很重要作用，并且有助于能量的再恢復[2]。建立精確的模型對進一步研究超級電容器特性、拓寬其適用范圍、完善元件材料的理論體系以及后續實際應用都具有重要意義。

2000年，Spyker等[3]提出了一個經典的等效電路模型，但此模型只反映了很小時間常數下的響應，只適用于簡單特殊情況。Gualous等[4]提出了使用電化學阻抗譜法構建一個超級電容器的二階等效電路，并且建立了電容值關于溫度的方程。2009年，Brouji等[5]用阻抗譜法研究了超級電容器生命周期。這些研究者們建立了等效電路模型并且提出了參數值是變化的觀點。通過研究已經提出的模型可知，模型的準確性和適用性一直是需要進一步完善的問題。

近年來，隨著分數階微積分的發展，其研究取得了很大進步，拓展了分數階的適用范圍，出現了包括分數階振蕩器、分數階巴特沃斯（Butterworth）濾波器、分數階PID控制器等新型電路。分數階微積分具有較長的記憶特性，使其成為可以更簡潔準確地描述材料、過程及系統復雜特性的重要途徑。巴特沃斯低通濾波器具有顯著的特點，即頻率響應曲線在通帶內，在最大限度上是平坦的，沒有太多起伏，而在阻頻帶則緩慢下降為零，且具有良好的線性相位特性、結構簡單、易于設計等優點[6]。低階巴特沃斯低通濾波器響應速度較快、超調量較小、穩定性較好；高階巴特沃斯低通濾波器檢波精度好[7]。

超級電容的固有多孔結構特性，電解質離子在極微觀的程度下形成雙電層儲能結構，其動態特性很難描述。Jonscher[8]的研究表明，構成電容的電解質材料體現出的是分數階特性，使得整數階電容的容抗形式不符合因果關系。建立超級電容器的整數階模型來描述它的特性可能會得出錯誤的結論，因此需要建立超級電容器的分數階模型。此外，現有分數階超級電容器建模的相關研究很少，超級電容器的分數階模型的研究顯得十分必要。本文提出了一種基于等分數階低通濾波器的超級電容器，利用分數階巴特沃斯低通濾波器的特點，同時結合基本超級電容器模型，可以擴大超級電容器的適用范圍并提高其穩定性、抗噪性等特點。

1 超級電容器的基本原理

1.1 雙電層原理

超級電容器（Supercapacitor）又稱為雙電層電容器[9]，這個名字是依據超級電容器充電放電的儲能原理所得。超級電容器在導體及電解液的分界面處會形成符號相反的穩定的雙層電荷，即雙電層(Helmholtz)，并在該層中儲能。雙電層超級電容器基于靜電電荷存儲原理，化學反應沒有發生在儲能過程中，具有非常高的充放電效率[10]。圖1所示為超級電容器物理結構，電荷儲存于電極多孔結構里；與傳統電容相比，超級電容器的靜電容量可達數萬法拉，這是因為其雙電層厚度較薄，并且多孔電極的表面積很高。影響超級電容器性能的因素有：電極材料的電導率、電極表面積、電化學性質及粒徑分布等。

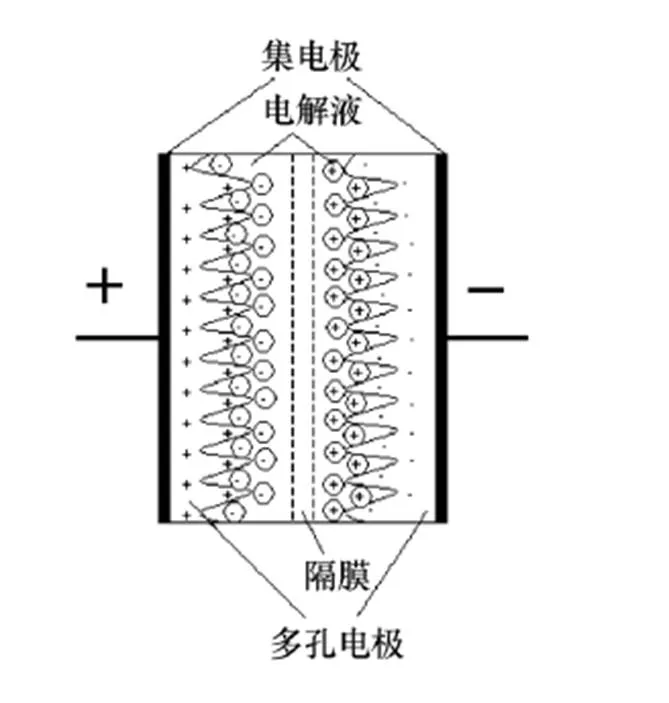
圖1 超級電容器的物理結構

1.2 多孔電極理論

電極和電解液是相對空間分布，需要用電容和電阻組成的復雜網絡來進行描述，而不是用簡單的理想電容。因為存在多孔性以及電極混合物的一些特殊性質，會出現由擴散元件表示的擴散現象[11]。擴散現象是由于歐姆性顆粒的接觸電阻及一些雜質引起了化學反應而生成了漏電阻。

Levie提出的電容器多孔電極模型[11]顯示，導體與電解液（液體與固體）接觸面的電荷是符號相反的雙層電荷，圖2所示為微觀描述多孔結構，其原理是依據流過多孔結構的傳輸電流的類型。電流可以分為三種：電解液與導體分界面的位移電流、電解液的離子運動形成的電流以及流過電極的電流[10]。

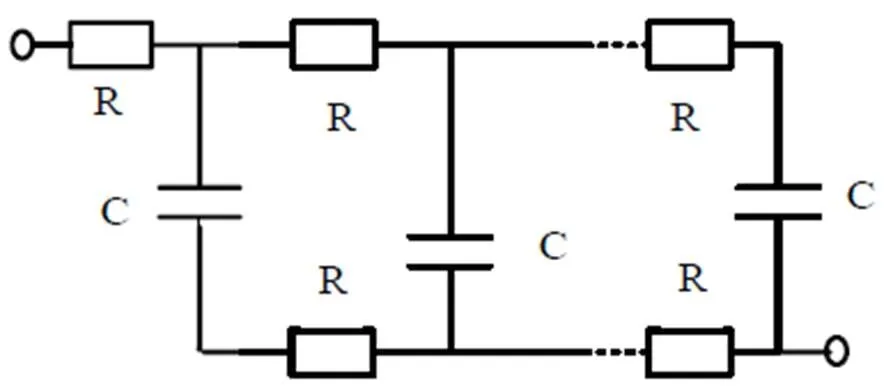
圖2 微觀描述多孔結構

1.3 等效電路模型

多分支RC參數模型[12]如圖3所示，此模型在充電放電過程的不同時間段每個分支單獨作用，即該模型的每個分支的時間常數不同且差別較大。分支1對超級電容器充電后前幾秒時間的瞬時響應具有決定作用且其時間常數較小；分支2對超級電容器在分鐘數的瞬時響應具有決定作用且其時間常數較大；分支3對超級電容器在10 min以上時間段的瞬時響應具有決定作用且其時間常數最大。提高該模型的分支數可以提高仿真精度。由于模型仿真精度和復雜度的矛盾性，通常情況下采用三分支模型。多分支RC參數模型基于電壓和電容的關系，描述超級電容器電荷重分配的過程更便捷，但由于該模型下每個分支的時間常數的確定在一定程度上需依據經驗，并且不同分支的時間常數較為獨立，這與實際情況有所不同。由于超級電容器一般工作于低頻，且在高頻時電感參數值較小，因此基本的等效電路模型不再考慮電感。

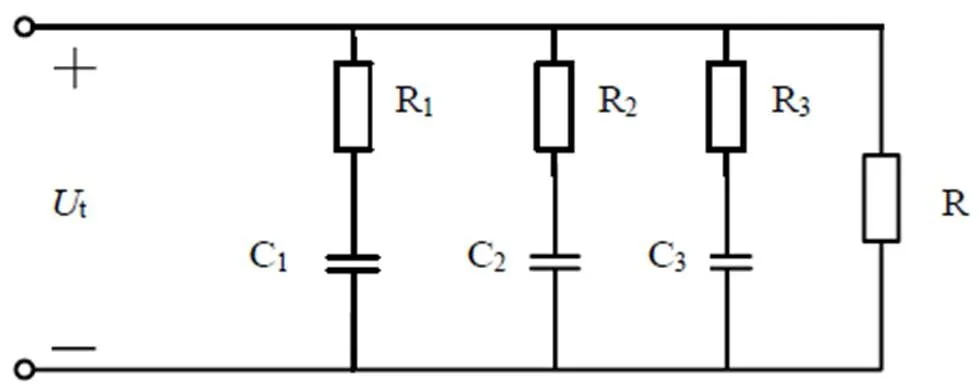
圖3 多分支RC參數模型

1.4 超級電容器頻域模型

通過阻抗譜分析的方法，得到超級電容器頻域模型。超級電容器的奈奎斯特圖如圖4所示[13]，在低頻段近似一條垂線，中頻段近似為45°的斜線。得出其低頻特性可以用一個理想電容來進行描述，在中頻段可以用一個純電阻來描述超級電容器多孔電極的復阻抗特性，超級電容器在高頻段具有電感特性。該模型中i表示串聯電阻，i表示多孔電極的復阻抗特性，表示超級電容器的高頻特性，但其在一般情況下可以忽略不計。

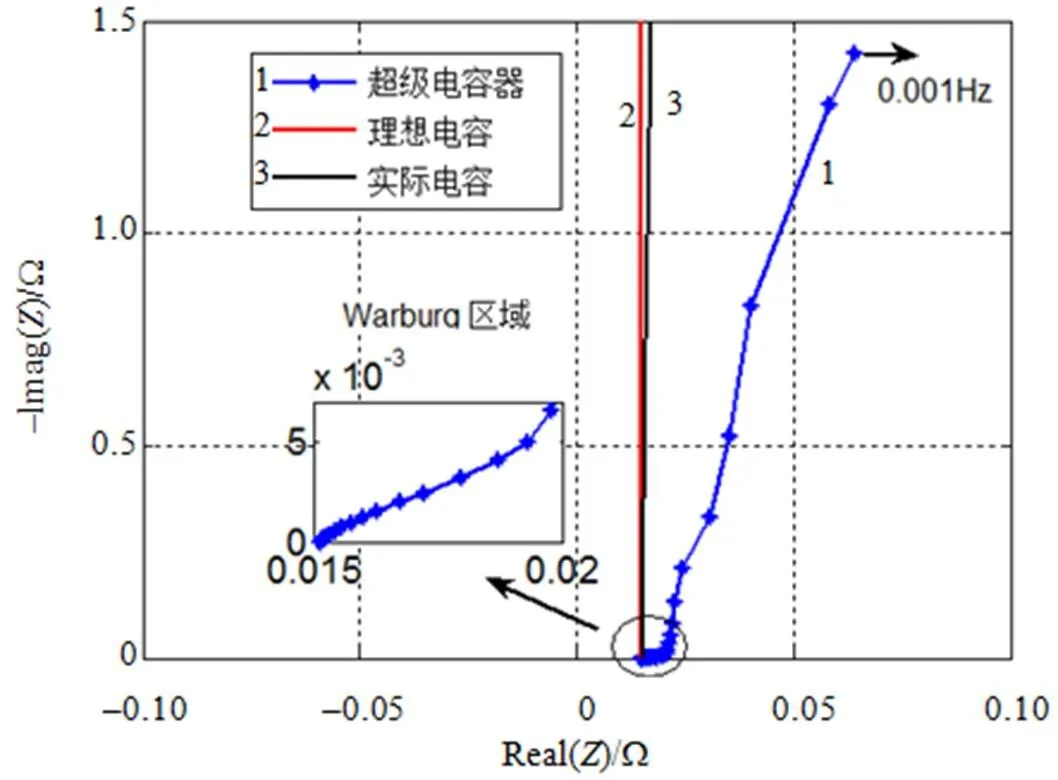
圖4 超級電容器奎納斯特圖

頻域模型的數學表達式如式(1)所示，其中e1和d1是多孔電極結構決定的阻容參數。

在頻帶較寬的情況下，超級電容頻域模型可以更精準地描述其頻率響應特性。

2 分數階巴特沃斯濾波器——超級電容器的無源實現

2.1 等分數階巴特沃斯低通濾波器

分數階巴特沃斯低通濾波器的頻率響應是平坦的通帶。特征方程的幅值平方函數為，其中為正整數表示濾波器的階數，表示歸一化頻率，表示通帶的衰減。

一般的分數階低通濾波器的傳遞函數如式(2)所示，其中, b為分數階階次并滿足>0，≤2。當=j時，傳遞函數的特征方程化簡為式(3)。

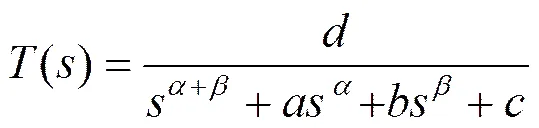
（3）

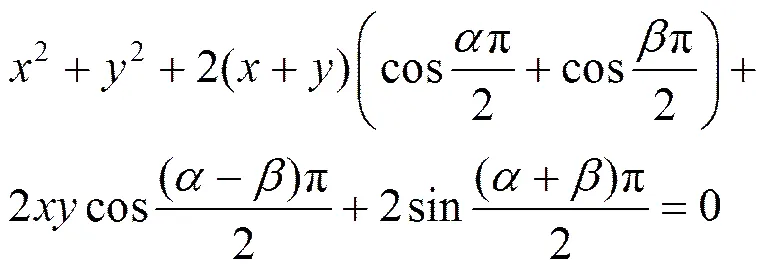
（5）

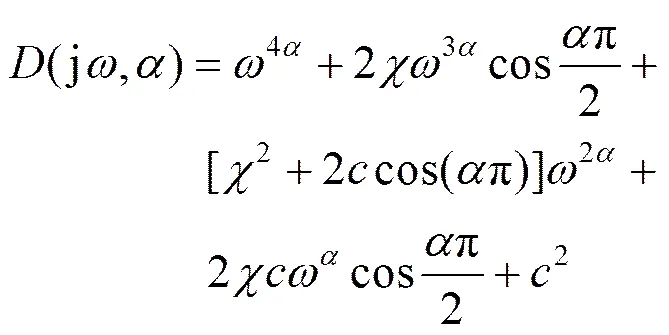
因此，一些簡化后的巴特沃斯低通濾波器條件為式(7)，其中，由此可知截止頻率與參數有關：。

（7）

Soltan和Radwan給出了對于等分數階巴特沃斯低通濾波器所要滿足條件下參數的關系如式(8)(9)，其中是關于條件方程解的情況而分為三類：無根、單根、雙根。

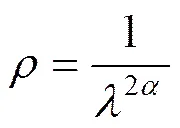
（9）

因此如果分數階次給定，則很容易得到巴特沃斯低通濾波器所滿足的條件。如圖5所示為階次時的幅值響應。

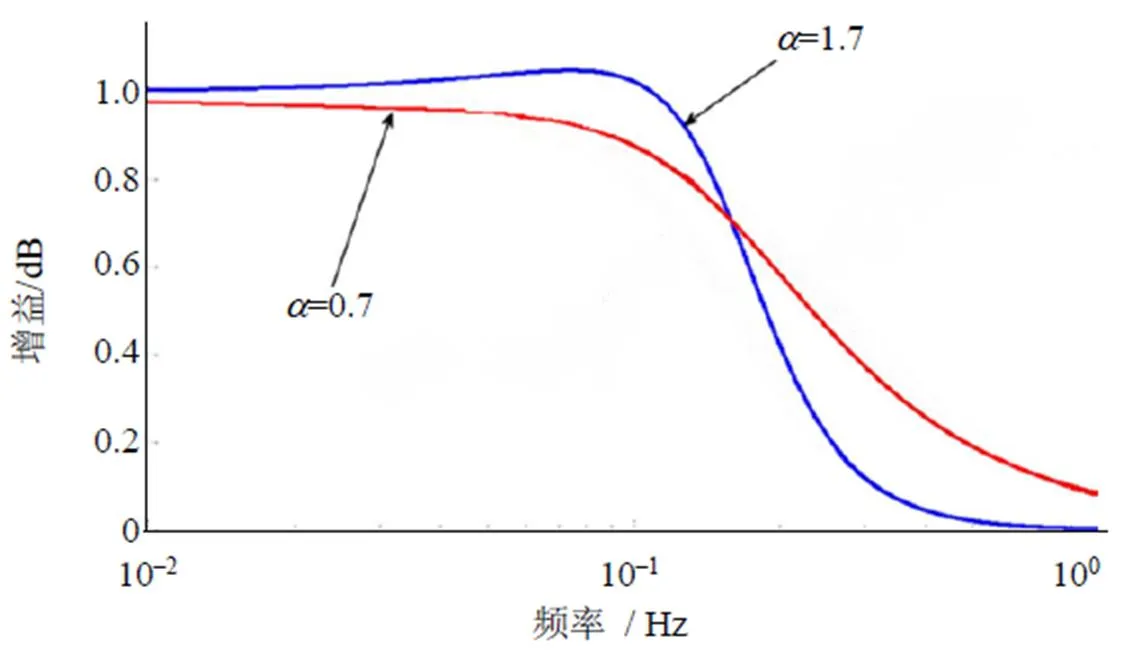
圖5 的濾波器幅值響應

2.2 新型超級電容器的無源實現

無源電路的傳遞函數與前面提到的類似，可以利用特殊情況下的算法來計算傳遞函數的相關參數。Kerwin–Huelsman–Newcomb（KHN）和Sallen–Key得出了傳遞函數中的參數與電路元器件的關系如式(10)所示。使用兩個具有不同分數階階次的元件實現的分數階巴特沃斯低通濾波器電路原理圖和電路仿真分別為圖6，圖7。使用兩個分數階元件的KHN濾波器無源實現如圖8所示。在不同分數階和等分數階階次的電路仿真如圖9所示。

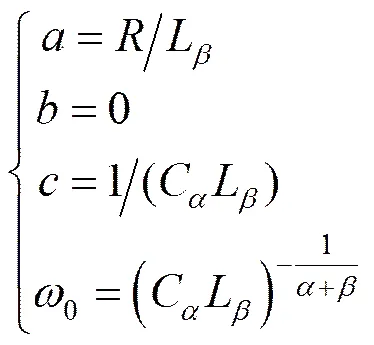
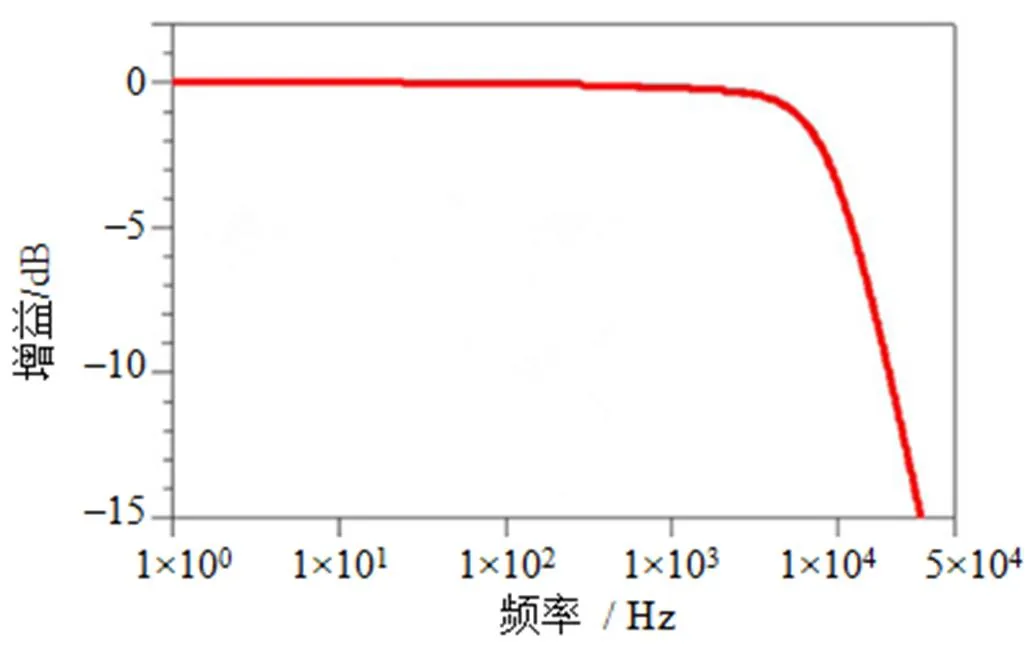
圖7 分數階巴特沃斯濾波器的電路仿真

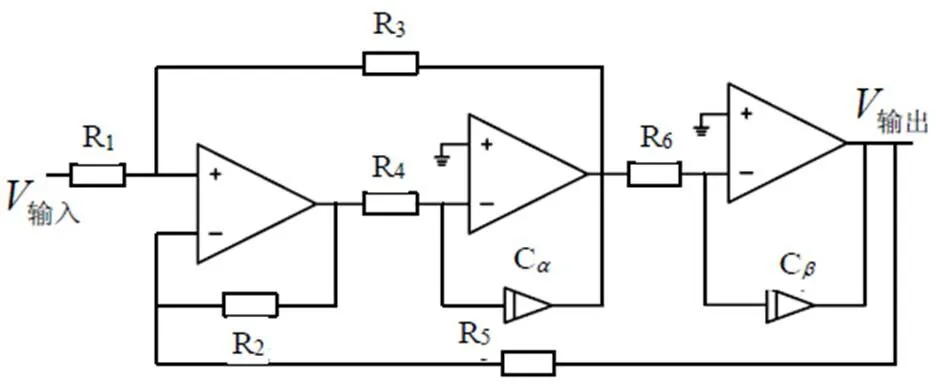
圖8 使用兩個不同分數階元件的KHN濾波器

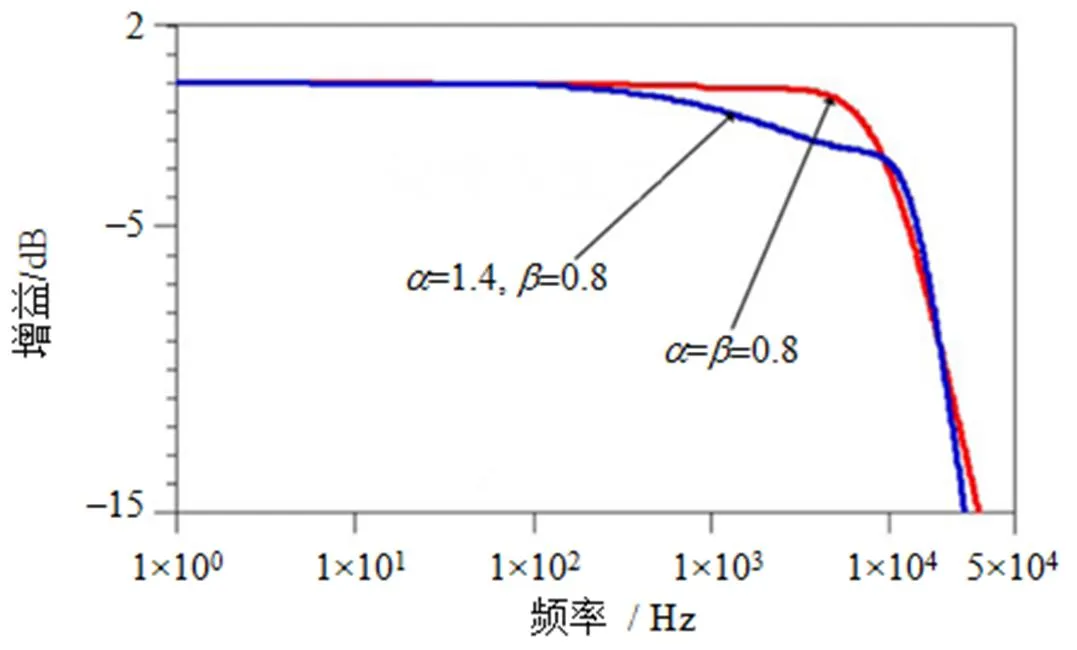
圖9 KHM濾波器電路仿真

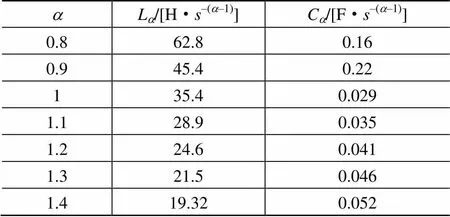
表1給出了在歸一化頻率h= 1 rad/s的條件下，當電阻= 50W時電容和電感的一些參數值。可以利用傳遞函數中參數與電路元件值的關系來得到無源電路的傳遞函數。此外，通過頻率縮放，電容參數和電感參數可以從任意截止頻率得到。

表1 在=50W, w0=1 rad/s時不同階次電容電感值

Tab.1 Values of L and C for differentat R=50 W, w0=1 rad/s

Tab.1 Values of L and C for differentat R=50 W, w0=1 rad/s

aLa/[H·s–(a–1)]Ca/[F·s–(a–1)] 0.862.80.16 0.945.40.22 135.40.029 1.128.90.035 1.224.60.041 1.321.50.046 1.419.320.052

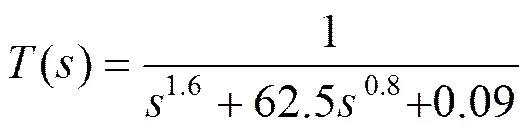
一種基于巴特沃斯低通濾波器的超級電容器如圖10所示，對于三階非線性超級電容部分，由之前討論可知每條分支時間常數都不同，該模型引入了受控電容和固定電容并聯的模式來更好地描述電容受端電壓的影響特性。其中引入的漏電阻是為了體現其自放電現象[12]。

圖10 超級電容器模型

Fig.10 Model of supercapacitor

此外，分數階超級電容器比整數階超級電容器具有更高的精度，而且分數階元件具有的傳輸特性可以更好解決在整數階超級電容器中支路數較多所帶來的問題[15]。利用部分分式展開的思路，運用矢量匹配的方法得到分數階超級電容器的表達式(12)。

其中每項如式(13)、(14)、(15)所示。

（13）

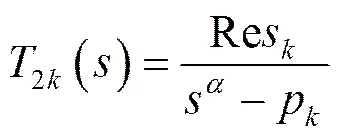
（15）

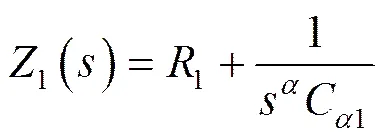
（17）

（18）

對比可得等效電路的參數為：

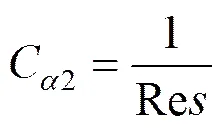
（20）

（21）

（23）

（24）

一種新型等分數階巴特沃斯濾波器-超級電容器等效模型如圖11所示，結合了基本模型與等分數階巴特沃斯濾波器。基本模型利用矢量匹配的結果用電路綜合的形式來實現[16]。這種超級電容器，可以接受更高更寬頻率的輸入量，同時也降低了模型的階數。

圖11 巴特沃斯濾波器-超級電容器模型

圖11所示阻抗如下所示：

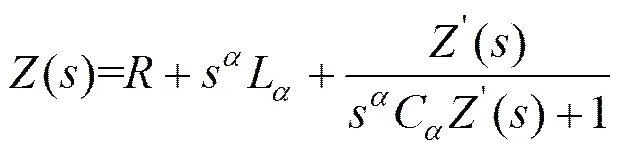
（26）

3 算例

為驗證本文所提新型超級電容器模型的合理性，考慮對2.7V 100F及16V 58F的超級電容器進行算例分析。圖12，13分別為2.7V 100F及16V 58F超級電容器的復頻相頻特性曲線[13]。

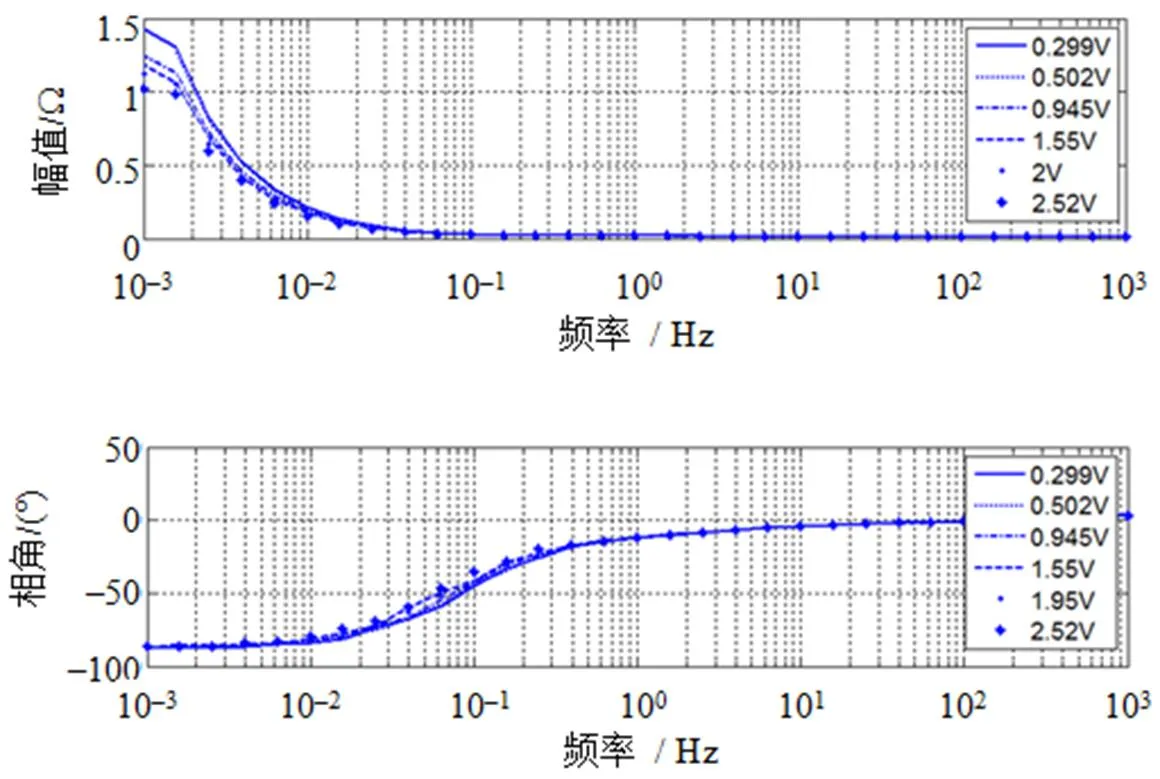
圖12 2.7V 100F超級電容的復頻相頻特性曲線

圖13 16V 58F超級電容的復頻相頻特性曲線

對于型號為2.7V 100F的超級電容器，其矢量匹配擬合后的阻抗為式(27)。考慮階次為的等分數階階次濾波器部分，其對應的參數值可以通過表1得到，即。最后代入(25)式可以得到阻抗。如圖14所示為阻抗的bode圖。

（28）

圖14 阻抗的頻率響應特性曲線

Fig.14 Frequency response curve of impedance

對于型號為16V 58F的超級電容器，其矢量匹配擬合后的阻抗為式(29)。考慮階次為的分數階階次濾波器部分，其對應的參數值可以通過表1得到，即。最后代入式(25)可以得到阻抗。如圖15所示為阻抗的bode圖。

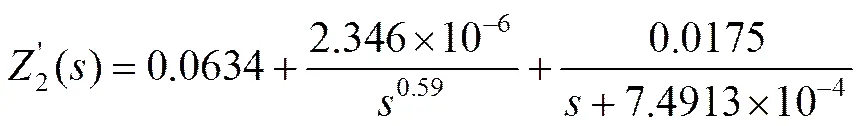
（30）

4 結論

基于超級電容器的基本等效電路模型，提出了分數階巴特沃斯濾波器的新型超級電容器模型，得到了模型的等效電路，并驗證了模型的準確性。擴充了超級電容器的基本模型理論，增大了其適用范圍，提高了抗噪能力。此外，可以在不改變電路結構和元器件的基礎上，利用改變濾波器的極點和帶寬來改變分數階階次，這樣大大增加了超級電容器的應用范圍與適用廣度。后續在研究超級電容器建模的基礎上，試探其他電子元件的分數階建模，這可以完善元件材料的理論體系，拓寬元件材料應用范圍，具有較好的現實意義。

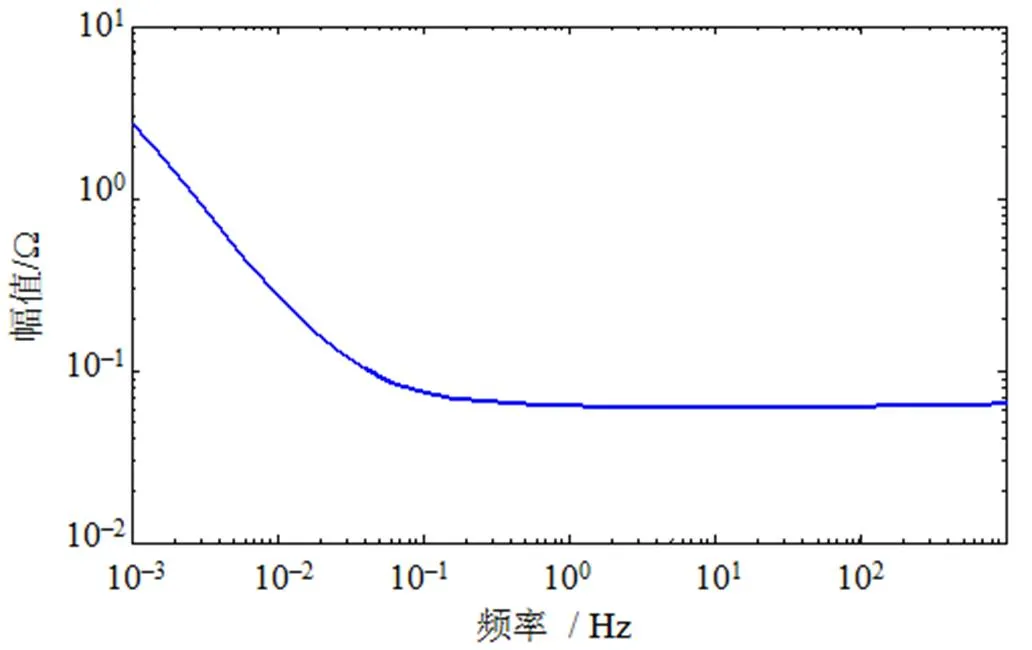
（a）幅值

（b）相角

圖15 阻抗的頻率響應特性曲線

Fig.15 Frequency response curves of impedance

[1] ASHTIANI C, WRIGHT R, HUNT G. Ultracapacitors for automotive applications [J]. J Power Sources, 2006, 154(2): 561-566.

[2] K?TZ R, CARLEN M. Principles and applications of electrochemical capacitors [J]. Electrochim Acta, 2000, 45(15/16): 2483-2498.

[3] SPYKER R L, NELMS R M. Classical equivalent circuit parameters for a double-layer capacitor [J]. IEEE Trans Aerospace Electron Syst, 2000, 36(3): 829-836.

[4] GUALOUS H, BOUQUAIN D, BERTHON A. Experimental study of supercapacitor serialresistance and capacitance variations with temperature [J]. J Power Sources, 2003, 123: 86-93.

[5] BROUJI H, BRIAT O, VINNASA J M, et al. Analysis of the dynamic behavior changes of supercapacitors during calendar life test under several voltages and temperatures conditions [J]. Microelectron Reliab, 2009, 49: 1391-7.

[6] 余水寶. 一種實現偶數高階濾波網絡的新方法[J].電子測量與儀器學, 1999, 13(1): 40-44.

[7] 陳三風. 一種新型的巴特沃斯低通濾波器設計[J]. 深圳信息職業技術學院學報, 2011(1): 89-92.

[8] JONSCHER A K. Dielectric relaxation in solids [M]. London: Chelsea Dielectric Press, 1983.

[9] 陳永真. 電容器及其應用[M]. 北京: 科學出版社, 2005: 202-203.

[10] 趙洋, 梁海泉, 張逸成. 電化學超級電容器建模研究現狀與展望[J]. 電工技術學報, 2012, 27(3): 188-195.

[11] Electrochemical supercapacitors: scientific fundamentals and technological applications [M]. New York: Kluwer Academic Plenum Press, 1999.

[12] ZUBIETA L, BONERT R. Characterization of double-layer capacitors for power electronics applications [J]. IEEE Trans Ind Appl, 2000, 36(1): 199-205.

[13] CHENG X, LIANG G S, LIU X, et al. A new supercapacitors fractional order nonlinear model [J]. Adv Mater Res, 2013(860/861/862/863): 2279-2282.

[14] 程序. 超級電容器分數階建模及其控制方法研究[D]. 保定: 華北電力大學, 2014.

[15] RIU D, RETIERE N, LINZEN D. Half-order modelling of supercapacitors [C]// Industry Applications Conference, 2004, 39th IAS Annual Meeting. New York: IEEE, 2004.

[16] 張世演. 網絡理論-模擬網絡及其應用 [M]. 成都: 西南交通大學出版社, 1993.

（編輯：曾革）

New supercapacitor modle of fractional order Butterworth filter

WANG Yan, CUI Jiantao, LIU Zhong

(College of the Electrical Engineering &Control Engineering, Liaoning Technical University, Xingcheng 125100, Liaoning Province, China)

Supercapacitors have broad application prospects in various fields as a new type of energy storage devices. It is important to establish an accurate and widely applicable model for the inherent characteristics of supercapacitors are not integer order. The basic model of supercapacitor was introduced. Based on the fractional Butterworth filter, a new type of model was proposed and the accuracy of the model was verified. This can expand the scope of application and improve the stability for the supercapacitor.

supercapacitor; modeling; fractional order; Butterworth filter; equivalent circuit model; stability

10.14106/j.cnki.1001-2028.2017.05.007

TM53

A

1001-2028（2017）05-0030-07

2017-01-06

崔建濤

王焱（1970－），女，遼寧阜新人，教授，主要從事信號檢測與處理研究，E-mail: 179577221@qq.com ；崔建濤（1990－），男，山西臨汾人，研究生，研究方向為電力系統及其自動化，E-mail: 764343289@qq.com；劉忠（1968－），男，遼寧葫蘆島人，研究方向為供電技術，E-mail: 532292835@qq.com 。

網絡出版時間：2017-05-11 13:24

http://kns.cnki.net/kcms/detail/51.1241.TN.20170511.1324.007.html