基于Lyapunov優化的時變無線傳感網路由研究*
董齊芬,張其前
(浙江警察學院計算機與信息技術系,杭州 310053)
?
基于Lyapunov優化的時變無線傳感網路由研究*
董齊芬*,張其前
(浙江警察學院計算機與信息技術系,杭州 310053)
針對無線傳感網應用中監測環境具有隨機性和不可預測性等因素使得節點感知速率通常是時變的且某些時刻會超出鏈路容量的實際問題,設計了一種時變路由算法。在該算法中,將時變感知速率下的路由問題建立成以時均的網絡能耗與丟棄感知數據代價的加權和最小為目標的隨機優化模型,并利用Lyapunov優化技術求解該模型,進而得到一種路由策略來實時決策每條鏈路上的數據流量以及由于節點感知速率持續超出鏈路容量而不得不丟棄的數據量。進一步,討論感知數據不被丟棄的條件,建立目標函數與感知信息最大傳輸時延之間的權衡關系。最后,通過仿真實驗,驗證了本文算法在能耗、感知數據的丟棄量及傳輸時延之間的均衡關系。還在不同的最大數據感知速率下,比較了本文算法與AVE算法的性能。
無線傳感器網絡;時變路由;Lyapunov優化
無線傳感器網絡WSNs(Wireless Sensor Networks)作為物聯網的“末梢神經”,是一種綜合信息采集、處理和傳輸功能于一體的新型網絡信息系統,在環境監測、智慧城市、公共安全等領域有著廣泛應用前景。但通常地,WSNs節點的能量、通信距離和鏈路容量等資源均是受限的。在滿足鏈路容量等有限資源約束的前提下,如何設計能量有效的路由機制一直以來都是WSNs研究熱點之一[1]。
目前,基于能量有效的路由研究已取得一定成果。其中,將最大化WSNs生存周期的路由問題直接建模或轉換成線性規劃模型并采用經典的最優化法或最短路徑樹、人工智能等方法求解的研究思路受到了學者們的青睞。文獻[2]是較早用線性規劃模型表示網絡生存周期最優路由問題的典型代表作。該模型考慮了流量平衡約束和能耗約束,并采用次梯度算法實現分布式求解。在此基礎上,不少學者進一步考慮實際條件,對這類問題深入研究[3-7]。如文獻[3]考慮WSNs中有多個Sink節點的情況,并將多個Sink節點的數據收集路由問題分解成若干個單個Sink節點的路由問題,從而建立優化網絡生存時間的路由模型;文獻[4]在文獻[2]模型的基礎上增加了鏈路的帶寬資源約束;針對節點的位置不平等造成節點能耗不均衡從而在一定程度上減低了網絡生存時間的問題,文獻[5-7]采用Sink節點移動的方法解決。他們在求解最優路由的同時優化Sink節點的移動路徑或移動Sink節點在每個位置的停留時間。最近,還有學者研究如何根據節點剩余能量、節點度及鄰居節點狀態等參數來自適應調節路由以均衡節點能耗[8-9]。
上述成果為能量有效的路由機制提供有力的理論支撐,但大部分認為節點感知速率是常量。然而在實際應用中,由于監測環境具有隨機性,節點感知速率通常是時變的。文獻[10-12]雖然對時變感知速率問題進行了研究,但其前提是節點的平均感知速率是已知的。在具有隨機性和不可預測性的監測環境中,節點的平均感知速率也是很難獲取的。本文對此問題進一步深入研究,設計一種時變路由算法。該算法還考慮了節點感知速率超出WSNs鏈路容量時的特殊情況。主要貢獻歸納為:①考慮WSNs應用中監測環境具有隨機性和不可預測性等實際因素,將時變感知速率下的路由問題建立成以時均的網絡能耗與丟棄感知數據代價的加權和最小為目標的隨機優化模型;②利用解決無線網絡中的隊列系統動態控制問題的Lyapunov優化技術[13],設計一種時變路由算法;③討論感知數據不被丟棄的條件,建立網絡能耗與感知信息的最大傳輸時延之間的權衡關系;④通過仿真實驗來驗證本文提出的時變路由算法的可行性和有效性,并與基于平均感知速率的路由算法進行比較。
1 問題描述與建模
用G(V,L)表示一個無向連通的無線傳感器網絡,其中,V是所有節點的集合,包含N個傳感節點和1個Sink節點,L是所有無線鏈路的集合。設Pmax為允許的節點最大發射功率,如果節點i和節點j之間進行無線通信所需的發射功率小于Pmax,那么稱節點i流向節點j的無線鏈路lij∈V存在,且無線鏈路是雙向存在的(但Sink節點沒有出鏈路),節點i和節點j相互稱為鄰居節點。令Ni表示節點i的所有鄰居節點的集合。為方便敘述與分析,再作如下定義與假設:
①傳感節點同時承擔數據采集和中繼任務。
②傳感節點的能耗主要用于收發數據,忽略數據感知、計算等能耗。

式中:dij表示節點i與節點j之間的距離,Eelec代表收發單位比特數據時的電路電子能耗,εfs是放大單位比特數據時所需要的電子能耗。
④無線鏈路的帶寬資源是有限的,設單位時間內每條鏈路上的最大數據傳輸量為Rmax。
⑤由于WSNs應用中的監測環境具有隨機性和不可預測性,故不同節點在單位時間內的數據感知量均不同且是隨機的。令節點i在時間t的數據感知量為ai(t),且有amin≤ai(t)≤amax,其中的amin和amax分別表示節點在單位時間內的最小和最大數據感知量。
由于傳感節點的數據感知速率隨機可變,且無線鏈路的帶寬資源受限,故無法保證當前時間內的所有感知數據都能發送到Sink節點。為了利用帶寬資源受限的無線鏈路將感知信息在允許的收集時延要求內傳輸到Sink節點,本文首先將每個節點的感知數據存儲在相應隊列中,然后通過一定的策略進行處理。具體地,令Qi(t)為節點i的感知數據存儲隊列在時間t的存儲量,且根據下式更新:
Qi(t+1)=max{Qi(t)-ρi(t)-bi(t),0}+ai(t), ?i,t
(1)
式中:Qi(0)=0;ρi(t)≥0和bi(t)≥0是需要決策的變量,其中:ρi(t)表示在時間t發送出去的關于節點i的感知數據量。為使得當前發送出去的數據能被Sink節點接收到,每個傳感節點應滿足數據流量平衡約束:
(2)
式中:γij(t)≥0表示在時間t節點i發送給其鄰居節點j的數據量。因為單位時間內每條鏈路上的最大數據傳輸量是有限的,所以γij(t)應滿足如下約束:
γij(t)+γji(t)≤Rmax,?lij∈L且j≠Sinkk節點
γij(t)≤Rmax,j=Sink節點
(3)
bi(t)表示當出現傳感節點的感知速率持續超出鏈路容量的特殊情況時不得不丟棄的數據量。用單調遞增的凸函數c(x)=α(x2+x)來表征丟棄感知數據的代價,其中α是可調系數。該代價函數表明當α給定時,丟棄的感知數據越多,對整個應用系統的影響越大,且隨著丟棄數據量的增加,其影響更是急劇增大的。為防止丟棄過多數據量從而破壞系統性能,令單位時間內允許節點丟棄的最大數據量為bmax。
根據Lyapunov優化技術,為確保感知信息的收集時延是有限的,每個隊列應是可穩定的,即:
(4)
式中:E{·}表示數學期望。
隨著無線充電技術和智能移動節點的發展,可在WSNs中部署移動充電站為傳感節點提供高效及時的充電服務,以保證傳感節點持久正常地工作[14-15]。但是,這并不代表可以任意浪費節點能量,因此減少網絡能耗從而降低充電代價仍是WSNs研究中的重要指標。故本文目標是在滿足上述各項約束的前提下,合理決策ρi(t)、γij(t)及bi(t),使時均的網絡能耗與丟棄感知數據代價的加權和最小,即建立如下的隨機優化模型:
(5)
2 算法設計
可以采用動態規劃或馬爾科夫決策求解上述隨機優化模型,但前提是節點感知數據量的先驗統計信息是完全可知的。然而,對事件發生具有不可預測性的WSNs應用來說,這很難滿足。為此,本節引入解決無線網絡中的隊列系統動態控制問題的Lyapunov優化技術,設計一種可行有效的算法求解上述隨機優化模型,使得在任意時間t,只要根據當前觀測值,即可計算出ρi(t)、γij(t)及bi(t)。
2.1 預備知識
定義虛擬隊列:
Zi(t+1)=
max[Zi(t)-bi(t)-ρi(t)+δ1{Qi(t)>0},0], ?i,t
(6)
式中:Zi(0)=0;δ是可調參數,其取值影響感知數據的收集時延和隨機優化問題(5)的目標函數值;1{Qi(t)>0}是符號函數,當Qi(t)>0時,它為1,否則為0。首先,給出與感知信息傳輸時延有關的引理[13]。
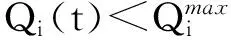
(7)
再記Θ(t)=[{Qi},{Zi}]為當前感知數據存儲隊列和相應虛擬隊列的向量,并定義二次型Lyapunov函數:
(8)
根據感知數據存儲隊列和相應虛擬隊列的更新式(1)和(6),有:
(9)
最后一個不等式由0≤bi(t)≤bmax得到。然后,定義一階Lyapunov平移函數Δ(Θ(t)):
Δ(Θ(t))=E{L(Θ(t+1))-L(Θ(t))|Θ(t)}
(10)
進一步,將隨機優化問題(5)的目標函數以懲罰項的形式與Lyapunov平移函數相加,得到以下的Lyapunov平移函數-加-懲罰函數:
(11)
式中:V是可調參數,其取值也會影響數據收集時延和隨機優化問題(5)的目標函數值。由式(9)可得:
(12)
2.2 算法實現
給出基于Lyapunov優化的WSNs時變路由算法,如表1所示。算法的實現遵循Lyapunov優化技術的基本思路,即選擇一種策略ρi(t)、γij(t)及bi(t),使得式(12)不等號右邊的表達式最小。

表1 基于Lyapunov優化的WSNs時變路由流程
2.3 算法性能分析
分析當感知數據量ai(t),?i服從獨立同分布時本文算法的性能。
定理1 若參數δ滿足0<δ≤E{ai(t)},?i,且bmax≥amax,那么,提出的算法具有以下特性:
①在任意時間t內,節點i的感知數據存儲隊列及相應的虛擬隊列均滿足:
Qi(t)+Zi(t)≤Ωmax, ?i
(15)
式中:Ωmax=Vα+2bmax(Vα+1)+amax。
②感知數據的最大收集延時為:
(16)
③對?t,若節點i均有Qi(t)+Zi(t)≤Vα-δ時,則節點i的感知數據不會被丟棄。
④令ρi(t)、γij(t)及bi(t)是根據算法1計算的值,φ是相應的時均網絡能耗和丟棄感知數據代價的加權和。那么,φ與隨機優化問題(5)的最優目標函數值φopt之間滿足:
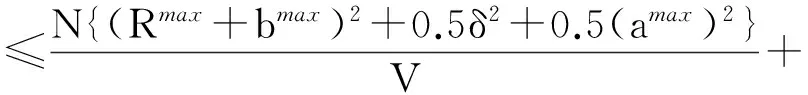
(17)
證明 ①用數學歸納法證明。顯然Qi(0)+Zi(0)=0<Ωmax。假設當t=s時,命題成立,即Qi(s)+Zi(s)≤Ωmax。下面證明當t=s+1時,命題仍成立。
首先,分析Qi(s)+Zi(s)≤Vα+2bmax(Vα+1)-δ的情況。根據式(1)和式(6)可知,更新Qi(s)和Zi(s)時,它們的增加量分別不會超過amax和δ,故有Qi(s+1)+Zi(s+1)≤Qi(s)+Zi(s)+amax+δ≤Ωmax。
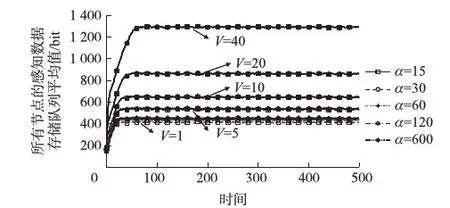
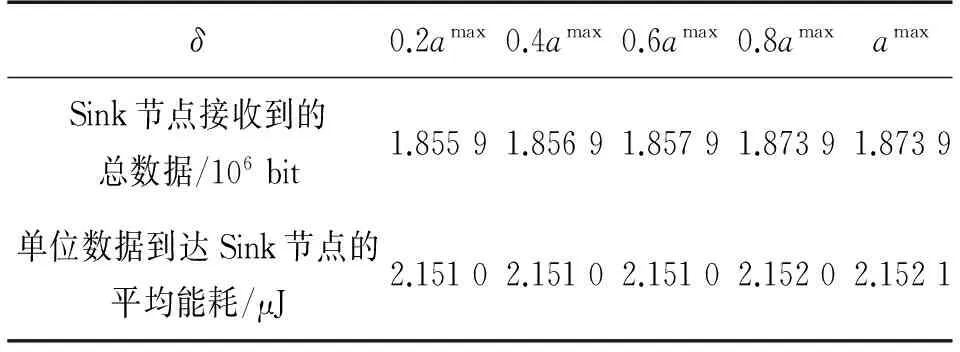
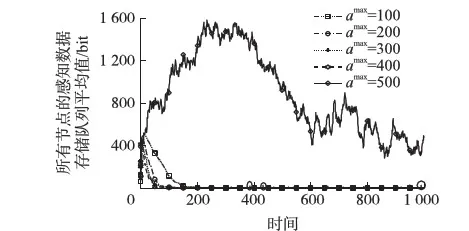
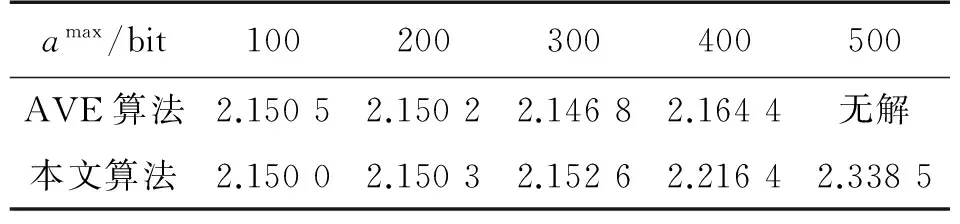
再分析Vα+2bmax(Vα+1)-δ δ+Qi(s)+Zi(s)>Vα+2bmax(Vα+1) (18) 令算法1的第2步中的子項為: fi(bi(t))=Vc(bi(t))+bi(t)2-bi(t){Qi(t)+δ+Zi(t)} 則fi(bi(t))在0≤bi(t)≤bmax處的一階導數滿足: Vα(2bi(t)+1)+2bi(t)-{Qi(t)+Zi(t)+δ} (19) 上式表明當Vα+2bmax(Vα+1)-δ 綜上,Qi(t)+Zi(t)≤Ωmax, ?i成立。 ②將命題①的結果代入引理1即可。 ③當Qi(t)+Zi(t)≤Vα-δ時,fi(bi(t))在0≤bi(t)≤bmax處的一階導數滿足: Vα(2bi(t)+1)+2bi(t)-{Qi(t)+Zi(t)+δ}≥0 上式表明當Qi(t)+Zi(t)≤Vα-δ時,fi(bi(t))在區間[0,bmax]上是單調遞增的,故計算出bi(t)=0,即節點i的感知數據不會被丟棄。 (20) (21) 然后,根據本文提出的算法原則,即選擇一種策略ρi(t)、γij(t)及bi(t)使得式(12)不等號右邊的表達式最小,可得: (22) 式中:第3個不等式根據式(20)和式(21)、ε→0及0<δ≤E{ai(t)},?i得到;第4個不等式根據0≤bi(t)≤bmax、0≤ρi(t)≤Rmax和0≤ai(t)≤amax得到;最后一個等式是由bmax、Rmax和amax及δ均為常數得到。將Φ(t)的表示式(11)代入上式,然后在式的兩端取數學期望,則由迭代期望法則可得: (23) 再將上式兩端除以TV,并從t=0到t=T-1依次相加,得: (24) 因為Qi(t)和Zi(t)有界,所以L(Θ(t))有界。因此,令T→∞時可得: (25) 綜上,4個命題全部得證。 可見,當感知數據量ai(t),?i服從獨立同分布時,本文提出的算法使目標函數值與感知信息的最大收集時延存在一定的均衡關系,即感知信息的最大收集時延與V和1/δ成正比,而目標函數值與1/V和δ成正比。另外,由命題③可知,只要傳感節點的數據感知速率不持續超出WSNs鏈路容量,通過設置合理的代價函數c(·)就能保證感知數據不會被丟棄,且在能耗與最大收集時延之間達到均衡。 3.1 仿真設置 為了驗證本文提出的時變路由算法的可行性和有效性,本部分對算法進行仿真,仿真在MATLAB平臺上進行。假設25個節點隨機部署于500 m×500 m的正方形區域內,仿真區域的中心位置布置一個Sink節點,節點間的最大通信距離是140 m。本文產生的WSNs拓撲結構如圖1所示。仿真中用到的其他共同參數:節點i在時間t的數據感知量ai(t)在區間[amin,amax]上隨機產生;發送單位比特數據時電路電子能耗Eelec=50 nJ/bit;放大單位比特數據時所需要的電子能耗εfs=100 pJ/(bit/m2);單位時間內鏈路允許的最大傳輸量Rmax=1 000 bit;單位時間內允許節點丟棄的最大數據量bmax=amax。 圖1 本文產生的WSNs拓撲結構 (26) 3.2 參數V與α對算法的影響 設置節點在單位時間內的最小和最大數據感知量分別是amax=200 bit和amin=100 bit,參數δ=0.6×amax。隨著參數V和代價函數中的可調系數α的變化,感知數據存儲隊列、丟棄的總數據量、Sink節點接收到的總數據量及能耗等性能指標的變化分別如圖2~圖5所示。 圖2 參數V和α對感知數據存儲隊列的影響 圖3 參數V和α對丟棄的總數據量的影響 圖4 參數V和α對Sink節點接收到的總數據量的影響 圖5 參數V和α對能耗的影響 分析可得:①通過選取合適的V和α的值,保證了感知數據的丟棄量為0,且當α的值較大時,即提高丟棄感知數據的代價,較小的V值就能保證感知數據不被丟棄。如圖3所示,在此仿真環境下,當α≥60時,只要調節V的值使得Vα≥600,感知數據就不會被丟棄。②仔細觀察圖2、圖4和圖5,當V值給定且調節α的值使得保證感知數據不被丟棄時,再增加α的值對網絡的其他性能幾乎沒有影響。這表明在實際應用中,可以選取較大的α值,從而為V值的選取提供更大的范圍。③根據圖3~圖5,當丟棄的數據量越多,需要發送給Sink節點的數據量就越少,所以經過能耗大的路徑發送的數據量減少,從而使得發送單位數據到達Sink節點的平均能耗就降低。④隨著V的增加,發送單位數據到達Sink節點的平均能耗就減少,但其代價是所有節點的感知數據存儲隊列平均值增加,即增大了數據到達Sink節點的平均時延。這和第2部分的理論分析結果是一致的。 圖6 參數δ對感知數據存儲隊列的影響 3.3 參數δ對算法的影響 設置節點在單位時間內的最小和最大數據感知量分別是amax=200 bit和amin=100 bit,參數V=10及代價函數中的可調系數α=60。隨著參數δ從0.2amax增加到amax,得到:①感知數據的丟棄量均為0。這表明只要確定了合適的V值和α值,參數δ值的變化幾乎不會影響感知數據的丟棄情況;②如圖6所示,所有節點的感知數據存儲隊列平均值減少,即降低了數據到達Sink節點的平均時延。又由于數據丟棄量均為0,在500個單位時間處,Sink節點接收到的總數據量是不斷增多的,如表2中的第2行所示。特別地,當δ值增加到0.8amax時,穩定狀態下的所有節點的感知數據存儲隊列平均值為0,即所有數據均被實時傳輸到Sink節點。當然,其代價是相比于δ≤0.6amax時的情況,發送單位數據到達Sink節點的平均能耗增加了約0.001 μJ。 從上述分析可知,能耗、感知數據的丟棄量及傳輸時延之間存在一定的均衡關系。因此應根據實際需求來確定參數V、δ及α的值。 表2 參數δ對Sink節點接收到的總數據量和能耗的影響 圖7 不同的數據感知速率對感知數據存儲隊列的影響 3.4 本文算法與AVE算法的比較 設置節點在單位時間內的最小數據感知量是amin=0 bit,參數V=10、δ=0.6×amax及代價函數中的可調系數α=60,節點在單位時間內的最大數據感知量amax從100 bit逐步增加到500 bit。由圖7和表3可知,①當amax≤200 bit時,穩定狀態下的所有節點的感知數據存儲隊列平均值均為0,本文算法發送單位數據到達Sink節點的平均能耗略高于AVE算法;②當300 bit≤amax≤400 bit時,穩定狀態下的所有節點的感知數據存儲隊列平均值在大部分時間為0,但會出現小波動,如圖7中的黑色小圓圈所示。這是由于隨著數據感知速量的增加,能耗小的路徑上的鏈路承受力趨于飽和,本文算法試圖等待在感知數據量較少的時間里再將數據沿著能耗小的路徑傳輸到Sink節點,這正是本文算法的出發點之一,如第1部分所述。另外,本文算法發送單位數據到達Sink節點的平均能耗明顯高于AVE算法,尤其當amax=400 bit時,本文算法發送單位數據到達Sink節點的平均能耗增加了達0.052 μJ;③當amax增加到500 bit時,節點的感知量超出了WSNs鏈路容量,故AVE算法無法得到可行解,而本文算法通過等待和丟棄少量數據量等策略,使得Sink節點接收到了95.44%的感知數據。 表3 不同的最大數據感知速率下,發送單位數據 可見,本文算法在節點感知數據量較低的情況下,能得到接近于AVE算法的路由結果,同時也能處理節點感知數據量較高使得AVE算法無法計算的情況。但當節點感知數據量較為均衡時,本文算法的性能欠佳。不過再次說明,實際中節點的平均感知速率是很難得到的。 本文考慮WSNs應用中監測環境具有隨機性和不可預測性等因素,研究時變感知速率下的路由問題,提出了一種基于Lyapunov優化技術的時變路由算法來實時決策每條鏈路上的數據流量以及由于節點感知速率持續超出鏈路容量而不得不丟棄的感知數據量。理論分析與仿真實驗均表明通過選取合適的參數V、δ及α值,可在能耗、感知數據丟棄量及傳輸時延之間達到一定的均衡。本文算法還能處理節點感知速率較高使得AVE算法無法計算的情況。下一步將結合Sink節點移動的方法,進一步研究優化算法在能耗、感知數據的丟棄量及傳輸時延等方面的性能。 [1] 何杏宇,周亦敏,楊桂松,等. 無線傳感器網絡能量感知增強樹型路由協議研究[J]. 傳感技術學報,2015(4):551-556. [2] Madan R,Lall S. Distributed Algorithms for Maximum Lifetime Routing in Wireless Sensor Networks[C]//Proceedings of the IEEE Global Telecommunications Conference,2004:748-753. [3] Hong Y,Xu J,Jiang C. Lifetime Maximization in Wireless Sensor Networks with Network Coding[C]//Proceedings of IEEE International Conference on Wireless Communications,Networking and Mobile Computing,Los Angeles:IEEE,2007:2527-2530. [4] Cheng M,Gong X,Cai L. Joint Routing and Link Rate Allocation under Bandwidth and Energy Constraints in Sensor Networks[J]. IEEE Transactions on Wireless Communications,2009,8(7):3770-3779. [5] 任條娟,楊海波,陳友榮. Sink 節點移動的無線傳感網生存時間優化算法[J]. 傳感技術學報,2012,25(5):683-690. [6] Yun Y S,Xia Y,Behdani B,et al. Distributed Algorithm for Lifetime Maximization in Delay-Tolerant Wireless Sensor Network with Mobile Sink[J]. IEEE Transactions on Mobile Computing,2012,12(10):370-375. [7] Yun Y S,Xia Y. Maximizing the Lifetime of Wireless Sensor Networks with Mobile Sink in Delay-Tolerant Applications[J]. IEEE Transactions on Mobile Computing,2010,9(9):1308-1318. [8] Wang Y,Tan H. Distributed Probabilistic Routing for Sensor Network Lifetime Optimization[J]. Wireless Networks,2016,22(3):975-989. [9] Kumar V,Kumar S. Energy Balanced Position-Based Routing for Lifetime Maximization of Wireless Sensor Networks[J]. Ad Hoc Networks,2016,52:117-129. [10] 薛亮,王燕龍,李志華,等. 無線傳感器網絡中基于數據融合的時變速率路由算法[J]. 微電子學與計算機,2015,32(12):130-135. [11] Hou Y T,Shi Y Y. Variable Bit Rate Flow Routing in Wireless Sensor Networks[J]. IEEE Transactions on Wireless Communications,2007,6(6):2140-2148. [12] Xue L,Yang B,Zhao J,et al. Joint Resource Reconfiguration and Robust Routing for Cognitive Radio Networks:A Robust Optimization Approach[J]. Wireless Communications and Mobile Computing,2015,15(5):848-867. [13] Neely M J. Stochastic Network Optimization with Application to Communication and Queuing Systems[M]. Morgan & Claypool,2010. [14] Yuanyuan Y,李亞寧. 無線可充電傳感器網絡[J]. 國外科技新書評介,2015(7):22-23. [15] 胡誠,汪蕓,王輝. 無線可充電傳感器網絡中充電規劃研究進展[J]. 軟件學報,2016,27(1):72-95. Variable Bit Rate Flow Routing in Wireless Sensor Networks Based on Lyapunov Optimization* DONG Qifen*,ZHANG Qiqian (Department of Computer and Information Technology,Zhejiang Police College,Hangzhou 310053,China) Monitoring environment in the application of wireless sensor networks is always random and unpredictable,so the node sensing rate is usually time-varying and may exceed the link capacities at some time-slots. Pointing at this problem,a variable bit rate flow routing algorithm is designed in this paper. In the proposed algorithm,the routing problem with time variable sensing rate is described as a stochastic optimization model whose objective function is to minimize the weighted sum of time-average power consumption and the cost induced by discarding sensed data. The model is solved by Lyapunov optimization technique,and a routing method is proposed to determine the amount of data flowing through each link and to calculate the amount of data to be discarded when the node sensing rate continuously exceeds the link capacities in real time. Further,the condition under which the data will not be discarded is discussed and an explicit trade-off between the value of objective function and the worst-case delay of data transmission is obtained. Finally,simulation demonstrates the relationship among power consumption,the amount of discarded data and the data transmission delay. We also compare the performance of the proposed algorithm with AVE algorithm under different maximum node sensing rates. wireless sensor networks;variable bit rate flow routing;lyapunov optimization 董齊芬(1985-),女,博士,講師,主要研究方向為無線傳感網、優化算法,dongqifen@zjjcxy.cn; 張其前(1976-),男,博士,講師,主要研究方向為計算機取證,控制理論、優化理論等。 項目來源:NSFC-浙江兩化融合聯合基金項目(U1509219) 2016-11-03 修改日期:2016-12-29 TP393 A 1004-1699(2017)05-0758-08 C:7230 10.3969/j.issn.1004-1699.2017.05.021
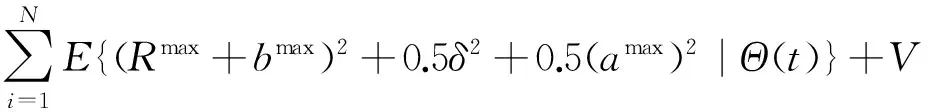
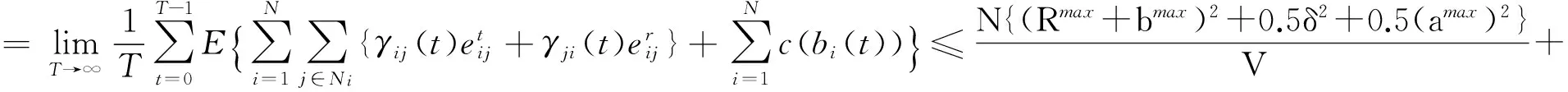
3 仿真實驗

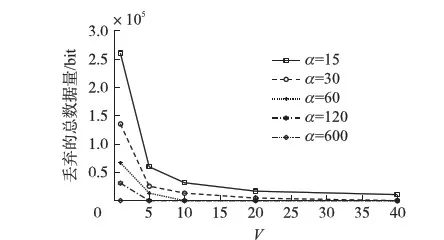
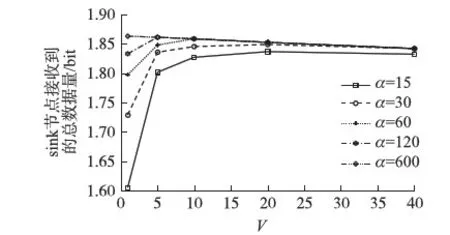
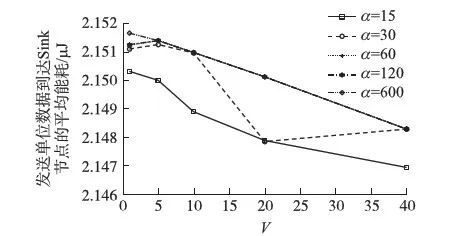
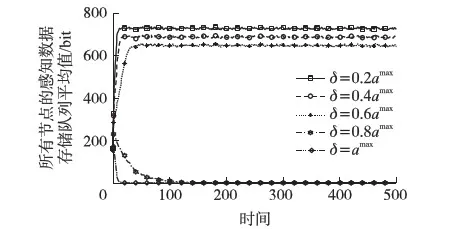
4 結語



