陀螺漂移誤差建模與濾波*

李 杰,鄭倫貴,2*,王建中

(1.中北大學儀器科學與動態測試教育部重點實驗室,太原 030051;2.清華大學精密測試技術及儀器國家重點實驗室,北京 100084)

?

陀螺漂移誤差建模與濾波*

李 杰1,鄭倫貴1,2*,王建中1

(1.中北大學儀器科學與動態測試教育部重點實驗室,太原 030051;2.清華大學精密測試技術及儀器國家重點實驗室,北京 100084)

MEMS陀螺漂移誤差直接影響光電穩定跟蹤平臺伺服機構的控制精度。針對MEMS陀螺隨機漂移誤差慢時變、弱非線性、難以準確補償的特點,基于隨機序列時序分析法的基本原理,對預處理后的MEMS陀螺漂移殘差信號進行建模,并根據模型對殘差信號進行Kalman濾波。結果顯示濾波前后信號的方差提高了1到2個數量級,表明有效抑制了漂移誤差,提高了MEMS陀螺的精度。

MEMS陀螺;隨機漂移;時間序列分析;Kalman濾波

光電穩定跟蹤平臺因其能隔離載體運動對載荷的干擾,在現代武器系統和民用設備中得以廣泛應用。作為其關鍵部件,MEMS陀螺的測量誤差將直接影響穩定平臺的穩定精度。MEMS陀螺的系統誤差可通過數學模型得以準確補償,而隨機漂移誤差具有慢時變、弱非線性的特點[1],其長時間的誤差積累將嚴重污染姿態角的量測結果,故降低MEMS陀螺的隨機漂移誤差能夠有效改善陀螺的性能,從而提高穩定平臺的精度。小波分析難以選取合適的小波基及變換尺度[2-6],神經網絡法存在訓練時間長、易陷入局部最小值的缺陷[7-10],而時間序列分析[11-14]應用于隨機序列建模預測,具有靈活簡便的特點。

1 時間序列分析法建模

一個平穩、正態分布的隨機序列可以用自回歸滑動平均模型,即ARMA(p,q)模型表示為

(1)

如果模型中q=0,則模型退化為自回歸模型AR(p),即

xt=φ1xt-1+φ2xt-2+…+φpxt-p+εt

式中:φi(i=1…p)為自回歸系數。

時間序列分析方法建模要求隨機信號必須為平穩、正態、零均值序列。若原始信號不符合建模要求,則首先必須對信號進行預處理,當預處理后的殘差信號通過檢驗具備建模基礎后,根據自相關、偏自相關函數的統計特性,選取合適的模型階數并進行辨識,其一般過程包括:數據采集、數據統計分析與預處理、模型定階、模型參數辨識、模型檢驗等,如流程框圖1所示。

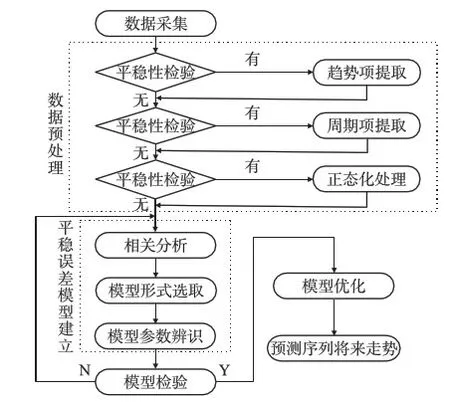
圖1 式時間序列分析建模流程圖

1.1 數據采集

光電穩定跟蹤平臺采用國產某型號低成本模擬MEMS陀螺,以256 Hz頻率采集常溫靜置下MEMS陀螺的X軸輸出作為原始漂移信號,采樣時間為10 min,選取當中的3 000個采樣點作為處理樣本,如圖2所示。

圖2 MEMS陀螺X軸原始漂移信號

1.2 數據預處理

受外部環境及內部因素的影響,MEMS陀螺原始漂移信號中包含常值分量、奇異值、趨勢項、周期項等誤差,難以保證其為平穩、正態、零均值序列。首先,采用萊特準則(3σ準則)剔除奇異點,去除其均值則為零均值序列;然后,通過一階或二階差分處理提取趨勢項,通過功率譜圖提取其周期項;最后,對預處理后的信號進行平穩性、正態性檢驗,以保證該殘差信號滿足建模所需要求。

對殘差信號的平穩性檢驗采取了游程檢驗法,假設n1是樣本一種觀測量的個數,n2是另一種觀測量的個數。如果序列平穩,那么有游程數r的均值和方差為

(2)

在顯著水平α=0.05下,游程個數檢驗變成U檢驗,r的范圍如下

(3)

如果U>1.96,則拒絕原假設,MEMS陀螺漂移序列為非平穩序列,進行差分處理。經檢驗,U=1.903 3<1.96,接受原假設,序列平穩。

預處理后的信號及正態檢驗如圖3和4所示。

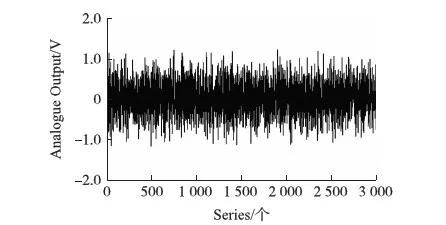
圖3 預處理后漂移信號

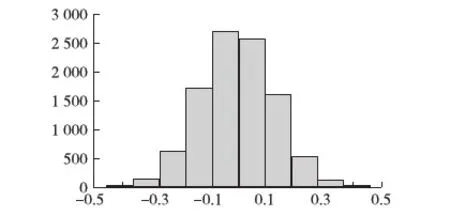
圖4 預處理后信號分布直方圖

1.3 模型定階、參數辨識及檢驗

MEMS 陀螺儀漂移模型的階次都比較低,一般不超過2到3階,根據自相關、偏自相關函數的統計特性,取漂移誤差模型階數為3,利用最小二乘法估計法得到對應的AR(3)和ARMA(2,1)模型系數分別如表1所示。

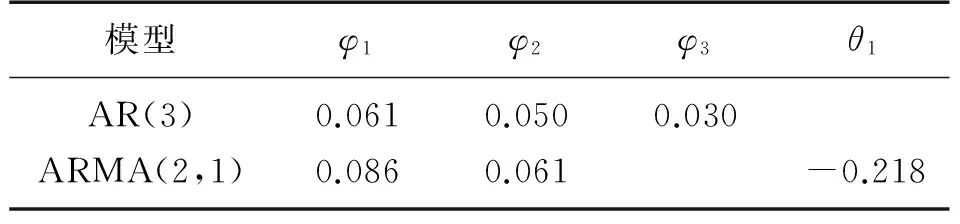
表1 誤差模型系數

根據最終預測誤差FPE(Final Prediction Error)準則,即

(4)

選取最終MEMS陀螺隨機漂移誤差模型為ARMA(2,1),預測估計結果如圖5所示。

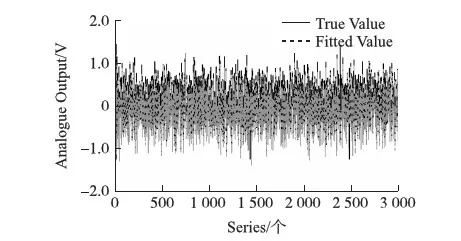
圖5 ARMA(2,1)模型預測結果

2 Kalman濾波

在上述MEMS陀螺漂隨機移誤差模型ARMA(2,1)基礎上,可采用Kalman濾波方法對MEMS陀螺漂移誤差進行補償。由漂移模型,系統的狀態方程和量測方程可描述為:

(5)

式中:φk,k-1為一步轉移矩陣;Wk-1為k-1時刻的系統噪聲;Гk-1為系統噪聲矩陣;Hk為k時刻的量測矩陣;Vk為k時刻的量測噪聲。參考文獻[12-13],濾波器參數設置如下:

設系統過程噪聲{Wk-1}和量測噪聲{Vk}的方差分別為Ok-1和Rk,取Ok-1為ARMA(2,1)模型殘差信號的方差,Rk為量測信號方差的十分之一,Pk|k-1為一步預測誤差的協方差矩陣,初值為單位矩陣;那么,Kalman濾波器的基本方程可寫為[15]

(6)

3 自適應Kalman濾波

在實際應用中很難得到系統精確的數學模型和噪聲的統計特性,致使濾波精度降低甚至產生濾波發散的現象。Sage和Husa提出的自適應Kalman濾波算法,其本質就是利用自身獲取的某些信息不斷估計和修正模型噪聲方差矩陣Q和量測噪聲R,不斷改進濾波器的設計,降低濾波誤差。在KF算法的基礎上引入遺忘因子d,可限制濾波器的記憶長度,使得新近數據充分參與到估計中發揮其作用,工程簡化算法如下

(7)

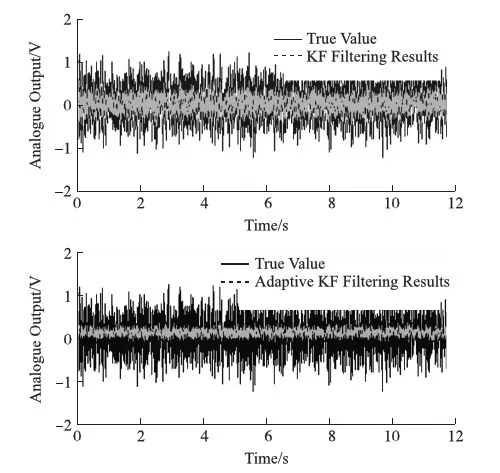
式中:dk為遺忘因子,0

4 驗證分析

利用數學工具MATLAB 7.0對MEMS陀螺X軸漂移數據進行了處理,噪聲為白噪聲序列,自適應Kalman算法的遺忘因子設值為0.98,處理結果如圖6和表2所示。

圖6 KF和自適應KF濾波結果

原始數據KF自適應KF均值0.03960.0033-0.0017方差0.17370.03870.0034

由圖6可以直觀看到,KF和自適應KF濾波后的漂移信號波動起伏明顯變小,由表2方差對比也可以看出濾波后的漂移信號方差比原始信號小了一個數量級,表明濾波后信號的分散程度顯著減小,而均值變化甚微,這主要是因為Kalman濾波屬于線性無偏最優估計。同時,較文獻[12-13]的KF算法,本文所采用的自適應KF算法具有更佳的效果。

5 結束語

本文對MEMS陀螺隨機漂移誤差特性進行了研究,在原始漂移信號統計分析及預處理的基礎上,建立了誤差ARMA(2,1)模型,并進行了Kalman濾波。濾波前后信號的方差對比表明有效降低了MEMS陀螺的漂移誤差,提高了實用性能。

[1] Meng T,Wang H,Li H,et al. Error Modeling and Filtering Method for MEMS Gyroscope[J]. Systems Engineering and Electronics,2009,8:30-38.

[2] Ningfang S,Jing C,Jing J. Wavelet Variance Analysis of Random Error Properties for Fiberoptic Gyroscope[J]. Infrared and Laser Engineering,2010,39(5):924-928.

[3] Wu W,Wang Y,Chen H,et al. Research on FOG Signal Process Based on wavelet transform[C]//Control,Mechatronics and Automation Technology:Proceedings of the International Conference on Control,Mechatronics and Automation Technology,2015,6(75):71-78.

[4] Song N,Chen J,Jin J. Wavelet Variance Analysis of Random Error Properties for Fiber Optic Gyroscope[J]. Infrared and Laser Engineering,2010,5:30-34.

[5] Li Z,Fan Q,Chang L,et al. Improved Wavelet Threshold Denoising Method for MEMS Gyroscope[C]//11th IEEE International Conference on Control and Automation(ICCA). IEEE,2014:530-534.

[6] 劉永. 小波分析在MEMS陀螺信號降噪中的應用研究[D]. 北京:國防科學技術大學,2011.

[7] Wu D,Fei J,Xue Y. Adaptive Neural Integral Sliding Mode Control Using Neural Compensator for MEMS Gyroscope[C]//2016 IEEE International Conference on Industrial Technology(ICIT). IEEE,2016:36-41.

[8] Chong S,Rui S,Jie L,et al. Temperature Drift Modeling of MEMS Gyroscope Based on Genetic-Elman Neural Network[J]. Mechanical Systems and Signal Processing,2016,72:897-905.

[9] Fei J,Wu D. Adaptive Control of MEMS Gyroscope Using Fully Tuned RBF Neural Network[J]. Neural Computing and Applications,2015:1-8.

[10] 王昊,王俊璞,田蔚風,等. 梯度RBF神經網絡在MEMS陀螺儀隨機漂移建模中的應用[J]. 中國慣性技術學報,2006,14(4):44-48.

[11] 趙靈. 基于MEMS陀螺儀的穩定平臺關鍵技術研究[D]. 南京:南京理工大學,2013.

[12] 吉訓生,王壽榮. MEMS 陀螺儀隨機漂移誤差研究[J]. 宇航學報,2009,27(4):640-642.

[13] 李杰,張文棟,劉俊. 基于時間序列分析的Kalman濾波方法在MEMS陀螺儀隨機漂移誤差補償中的應用研究[J]. 傳感技術學報,2006,19(05B):2215-2219.

[14] 代金華,張麗杰. 多準則MEMS陀螺隨機誤差在線建模與實時濾波[J]. 傳感技術學報,2016,29(1):75-79.

[15] 高鐘毓. 慣性導航系統技術[M]. 北京:清華大學出版社,2012:145-190.

Error Modeling and Filtering for Drift of MEMS Gyroscope*

LI Jie1,ZHENG Lungui1,2*,WANG Jianzhong1

(1.Educational Key Laboratory for Instrument Science and Dynamic Measurement,North University of China,Taiyuan 030051,China; 2.National Key Laboratory of Precision Measurement Technology and Instrument,Tsinghua University,Beijing 100084,China)

The control accuracy of the electro-optical stability tracking platform is directly affected by the drift error of MEMS gyroscope. The random drift error of MEMS gyroscope is slowly time-drifting,Weakly nonlinear and difficult to be accurately compensated. Aiming at the above characteristics,a model is built for the residual signal of MEMS gyro drift error based on the principle of time-series analysis. The Kalman filtering results show that the variance of the signal is improved by one to two magnitudes,which shows that the drift error is effectively suppressed and the accuracy of the MEMS gyroscope is improved.

MEMS gyroscope;random drift;time series analysis;Kalman filter

李 杰(1987-),男,河北人,博士研究生,測試計量技術與儀器專業,主要研究方向為慣性系統及測試,組合導航算法研究,583598264@qq.com;

鄭倫貴(1980-),男,四川人,講師,儀器科學與技術專業,主要研究方向為衛星姿態確定及控制,捷聯慣導和組合導航系統研究。

項目來源:清華大學精密測試技術及儀器國家重點實驗室開放基金項目(16106000005)

2016-10-10 修改日期:2017-01-16

TN914.42

A

1004-1699(2017)05-0731-04

C:7230

10.3969/j.issn.1004-1699.2017.05.016