α穩定分布噪聲下數字頻移鍵控信號的分數低階循環譜分析
劉高輝 張娟娟
(西安理工大學自動化與信息工程學院,西安 710048)
α穩定分布噪聲下數字頻移鍵控信號的分數低階循環譜分析
劉高輝 張娟娟
(西安理工大學自動化與信息工程學院,西安 710048)
針對α穩定分布噪聲環境下數字通信信號的二階與高階循環統計特征顯著退化問題,結合分數低階矩和共變理論對二進制頻移鍵控(Frequency Shift Keying, FSK)信號的分數低階循環譜公式進行了理論推導,并對2FSK信號在不同混合信噪比、分數階因子和特征指數條件下的分數低階循環譜進行了詳細的仿真分析. 理論和仿真結果表明:2FSK信號分數低階與二階的循環譜結構相同,其譜峰對應的循環頻率相同,譜峰的幅度值不同,取決于循環譜的階因子. 相對于在低混合信噪比下失效的二階循環譜,分數低階循環譜對α穩定分布噪聲具有更強的抗干擾性和適用性.
α穩定分布噪聲;2FSK信號;分數低階矩;共變理論;混合信噪比
DOI 10.13443/j.cjors.2017011001
引 言
在傳統的通信信號處理和雷達信號處理領域,信號的背景噪聲都被假定服從高斯分布,這種假設在大多數情況下是合理的. 近年來,隨著無線電技術的飛速發展,各種各樣的無線通信系統、雷達系統等信息化電子設備的數量與日俱增,導致無線系統接收信號的背景噪聲和干擾的強度日益增強,其統計特性在一些極端條件下具有非高斯性和非平穩性,如無線系統接收信號中出現的多用戶干擾、大氣低頻噪聲、自然界或人為產生的電磁脈沖噪聲通常表現出非高斯性,其時域波形具有顯著的尖峰特性,其幅度分布的概率密度函數具有較厚的拖尾特性. 因此,如果在無線通信系統中全部采用高斯分布模型來描述背景噪聲和干擾,將會由于模型與實際噪聲和干擾不匹配而導致所設計的信號處理算法性能嚴重退化. 利維(Levy)在1925年研究廣義中心極限定理時,首次提出α穩定分布的概念,它能夠很好地描述在時域具有顯著尖銳脈沖特性的非高斯噪聲. 因此α=0穩定分布的概念在數學界得到了廣泛應用,但是在信號處理領域并沒有得到發展和應用. 直到1993年經由C.L.Nikias等的系列論文[1-3],α穩定分布的概念和理論才開始在信號處理領域得到了重視,并且在近十年中得到了迅速發展和廣泛應用.
在無線通信中的各種通信信號由于載波調制、編碼、分數采樣等因素,通常為循環平穩信號,其二階和高階循環統計量是目前進行信號檢測和調制識別的有力工具[4-9]. 1987年,W.A.Gardner等人詳細介紹了調幅(Amplitude Modulation, AM)、頻率調制(Frequency Modulation, FM)、相位調制(Phase Modulation, PM)、二進制相移鍵控(Binary Phase Shift Keying, BPSK)、四進制相移鍵控(Quadrature Phase Shift Keying, QPSK)以及頻移鍵控(Frequency Shift Keying, FSK)等不同類型通信調制信號的頻譜相關函數[4-6]. 但是,在α=0穩定分布噪聲背景下,其二階和高階矩不存在. 因此,基于二階統計量有限假設的信號處理方法(如最小二乘估計,最大似然估計,循環譜相關方法等)將會顯著退化,甚至會導致錯誤的結果. 1993年,C.L.Nikias等在文獻[1-3]詳細分析了α穩定分布的基本特征以及α穩定噪聲下的分數低階矩理論.文獻[10-11]對高斯噪聲和脈沖噪聲環境下的QPSK信號的頻譜相關函數進行了分析,結果表明脈沖噪聲對信號的二階循環譜有很大影響. 文獻[12]對非高斯噪聲下的BPSK信號的循環譜進行了分析,得到了BPSK信號的分數低階循環譜結構.
頻移鍵控技術由于在抗干擾能力和對信道適應性等方面的突出優點,成為衰落信道下無線通信系統的一種主要調制技術. 迄今為止,對FSK信號分數低階循環譜的理論研究及仿真尚未見報道. 本文在前人的研究基礎上,結合分數低階矩理論以及循環平穩理論推導了二進制FSK信號的分數低階循環譜,并在α穩定分布噪聲下,對不同混合信噪比、不同特征指數α和不同階因子p的條件下對2FSK信號的分數低階循環譜進行了仿真分析.
1 基于共變的α穩定分布分數低階循環譜定義
1.1α穩定分布特征函數
由于α穩定分布的概率密度函數不存在統一、閉式的解析表示式,因此通常用特征函數對其進行描述. 標準參數系下α穩定分布的特征函數定義式為[8]
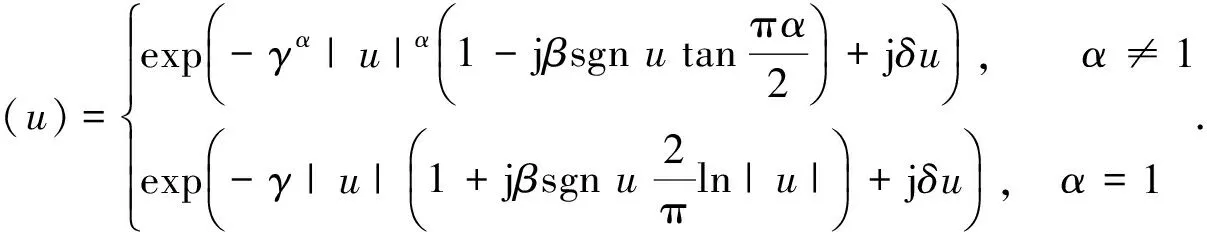
(1)

1.2 基于共變的分數低階循環譜定義
分數低階矩是一種分析處理非高斯信號的有力工具,若隨機信號的特征指數為α,則只有階數小于α的統計矩是有限的.對于α穩定分布噪聲下的信號x(t),分數低階矩定義式為
E[|X|p].
(2)
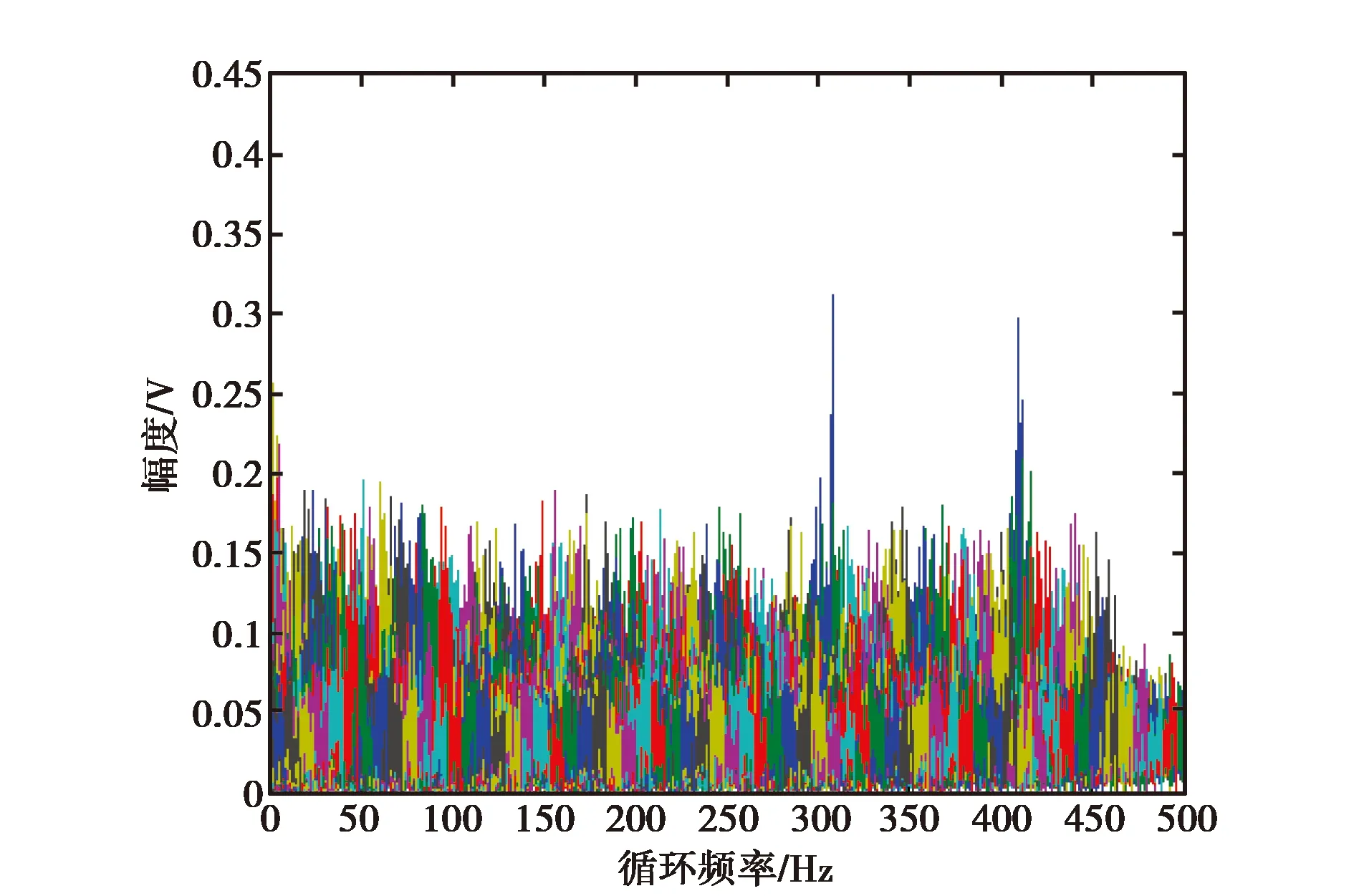
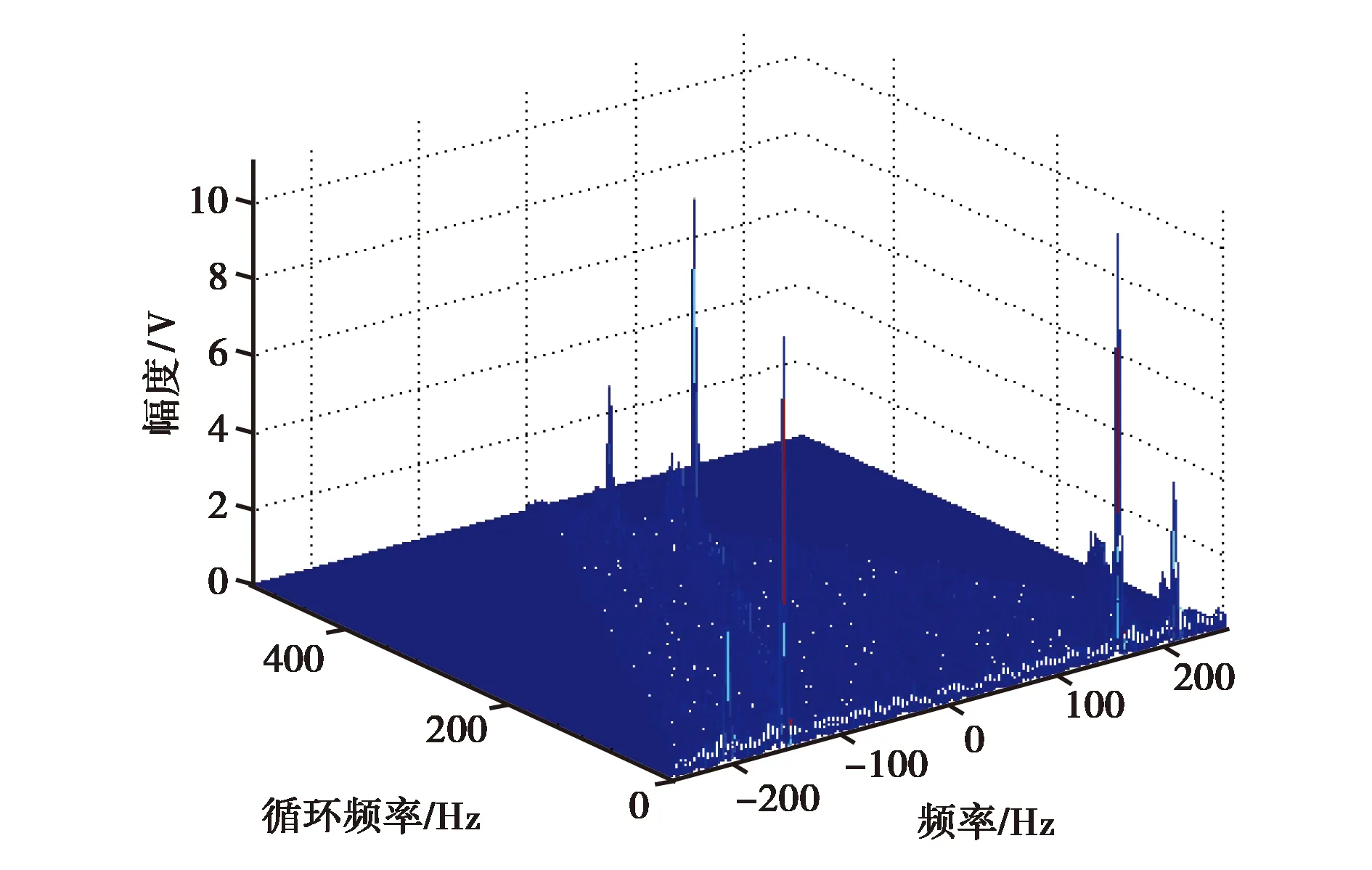
式中,p為分數階因子,其取值范圍為0 (3) 式中:τ為時間延遲;p為階因子,其取值范圍為[1,α),α為背景噪聲特征指數,取值范圍為[1,2]. 若COVx,p(t,τ)是關于t的周期函數,將其展開成傅里葉級數,傅里葉級數系數就是信號的分數低階循環自相關函數,其表示式為 (4) (5) 式中:f為常規頻率. 顯然,當階因子p=2時,分數低階循環譜密度函數即為二階循環譜密度函數. 假定2FSK信號x(t)表示為 (6) (7) 由復數過程的〈p〉符號運算定義式x〈p〉=|x|(p-1)·x*可知: (8) (9) 將式(8)和式(9)帶入式(7)中,則2FSK信號x(t)的p階共變可表示為 (10) 同理,由實數過程的〈p〉符號運算定義式 x〈p〉=|x|p·sgnx可知 (11) (12) 同理可得 (13) 將式(11)、式(12)和式(13)帶入式(10)中,則式(10)可化簡為 (14) 式(14)第一項中求期望部分可以表示為 (15) 因為隨機序列an為廣義平穩序列,其自相關函數可以表示為Ra(m)=E[anan+m],故式(15)可表示為: (16) 式(16)中,m=q-n. 同理,式(14)中第二項求期望部分可以表示為 (17) 同理,可得到式(14)中第三項和第四項期望的結果. COVx,p(t,τ)=kp1· (18) (19) (20) 式(20)中:β=m/Ts,m為整數. 則式(18)可表示為 Rxx(τ)·[ej2πf2τ+e-j2πf2τ+ej4πf2t+e-j4πf2t]. (21) 對式(21)求傅里葉系數得 (22) 由于傅里葉級數的系數即為循環自相關函數,因此,結合式(20)整理式(22)即可得2FSK信號的分數低階循環自相關函數的表達式為 (23) 對式(23)再求一次傅里葉變換,即可得到2FSK信號的分數低階循環譜密度函數. 通過上述2FSK信號分數低階循環譜的理論推導可知,當循環頻率ε=β+k時,2FSK信號存在循環譜線,其中β=m/Ts(m為整數),k=0、±2f1和±2f2. 顯然循環譜譜峰對應的循環頻率與2FSK信號的碼元速率和載波頻率有關. 本文采用離散頻域平滑估計算法,對在不同混合信噪比(Mixed Signal-to-Noise Ratio, MSNR)、不同特征指數α以及不同分數階因子p條件下2FSK信號的分數低階循環譜進行了計算仿真與分析. 3.1 不同MSNR下分數階循環譜曲線 噪聲和信號參數分別為:特征指數α=1.8,對稱參數β=0,分散系數γ=1和位置參數δ=0;2FSK信號的載頻f1=154 Hz,載頻f2=205 Hz,符號間隔Ts=0.5 s. 仿真條件為:分數低階因子p=1.5,數據長度N=2 560,頻域平滑點數為20. 對2FSK信號在 MSNR為[8, 4,-2] dB時分數低階循環譜截面如圖1、圖2和圖3所示. 為了對比分析,本文還給出了在相同信號參數和仿真條件下,MSNR分別為8 dB和4 dB時2FSK信號的二階循環譜曲線,如圖4和圖5所示. 圖1 MSNR為8 dB時2FSK信號的p=1.5階循環譜截面 圖2 MSNR為4 dB時2FSK信號的p=1.5階循環譜截面 圖3 MSNR為-2 dB時2FSK信號的p=1.5階循環譜截面 圖4 MSNR為8 dB時2FSK信號的二階循環譜 圖5 MSNR為4 dB時2FSK信號的二階循環譜 從圖1、圖2和圖3的仿真結果可以明顯地看出,在α穩定分布噪聲下,采用分數低階循環譜的算法,當混合信噪比大于-2 dB時2FSK信號的循環譜中譜峰的位置都能夠比較清楚地觀察到. 而從圖4和圖5的仿真結果可以明顯地看出,在相同的條件下,2FSK信號的二階循環譜線的譜峰在混合信噪比為8 dB時就已完全看不清.這說明傳統二階循環譜算法在較高信噪比時已經失效,檢測不出來信號所對應的譜線.而基于分數低階循環統計量的方法在較低信噪比時仍然能夠明顯地檢測出2FSK信號的譜線. 基于分數低階循環譜的算法在α穩定分布噪聲背景下比二階循環譜算法更有效. 3.2 不同特征指數α下分數階循環譜曲線 噪聲和信號參數分別為:特征指數α=1.8,對稱參數β=0,分散系數γ=1和位置參數δ=0;2FSK信號的載頻f1=154 Hz,載頻f2=205 Hz,符號間隔Ts=0.5 s. 圖6 α=1.6時2FSK信號p=1.5階循環譜 圖7 α=1.4時2FSK信號p=1.5階循環譜 圖8 α=1.2時2FSK信號p=1.5階循環譜 圖9 α=0.8時2FSK信號p=1.5階循環譜 仿真條件為:分數低階因子p=1.5,數據長度N=2 560,頻域平滑點數為20. 在特征指數α分別為[1.6,1.4,1.2,0.8]時,2FSK信號分數低階循環譜曲線如圖6、圖7、圖8和圖9所示. 從圖6、圖7、圖8和圖9的仿真結果可以看出:隨著特征指數α減小,其循環譜線變得越來越不明顯,當α<1時,信號的譜線完全淹沒在噪聲當中.這是因為α穩定分布噪聲的特征指數α越小,脈沖特性越強,對譜線的影響就越大,而且本文基于共變的算法也只適用于α>1的情況.仿真結果與理論分析相一致. 3.3 不同分數低階因子p下循環譜曲線 噪聲和信號參數分別為:特征指數α=1.8,對稱參數β=0,分散系數γ=1和位置參數δ=0;MSNR為4 dB,信號載頻f1=154 Hz和f2=205 Hz,符號間隔Ts=0.5 s. 仿真條件為:數據長度N=2 560,頻域平滑點數為20. 在分數階因子p為1.8和1.5時,2FSK信號分數低階循環譜曲線如圖10和圖11所示. 從圖10和圖11的仿真結果可以看出:分數階因子p只對循環譜的峰值有所影響,并不會影響循環譜峰的位置,而且p值越大,循環譜峰值也越大. 圖10 α=1.8時2FSK信號p=1.8階循環譜 圖11 α=1.8時2FSK信號p=1.5階循環譜 本文結合分數低階矩和共變理論對α穩定分布噪聲下2FSK信號的分數低階循環譜進行了理論推導,并對2FSK信號在不同混合信噪比、分數階因子和特征指數條件下的分數低階循環譜進行了詳細的仿真分析. 從仿真結果中可以得到以下結論:1)2FSK信號的分數低階循環譜和二階循環譜具有相同的譜結構,二者的循環頻率相同,只是譜線峰值有所不同,其值取決于分數階因子p;2)在α穩定分布噪聲下,MSNR為8 dB時2FSK信號的二階循環譜線已經完全淹沒在噪聲里面,而在相同條件下基于分數低階循環統計量的方法在MSNR為-2 dB時仍然能夠明顯地檢測出2FSK信號的循環譜線;3)隨著特征指數α的減小,信號的分數階循環譜線變得越來越不明顯,當α<1時,循環譜線完全被淹沒;4)分數階因子p對循環譜峰位置沒有影響,只是對譜峰的數值有所影響. 這些仿真結果表明α穩定分布噪聲下2FSK信號的分數低階循環譜的結構、循環頻率、循環譜峰值等可以作為MFSK信號的識別、參數估計和檢測的特征量,相對于二階循環譜,分數低階循環譜特征對α穩定分布噪聲具有更強的抗干擾性和適用性. [1] SHAO M, NIKIAS C L. Signal processing with fractional lower order moments: stable processes and their applications[J]. Proceedings of the IEEE, 1993, 81(7): 986-1010. [2] SHAO M, NIKIAS C L. Signal processing with alpha-stable distribution and applications[M]. New York: John Wiley &Sons Inc, 1995. [3] MA X Y, NIKIAS C L. Joint estimation of time delay and frequency delay in impulse noise using fractional lower order statistics[J]. IEEE transactions on signal processing, 1996,44(11): 2669-2687. [4] GARDNER W A. Measurement of spectral correlation[J]. IEEE transactions on acoustics, speech, and signal processing, 1986, 34(5): 1111-1123. [5] GARDNER W A, BROWN W A. Spectral correlation of modulation signals: part I-analog modulation[J]. IEEE transactions on communication, 1987, 35(6): 584-594. [6] GARDNER W A, BROWN W A. Spectral correlation of modulation signals: part II-digital modulation[J]. IEEE transactions on communication, 1987, 35(6): 595-601. [7] 黃知濤. 循環平穩信號處理及其應用研究[D]. 長沙: 國防科技大學, 2003. HUANG Z T. Researches on cyclostationary signal processing and applications[D]. Changsha: National University of Defense Technology, 2003. (in Chinese) [8] 張賢達, 保錚. 非平穩信號分析與處理[M].北京: 國防工業出版社, 1998. [9] 邱天爽, 張旭秀, 李小兵, 等. 統計信號處理——非高斯信號處理及其應用[M]. 北京: 電子工業出版社, 2004. [10]劉洋.穩定分布噪聲下循環平穩信號時延與多普勒頻移估計方法研究[D]. 大連: 大連理工大學, 2012. LIU Y. A study of estimation of time and frequency difference of arrival for cyclostationary signals in stable impulse noise[D]. Dalian: Dalian University of Technology, 2012. (in Chinese) [11]孫永梅, 邱天爽, 李暉, 等. α穩定分布過程的譜分析方法[J]. 大連交通大學學報, 2010, 31(4): 9-12. SUN Y M, QIU T S, LI H,et al. Study of spectrum analysis method of α stable distribution process[J]. Journal of Dalian Jiaotong University, 2010, 31(4): 9-12. (in Chinese) [12]何繼愛, 裴承全, 蒲陽陽.非高斯模型下BPSK的循環譜分析[J]. 蘭州大學學報(自然科學版), 2012, 48(3): 133-138. HE J A, PEI C Q, PU Y Y. Cyclic spectrum analysis of BPSK under a non-Gaussian model[J]. Journal of Lanzhou University(natural sciences), 2012, 48(3): 133-138. (in Chinese) 張娟娟 (1992-),女,甘肅人,西安理工大學自動化與信息工程學院碩士研究生,研究方向為通信信號處理. Fractional lower order cyclic spectrum analysis of digital frequency shift keying signals under the alpha stable distribution noise LIU Gaohui ZHANG Juanjuan (SchoolofAutomationandInformationEngineering,Xi’anUniversityofTechnology,Xi’an710048,China) Aiming at the significant degradation of the statistical characteristics of the second and higher order cycle of the digital communication signal in the alpha stable distributed noise environment, the fractional lower-order cyclic spectrum formula of the frequency shift keying(FSK) signal is deduced with the fractional lower-order moments and the covariant theory. Then, the low-order cyclic spectrum characteristics of 2FSK signal under different mixed signal-to-noise ratios, fractional factors and characteristic exponents were analyzed in detail. The theory and simulation results show that the low-order and second-order cyclic spectrum structures of the 2FSK signal are the same, and the peak frequencies of the 2FSK signal are the same, but the amplitude of the spectrum is different that depending on the order factor of the cyclic spectrum. Fractional lower-order cyclic spectrum has stronger anti-interference and applicability to alpha stable distributed noise. alpha stable distribution noise; 2FSK signal; fractional lower order moment; covariant theory; mixed signal-to-noise ratio 2017-01-10 國家自然科學基金(No.61671375) 10.13443/j.cjors.2017011001 TN911.7 A 1005-0388(2017)01-0065-08 劉高輝 (1968-),男,陜西人,西安理工大學自動化與信息工程學院副教授,博士,研究方向為通信信號處理和雷達信號處理. 聯系人: 劉高輝 E-mail: liugh68@xaut.edu.cn 劉高輝, 張娟娟.α穩定分布噪聲下數字頻移鍵控信號的分數低階循環譜分析[J]. 電波科學學報,2017,32(1):65-72. LIU G H, ZHANG J J. Fractional lower order cyclic spectrum analysis of digital frequency shift keying signals under the Alpha stable distribution noise[J]. Chinese journal of radio science,2017,32(1):65-72. (in Chinese). DOI: 10.13443/j.cjors.2017011001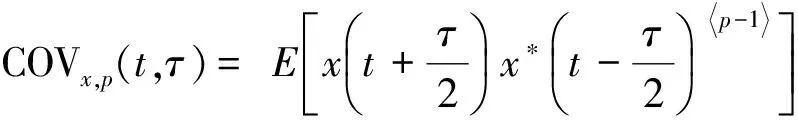
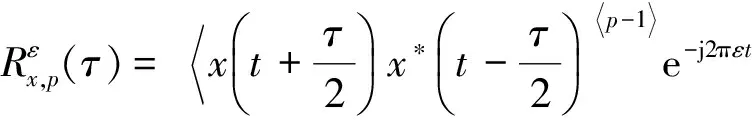

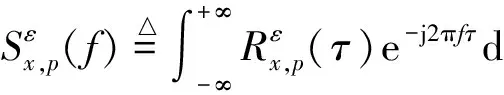
2 2FSK信號的分數低階循環譜理論推導


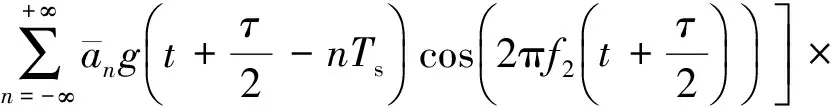


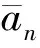




3 2FSK信號分數低階循環譜仿真分析







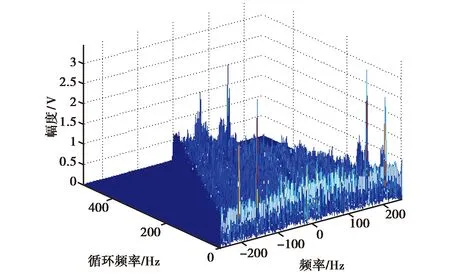


4 結 論



