約束阻尼結(jié)構(gòu)的改進準(zhǔn)則法拓撲減振動力學(xué)優(yōu)化

賀紅林， 袁維東， 夏自強， 劉堯弟

(南昌航空大學(xué) 航空制造工程學(xué)院，南昌 330063)

約束阻尼結(jié)構(gòu)的改進準(zhǔn)則法拓撲減振動力學(xué)優(yōu)化

賀紅林， 袁維東， 夏自強， 劉堯弟

(南昌航空大學(xué) 航空制造工程學(xué)院，南昌 330063)

旨在為減振設(shè)計提供理論基礎(chǔ)，研究約束阻尼結(jié)構(gòu)拓撲動力學(xué)優(yōu)化。以阻尼材料用量、振動特征方程、模態(tài)頻率為約束，以多模態(tài)損耗因子倒數(shù)的加權(quán)和最小為目標(biāo)，建立了約束阻尼結(jié)構(gòu)拓撲優(yōu)化模型，引入MAC因子控制結(jié)構(gòu)的振型躍階。在引入質(zhì)量陣懲罰因子基礎(chǔ)上推導(dǎo)出優(yōu)化目標(biāo)靈敏度。考慮到優(yōu)化目標(biāo)函數(shù)的非凸性，采用常規(guī)準(zhǔn)則法(OC)尋優(yōu)可能會使拓撲變量出現(xiàn)負值或陷入局部優(yōu)化，故引入數(shù)學(xué)規(guī)劃移動漸近技術(shù)對OC法進行改進，從而將全體拓撲變量納入改進算法的優(yōu)化迭代全過程。編程實現(xiàn)了約束阻尼板改進OC法拓撲動力學(xué)優(yōu)化并對改進法性能進行了仿真。結(jié)果顯示,改進算法可得到更合理的約束阻尼層構(gòu)形，可使結(jié)構(gòu)取得更佳減振效果。研究表明,改進算法迭代穩(wěn)定性更好、尋優(yōu)效率更高、更具全域最優(yōu)性。

約束阻尼板；多模態(tài)損耗因子；改進優(yōu)化準(zhǔn)則法；減振特性；動力學(xué)拓撲優(yōu)化

隨著航空航天和先進制造等現(xiàn)代科技發(fā)展，機械日趨高速和大動力化，使結(jié)構(gòu)所受激擾越來越多、運行環(huán)境愈發(fā)復(fù)雜且不斷惡化，導(dǎo)致結(jié)構(gòu)振動問題日趨突出。振動不僅帶來噪聲、結(jié)構(gòu)失效、機械工作精度下降等問題，嚴(yán)重時還可能導(dǎo)致振動疲勞而引發(fā)事故，因此如何有效地控制振動已成為機械設(shè)計的重要課題。采用隔振、吸振、減振等可有效控制機械結(jié)構(gòu)振動，其中，在結(jié)構(gòu)表面附加黏彈性阻尼材料作為一種被動減振技術(shù)，已被驗證為一種實用、有效振動控制措施，近年來得到了廣泛應(yīng)用[1]。實踐表明，黏彈阻尼材料能在相當(dāng)寬的頻帶內(nèi)對結(jié)構(gòu)振動起到較大抑制作用。在結(jié)構(gòu)上附加黏彈阻尼的方式主要有兩種,即自由阻尼結(jié)構(gòu)和約束阻尼結(jié)構(gòu)[2]。后者因可產(chǎn)生強烈的振動能耗散效應(yīng)，且能有效地控制多峰諧振，故工程應(yīng)用更為廣泛。然而，若在結(jié)構(gòu)全域均附加阻尼材料必導(dǎo)致結(jié)構(gòu)重量巨增，有悖于結(jié)構(gòu)輕量化設(shè)計思想。因此如何在嚴(yán)格控制阻尼材料用量條件下，使結(jié)構(gòu)獲得最佳減振效果，成為阻尼結(jié)構(gòu)設(shè)計的共性問題。

要改善結(jié)構(gòu)動態(tài)性能并降低其動響應(yīng)，可借助拓撲優(yōu)化手段[3]。為此，針對阻尼結(jié)構(gòu)優(yōu)化，楊德慶[4]提出阻尼胞抑振單元和拓撲優(yōu)化敏度并據(jù)此建立了阻尼材料優(yōu)化配置準(zhǔn)則；韋勇等[5]提出了快速拓撲優(yōu)化法；李攀等[6]基于SIMP插值研究了約束阻尼結(jié)構(gòu)拓撲優(yōu)化。考慮到優(yōu)化準(zhǔn)則法(Optimal Criterion，OC)是作為靜力學(xué)拓撲優(yōu)化的主要方法之一[7]，為此，郭中澤等[8]將其引入阻尼結(jié)構(gòu)拓撲優(yōu)化并指出該方法同樣適于結(jié)構(gòu)動力學(xué)優(yōu)化及輕量化設(shè)計；鄭玲等[9]分別研究了約束阻尼板和自由阻尼板變密度優(yōu)化并應(yīng)用一般優(yōu)化準(zhǔn)則法實現(xiàn)了阻尼板求解，并在準(zhǔn)則法的靈敏度項處理中僅采用大于0的靈敏值，作為對靜力優(yōu)化OC法的改進。鑒于約束阻尼結(jié)構(gòu)耗能主要源于其黏彈阻尼層剪切變形，模態(tài)損耗因子則是衡量能耗大小的主指標(biāo)，為此Johnson等[10]在對阻尼結(jié)構(gòu)復(fù)特征解簡化為實特征解的基礎(chǔ)上，提出基于模態(tài)應(yīng)變能(Modal Strain Energy，MSE)的損耗因子計算方法。

由于一般優(yōu)化準(zhǔn)則法數(shù)學(xué)意義明晰，用于結(jié)構(gòu)靜力學(xué)拓撲優(yōu)化迭代時能確保拓撲變量的正值性，故在靜力學(xué)設(shè)計中得到了很好的應(yīng)用。但在將其用于拓撲動力學(xué)優(yōu)化時，因優(yōu)化目標(biāo)函數(shù)可能存在非凸特性，故優(yōu)化迭代中不一定能保證設(shè)計變量的非負性，從而可能導(dǎo)致迭代過程不收斂或局域收斂[11]。為滿足動力學(xué)設(shè)計要求并發(fā)揮OC法優(yōu)勢，本文對OC法進行改進。改進法保留了OC法的優(yōu)點并避免了設(shè)計變量迭代發(fā)散等問題，同時，為使阻尼結(jié)構(gòu)在較寬頻域具有良好減振特性，文中著重探索了多模態(tài)減振優(yōu)化問題。

1 有限元法動力學(xué)求解

阻尼結(jié)構(gòu)動力學(xué)問題求解通常采用有限元法，具體實施可采用復(fù)特征值法、模態(tài)應(yīng)變能法(MSE)、直接頻率響應(yīng)法，其中MSE法在計算中忽略振動模態(tài)的虛部，可避免復(fù)雜的復(fù)特征值與特征向量計算，特別是當(dāng)結(jié)構(gòu)的特性以彈性為主導(dǎo)時，采用此法可獲得較高的動力學(xué)計算精度。考慮到本文將基于模態(tài)損耗因子推進阻尼結(jié)構(gòu)拓撲動力學(xué)優(yōu)化，優(yōu)化迭代中涉及大量的動力學(xué)參數(shù)計算，故為提高優(yōu)化效率而采用MSE計算阻尼板模態(tài)損耗因子。對于彈性主導(dǎo)的約束阻尼板，若不考慮能量損失，則根據(jù)Hamilton原理可構(gòu)建立阻尼板振動之廣義特征方程

(K-ω2M)φ=0

(1)

對式(1)求解，即可得到阻尼板模態(tài)頻率ωj及振型φj。

約束阻尼板主要通過黏彈材料實現(xiàn)耗散效應(yīng)，板內(nèi)金屬層的耗能能力與黏彈層相比要低幾個數(shù)量級，通常可忽略。黏彈性動力學(xué)理論表明，可用以描述黏彈層力學(xué)本構(gòu)的數(shù)學(xué)模型有多種，但較為實用是常復(fù)數(shù)模量模型[12]。若從該模型出發(fā)，則不難推導(dǎo)出阻尼板的i階模態(tài)損耗因子的計算式,即

ηi=ηvEv,i/ET,i

ET,i=Ev,i+Ebc,i,Ebc,i=Eb,i+Ec,i

(2)

式中:ηv為黏彈層材料的損耗因子；Eb,i、Ev,i、Ec,i分別為基層、阻尼層、約束層的i階模態(tài)應(yīng)變能；ET,i為阻尼板的i階模態(tài)總應(yīng)變能。

對于以彈性為主導(dǎo)的約束阻尼結(jié)構(gòu)，其模態(tài)損耗因子與模態(tài)阻尼比間大致存在關(guān)系：ηi≈2ξi。據(jù)此，可推得阻尼板第i階模態(tài)的振動平衡方程

(3)

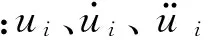
2 拓撲減振動力學(xué)優(yōu)化建模

2.1 拓撲優(yōu)化數(shù)學(xué)模型

如同結(jié)構(gòu)尺寸優(yōu)化一樣，約束阻尼板拓撲動力學(xué)優(yōu)化同樣需以一定的優(yōu)化目標(biāo)指明迭代方向，并評價優(yōu)化結(jié)果。針對阻尼結(jié)構(gòu)減振設(shè)計，該目標(biāo)既可設(shè)定為結(jié)構(gòu)的振動位移響應(yīng)或若干特征點的振幅，也可以是模態(tài)阻尼比或模態(tài)損耗因子，還可以是結(jié)構(gòu)的動撓度、模態(tài)頻率等。考慮到模態(tài)損耗因子能綜合地反映結(jié)構(gòu)在一定頻段內(nèi)振動時的總體耗能和減振效果，故選定模態(tài)損耗因子為優(yōu)化目標(biāo)。這樣，阻尼結(jié)構(gòu)拓撲動力學(xué)優(yōu)化便是通過合理配置約束阻尼層的材料布局，使結(jié)構(gòu)的特定階次模態(tài)損耗因子最大。然而，在規(guī)范的優(yōu)化數(shù)學(xué)模型中，目標(biāo)函數(shù)須以最小化形式出現(xiàn)，以便借助現(xiàn)存的一些成熟優(yōu)化迭代技術(shù)推進優(yōu)化。在優(yōu)化建模時，有必要先求取模態(tài)損耗因子的倒數(shù)，再以該倒數(shù)作為模型中的目標(biāo)函數(shù)。在阻尼減振設(shè)計時，通常對阻尼材料用量提出嚴(yán)格限制以保證結(jié)構(gòu)輕量化，并且為保證結(jié)構(gòu)的預(yù)期功能，還要求黏彈層的鋪設(shè)不能造成結(jié)構(gòu)動態(tài)特性如頻率、模態(tài)、振型等發(fā)生太大改變。考慮上述因素，為阻尼減振結(jié)構(gòu)建立拓撲動力學(xué)優(yōu)化數(shù)學(xué)模型為

(4)

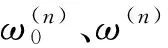
結(jié)構(gòu)振動研究表明，彈性結(jié)構(gòu)中階次較低的模態(tài)通常是對振動位移響應(yīng)貢獻較大的主導(dǎo)模態(tài)。在減振設(shè)計時，關(guān)鍵是要抑制或降低主導(dǎo)模態(tài)振動響應(yīng)，即對主導(dǎo)模態(tài)實施控振措施。事實上，即便是各主導(dǎo)模態(tài)，在結(jié)構(gòu)處于不同激擾條件時如當(dāng)結(jié)構(gòu)激振頻率不同時，其振動貢獻也會發(fā)生一定改變。這意味著需在目標(biāo)函數(shù)中引入不同的權(quán)值?i以強化對主導(dǎo)模態(tài)的減振效應(yīng)，且最好依據(jù)模態(tài)參與因子取定?i。當(dāng)然，若結(jié)構(gòu)僅存在單頻激勵且激振頻率、激勵方向與某階模態(tài)相契合，則只需控制該模態(tài)振動即可。事實上，單一模態(tài)優(yōu)化只作為多模態(tài)復(fù)合優(yōu)化的特例。

2.2 優(yōu)化目標(biāo)靈敏度計算

優(yōu)化目標(biāo)對于優(yōu)化變量的靈敏度指設(shè)計變量發(fā)生單位變化時所引起優(yōu)化目標(biāo)值的改變量，其數(shù)學(xué)含義即是目標(biāo)函數(shù)對于拓撲變量的導(dǎo)數(shù)和梯度。靈敏度計算為阻尼板減振優(yōu)化提供迭代方向。式(4)的目標(biāo)函數(shù)對于設(shè)計變量的靈敏度可寫成

?i[?(1/ηi)/?xnm]

(5)

?(1/ηi)/?xnm=[Ev,i(?Ebc,i/?xnm)-

可看出只要求得能量的相關(guān)參數(shù)便可求解目標(biāo)函數(shù)值。

采用OC法求解阻尼板拓撲優(yōu)化問題時，須設(shè)定黏彈層單元物理參數(shù)、力學(xué)特性參數(shù)如密度和彈性模量等與拓撲變量間的關(guān)系，考慮到阻尼結(jié)構(gòu)減振優(yōu)化不涉及基層單元改變，故可設(shè)基層單元特性恒定，而黏彈層和約束層單元均采用固體各向同性材料懲罰(Solid Isotropic Microstructures with Penalization，SIMP)，即令

(6)

式中:Eo、ρo為彈性材料在優(yōu)化迭代的基本彈性模量密度;p、q為適當(dāng)取定的正值懲罰因子式。將式(6)代入黏彈單元、約束層單元剛度陣及質(zhì)量陣，且令剛度陣和質(zhì)量陣對拓撲變量求導(dǎo)，則可推導(dǎo)出

(7)

式中:SEi、KEi分別為單元的i階模態(tài)應(yīng)變能和模態(tài)動能；cm、vm為約束單元、阻尼單元標(biāo)識符。

3 優(yōu)化模型改進OC法求解

已有研究表明，當(dāng)采用優(yōu)化準(zhǔn)則法實現(xiàn)工程結(jié)構(gòu)靜力學(xué)拓撲優(yōu)化求解時，通常能較好地迭代出結(jié)構(gòu)的拓撲全域最優(yōu)解。但在采用該方法推進動力學(xué)拓撲優(yōu)化時，因所針對的目標(biāo)函數(shù)不一定具有嚴(yán)格的數(shù)學(xué)凸性，故在優(yōu)化迭代中計算出的目標(biāo)函數(shù)靈敏度不僅有正值出現(xiàn)也可能產(chǎn)生負值。拓撲靜力學(xué)OC法優(yōu)化中，只會產(chǎn)生正值靈敏度，這是兩類優(yōu)化問題在迭代中的最大不同之處，它表明在進行拓撲動力學(xué)優(yōu)化時，若簡單地采用常規(guī)OC法，則難免出現(xiàn)設(shè)計變量被迭代為負值的不合理情況。當(dāng)然，在動力學(xué)優(yōu)化程序中通過人為設(shè)定拓撲變量取值范圍，或忽略負值靈敏度，可避免變量負值設(shè)計變量并為后續(xù)迭代做好準(zhǔn)備，但這樣做勢必帶來拓撲變量值跳躍及其迭代不連續(xù)狀況，從而導(dǎo)致最終迭代出的解并非全域最優(yōu)。正因如此，本文在對常規(guī)的拓撲優(yōu)化OC法進行改進的基礎(chǔ)上，提出了阻尼板拓撲動力學(xué)減振優(yōu)化OC法。

3.1 OC法的數(shù)學(xué)規(guī)劃意義改進

在求解優(yōu)化目標(biāo)函數(shù)以及使其具有凸性的算法中，數(shù)學(xué)規(guī)劃法的序列凸規(guī)劃方法，是以泰勒展開式思想對目標(biāo)函數(shù)和約束函數(shù)進行處理，下面基于此思想，對常規(guī)拓撲動力學(xué)OC法進行改進。根據(jù)優(yōu)化理論，基于式(4)構(gòu)造常規(guī)拉格朗日函數(shù)

(8)

式中，λ、α-nm、α+nm均為拉格朗日乘子。對于滿足Karush-Kuhn-Tucke條件的優(yōu)化問題，必存在如下關(guān)系

(9)

引入移動參數(shù)μ，且令λ*=λ+μ，Γ*=Γ-μV，并將它們代入式(9)，則易得

(10)

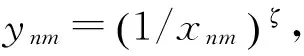
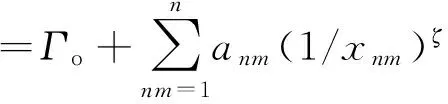
(11)

式中，Γo為一常數(shù)。式(11)對拓撲變量求導(dǎo)，則有

?Γ*/?xnm=?(Γ-μV)/?xnm=?[anm(xnm)-ζ]/?xnm

?Γ*/?ynm=anm

(12)

將式(12)進行化簡并經(jīng)整理后，可得

anm=-[?Γ/?xnm-μ(?V/?xnm)](xnm)ζ+1/ζ

μ≥(?Γ/?xnm)/(?V/?xnm)

(13)

式(13)表明，anm≥0，且近似函數(shù)Γ*具有嚴(yán)格凸性。

3.2 改進OC法的優(yōu)化迭代格式

為便于行文，在此先令bnm=?V/?xnm并將其代入式(8)，這樣便將拉格朗日優(yōu)化函數(shù)改寫成

(14)

式(14)中，

式中，A、B、C分別為拓撲變量中間值、最小值和最大值之集合。式(14)的解可基于式(9)、式(10)并通過求解類似于下述問題而得到，即求解

min:lnm，xmin≤xnm≤xmax

(15)

為此，令?lnm/xnm=0，并使其滿足Karush-Kuhn-Tucker條件，這樣便得到

xnm=(ζanm/λbnm)1/1+ζ

(16)

當(dāng)采用不動點迭代法時，可將設(shè)計變量迭代式寫成

(17)

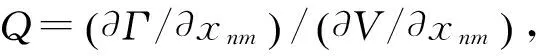
(18)

式中，

式中，ζ為設(shè)計變量更新后的極限值。

阻尼板拓撲動力學(xué)優(yōu)化從本質(zhì)上講就是在滿足各種約束的條件下，通過不斷推進迭代尋求最優(yōu)拓撲解。如果在迭代中拓撲變量值變化太大，使得單元的剛度和密度之比不合理，必引致結(jié)構(gòu)振型大幅改變。為避免振型的躍階，在優(yōu)化模型中引入振型控制因子約束，以控制振型變化，即令

(19)

式中，χ為<1的正值系數(shù)，可取0.9。尋優(yōu)迭代推進時，程序?qū)AC值進行跟蹤，并適當(dāng)調(diào)整迭代方向盡量使MAC接近于1，以保證振型的穩(wěn)定性。

3.3 改進OC優(yōu)化算法實現(xiàn)

為了實現(xiàn)基于式(18)迭代格的改進OC法拓撲動力學(xué)優(yōu)化，本文發(fā)揮MATLAB的數(shù)值計算優(yōu)勢以及ANSYS有限元軟件的動力學(xué)建模及求解優(yōu)勢，綜合利用MATLAB編程語言及ANSYS 提供的ADPL二次開發(fā)語言，編制出約束阻尼板拓撲優(yōu)化計算程序。該程序?qū)ATLAB當(dāng)作優(yōu)化迭代外殼，以ANSYS作為阻尼板動力學(xué)特性有限元建模與求解內(nèi)核，利用前者完成設(shè)計變量的靈敏度計算、尋優(yōu)迭代、MAC (Modal Assurance Criterion)值計算等優(yōu)化內(nèi)容，利用后者求解阻尼板的振動模態(tài)、模態(tài)頻率、質(zhì)量陣、剛度陣、阻尼陣等。兩者之間通過共享內(nèi)存的方式實現(xiàn)數(shù)據(jù)交換并基于MATLAB為ANSYS提供的軟件接口，實現(xiàn)二者銜接。圖1給出阻尼板改進OC法尋優(yōu)迭代的實現(xiàn)流程。

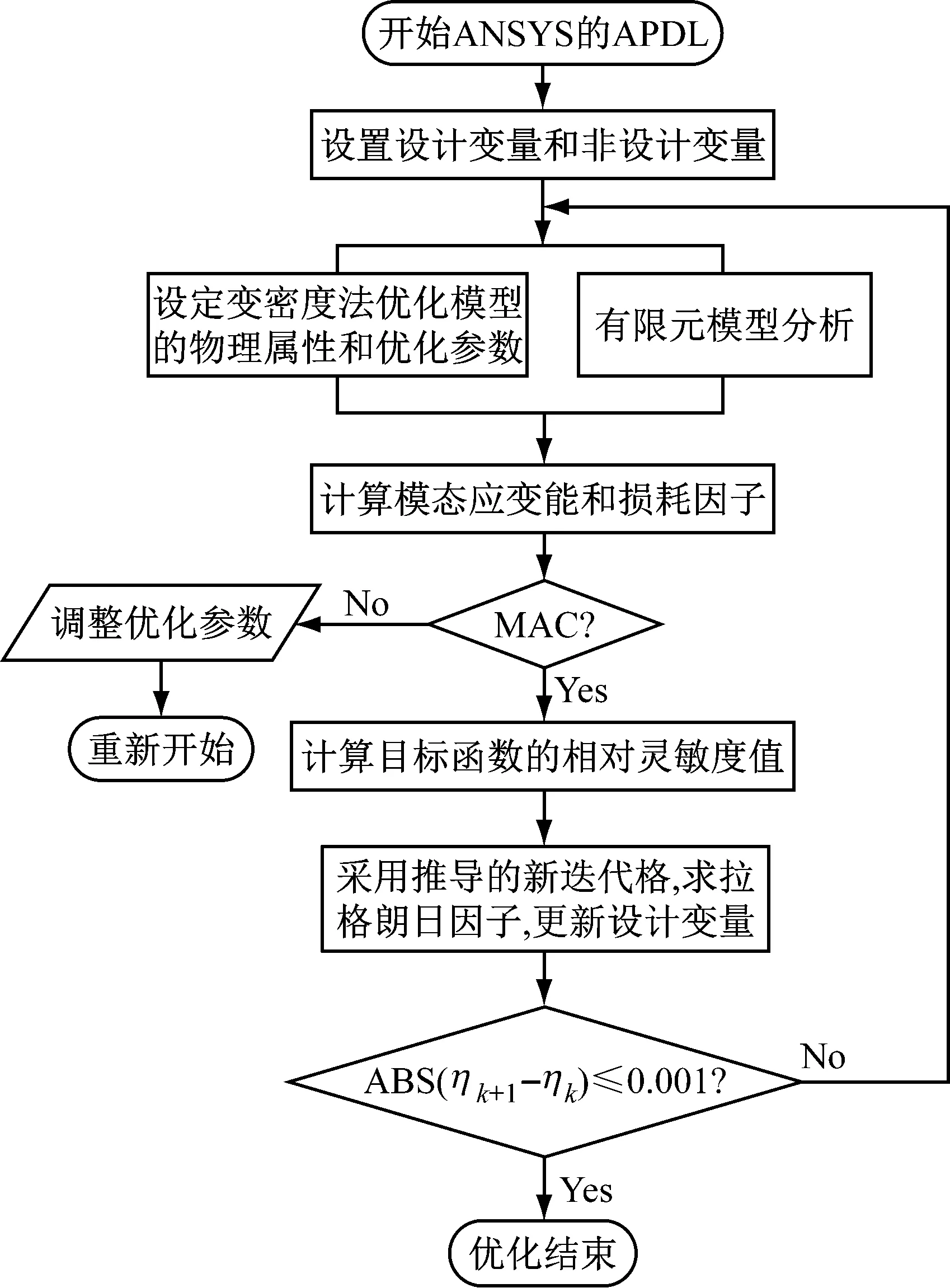
圖1 約束阻尼結(jié)構(gòu)減振拓撲優(yōu)化實現(xiàn)流程

4 優(yōu)化算例分析

影響阻尼板拓撲優(yōu)化效果的因素主要有兩方面：一是阻尼板動力學(xué)分析模型及其求解精度；二是拓撲動力學(xué)優(yōu)化算法本身的性能之優(yōu)劣。這意味著在評析優(yōu)化算法前，須先保證阻尼板有限元動力學(xué)模型及其求解的有效性。通過大型商用軟件ANSYS的二次開發(fā)語言編寫有限元模型，由于阻尼層在結(jié)構(gòu)振動中不僅有拉伸變形，而且還有剪切變形，可選擇固體單元soild185，其余層選擇殼單元shell181，并且設(shè)置這些單元的特性項，以避免剪切鎖死和體積鎖死，充分釋放振動應(yīng)變能[13]。在保證動力學(xué)建模及求解精度基礎(chǔ)上，本文分別采用傳統(tǒng)的變密度OC法和改進OC法進行阻尼板拓撲動力學(xué)優(yōu)化計算。

在算例分析時選定矩形阻尼板作為優(yōu)化對象，該板長為800 mm,寬為400 mm；基層厚4 mm，楊氏彈性模量43.2 GPa，泊松比0.33，密度1 810 kg/m3；阻尼層厚0.001 m，剪切模量25 GPa，泊松比0.495，密度1 150 kg/m3，材料損耗因子0.58；約束層厚1.5 mm，物理屬性與基層完全相同，取單位集中力作為諧響應(yīng)分析激勵力，其作用位置如圖2(b)所示。在板的寬邊基層處定義固支約束，圖2(a)給出了優(yōu)化計算所基于阻尼板有限元模型。為便于觀察，在圖3給出了約束阻尼板的前三階計算振型和結(jié)構(gòu)的模態(tài)應(yīng)變能云圖。圖4是針對阻尼板單一振動模態(tài)進行減振動力學(xué)優(yōu)化的結(jié)果。圖4(a)、圖4(c)、圖4(e)給出了針對阻尼板前三階彎曲振動模態(tài)，采用普通變密度OC法進行優(yōu)化時黏單層元密度迭代結(jié)果。圖4(b)、圖4(d)、圖4(f)則是采用改進算法得到的密度分布圖。對比兩種算法所得到的結(jié)果，不難發(fā)現(xiàn)采用改進OC法時單元的密度值的聚集度更高，即設(shè)計變量密度值要么趨近于1，要么趨近于0，密度值取中間值單元相對較少。可見，改進算法避免了中間密度的大量出現(xiàn)，基本避免了優(yōu)化迭代結(jié)果二義性問題，較好地體現(xiàn)拓撲優(yōu)化針對材料進行挖空或保留作合理取舍的算法本質(zhì)。

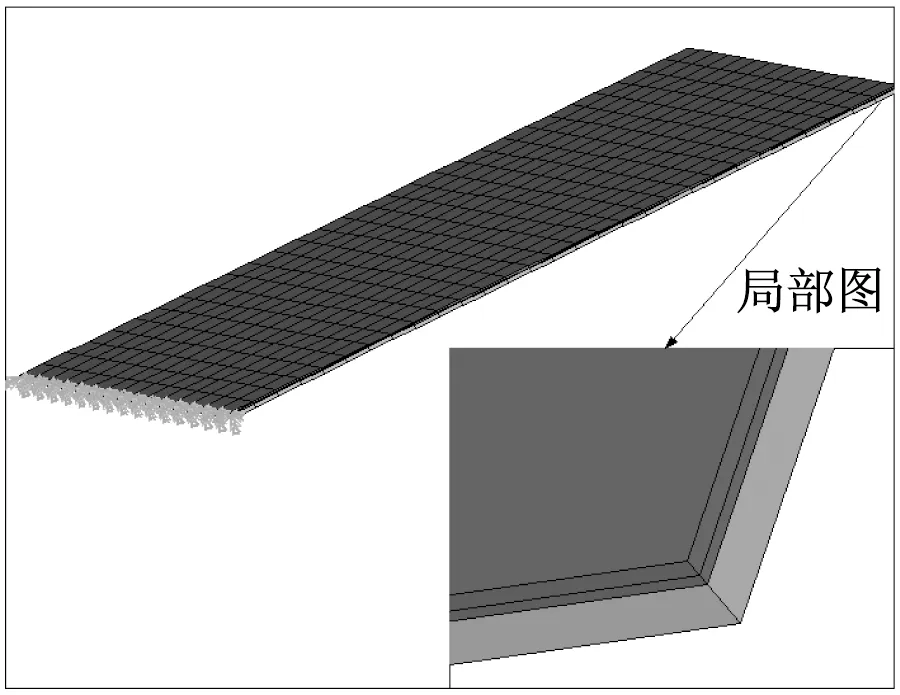
(a) 有限元網(wǎng)格劃分

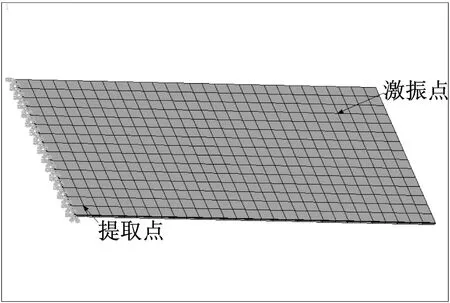
(b) 振動激勵點設(shè)定

圖2 約束阻尼板的動力學(xué)分析ANSYS模型

Fig.2 An FEM dynamic model for the damping plate

(a) 一階振型

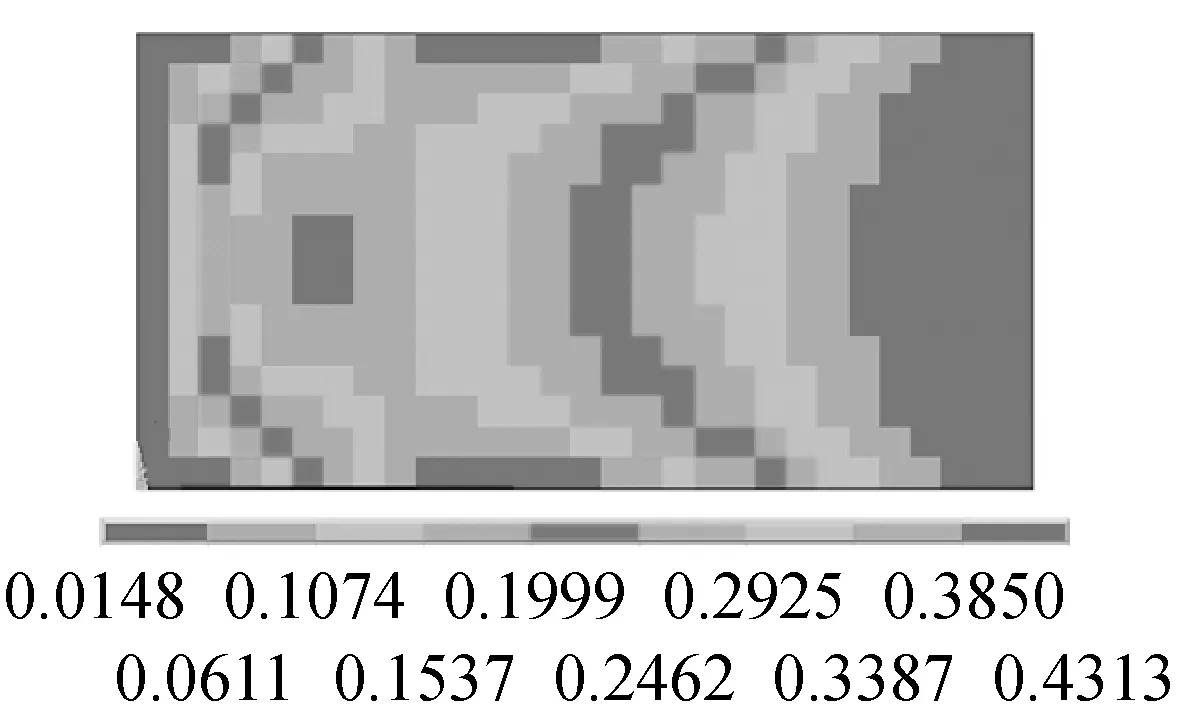
(b) 一階應(yīng)變能

(c) 二階振型

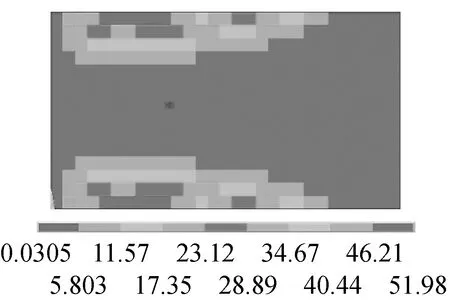
(d) 二階應(yīng)變能

(e) 三階振型

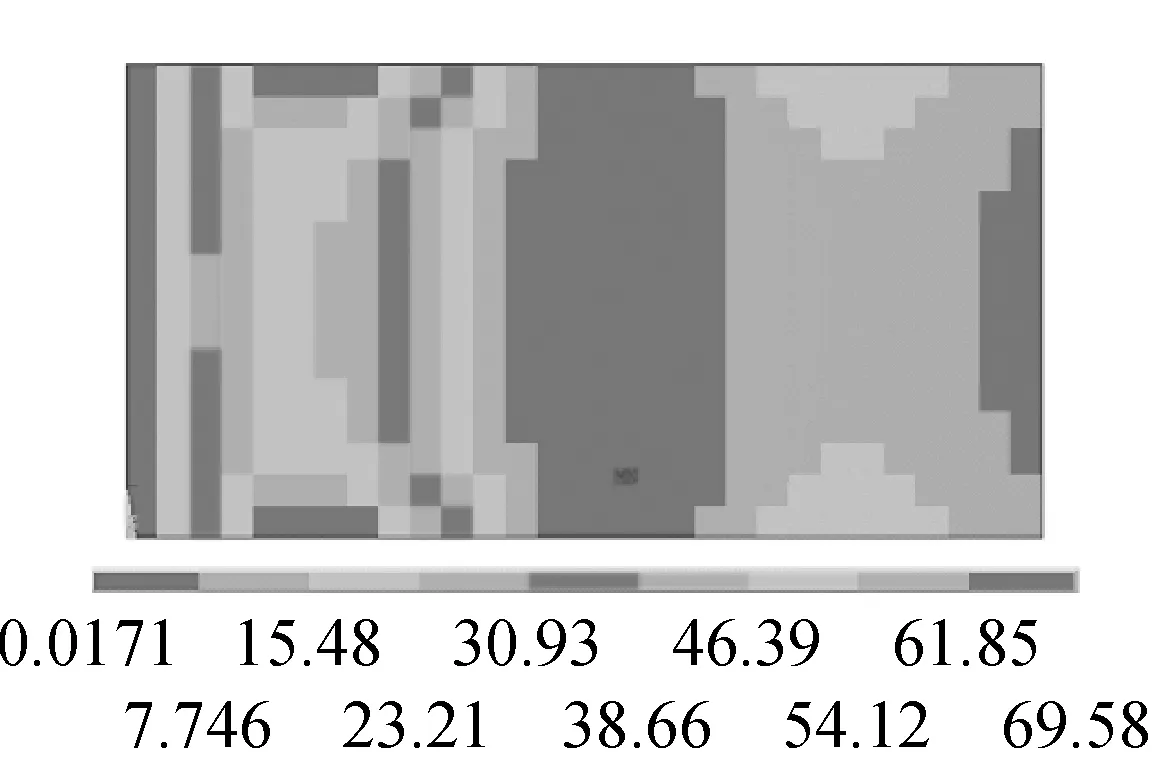
(f) 三階應(yīng)變能

圖3 約束阻尼板前三階彎曲模態(tài)振型和模態(tài)應(yīng)變能

Fig.3 Three bending modes of damped plate and their strain energy

由圖4可知，密度值較大的黏彈阻尼(需保留)單元，優(yōu)先分布于阻尼板模態(tài)應(yīng)變相對較大的位置上，而密度小的挖空單元則多半處于模態(tài)應(yīng)變較小的位置。之所以呈現(xiàn)出此布局主要是因為阻尼板模態(tài)應(yīng)變能較小處的黏彈單元變形較小，故能量耗散能力相對較弱。從這個意義上講，為提高阻尼材料的減振效能并控制其材料用量，應(yīng)優(yōu)先刪除結(jié)構(gòu)中的小應(yīng)變單元。由此可見，改進變密度法OC法優(yōu)化結(jié)果與上述定性分析結(jié)果是吻合的。

圖5給出了針對單階振動模態(tài)進行減振優(yōu)化的阻尼板的拉格朗日體積約束系數(shù)迭代。從圖中看出，雖然采用一般OC法和改進OC法均能保證體積約束系數(shù)迭代收斂，但后者的變化范圍相對更大。它表明改進OC法可在更大范圍內(nèi)的搜索約束系數(shù)，能更好地保證優(yōu)化解的全域性。圖6和圖7給出優(yōu)化迭代中的固有頻率和模態(tài)損耗因子變化。可見兩算法在經(jīng)過一定次數(shù)迭代后使頻率和模態(tài)損耗因子均收斂到最佳值，但改進OC法的收斂速度更快。

為驗證結(jié)構(gòu)單階模態(tài)拓撲動力學(xué)優(yōu)化的減振效果，分別對優(yōu)化前的阻尼板(阻尼層與約束層全覆蓋)和優(yōu)化后的阻尼板進行諧響應(yīng)特性分析。圖8給出了阻尼板的幅-頻特性曲線。從圖中看出，當(dāng)僅針對第一階彎曲振動模態(tài)進行優(yōu)化時，一階模態(tài)的振動響應(yīng)幅值明顯下降，且在采用改進算法優(yōu)化時，振幅下降量更大。還可看出，采用改進優(yōu)化算法時，一階模態(tài)頻率變化很小且不會引起峰值振蕩。

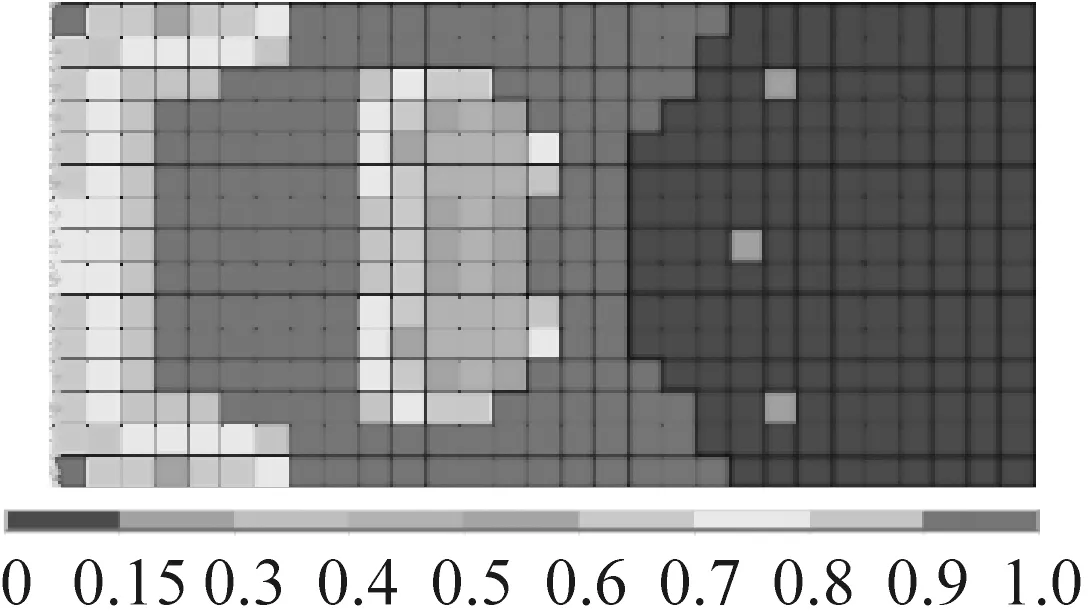
(a) 一般法一階模態(tài)優(yōu)化

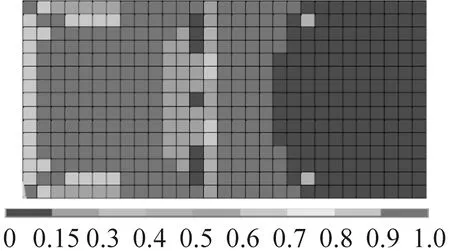
(b) 改進法一階模態(tài)優(yōu)化

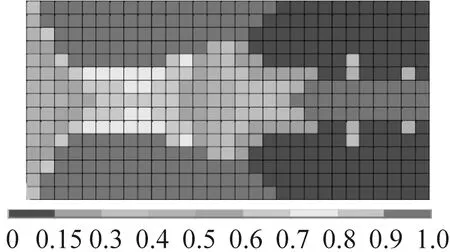
(c) 一般法二階模態(tài)優(yōu)化

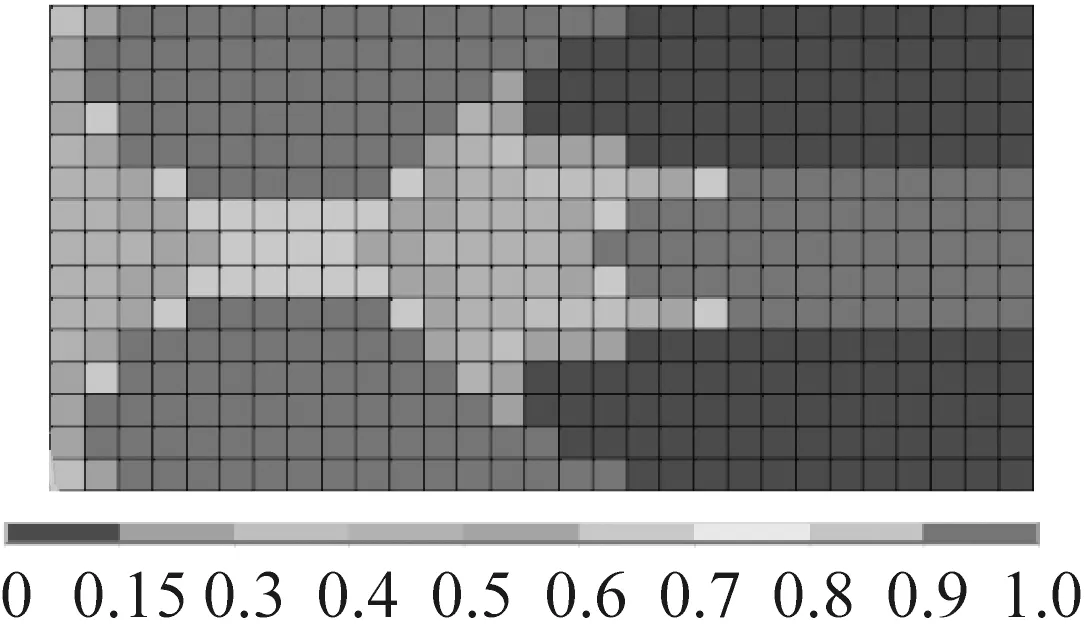
(d) 改進法二階模態(tài)優(yōu)化

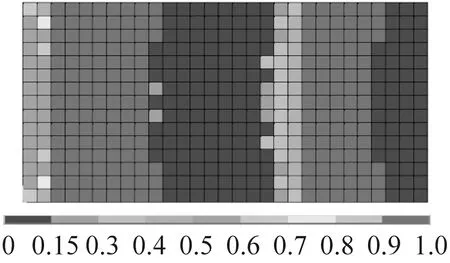
(e) 一般法的三階模態(tài)優(yōu)化

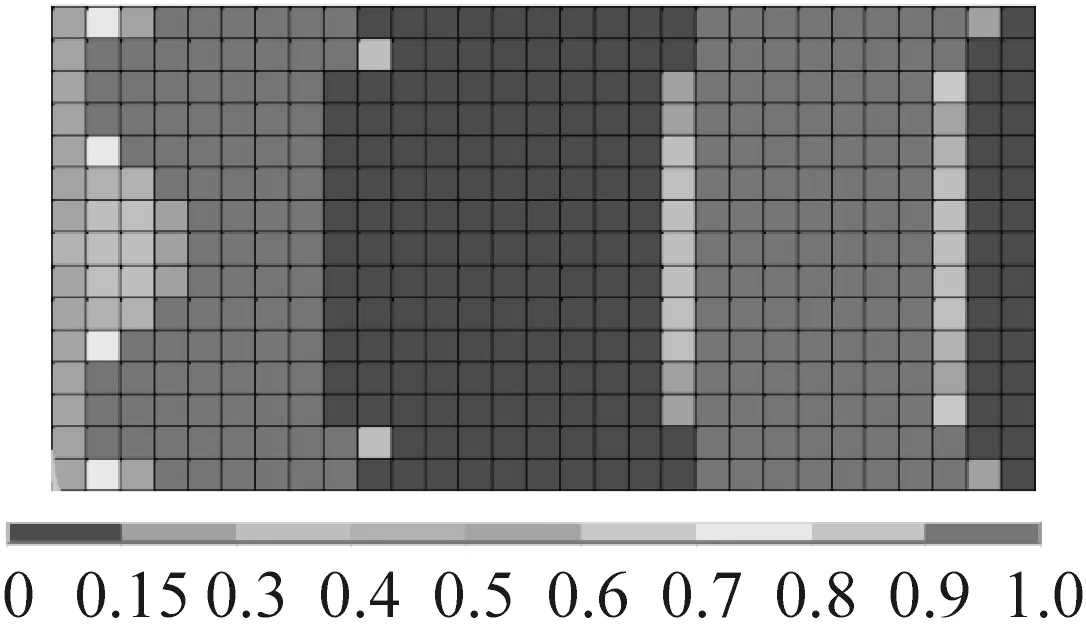
(f) 改進法的三階模態(tài)優(yōu)化

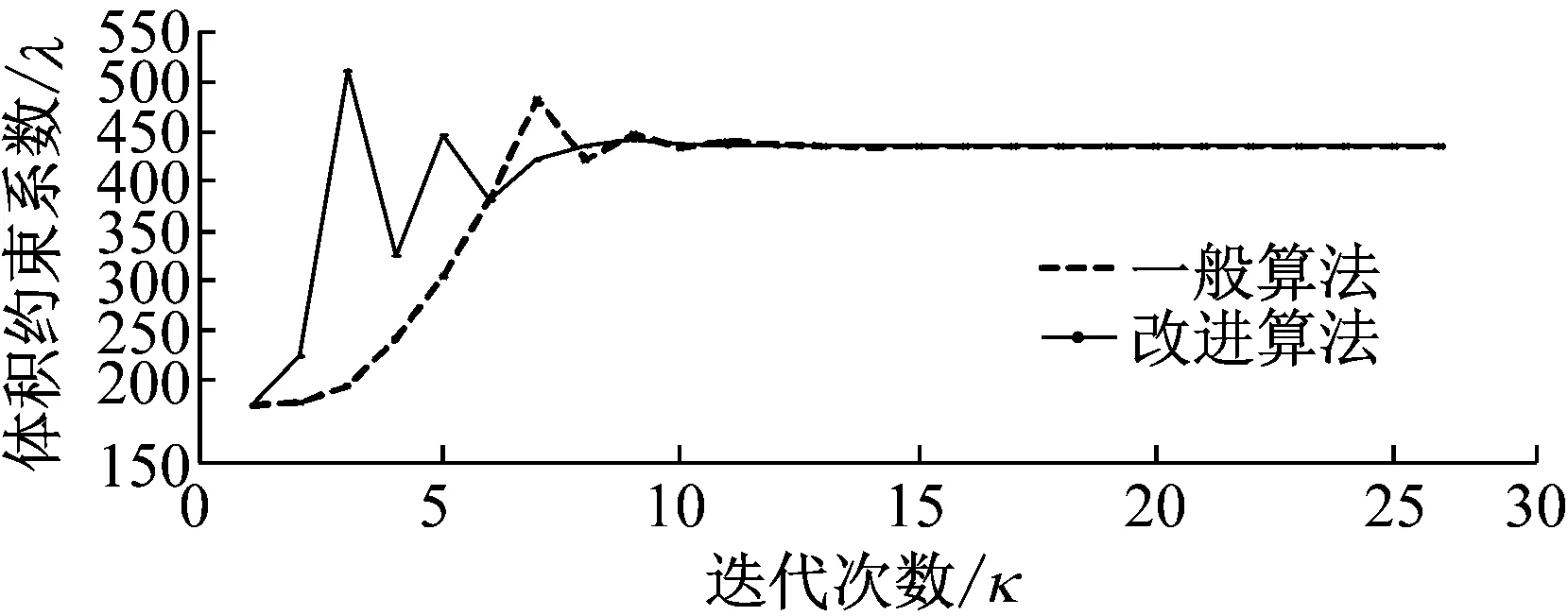
圖5 體積約束系數(shù)迭代過程

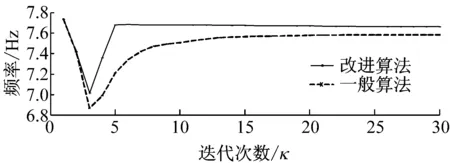
圖6 一階固有頻率迭代過程

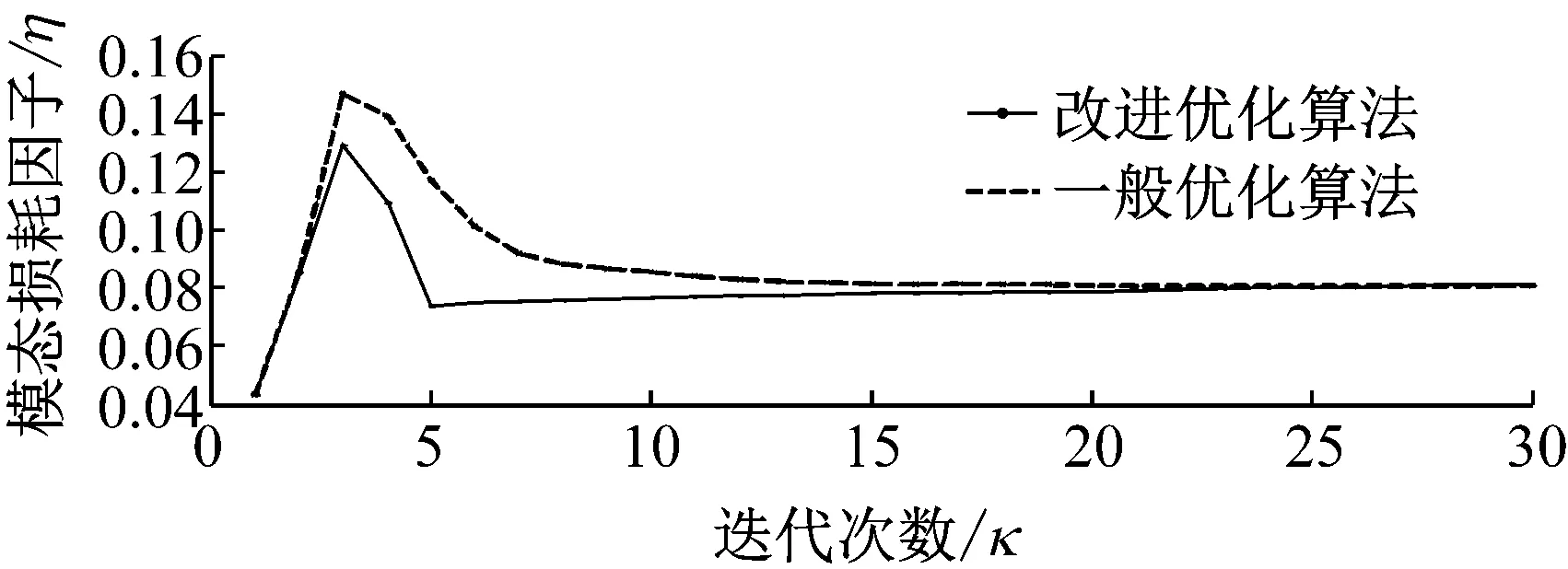
圖7 一階模態(tài)損耗因子的迭代進程

根據(jù)振動理論，結(jié)構(gòu)的振動位移響應(yīng)通常為多模態(tài)振動的線性組合。對于大多數(shù)機械結(jié)構(gòu)而言，若只針對單一模態(tài)實施減振設(shè)計，減振效果不一定理想。對于工作于高速、動載的機器，因結(jié)構(gòu)受到較寬頻域振動激勵，若只對結(jié)構(gòu)個別模態(tài)進行振動優(yōu)化，則更難使結(jié)構(gòu)獲得綜合減振效果。事實上，即使是一般運行狀態(tài)下的簡單機械，多模態(tài)振動也是其承力件的基本運動狀態(tài)。可見，針對多模態(tài)做減振設(shè)計更有價值。為此，本文針對阻尼板前三階彎曲模態(tài)，進行復(fù)合減振優(yōu)化。圖9給出了阻尼板多模態(tài)復(fù)合優(yōu)化時阻尼材料密度迭代結(jié)果。從圖中看出，低密度阻尼材料主要分布于前三階模態(tài)的公共最小模態(tài)應(yīng)變區(qū)或稱綜最小合應(yīng)變區(qū)。相反，高密度阻尼材料則分布于公共的大模態(tài)應(yīng)變區(qū)。還可看到，雖然通過改進OC法與一般OC法求得的阻尼材料密度分布情形比較相似，但改進法求得的拓撲變量值更聚集于設(shè)計變量值域的兩端，一般算法得到的中間密度值單元則更多。

圖8 一階彎曲模態(tài)優(yōu)化前后諧響應(yīng)特性對比

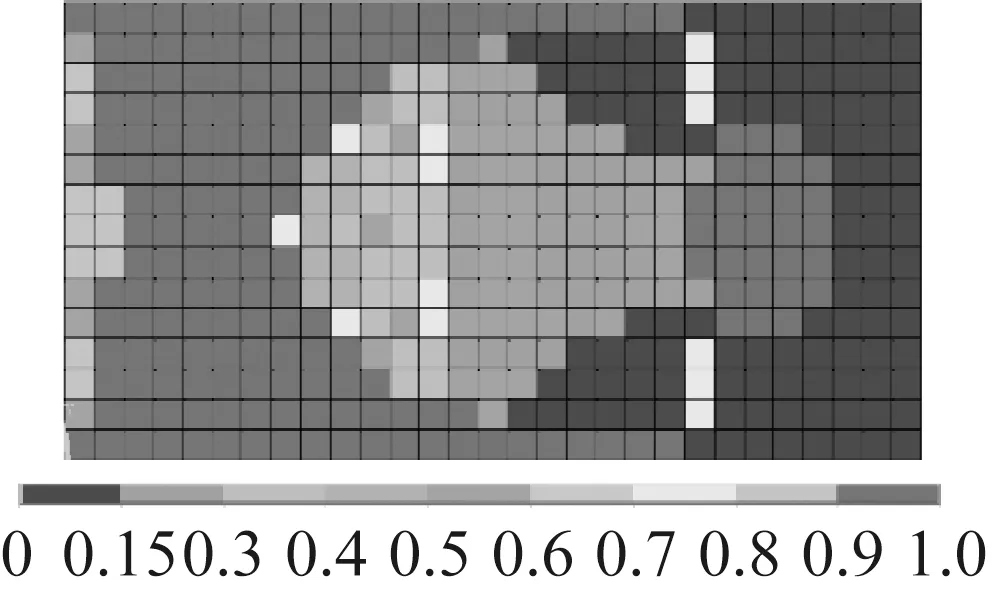
(a) 一般法密度密度分布

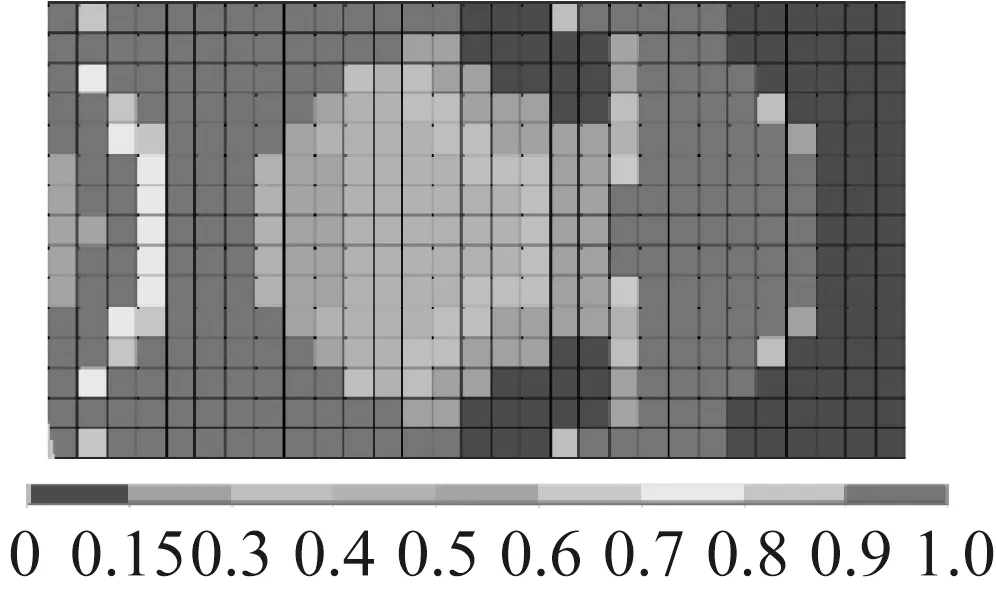
(b) 改進法密度分布

表1列出了阻尼板多模態(tài)復(fù)合振動優(yōu)化結(jié)果。可見，盡管優(yōu)化后的黏彈阻尼材料只及優(yōu)化前的一半左右，但各階模態(tài)損耗因子均有較大幅度增長。這令人疑惑，因在一般的理解中都認(rèn)為，更多地鋪設(shè)黏彈層材料對結(jié)構(gòu)減振效果更好。這對于自由阻尼結(jié)構(gòu)減振設(shè)計也許是正確的，但對于約束阻尼結(jié)構(gòu)，因在黏彈層外還需對應(yīng)地鋪設(shè)一層約束材料，黏彈層與約束層之間的質(zhì)量、剛度、損耗因子等多方面的匹配都對結(jié)構(gòu)減振效果產(chǎn)生影響，故全域的鋪設(shè)黏彈材料及約束材料并不一定獲得最佳減振效果。由表1可知，優(yōu)化結(jié)構(gòu)的一階模態(tài)損耗因子增幅達一倍以上，這一點對結(jié)構(gòu)減振特別有意義。因為多數(shù)機器在啟動時均需穿越一階頻率，并對結(jié)構(gòu)一階模態(tài)進行激勵，而且一階模態(tài)往往是對結(jié)構(gòu)振動位移響應(yīng)貢獻最大的模態(tài)，故有效抑制一階模態(tài)可大幅提高結(jié)構(gòu)總體減振效果。另外，改進OC優(yōu)化法求得的一階、三階損耗因子均較一般法要大，表明按改進法對彈性阻尼材料進行優(yōu)化布局時，阻尼板減振效果將會更好。

表1 優(yōu)化前后多模態(tài)復(fù)合優(yōu)化模態(tài)損耗因子對比

圖10給出了多模態(tài)復(fù)合優(yōu)化迭代中體積約束系數(shù)變化。可見，復(fù)合模態(tài)優(yōu)化與單一模態(tài)優(yōu)化時的體積約束系數(shù)變化趨勢大致相同。圖11則給出了多模態(tài)優(yōu)化迭代過程中，結(jié)構(gòu)前三階頻率的變化。可見，兩種迭代方法得到的各階頻率均滿足約束條件，并且迭代過程均趨于穩(wěn)定。圖12給出了多模態(tài)優(yōu)化中目標(biāo)函數(shù)的變化情況。同樣可見，兩種算法的結(jié)果均具收斂性，但改進算法求得的目標(biāo)函數(shù)值在經(jīng)過5次起伏后，便趨于穩(wěn)定，而一般OC法則要經(jīng)10次以上跌宕才逐漸進入穩(wěn)定狀態(tài)，這說明改進算法尋優(yōu)效率更高。

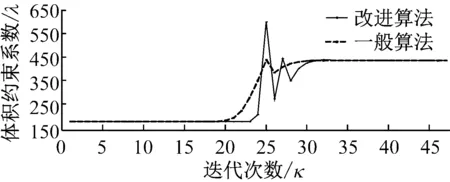
圖10 多模態(tài)體積約束系數(shù)λ迭代過程

為了驗證改進法多模態(tài)拓撲優(yōu)化的減振效果，對阻尼板進行了諧響應(yīng)分析和計算。圖13給出了阻尼板優(yōu)化前后的幅頻特性曲線。由圖13可知，采用改進法針對前三階模態(tài)的復(fù)合振動進行優(yōu)化后，這三階模態(tài)振幅均不同程度地下降，這就表明了多模態(tài)復(fù)合優(yōu)化的有效性。由圖13可知，優(yōu)化后一階模態(tài)振幅下降一倍多、二階振幅與優(yōu)化前基本持平、三階模態(tài)則大幅下降。這也正好印證表1計算結(jié)果的合理性，進一步說明了改進OC法的有效性、可行性。由圖13還可知，改進算法的抑制峰值的能力總體上要優(yōu)于一般優(yōu)化算法。

圖11 多目標(biāo)固有頻率迭代過程

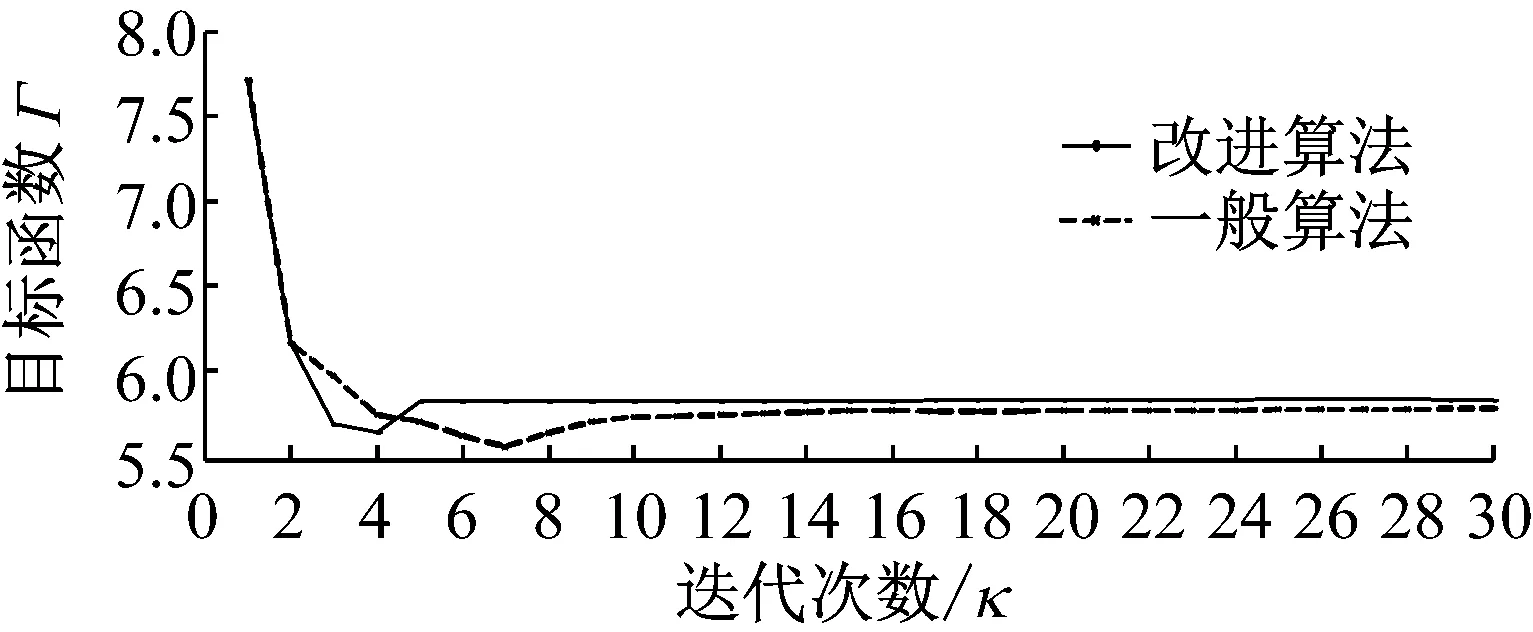
圖12 多模態(tài)目標(biāo)函數(shù)的迭代過程

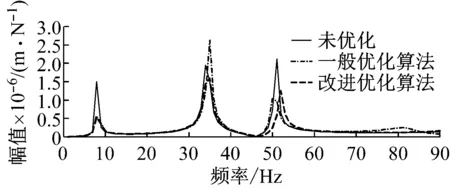
圖13 多模態(tài)優(yōu)化前后諧響應(yīng)分析

5 結(jié) 論

本文探索了約束阻尼結(jié)構(gòu)的黏彈阻尼材料的OC法優(yōu)化布局問題，發(fā)現(xiàn)了一般OC法在動力學(xué)優(yōu)化中存在的問題，并嘗試地解決了這些問題，取得了一定進展，得到以下結(jié)論：

(1) 針對一般優(yōu)化準(zhǔn)則法在求解動力學(xué)優(yōu)化問題時可能造成目標(biāo)函數(shù)靈敏度被迭代成非正值的情況，提出一種改進OC法。該方法通過對靈敏度作∞-范數(shù)計算，確保了優(yōu)化迭代的全域?qū)?yōu)特性。

(2) 實現(xiàn)了基于改進OC法約束阻尼板拓撲動力學(xué)優(yōu)化求解，得到了合理的黏彈阻尼材料和約束材料布局，并使約束阻尼結(jié)構(gòu)獲得了更佳減振效果。

(3) 改進OC法的優(yōu)化迭代過程更穩(wěn)定、尋優(yōu)效率更高，優(yōu)化結(jié)果更具全域性、更合理。

[1] BAKER M. Analysis method to support design for damp-ing[J].Engineering with Computer, 2007, 23(1):1-10.

[2] 王明旭，陳國平. 基于變密度方法約束阻尼層動力學(xué)性能優(yōu)化[J]. 南京航空航天大學(xué)學(xué)報,2010,42(3):283-287.

WANG Mingxu, CHEN Guoping. Dynamics performance optimization of constrained damping layer using variable density method[J].Journal of Nanjing University of Aeronautics & Astronautics, 2010,42(3):283-287.

[3] 蔣亞禮，呂林華，楊德慶. 提高船用阻尼材料應(yīng)用效果的優(yōu)化設(shè)計方法[J]. 中國艦船研究，2012,7(4):48-53.

JIANG Yali, Lü Linhua, YANG Deqing. Design methods for damping materials applied to ships[J]. Chinese Journal of Ship Research, 2012,7(4):48-53.

[4] 楊德慶. 動響應(yīng)約束下阻尼材料配置優(yōu)化的拓撲敏度法[J]. 上海交通大學(xué)學(xué)報，2003,37(8): 1209-1212.

YANG Deqing. Topological sensitivity method for the optimal plancement of unconstrained damping materials under dynamic response constraints[J]. Journal of Shanghai Jiao Tong University, 2003,37(8):1109-1212.

[5] 韋勇，陳國平. 一般阻尼結(jié)構(gòu)的模態(tài)阻尼比優(yōu)化設(shè)計[J]. 振動工程學(xué)報，2006, 19(4): 433-437.

WEI Yong, CHEN Guoping. Modal damping optimization for general damped structure[J]. Journal of Vibration Engineering, 2006, 19(4): 433-437.

[6] 李攀，鄭玲，房占鵬. SIMP插值的約束層阻尼結(jié)構(gòu)拓撲優(yōu)化[J].機械科學(xué)與技術(shù)，2014,33(8):1122-1126.

LI Pan, ZHENG Ling, FANG Zhanpeng. Topology optimization of constrained layer damping structue based on SIMP interpolation method[J]. Mechanical Science and Technology for Aeropace Engineering, 2014,33(8):1122-1126.

[7] BENDSOE M P, SIGMUND O. Topology optimization: theory, method and application[M].2nd ed. Berlin:Springer Verlag,2003.

[8] 郭中澤，陳裕澤. 基于準(zhǔn)則法的阻尼結(jié)構(gòu)拓撲優(yōu)化[J]. 宇航學(xué)報，2009, 30(6): 2387-2391.

GUO Zhongze, CHEN Yuze. Topology optimization of the damping structurewith optimal criteria[J]. Journal of Astronautics, 2009, 30(6): 2387-2391.

[9] 鄭玲，謝熔爐，王宜. 基于優(yōu)化準(zhǔn)則的約束阻尼材料優(yōu)化配置[J]. 振動與沖擊，2010，29(11):156-159.

ZHENG Ling, XIE Ronglu, WANG Yi, et al. Optimal placement constrained damping material in structures based on optimality criteria[J]. Journal of Vibration and Shock, 2010，29(11):156-159.

[10] JOHNSON C D, KIENHOLZ D A. Finite element prediction of damping in structures with constrained viscoelastic layers[J]. AIAA Journal, 1982, 20(9):1284-1290.

[11] MA Z D, KIKUCHI N, HAGIWARA I. Structural topology and shape optimization for a frequency response problem[J]. Computational Mechanics, 1993,13(3):157-174.

[12] 王慧彩，趙德有. 黏彈性阻尼夾層板動力特性分析及其試驗研究[J]. 船舶力學(xué)，2005, 9(4):109-118.

WANG Huicai, ZHAO Deyou. Dynamic analysis and experiment of viscoelastic damped sandwich plate[J]. Journal of Ship Mechanics, 2005, 9(4):109-118.

[13] AMICHI K, ATALLA N. A new 3D finite element for sandwich structures with a viscoelastic core[C]//Canadian Acoustics Association Conference. Montreal: Canadian Acoustics, 2007:197-198.

Topology optimization of plates with constrained damping based on improved optimal criteria

HE Honglin, YUAN Weidong, XIA Ziqiang, LIU Yaodi

(School of Aeronautical Manufacturing, Nanchang Hangkong University, Nanchang 330063, China)

A dynamic topology optimization for plates with constrained damping was conducted to provide a theoretical basis for vibration reduction design. Taking maximizing plate’s multi-modal loss factor as an objective, and taking amount of damping material, frequency equation and frequency region, and MAC factor as constraints, a topology optimization model was developed. The penalty factors for mass matrix were introduced, and the multi-modal loss factor sensitivity was deduced. Considering optimal objective function being non-convex, using a common optimal criterion might lead to the topological variables to be negative, or the optimization calculation to fall into a local optimization. So a moving asymptotic technique of mathematical programming was adopted to improve the common optimal criterion. With the improved criterion, all topological variables were brought into the optimization process so as to avoid the occurrence of local optimization. Dynamic optimization for the plates based on improved optimal criterion method were simulated. The results showed that a more reasonable constrained damping layer’s configuration is obtained with the improved method and algorithm, the plates with constrained damping achieve a better vibration reduction effect; the improved method has a better iteration stability and a faster optimization speed, and can more effectively provide a global optimal solution.

plate with constrained damping; multi-modal loss factor; improved optimal criteria method; vibration reduction characteristics; dynamic topology optimization

國家自然科學(xué)基金(51265040);國家自然科學(xué)基金(51565039)

2015-11-18 修改稿收到日期：2016-03-04

賀紅林 男,博士,教授,1967年生 E-mail:Hehonglin1967@163.com

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.09.004