淺談數(shù)學(xué)的語(yǔ)法結(jié)構(gòu)及其人文特征

廖基定+王會(huì)蘭+劉冬元

摘要：數(shù)學(xué)是一門科學(xué)，也是一種語(yǔ)言。數(shù)學(xué)的語(yǔ)法結(jié)構(gòu)表現(xiàn)為通過(guò)邏輯連詞、量詞、否定、自由和約束等語(yǔ)法生成的基本概念（如集合、函數(shù)、關(guān)系及二元運(yùn)算等）；數(shù)學(xué)的人文特征表現(xiàn)為三種形態(tài)：學(xué)術(shù)形態(tài)、生活形態(tài)及教育形態(tài)。學(xué)術(shù)形態(tài)上“冰冷而美麗”；生活形態(tài)上“樸素而動(dòng)人”；教育形態(tài)上需要引發(fā)“火熱的思考”。幫助學(xué)生數(shù)學(xué)地理解、數(shù)學(xué)地表達(dá)是數(shù)學(xué)教育的重要目標(biāo)。在教學(xué)中引入生活形態(tài)的數(shù)學(xué)語(yǔ)言可以激發(fā)學(xué)生的“火熱思考”。

關(guān)鍵詞：數(shù)學(xué)語(yǔ)言；語(yǔ)法結(jié)構(gòu)；人文特征

中圖分類號(hào)：G642.0 文獻(xiàn)標(biāo)志碼：A 文章編號(hào)：1674-9324（2017）19-0098-04

引言

美國(guó)數(shù)學(xué)家M.克萊因說(shuō)：“音樂(lè)能激發(fā)或撫慰情懷，繪畫使人賞心悅目，詩(shī)歌能動(dòng)人心弦，哲學(xué)使人獲得智慧，科技可以改善物質(zhì)生活，但數(shù)學(xué)卻能提供以上一切。”這段話一方面闡述了數(shù)學(xué)作為一種文化幾乎滲透到了世界的每個(gè)角落，另一方面也說(shuō)明了數(shù)學(xué)是一種表達(dá)世界的模式，故有科學(xué)王國(guó)的“女王”之稱。數(shù)學(xué)家卡爾森（A.Coulsbn）也曾這樣寫道：“數(shù)學(xué)是一種語(yǔ)言，具有一種語(yǔ)言的所有魅力和用處，但是它比更傳統(tǒng)的語(yǔ)言還多了一條優(yōu)點(diǎn)，即它是一種可以對(duì)我們的世界給出任何科學(xué)描述的語(yǔ)言。”因此，幫助學(xué)生數(shù)學(xué)地理解、數(shù)學(xué)地表達(dá)是數(shù)學(xué)教育的重要目標(biāo)。美國(guó)數(shù)學(xué)教師全國(guó)委員會(huì)也將“學(xué)會(huì)數(shù)學(xué)地交流”列為學(xué)校數(shù)學(xué)教育的五個(gè)基本目標(biāo)之一。

對(duì)于“數(shù)學(xué)語(yǔ)言”及“數(shù)學(xué)教學(xué)語(yǔ)言”，國(guó)內(nèi)外已有一些學(xué)者對(duì)它們進(jìn)行了一些很有意義的研究，但大多集中在對(duì)“數(shù)學(xué)語(yǔ)言”及“數(shù)學(xué)教學(xué)活動(dòng)中的語(yǔ)言”的“主要特征”的描述之上，很少有人對(duì)作為語(yǔ)言的數(shù)學(xué)之語(yǔ)法結(jié)構(gòu)進(jìn)行系統(tǒng)地剖析（這也是非常困難的）。下面我們從數(shù)學(xué)的語(yǔ)言屬性粗淺地談?wù)剶?shù)學(xué)的語(yǔ)法結(jié)構(gòu)及其主要的人文特征，以期更好地理解與欣賞數(shù)學(xué)文化內(nèi)涵，從而更有成效地進(jìn)行數(shù)學(xué)教育。

一、數(shù)學(xué)語(yǔ)言及語(yǔ)法

具體地說(shuō)，數(shù)學(xué)語(yǔ)言是表達(dá)數(shù)量、空間形式的性質(zhì)和相互關(guān)系的符號(hào)體系，或者說(shuō)是由數(shù)學(xué)符號(hào)、數(shù)學(xué)術(shù)語(yǔ)和經(jīng)過(guò)改造的自然語(yǔ)言組成的符號(hào)語(yǔ)言。數(shù)學(xué)語(yǔ)言與普通語(yǔ)言有很多相似的地方，比如“詞類”“語(yǔ)法”等要素。《普林斯頓數(shù)學(xué)指南》中，作者提出數(shù)學(xué)語(yǔ)言是由基本概念、初等邏輯外加形式化的程度來(lái)刻畫的。我們循著這條思路談?wù)剶?shù)學(xué)語(yǔ)言的大致結(jié)構(gòu)。

（一）基本概念

1.集合。集合是一些對(duì)象的集體，它有一個(gè)最基本的動(dòng)詞“屬于”。數(shù)學(xué)語(yǔ)句幾乎都可以用集合的用語(yǔ)來(lái)書寫。比如，“A是什么”可用“A∈某個(gè)集合”來(lái)表達(dá)。數(shù)學(xué)上的一個(gè)大進(jìn)展是用笛卡爾坐標(biāo)來(lái)實(shí)現(xiàn)幾何與代數(shù)的互譯。比如：“圓心在原點(diǎn)（0，0），半徑為1的圓周”（幾何圖形的描述），可以用平面點(diǎn)集{（x，y）|x■+y■=1}（代數(shù)形式）來(lái)表示。顯然，幾何表示直觀、自然；代數(shù)表示簡(jiǎn)潔、抽象。集合的三種表達(dá)方式正體現(xiàn)了數(shù)學(xué)語(yǔ)言的主要模式：文字、符號(hào)、圖形。

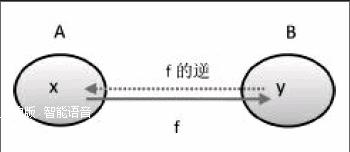
2.函數(shù)。數(shù)學(xué)上最基本的活動(dòng)之一是取出一個(gè)對(duì)象再把它變換成另一個(gè)同類或不同類的數(shù)學(xué)對(duì)象5。我們把這個(gè)過(guò)程（理解為過(guò)程）稱之為“函數(shù)”。說(shuō)f：A→B為一個(gè)函數(shù)，若記f（x）=y，則表示f把A中的元素x變成B中的對(duì)象y。要確定一個(gè)函數(shù)，必須同時(shí)確定定義域A與值域B，一個(gè)由集合A到集合B的函數(shù)就是一個(gè)規(guī)則。函數(shù)很大程度上體現(xiàn)了數(shù)學(xué)是表達(dá)現(xiàn)實(shí)世界量與量之間關(guān)系的學(xué)科屬性。如果我們把f看成過(guò)程，式子f（x）=y與y=f（x）在普通意義的語(yǔ)法上好像有點(diǎn)小區(qū)別：前者刻畫的是“將x按規(guī)則f變成了y”，強(qiáng)調(diào)的是動(dòng)作；而后者表達(dá)的是“y的值與x在規(guī)則f之下變來(lái)的值相等或一樣”，強(qiáng)調(diào)的是狀態(tài)。這樣，我們就不難理解大多數(shù)中學(xué)生，往往把函數(shù)理解為“函數(shù)值”。然而在數(shù)學(xué)上，這兩個(gè)式子并沒(méi)有區(qū)別，因?yàn)樗鼈兛坍嫷亩际且环N特殊的“等價(jià)關(guān)系”。

既然把函數(shù)看成一個(gè)過(guò)程或一種規(guī)則，若想解除函數(shù)f：A→B作用，則只要A中的x，x'不同時(shí)，f（x）與f（x'）總不同（單射）；要想找到一個(gè)函數(shù)，其作用能被f解除，則只要B中的每一個(gè)元素y都有A中的一個(gè)x滿足y=f（x）（滿射）[5]；故f存在可逆變換時(shí)，要求它既是單射又是滿射，f的逆變換仍然是一個(gè)函數(shù)。

3.關(guān)系。關(guān)系是按照某種次序組成的數(shù)學(xué)對(duì)象5，比如等價(jià)關(guān)系，從屬關(guān)系，大小關(guān)系等。數(shù)學(xué)中“關(guān)系”是數(shù)學(xué)形式化的又一體現(xiàn)。把本質(zhì)上相同的不同對(duì)象看成相同的，就避免了過(guò)多的同類。比如數(shù)學(xué)中的“等價(jià)關(guān)系”它具有自反性，對(duì)稱性與傳遞性。以此可判斷幾何中兩圖形的“相似”、模運(yùn)算中的“同余”都是等價(jià)關(guān)系。與函數(shù)概念一樣，一個(gè)關(guān)系總是與對(duì)象的一個(gè)集合關(guān)聯(lián)在一起的。如分別在集合A={2n|n=1，2，3，…}與B={3n|n=1，2，3，…}上進(jìn)行模運(yùn)算mod3，得到的結(jié)果是不同的。

事實(shí)上，數(shù)學(xué)的定義都可看成特殊的等價(jià)類。比如令A(yù)={鄰邊相互垂直的平行四邊形}，則“矩形”可看成定義在A上的等價(jià)類，當(dāng)然，它也可看成是B={對(duì)角線相等的平行四邊形}的等價(jià)類。因此可用數(shù)學(xué)語(yǔ)言表達(dá)為：矩形～A～B。在這里，等價(jià)關(guān)系是按照概念次序“是矩形”構(gòu)成的。從語(yǔ)法上說(shuō)，“關(guān)系”的詞性就像自然語(yǔ)言里的形容詞。

4.二元運(yùn)算。集合A上的一個(gè)二元運(yùn)算就是集合A上的一個(gè)函數(shù)，只是定義域是元素對(duì)所構(gòu)成的集合{（x，y）|（x，y）∈A}，比如“x+y”就可記作“+（x，y）”。當(dāng)然，在對(duì)含有一個(gè)二元運(yùn)算的句子進(jìn)行操作時(shí)，有四種性質(zhì)或要素需要考慮：可交換、可結(jié)合、定義域、恒等元或逆元，二元運(yùn)算的這些性質(zhì)是生成抽象代數(shù)基本結(jié)構(gòu)的基礎(chǔ)。

（二）初等邏輯

1.邏輯連詞。最常用的邏輯連詞是“∧（且）”“∨（或）”“？圯（蘊(yùn)含）”。記P、Q為兩個(gè)命題，比如把“他去”記作P，“你去”記作Q。“P∧Q”表達(dá)的是“當(dāng)且僅當(dāng)P、Q二者均為真時(shí)，它才為真”，即兩人都去。“P∨Q”表達(dá)的是“只要P為真或Q為真，它就真”。這里也包含了二者同時(shí)為真，與日常生活的口語(yǔ)有點(diǎn)不同。口語(yǔ)中的“他去或者你去”往往指的是兩人中的一人去，而從數(shù)學(xué)的角度看，也可以是兩人都去。

對(duì)于“P？圯Q”，數(shù)學(xué)上表達(dá)的是“只要P成立，那么Q一定成立”，也就是說(shuō)，P不成立時(shí)Q也可以成立。我們把P稱為Q的充分條件。但在日常生活中，“如果他去，你就去”往往隱含了另一層意思“如果他不去，你也不能去”。這句話容易使一些數(shù)學(xué)邏輯學(xué)得好的人鉆空子，打打擦邊球的話可以“他不去，你也去”。因此若要強(qiáng)調(diào)“如果他不去，你也不能去”，文字上可以表達(dá)為“只有他去，你才能去”；數(shù)學(xué)符號(hào)上可用“Q？圯P”來(lái)表示（P是Q的必要條件）。于是數(shù)學(xué)符號(hào)“P？圳Q”可以表達(dá)“只要他去，你就去；只有他去，你才能去”，最終兩人同時(shí)去或者同時(shí)不去。兩個(gè)互為充要條件的命題的等價(jià)性由此可見(jiàn)一斑。

2.量詞。諸如“所有的”“有一些”“任意一個(gè)”“每一個(gè)”以及“沒(méi)有一個(gè)”這樣的一些詞語(yǔ)都稱為量詞，在日常生活中，這些詞很容易產(chǎn)生歧義。下面兩句話：

“沒(méi)什么比健康快樂(lè)更重要！”——健康快樂(lè)比所有的東西都重要！

“沒(méi)什么可說(shuō)的！”——不存在東西可說(shuō)！

同樣的“沒(méi)什么”三個(gè)字含義大不一樣。一個(gè)與“所有”相關(guān)，一個(gè)與“存在”有關(guān)。在數(shù)學(xué)上，只用兩個(gè)量詞“？坌（對(duì)于所有的，對(duì)任意的一個(gè)，對(duì)每一個(gè)，forall）”和“？堝（存在，thereexist，forsome）”就表達(dá)了上述所有可能產(chǎn)生歧義的量詞。再加上連詞“使得（suchthat）”，就能把很復(fù)雜的日常語(yǔ)言或數(shù)學(xué)語(yǔ)句寫成高度符號(hào)化的形式。

“每個(gè)人都有一種愛(ài)好，就是旅游；”——證明（不一定對(duì)）

“每一個(gè)人都有一種愛(ài)好，我喜歡旅游。”——宣稱

如果記p為人，L為旅游，上面兩句話可以分別用數(shù)學(xué)符號(hào)表示為：

？坌p，？堝L∈{愛(ài)好}，s.t.p喜歡L；

？坌p，？堝a∈{愛(ài)好}，p喜歡a，我喜歡L。

當(dāng)然，現(xiàn)實(shí)中如果這樣表達(dá)的話，不免會(huì)有賣弄數(shù)學(xué)知識(shí)之嫌。

反過(guò)來(lái)，有了這兩個(gè)符號(hào)（？坌，？堝）的規(guī)定，我們也能把抽象的符號(hào)語(yǔ)言轉(zhuǎn)化為文字語(yǔ)言。比如，若令P為素?cái)?shù)集，以下兩句話均表達(dá)了素?cái)?shù)的相關(guān)性質(zhì)，但側(cè)重點(diǎn)不同。

（i）？坌n，？堝m，（m>n）∧（m∈P）；——表明了素?cái)?shù)的個(gè)數(shù)是無(wú)窮的。

（ii）？坌a，b，（ab=m）？圯（a=1）∨（b=1）；——表明了素?cái)?shù)是個(gè)只能分解為1和它本身兩個(gè)因數(shù)的數(shù)。

當(dāng)然，這里的a，b，n和m都是自然數(shù)。可見(jiàn)，量詞“？坌，？堝”都是取量于集合之上的。

3.否定。對(duì)命題P，？劭P是對(duì)P的否定。表達(dá)的是“若P為真，則？劭P不真”。數(shù)學(xué)上的否定相比于普通意義上的否定要嚴(yán)格。比如：對(duì)于命題“這個(gè)班都是女生”，若令r：人，C：這個(gè)班級(jí)，G：女孩，則可用數(shù)學(xué)符號(hào)將這句話表達(dá)為“？坌r∈C，r∈G”。而普通意義上一般有兩種否定模式，即：若把整個(gè)班級(jí)這個(gè)集合看成個(gè)體，它的否定形式為“這個(gè)班都是男生”；若把班級(jí)（集合）中的人（元素）看成個(gè)體，其否定形式為“這個(gè)班至少有一個(gè)男生”。數(shù)學(xué)上的否定是把集合中的元素看成個(gè)體，即“？劭（？坌r∈C，r∈G）”應(yīng)為“？堝x∈C，x？埸G”。在這里，我們看到了數(shù)學(xué)意義的嚴(yán)格性而避免了自然語(yǔ)言的歧義性。

4.自由和約束變項(xiàng)。代表一個(gè)可以變化的數(shù)學(xué)對(duì)象的字母稱為變項(xiàng)。可以自由表示的特定的項(xiàng)稱為自由變項(xiàng)；并不代表某一特定對(duì)象的變項(xiàng)（往往出現(xiàn)在量詞之后）稱為約束變項(xiàng)或啞變項(xiàng)[5]。比如：前面素?cái)?shù)定義（ii）中的m代表的是未曾指明的一個(gè)定數(shù)，即“任意”（自由）的素?cái)?shù)，故稱之為為自由變項(xiàng)。而等式∑■■f（m）=f（1）+f（2）+f（3）中左邊的m并不代表具體的數(shù)，但為從1到3的“這些”自然數(shù)，是約束變項(xiàng)。由于變項(xiàng)的引用，我們才發(fā)展了一種如方程式方法這樣非常有效的解決數(shù)學(xué)問(wèn)題的方法。

（三）形式化的程度

從上面看出，由幾個(gè)集合論的概念與邏輯連詞就能把通常的數(shù)學(xué)命題表示出來(lái)。一方面，數(shù)學(xué)語(yǔ)言的口語(yǔ)可能更人性化，但卻可能導(dǎo)致不可接受的不精確；另一方面，完全形式化的符號(hào)語(yǔ)言雖然簡(jiǎn)潔而準(zhǔn)確，但使人讀起來(lái)很耗費(fèi)精神。最理想的辦法是用一種對(duì)讀者友好的盡可能容易接受的語(yǔ)言表達(dá)寫作，并且確信讀者在認(rèn)為有必要的時(shí)候，能夠使寫的東西比較形式化。也就是說(shuō)，數(shù)學(xué)形式化的程度要適應(yīng)閱讀對(duì)象的數(shù)學(xué)經(jīng)驗(yàn)與訓(xùn)練水平。比如：“這個(gè)班都是女生”，如果不是在特定的數(shù)學(xué)環(huán)境之中，一般不會(huì)用“？坌r∈C，r∈G”來(lái)表示，雖然我們欣賞到了其中的簡(jiǎn)潔美、抽象美。然而，盡管文字語(yǔ)言表達(dá)可能更為直觀，當(dāng)需要運(yùn)用計(jì)算機(jī)程序來(lái)證明某個(gè)命題時(shí)，往往會(huì)追求更高程度的形式化，如“每個(gè)非空正整數(shù)集合都有一個(gè)最小元素”用數(shù)學(xué)符號(hào)語(yǔ)言可表示為：

？坌A？奐N，（？堝n∈N，n∈A）？圯？堝x∈A，？坌y∈A，s.t.（y>x）∨（y=x）.

二、數(shù)學(xué)語(yǔ)言的人文特征

上述數(shù)學(xué)語(yǔ)法的粗略介紹讓我們對(duì)數(shù)學(xué)語(yǔ)言的特性有了總體上的把握。當(dāng)然，作為一種語(yǔ)言，數(shù)學(xué)有著其獨(dú)特的人文特征。康仕慧提出的“數(shù)學(xué)的本質(zhì)是依賴語(yǔ)境的概念”表達(dá)了數(shù)學(xué)的語(yǔ)言形態(tài)與語(yǔ)境是密切相關(guān)的。這里的“語(yǔ)境”我們理解為：理論與技巧的關(guān)系、抽象與直觀的關(guān)系，基礎(chǔ)的寬厚程度，數(shù)學(xué)普及與提高的要求以及對(duì)隱藏在形形色色的公式和定理后面的精神世界如何揭示等。因此，不同“語(yǔ)境”之下的數(shù)學(xué)概念（數(shù)學(xué)對(duì)象）的表達(dá)會(huì)有一定的差別。我們沿用張奠宙先生將數(shù)學(xué)知識(shí)分為學(xué)術(shù)形態(tài)和教育形態(tài)的方法，將數(shù)學(xué)語(yǔ)言（或數(shù)學(xué)知識(shí)）分為三種形態(tài)：學(xué)術(shù)形態(tài)、生活形態(tài)與教育形態(tài)（我們?cè)谶@并不追求分法的嚴(yán)格性，因?yàn)槿N形態(tài)并不是孤立地，往往有交叉成分）。這里所說(shuō)的數(shù)學(xué)生活形態(tài)，即用生活語(yǔ)言來(lái)表達(dá)數(shù)學(xué)概念或用數(shù)學(xué)概念來(lái)表達(dá)生活原理的模式下面簡(jiǎn)要談?wù)剶?shù)學(xué)語(yǔ)言在這三種形態(tài)之下的主要特征。

（一）學(xué)術(shù)形態(tài)——簡(jiǎn)潔、精煉，高度抽象與形式化，具有規(guī)范性與通用性

與一般語(yǔ)言相比較，數(shù)學(xué)語(yǔ)言傾向于模式化、符號(hào)化，在概括數(shù)學(xué)對(duì)象及數(shù)學(xué)結(jié)構(gòu)的屬性過(guò)程中，舍去了具體事物的幾何、物理等方面的特性，只留下它的空間形式和數(shù)量關(guān)系。因此，數(shù)學(xué)語(yǔ)言更為簡(jiǎn)潔、精煉，也更為抽象與形式化。也正因?yàn)槿绱耍沟脭?shù)學(xué)成為科學(xué)世界規(guī)范而通用的語(yǔ)言成為可能。然而，數(shù)學(xué)語(yǔ)言的簡(jiǎn)潔性、抽象性所帶來(lái)的美感難免與高度形式化所帶來(lái)的冷峻相伴相生，正如H·弗賴登塔爾所描述：“沒(méi)有一種數(shù)學(xué)的思想，以它被發(fā)現(xiàn)時(shí)的那個(gè)樣子公開(kāi)發(fā)表出來(lái)。一個(gè)問(wèn)題被解決后，相應(yīng)地發(fā)展為一種形式化技巧，結(jié)果把求解過(guò)程丟在一邊，使得火熱的發(fā)明變成冰冷的美麗。”于是大多數(shù)情形之下我們感受到的是數(shù)學(xué)學(xué)術(shù)形態(tài)“冰冷的美麗”。

（二）生活形態(tài)——直觀形象，簡(jiǎn)潔深刻，容易讓人接受，但兼具模糊和不確定性

皮姆提倡的社會(huì)建構(gòu)主義學(xué)習(xí)心理學(xué)認(rèn)為，學(xué)習(xí)主要地應(yīng)被看成一種社會(huì)行為，而這不僅是指?jìng)€(gè)體與群體之間的積極互動(dòng)，而且也是指?jìng)€(gè)體對(duì)整體性文化的繼承，即人的認(rèn)知過(guò)程是一個(gè)整體，對(duì)科學(xué)的、人文的、生活的種種認(rèn)識(shí)交織在一起。將抽象的數(shù)學(xué)概念用個(gè)人已經(jīng)歷的以及精神生活之中的人文“意境”來(lái)“比喻”，能把復(fù)雜的問(wèn)題形象化；通過(guò)生活中的“原形”找到思維的契合點(diǎn)，實(shí)現(xiàn)數(shù)學(xué)思維的建構(gòu)。這些樸素而直觀的形式更能激發(fā)情感上的共鳴，也更容易使人接受。反過(guò)來(lái)，當(dāng)一個(gè)人對(duì)數(shù)學(xué)的概念有了比較深刻的理解之后，又可以用數(shù)學(xué)的語(yǔ)言來(lái)描述生活現(xiàn)象，包括人的喜怒哀樂(lè)。因此，我們能通過(guò)生活形態(tài)的數(shù)學(xué)語(yǔ)言感受到數(shù)學(xué)“動(dòng)人的樸素美”。浙江大學(xué)杰出教學(xué)貢獻(xiàn)獎(jiǎng)“心平獎(jiǎng)”獲得者數(shù)學(xué)教師蘇德礦教授應(yīng)邀在校友婚禮上的風(fēng)趣發(fā)言：“他是你的嚴(yán)格遞增函數(shù)，你的生活一天比一天幸福，一天比一天快樂(lè)，一天比一天美好，希望你們的愛(ài)情像一條射線，只有起點(diǎn)沒(méi)有終點(diǎn)。”流傳于坊間的“對(duì)你的思念是連續(xù)的”，過(guò)細(xì)工作是“微分”，取得成績(jī)是“積分”。這些言語(yǔ)貌似樸素，卻寓意深刻，增函數(shù)、射線、微分、積分的性質(zhì)均栩栩如生。當(dāng)然，“當(dāng)思想能被直觀地描述時(shí)，馬虎的語(yǔ)言是能被接受的，但是，一件事越抽象，離直觀越遠(yuǎn)，就越需要仔細(xì)的語(yǔ)言來(lái)描述”。就像上面的“微分”“積分”與數(shù)學(xué)意義上的概念還是有所區(qū)別。因此，生活形態(tài)的數(shù)學(xué)語(yǔ)言有時(shí)也難免模糊而不確定。

（三）教育形態(tài)——具有明晰性、嚴(yán)謹(jǐn)性及可接受性

數(shù)學(xué)教育是使數(shù)學(xué)作為文化，使數(shù)學(xué)促進(jìn)人自身發(fā)展的基本建設(shè)。讓學(xué)生理解數(shù)學(xué)知識(shí)、學(xué)會(huì)數(shù)學(xué)地表達(dá)客觀世界是數(shù)學(xué)教育的重要目標(biāo)。所謂數(shù)學(xué)語(yǔ)言的明晰性，就是說(shuō)，在一個(gè)具備相容性的數(shù)學(xué)系統(tǒng)內(nèi)，符號(hào)的使用不應(yīng)引起歧義，數(shù)學(xué)思維應(yīng)該流暢、迅捷而便于創(chuàng)造。所謂嚴(yán)謹(jǐn)性，就是內(nèi)容的前后銜接，定理、公式進(jìn)行嚴(yán)格的證明才能確立等。然而，過(guò)分強(qiáng)調(diào)邏輯或形式化會(huì)導(dǎo)致學(xué)習(xí)者尤其是低年級(jí)的學(xué)生難以接受。因此，數(shù)學(xué)語(yǔ)言的教育形態(tài)除了要盡量保留數(shù)學(xué)的學(xué)術(shù)形態(tài)的主要特征之外，還要考慮受教育者的接受能力。

三、“冰冷的美麗”+“動(dòng)人的樸素”→“火熱的思考”

張奠宙先生提出數(shù)學(xué)教學(xué)的目標(biāo)之一，是要把數(shù)學(xué)知識(shí)的學(xué)術(shù)形態(tài)轉(zhuǎn)化為教育形態(tài)，數(shù)學(xué)教師的任務(wù)在于返璞歸真，把數(shù)學(xué)的形式化邏輯鏈條恢復(fù)為當(dāng)初數(shù)學(xué)家發(fā)明創(chuàng)新時(shí)的火熱思考，主張將數(shù)學(xué)與人文意境想融合，構(gòu)建學(xué)生容易理解的教育形態(tài)，幫助學(xué)生理解教學(xué)內(nèi)容，從而化“冰冷的美麗”為“火熱的思考”。其宗旨就是提倡借助社會(huì)文明闡述數(shù)學(xué)的文化含義，或者說(shuō)借助于數(shù)學(xué)的人文意境即生活形態(tài)來(lái)理解數(shù)學(xué)的學(xué)術(shù)形態(tài)。這無(wú)疑是實(shí)現(xiàn)數(shù)學(xué)的教育形態(tài)化之有效途徑。如何激發(fā)學(xué)生思考的熱情是我們數(shù)學(xué)教育工作者所面臨的共同問(wèn)題。數(shù)學(xué)家歐拉倡導(dǎo)的“發(fā)現(xiàn)法”教學(xué)，主張“講課時(shí)尋點(diǎn)開(kāi)心，讓學(xué)生感到驚異”，通過(guò)教學(xué)生猜想、教學(xué)生發(fā)現(xiàn)、教學(xué)生思想，這也是將“冰冷的美麗”化為“火熱思考”的一種重要途徑，與張奠宙先生的與“人文意境相融合”有異曲同工之妙，皆強(qiáng)調(diào)的是讓學(xué)生有感情地投入。

“語(yǔ)言是一種彈性工具，在用日常語(yǔ)言表述數(shù)學(xué)事實(shí)時(shí)，必須改造它，使它適應(yīng)教學(xué)的需要9。”那么，我們?yōu)槭裁床煌ㄟ^(guò)數(shù)學(xué)語(yǔ)言的各種形態(tài)之間的巧妙結(jié)合與相互轉(zhuǎn)換，讓學(xué)生“尋點(diǎn)開(kāi)心”并“感到驚異呢”？蘇德礦教授以遙遙領(lǐng)先的票數(shù)被評(píng)為浙大最受歡迎的教師，與他善于將生活語(yǔ)言用于數(shù)學(xué)教學(xué)或者將數(shù)學(xué)概念用到生活之中是密不可分的。可以說(shuō)，“礦爺”實(shí)現(xiàn)了“冰冷的美麗”與“動(dòng)人的樸素”之巧妙結(jié)合，在一定程度上激發(fā)了學(xué)生“火熱的思考”。盡管數(shù)學(xué)語(yǔ)言的生活形態(tài)具有模糊性及不精確性，也不是每位教師都能把握好它們的“結(jié)合度”，但這一理念是值得推廣的，因?yàn)樵诤芏嗲樾沃拢⒉恍枰^(guò)分強(qiáng)調(diào)邏輯與形式化，我們關(guān)注的是數(shù)學(xué)的思想、方法和精神。

因此，如何根據(jù)受教育者的年級(jí)、專業(yè)、基礎(chǔ)，優(yōu)先考慮數(shù)學(xué)的思想、方法和精神，在此基礎(chǔ)上將數(shù)學(xué)語(yǔ)言的生活形態(tài)與學(xué)術(shù)形態(tài)有機(jī)結(jié)合再轉(zhuǎn)換為教育形態(tài)是所有數(shù)學(xué)教育者應(yīng)該努力的方向，也是我們面臨的一大難題。也許我們可以借鑒蘇德礦教授的六字育人心經(jīng)：“懂、透、精、趣、情、德。”

參考文獻(xiàn)：

[1]易南軒.數(shù)學(xué)美拾趣[M].北京：科學(xué)出版社，2008.

[2]鄭毓信.數(shù)學(xué)教育：動(dòng)態(tài)與省思[M].上海：上海教育出版社，2005.

[3]陳永明.數(shù)學(xué)教學(xué)中的語(yǔ)言問(wèn)題[M].上海：上海科技教育出版社，1998.

[4]楊之，王雪芹.數(shù)學(xué)語(yǔ)言與數(shù)學(xué)教學(xué)[J].數(shù)學(xué)教育學(xué)報(bào)，2007，16（4）：13-16.

[5]TimothyGowers主編，齊民友（譯）.普林斯頓數(shù)學(xué)指南[M].北京：科學(xué)出版社，2014.

On the Grammatical Structures and Cultural Characteristics of the Mathematics

—Talk a Little about the 'Icy Beauty' and 'Touching Simplicity' of Mathematics

LIAO Ji-ding1，WANG Hui-lan2，LIU Dong-yuan2

（1.Dean's Office，University of South China，Hengyang，Hunan 421001，China；

2. School of Mathematics and Physics，University of South China，Hengyang，Hunan 421001，China）

Abstact：Mathematics is a language as well as science. The grammatical structure of mathematics is reflected by logic conjunctions，quantifiers，negations and some free or constraint variables，which are combined with other basic concepts （such as set，function，relations and binary operation）. The form of cultural characteristics of mathematics is divided into 'academic form'，'lifestyle form' and 'educational form'. 'Academic form' seems to be 'cold and beautiful'，while 'lifestyle form' seems to be 'simple and touching' and educational form need stimulate 'hot thinking'. To help students understanding and expressing the mathematics is an important goal of mathematics education. Introducing the lifestyle language to mathematics teaching may stimulate the students to think intensively.

Key words：mathematics language；grammatical structure；cultural characteristics