ORC向心透平葉輪扭曲規律對其性能的影響

王 智， 尹立冰

(華北電力大學 電站設備狀態監測與控制教育部重點實驗室， 河北保定 071003)

ORC向心透平葉輪扭曲規律對其性能的影響

王 智， 尹立冰

(華北電力大學 電站設備狀態監測與控制教育部重點實驗室， 河北保定 071003)

以環己烷為工質，進行了200 kW向心透平的熱力設計和結構設計，并采用數值模擬方法研究透平內部的流動情況，分析了透平葉輪扭曲規律對透平性能的影響.結果表明：所設計的向心透平對于跨聲速工況有著良好的流動特性，葉輪的扭曲程度會影響葉輪流道形狀和出口氣流與軸向的夾角；不同的葉輪扭曲規律下，透平輪周效率變化的最大值為2.44%，葉輪扭曲規律是葉輪結構優化設計的重要影響因素.

向心透平； 葉輪扭曲規律； 輪周效率; 熱力設計

有機工質朗肯循環發電技術在回收工業廢熱、利用太陽能和地熱能等方面發揮了重要作用.流動工質的選擇和高效透平的設計是有機朗肯循環(ORC)發電系統的重要研究內容[1].設計出符合氣體動力學并能準確達到預期輸出的膨脹機是設計階段的主要目標[2].向心透平作為有機朗肯循環發電系統中的關鍵部件，具有大焓降、小流量、高膨脹比、高效率、易于制造及結構簡單等特點，已受到越來越多的關注.在能量轉換過程中，葉輪的幾何特點和氣動特性決定了整機的性能.國內外很多學者和研究機構在向心透平設計[3-4]、內部流動損失機理[5]和氣動優化等方面進行了研究，在通過使用數學過程控制向心葉輪設計變量修改，改變和優化葉輪型線使葉輪內部流動損失降低等方面取得了一些進展[6-8].但對中低溫ORC透平的研究仍處于起步階段，還有很多待解決的技術問題[9-10].

在特定熱源條件下，烷類工質環己烷以其較高的熱效率、較低的單位功量質量流量和UA等特性，被認為是低溫余熱回收系統中較為理想的循環工質[11].

筆者以環己烷為工質，通過熱力計算和三維造型在不同葉輪扭曲規律下進行ORC發電系統向心透平的整機設計，通過改變形狀設計參數來得到葉輪的扭曲規律，分析葉輪扭曲規律對透平效率的影響.

1 有機工質向心透平設計

1.1 向心透平熱力設計

綜合考慮工質的物性特點、運行的安全性、經濟性以及透平的簡便性后，向心透平初始設計參數如表1所示.根據初始數據，通過熱力計算確定向心透平的氣動參數和基本幾何尺寸(見表2).

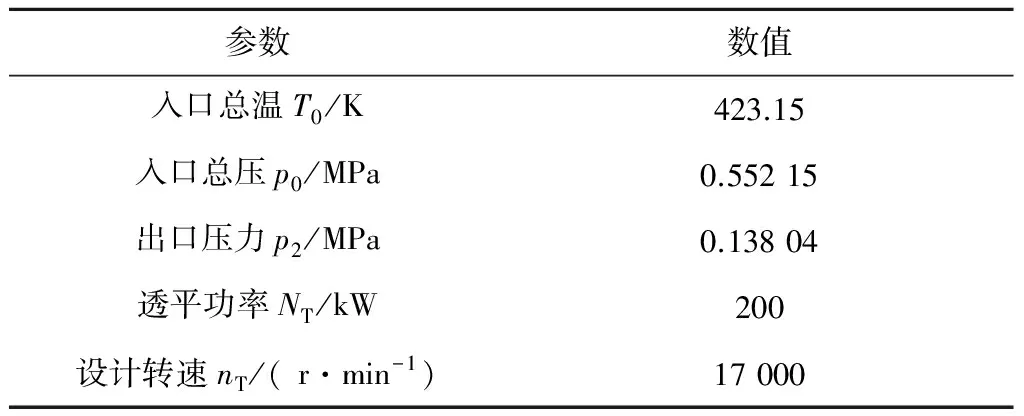
表1 初始設計參數

圖1給出了向心透平膨脹過程的焓熵圖，圖中的0*2s為向心透平中的等熵膨脹過程，工質的實際膨脹過程用0*012表示.

1.2 向心透平的造型設計

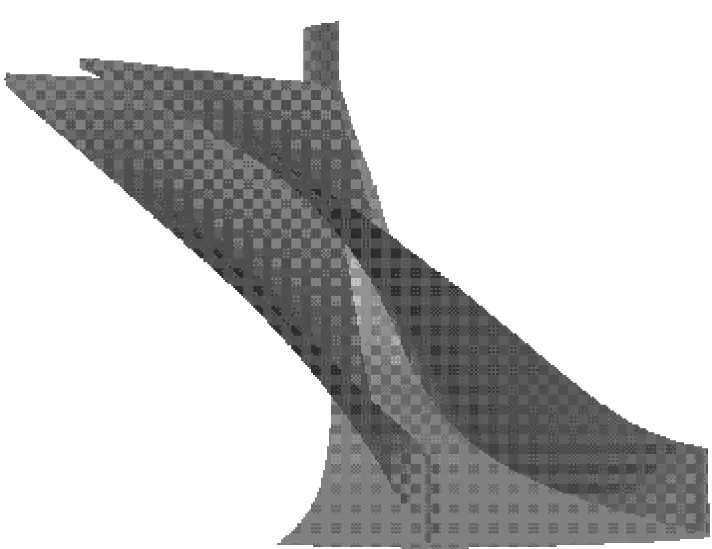
本設計方案采用TC-4P型導葉柵，利用其斜切部分達到超音速.動葉輪的造型通過控制貝塞爾曲線的控制點來確定子午面形狀，選取5個不同截面，通過空間積疊完成動葉輪的三維造型.圖2給出了靜葉和動葉三維整體造型圖.

2 數值模擬結果與分析

2.1 網格劃分及邊界條件

網格劃分采用結構化網格，網格拓撲結構為H/J/L/C-Grid型，其特點是可以根據幾何進出口角和軸向的夾角范圍合理選擇葉片通道進口和出口拓撲結構.經過網格無關性驗證后，最終網格數量采用82萬，網格示意圖見圖3.進出口邊界條件為進口總壓0.552 15 MPa、進口總溫423.15 K、出口壓力0.138 04 MPa.定義周期性邊界，無滑移壁面.動靜交界面交接類型為stage級模式.選用SST湍流模型，氣體狀態方程采用PR立方型方程，該方程在計算真實氣體物性方面平衡了簡單性和準確性[12-13].以殘差收斂到10-6為收斂標準，并監視總對總效率.

表2 向心透平的主要設計參數

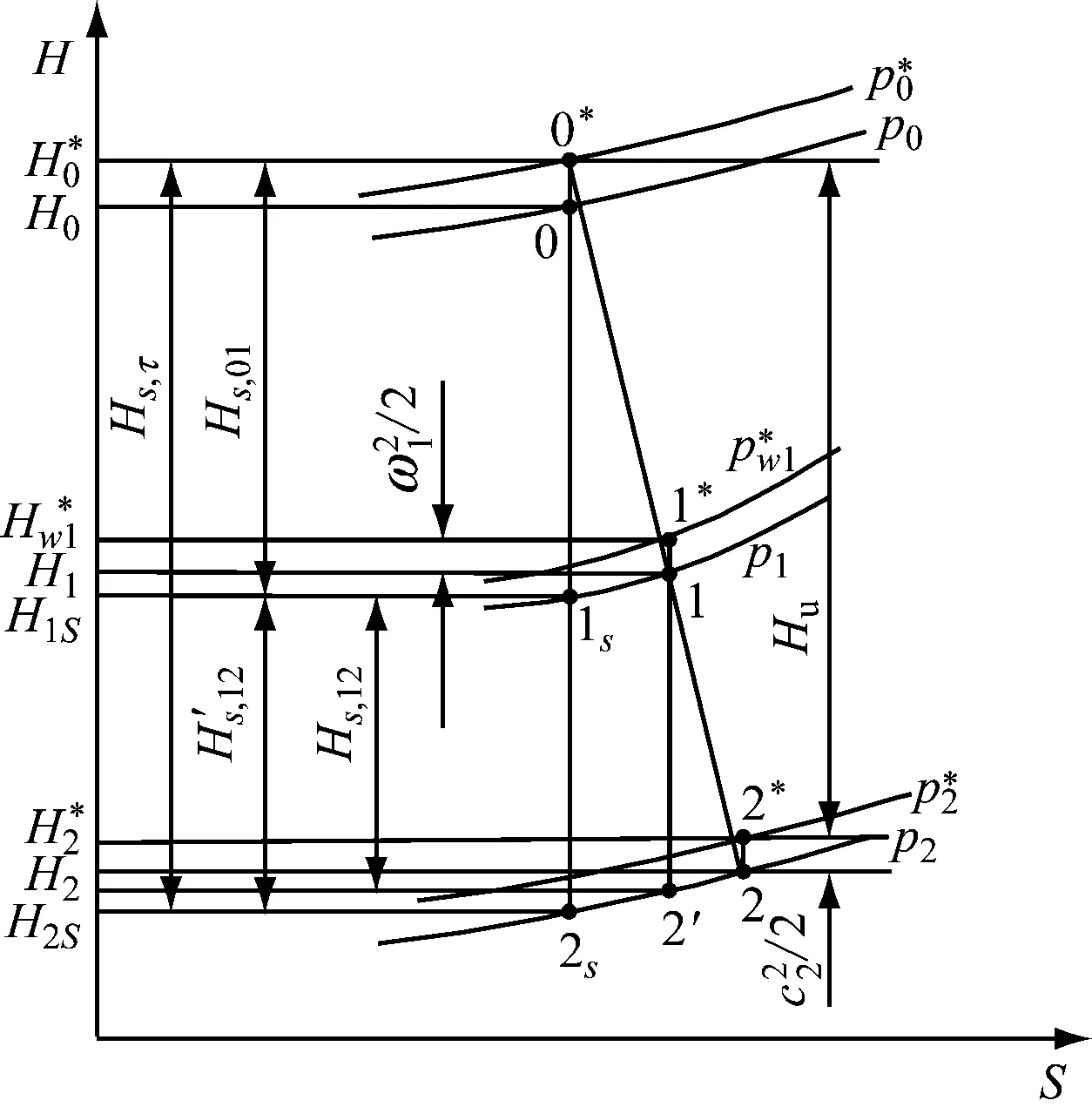
圖1 向心透平工作過程

圖2 透平三維造型圖

(a)導葉計算網格(b)葉頂間隙網格放大圖

圖3 計算網格示意圖

Fig.3 Schematic diagram of the computational grid

2.2 導葉柵模擬結果分析

圖4給出了導葉柵5%葉高、50%葉高和90%葉高處的表面靜壓分布曲線.從圖4可以看出，在壓力面基本為順壓梯度，而在吸力面上流線方向0.8～0.98處為導葉吸力面的斜切部分，此區域馬赫數大，最高達到了1.24，工質會因壓力的劇烈下降而產生過度膨脹流動過程.大約在流向0.825位置和0.93位置出現壓力突越，逆壓流動.在導葉尾部區域流線方向約0.98處出現了強逆壓梯度和激波，氣流經過激波，工質壓強、溫度和密度等參數將顯著變化，如圖5所示的50%葉高處導葉尾部密度梯度分布云圖.激波的存在擾亂了氣流的流動分布，加大了透平流動損失，因此必須控制和弱化激波強度.整體上，壓降和密度的分布較為合理，對于跨聲速工況有良好的流動特性，所選取的TC-4P型導葉柵能夠滿足工質膨脹的要求.

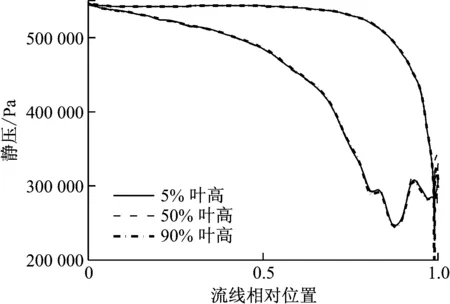
圖4 導葉柵表面靜壓分布曲線

圖5 50%葉高導葉尾部密度梯度分布云圖

2.3 不同葉輪扭曲規律對向心透平性能的影響

葉輪的扭曲規律改變將引起葉片軸向長度、葉輪出口內外徑等結構參數的改變.在保證葉輪入口相對氣流角β1不變的情況下，選取出口相對氣流角β2作為設計參數來改變葉輪扭曲規律和幾何尺寸.β1不變保證了葉輪入口氣流角不變，從而不影響導葉的設計.圖6(a)給出了50%葉高處的葉片曲率變化示意圖,從圖6(a)可以看出，隨著β2的增大，透平更接近軸向排氣.圖6(b)給出了葉片扭曲規律變化示意圖.在β2常用范圍(30°～40°)內[14]，選取10種不同的方案進行數值計算，研究動葉輪扭曲規律變化對透平效率的影響，表3給出了不同扭曲規律下葉輪的幾何尺寸，其中方案2表示原葉輪.

由于各種方案的變化相對于原葉輪只是動葉輪發生了改變，導葉柵并未發生改變，故只對動葉輪的變化情況進行分析.在保證邊界條件、網格劃分和求解標準一致的情況下，截取葉輪流道3個截面來分析截面上流動參數和熵增分布隨葉片扭曲變化的分布情況(見圖7).

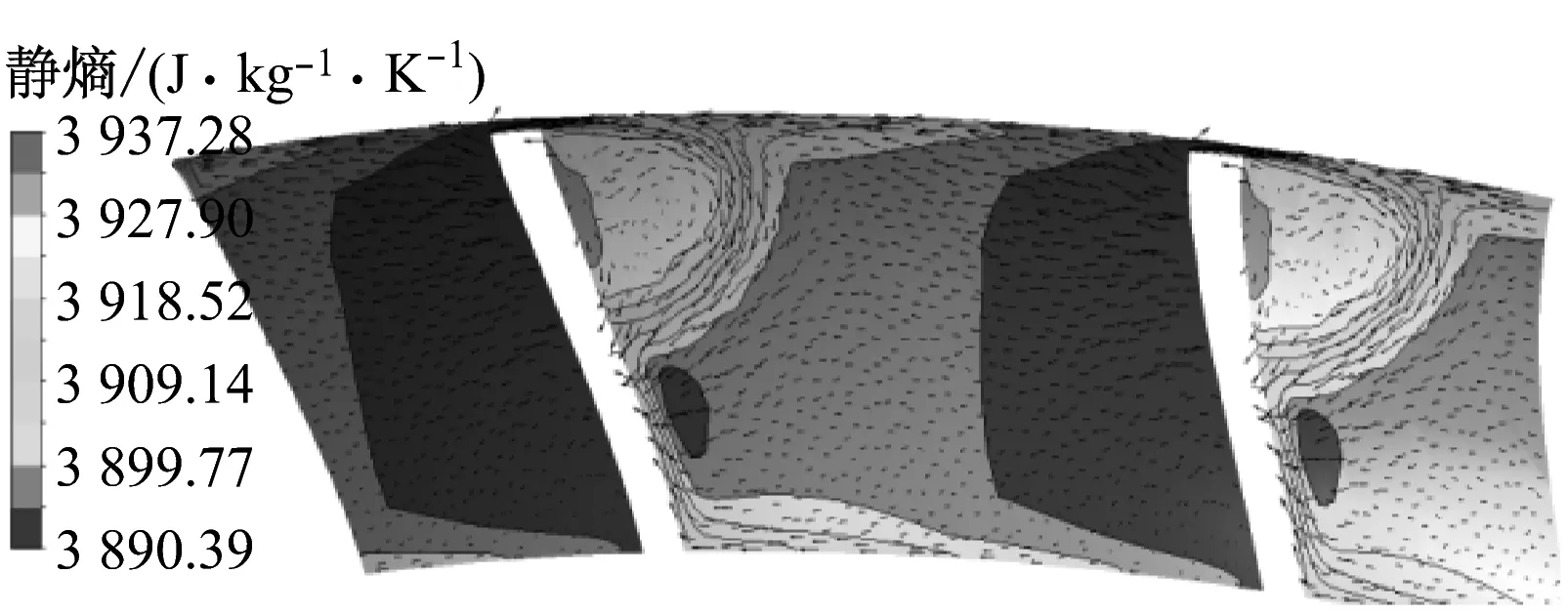
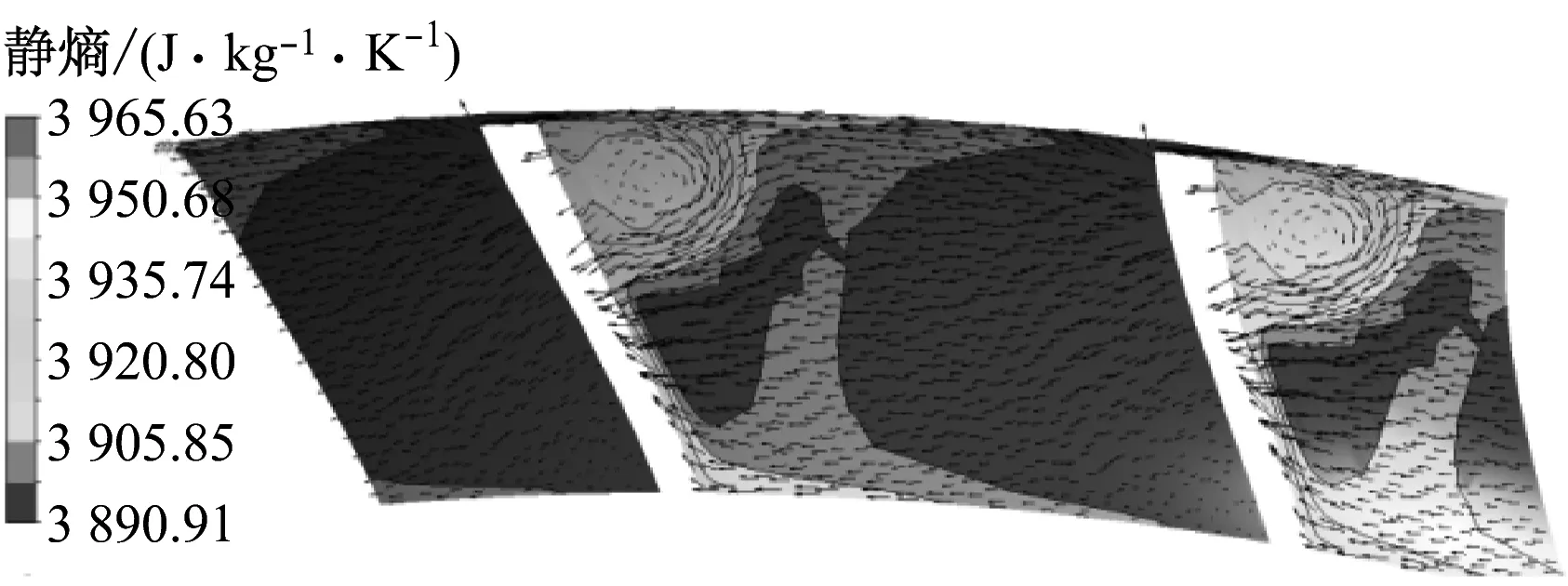
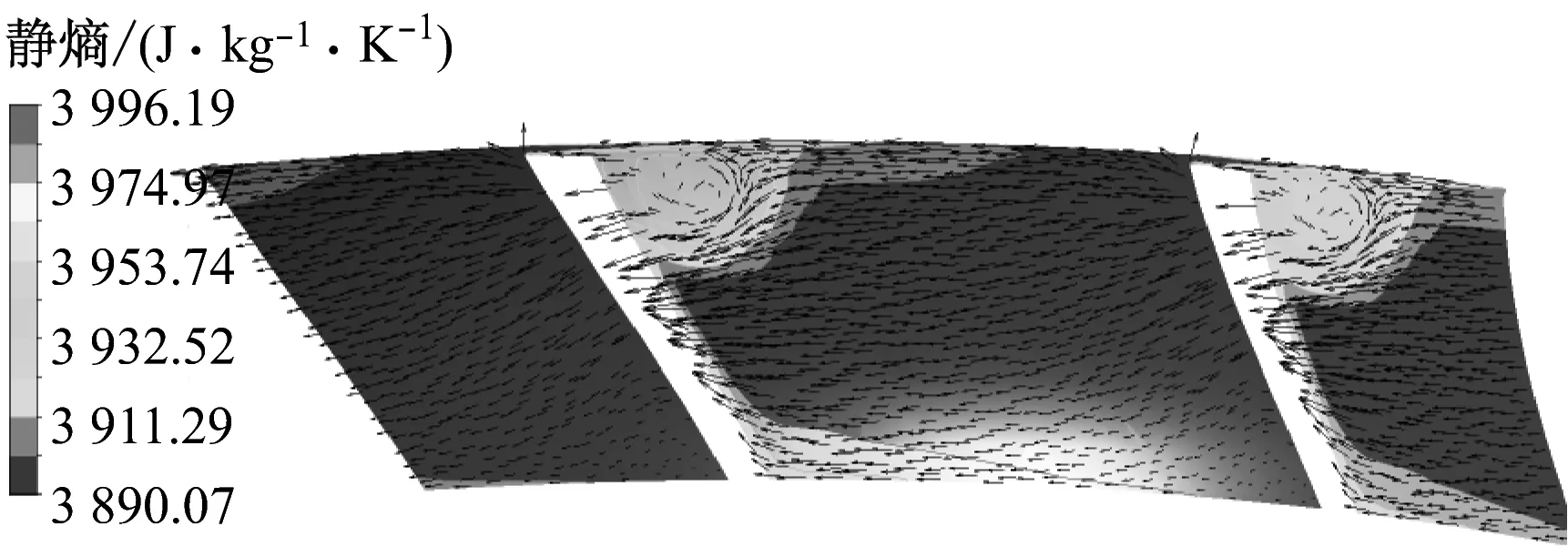
由于篇幅所限，間接選取4種β2對應的扭曲葉片進行研究.圖8給出了截面速度矢量在切向的分量和靜熵分布，每個截面左邊是吸力面，右邊是壓力面.由圖8可知，在截面1，4種β2下的靜熵值都是吸力面明顯高于壓力面，靠近吸力面左上角有明顯的高于其他部位的高熵增區域，且高熵增區域隨著β2的增大有所減小，但其高熵增區域的熵值逐漸增大，即β2越小其熵值分布越均勻.靠近吸力面葉頂處均有明顯的泄漏渦存在，4種β2下都存在氣流從壓力面向吸力面的橫向流動，隨著β2的增大，橫向流動的趨勢也逐漸增強.

氣流從截面1流到截面2，靠近葉頂處的渦流依舊存在，只是渦流的位置有所遠離吸力面.認為靜熵值在3 917 J/(kg·K)以上的區域是流動損失較大的部位，整體上，β2從31°增大到37°，高熵增區域面積以輻射狀向外擴散，呈增大趨勢，相應靜熵的峰值也逐漸增大，β2從31°增大到33°時的增幅最大.雖然β2為33°、35°和37°時高熵增區域面積差別不大，但由于其靜熵值逐漸增大，所以整體熵增也逐漸增大，意味著損失更多，透平性能更差.

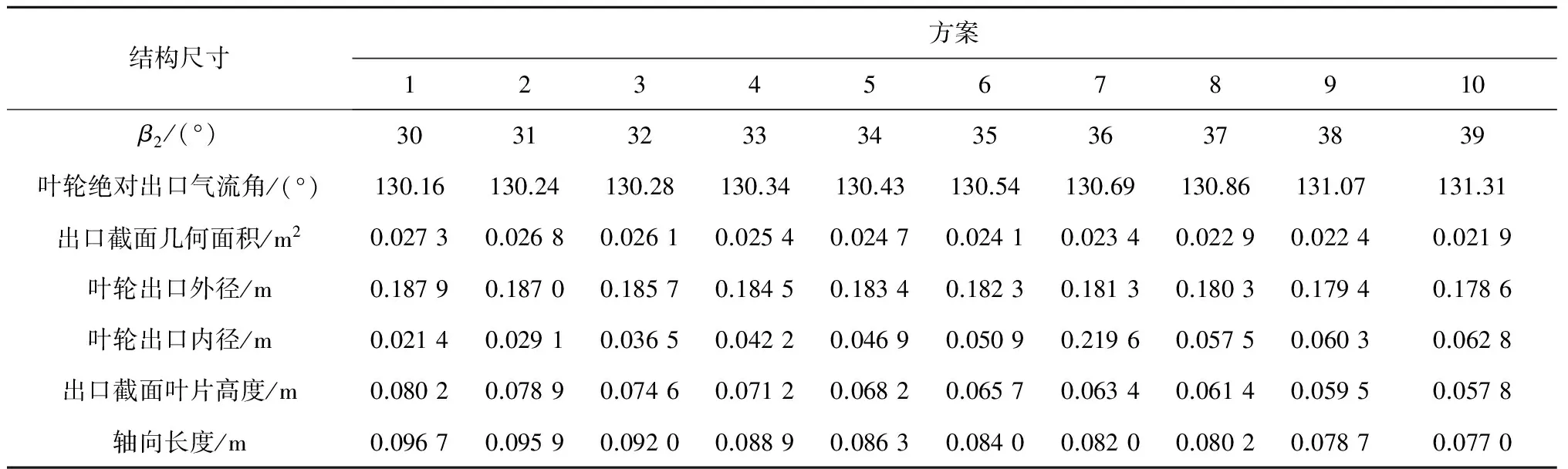
表3 不同扭曲規律下的結構尺寸

圖7 流道截面示意圖

在截面3，一直存在于葉頂處的泄漏渦消失，截面3上的熵增分布與截面2上類似.

圖9給出了4種不同扭曲葉片下葉輪表面的靜壓分布曲線.從圖9可以看出，在壓力面上，基本為順壓梯度流動，大部分載荷集中在前50%流向位置，除β2=31°對應的葉片外，其余3種情況在0.9軸向弦長到出口均有逆壓梯度，在這些區域邊界層增長較快，葉輪的型面損失加大.吸力面上，隨著β2的增大，順壓段長度減小，逆壓梯度段增加.除了β2=31°，其余3種情況下葉片吸力面大多時候都處于逆壓梯度流動，這是由于在0.06～0.15軸向弦長出現了壓力急降，產生了過度膨脹情況.

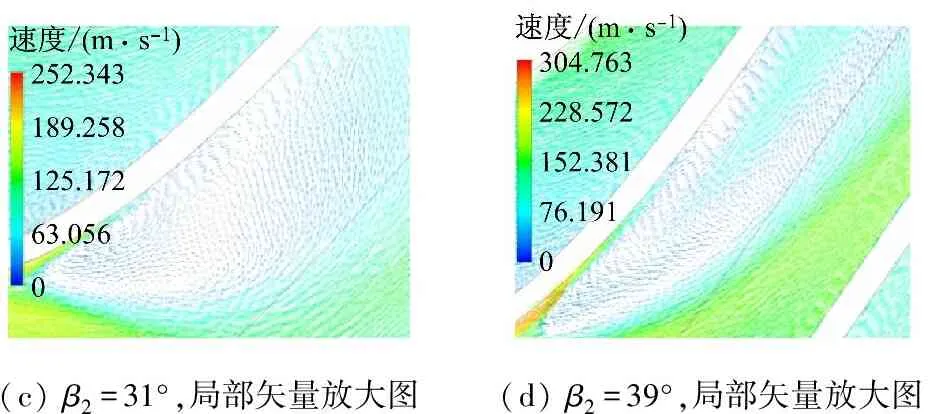
為了進一步分析葉輪扭曲改變引起的葉輪性能變化，選取β2=31°和39°對應的葉輪內部參數進行分析.為了避免葉頂間隙泄漏流影響到流動分離現象的捕捉，選取2種氣流角下85%葉高截面處葉輪內參數分布來進行對比分析(見圖10).從圖10(a)可以看出，β2=31°時壓力沿著流道方向依次降低，主要壓降集中在流道前部，表明工質膨脹做功主要在此區域，整體做功狀況良好，只是在葉片型線轉折處有小范圍低壓區域.相對于β2=31°時的靜壓分布,β2=31°時流道20%處的低壓區范圍明顯增大，逆壓梯度區域向流道中部擴散，氣流經低壓區劇烈加速后減速，氣流不再沿葉片表面流動，從而形成分離區，出現大尺度漩渦.這會擾亂主氣流方向，增大流動阻力，降低整體效率.這與β2=31°和39°時低壓區域的矢量放大圖相對應，與β2=31°相比，β2增大至39°時，低能流體團質量和范圍沿著流向位置增加，影響范圍更廣.

(1)

圖11給出了不同葉輪出口相對氣流角下透平輪周效率的理論變化趨勢與CFD模擬變化情況.由圖11可知，透平效率在β2為30°～40°內變化的最大值約為2.44%，CFD模擬結果變化規律與理論變化趨勢基本保持一致，透平輪周效率均隨β2的增大而降低，并且下降趨勢逐漸增大，這是由于葉輪內部流動惡化導致動葉速度系數下降的緣故.

β2=31°時輪周效率最大，為85.64%，與β2=30°時的輪周效率幾乎相等，β2的減小將不能繼續有效提高輪周效率，只會增加工藝與造型的困難.β2=31°時的葉輪幾何形狀具有更加優越的氣動性能，使葉輪內部的壓降、溫降等分布更加合理，更能夠滿足透平設計的需要.

β2=31°

β2=33°

β2=35°

β2=37°

β2=31°

β2=33°

β2=35°

β2=37°

β2=31°

β2=33°

β2=35°

β2=37°

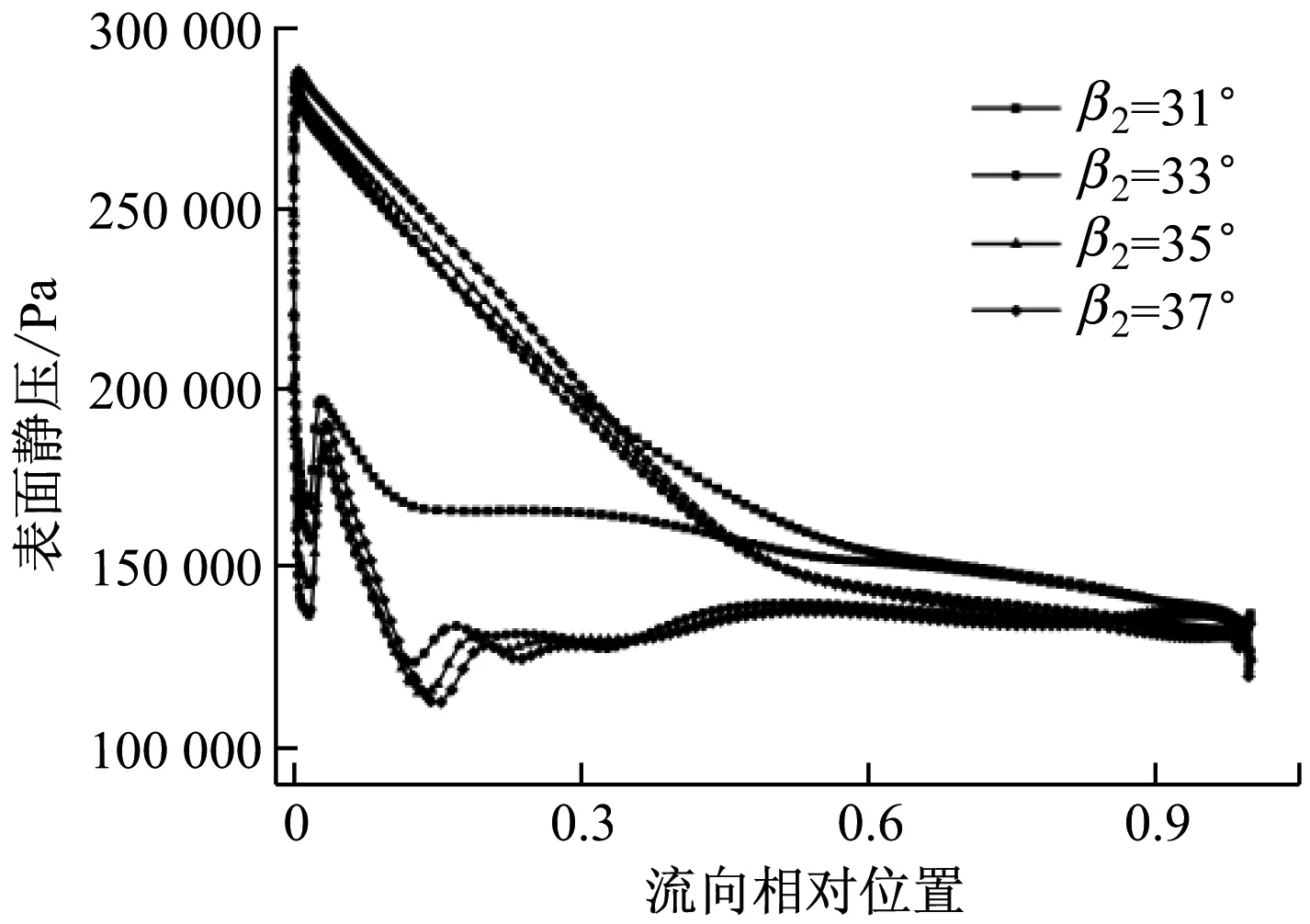
圖9 各向心葉輪表面靜壓分布曲線

3 結 論

(1) 以環己烷為工質設計的向心透平具有良好的氣動性能，并表現出較好的熱力學性能.所設計的向心透平熱力參數與數值模擬結果基本吻合，模擬結果能真實地反映透平內部流動特性.

(2) 在葉輪通道內氣流存在由吸力面向壓力面流動的趨勢，并且在葉輪葉頂部位有較大的流動損失.較小的β2對應的葉輪扭曲形狀能抑制氣流由吸力面向壓力面的流動，但對葉頂渦流的影響不大.

(3) 通過選取β2作為葉輪扭曲規律的指標，進行透平設計造型與模擬驗證，得出透平輪周效率隨著β2(30°～40°)的減小而升高，升高趨勢逐漸減緩的結論.β2=31°時葉輪扭曲形狀氣動性能更加優越，葉輪內部流動更加順暢，壓降和溫降分布更加合理.

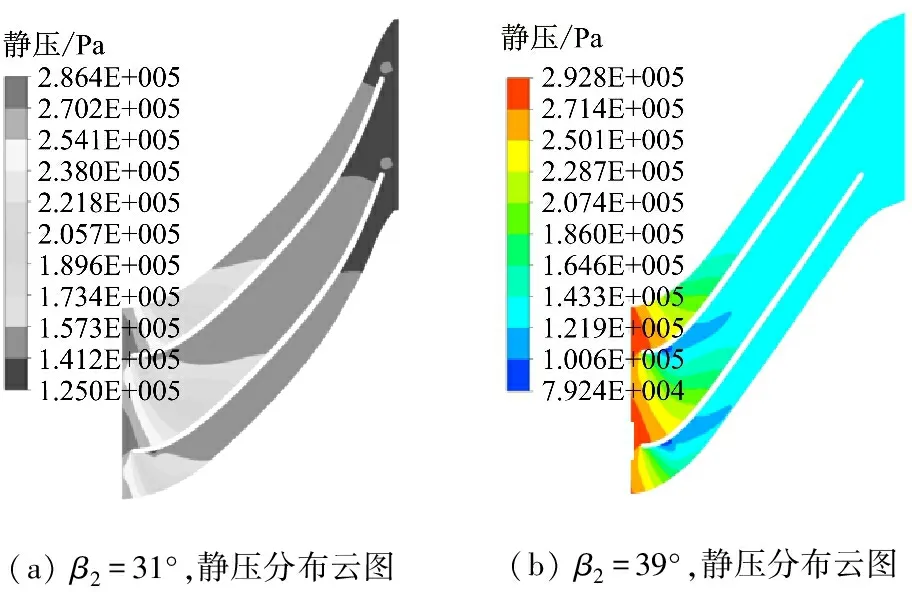
(a)β2=31°，靜壓分布云圖(b)β2=39°，靜壓分布云圖

(c)β2=31°，局部矢量放大圖(d)β2=39°，局部矢量放大圖

圖10 85%葉高處的靜壓分布云圖和局部矢量放大圖

Fig.10 Static pressure distribution at 85% blade height and the partial enlarged detail

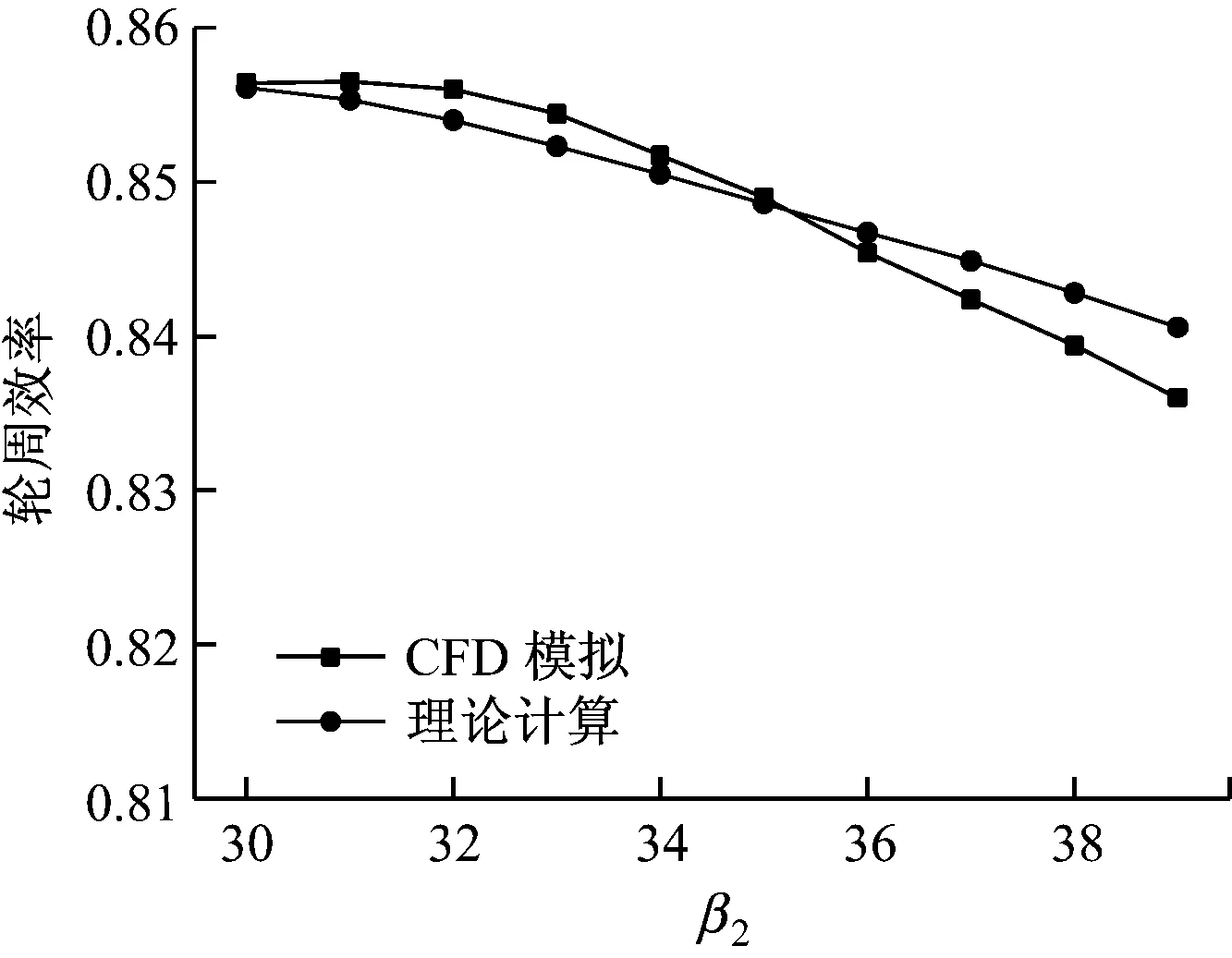
圖11 不同葉輪出口相對氣流角下的透平輪周效率

[1] BADR O, NAIK S, O'CALLAGHAN P W, et al. Expansion machine for a low power-output steam Rankine-cycle engine[J]. Applied Energy, 1991, 39(2): 93-116.

[2] AUNGIER R H. Turbine aerodynamics: axial-flow and radial-inflow turbine design and analysis[M]. New York, USA: ASME Press, 2006.

[3] 王慧, 李水蓮, 魏新利. 向心透平葉輪子午面形狀等腰梯形設計法[J]. 機械科學與技術, 2015, 34(5): 678-682.

WANG Hui, LI Shuilian, WEI Xinli. Isosceles trapezoid design method to develop the meridional profile on impeller[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(5): 678-682.

[4] 邵帥, 鄧清華, 豐鎮平. 向心透平初始設計自動進化尋優方法與變工況性能預測模型[J]. 工程熱物理學報, 2016, 37(1): 67-71.

SHAO Shuai, DENG Qinghua, FENG Zhenping. An automated approach for the radial inflow turbine preliminary design and off-design prediction[J]. Journal of Engineering Thermophysics, 2016, 37(1): 67-71.

[5] 孫冠珂, 李文, 張雪輝, 等. 向心渦輪進氣結構的氣動性能及損失機理[J]. 航空動力學報, 2015, 30(8): 1926-1935.

SUN Guanke, LI Wen, ZHANG Xuehui, et al. Aerodynamic performance and losses mechanism of radial turbine intake components[J]. Journal of Aerospace Power, 2015, 30(8): 1926-1935.

[6] CHEN B, YUAN X. Advanced aerodynamic optimization system for turbomachinery[J]. Journal of Turbomachinery, 2008, 130(2): 021005.

[7] 李艷, 顧春偉. 高膨脹比有機工質向心透平氣動優化研究[J]. 工程熱物理學報, 2013, 34(7):1239-1242.

LI Yan, GU Chunwei. Aerodynamic optimization study for a radial-inflow organic turbine with high expansion ratio[J]. Journal of Engineering Thermophysics, 2013, 34(7):1239-1242.

[8] 謝商育, 王書義. 基于遺傳算法的渦輪增壓器葉輪優化設計[J]. 裝甲兵工程學院學報, 2001, 15(3): 72-76.

XIE Shangyu, WANG Shuyi. Optimal design for the blades of turbocharger by genetic algorithm[J]. Journal of Armored Force Engineering Institute, 2001, 15(3): 72-76.

[9] 岳松, 張奧, 張燕平, 等. 中高溫太陽能有機朗肯循環系統向心透平氣動設計研究[J]. 機械工程學報, 2015, 51(4): 155-160.

YUE Song, ZHANG Ao, ZHANG Yanping, et al. Aerodynamic design study of radial inflow turbine used in middle-high temperature solar organic Rankine cycle system[J]. Journal of Mechanical Engineering, 2015, 51(4): 155-160.

[10] 韓中合, 吳偉銘, 王智. 熱力學模型對ORC透平二維導葉柵流場模擬結果的影響[J]. 動力工程學報, 2014, 34(11): 909-914.

HAN Zhonghe, WU Weiming, WANG Zhi. Influence of thermodynamic model on simulation results of 2D flow field in an ORC turbine nozzle[J]. Journal of Chinese Society of Power Engineering, 2014, 34(11): 909-914.

[11] 韓中合, 杜燕, 王智. 有機朗肯循環低溫余熱回收系統的工質選擇[J]. 化工進展, 2014, 33(9):2279-2285.

HAN Zhonghe, DU Yan, WANG Zhi. Medium selection of organic Rankine cycle (ORC) in low temperature waste heat[J]. Chemical Industry and Engineering Progress, 2014, 33(9):2279-2285.

[12] SAURET E, GU Yuantong. Three-dimensional off-design numerical analysis of an organic Rankine cycle radial-inflow turbine[J]. Applied Energy, 2014, 135: 202-211.

[13] AGRAWAL A, CORNELIO A A, LIMPERICH D. Investigation of cubic EOS models for HFO-1234yf refrigerant used in automotive application[C]//International Refrigeration and Air Conditioning Conference.USA:Purdue University, 2012.

[14] 李燕生, 陸桂林. 向心透平與離心壓氣機[M]. 北京: 機械工業出版社, 1984.

[15] 舒士甄, 朱力, 柯玄齡, 等. 葉輪機械原理[M]. 北京: 清華大學出版社, 1991.

Effects of Impeller Twisting Law on Performance of the ORC Radial Inflow Turbine

WANGZhi,YINLibing

(MOE's Key Lab of Condition Monitoring and Control for Power Plant Equipment, North China Electric Power University, Baoding 071003, Hebei Province, China)

A 200 kW radial inflow turbine was thermodynamically and structurally designed by taking cyclohexane as the working medium, of which the internal flow was numerically studied, so as to analyze the effects of impeller twisting law on the performance of the turbine. Results show that the radial inflow turbine previously designed has good flow characteristics under transonic conditions. The twisting degree may affect the flow path profile of the impeller and the angle between the outlet gas flow and the axial direction. Meanwhile the maximum value of the wheel efficiency change may reach 2.44% under different impeller twisting laws, and the twisting law is an important factor influencing the structural design optimization of the impeller.

radial inflow turbine; impeller twisting law; wheel efficiency; thermodynamic design

2016-06-02

2016-07-25

國家自然科學基金資助項目(51306059)；華北電力大學中央高校基本業務費專項資金資助項目(2014ZD34)

王 智(1978-)，男，河北保定人，副教授，主要從事水蒸氣相變理論、汽輪機內凝結流動及葉輪機械CFD與優化設計方面的研究. 尹立冰(通信作者)，男，碩士研究生，電話(Tel.)：13463297742；E-mail：13463297742@163.com.

1674-7607(2017)05-0367-06

TK14

A 學科分類號：470.30