基于改進粒子群算法的橫動伺服控制系統辨識*

曹 薇， 羅業才

(1. 廣東水利電力職業技術學院 自動化工程系，廣東 廣州 510925； 2. 華南理工大學 機械與汽車工程學院，廣東 廣州 510640)

基于改進粒子群算法的橫動伺服控制系統辨識*

曹 薇1， 羅業才2

(1. 廣東水利電力職業技術學院 自動化工程系，廣東 廣州 510925； 2. 華南理工大學 機械與汽車工程學院，廣東 廣州 510640)

針對橫動伺服控制系統的黑箱模型，提出了一種基于改進粒子群算法的辨識方法。首先，建立了系統的五階傳遞函數模型，其次，在粒子群算法的基礎上，引入非線性凹函數作為慣性權重的調整策略，從而避免了算法在尋優過程中陷入局部最優，實現了系統模型的優化。最后，為了驗證辨識模型的正確性，進行仿真與實測對比試驗。試驗結果表明：該算法辨識出的模型準確度較高，具有較好的控制品質，對于同一速度輸入信號，仿真與實測的輸出曲線跟隨性好，誤差在-0.5～0.2 rad范圍內，誤差小。

橫動伺服控制系統；粒子群算法；黑箱模型；辨識

0 引 言

橫動伺服控制系統是包覆紗機的核心組成部分[1]，主要由橫動伺服電機、驅動器、嵌入式控制器及PC端組成，通過橫動伺服電機驅動鋼絲輪正反轉帶動導紗器來回擺動，實現紗線高速精密卷繞。橫動伺服控制系統模型的精確性決定了系統的穩定性和可靠性[2-3]，也直接關系到包覆紗機工作效率及工作質量。系統辨識是常用的系統建模方法，通過把系統模型當作未知的黑箱模型，對黑箱模型輸入已知信號，測出其輸出信號，再利用系統參數估計算法來辨識出系統結構和參數[4-5]。常用的系統參數估計算法可以分為兩類：傳統算法和智能算法。傳統算法主要有最小二乘法[6]等，傳統算法是早期的參數估計方法，原理較簡單，但不適用于比較復雜的系統。智能算法主要有遺傳算法[7]、粒子群算法[8]及神經網絡算法[9]等，這些算法一方面很好地彌補了傳統算法的不足，另一方面還能夠實現全局優化，特別是粒子群算法相對于其他算法來說，由于其粒子搜索趨同性使得其搜索能力更強，收斂速度更快。但是，也容易出現“早熟”，陷入局部最優[10-12]。

為此，本文為了辨識某紡紗機的橫動伺服控制系統，提出一種改進粒子群算法來進行系統結構和參數估計，并通過仿真與實測對比試驗來驗證模型辨識的正確性。

1 橫動伺服控制系統數學建模

橫動伺服控制系統主要由伺服電機、鋼絲輪、鋼絲繩、導絲輪、導紗器和卷筒等組成，通過控制伺服電機正反轉帶動鋼絲輪正反轉，通過鋼絲繩傳力帶動導紗器來回擺動。橫動伺服控制系統模型如圖1所示。

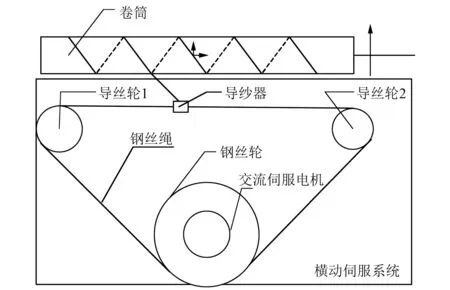
圖1 橫動伺服控制系統

橫動伺服控制系統以PID控制為基礎，系統輸入為電機角速度，輸出為電機角位移，通過三閉環反饋實現高速、高精度控制，如圖2所示，從外到內分別為位置環、速度環及電流環。最外環位置環由輸入位置信號和反饋位置信號形成閉環控制，位置控制器PD將位置環差分信號作為速度環的輸入；中間環速度環由輸入速度信號和反饋電機軸轉速信號形成閉環控制，速度控制器PI將速度環差分信號作為電流環的輸入；最內環電流環由輸入電流信號和反饋電機定子電流信號形成閉環控制。

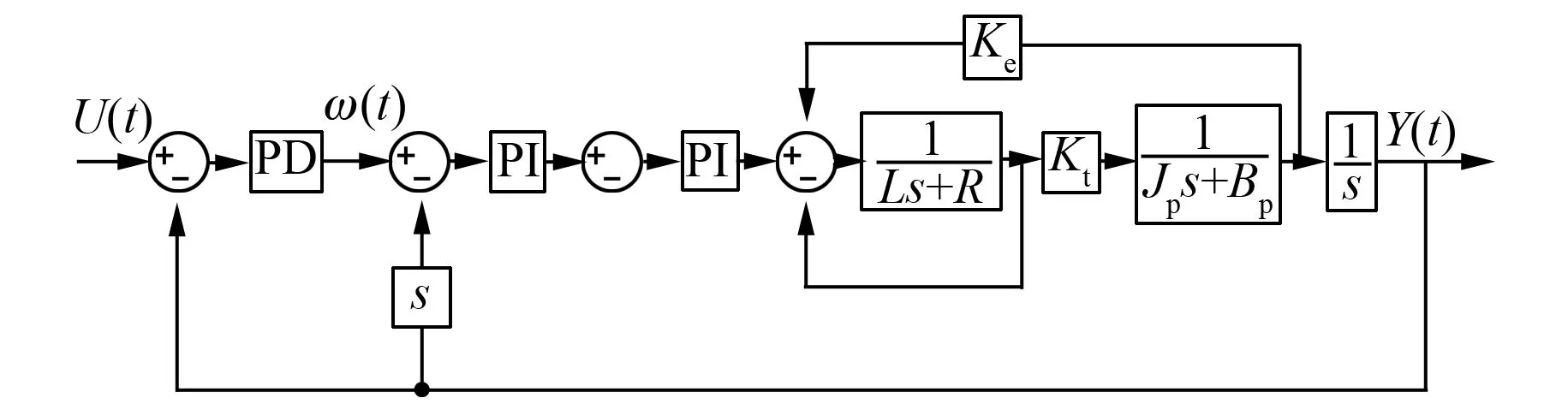
圖2 橫動伺服控制系統控制系統框圖

圖2所示系統模型，其傳遞函數通式為

(1)

式中:a0,a1,a2,b0,b1,b2,b3,b4——橫動伺服控制系統待求取參數。

2 改進粒子群算法

橫動伺服控制系統辨識就是求取系統傳遞函數a0,a1,a2,b0,b1,b2,b3,b4這8個未知參數。本文在粒子群算法的基礎上，引入非線性凹函數作為慣性權重的調整策略，慣性權值的設置是為了影響粒子的局部搜索能力與全局搜索能力的均衡。主要表示上一代的速度對這一代的速度產生的影響。慣性權值越大，那么表示上一代的速度對當前影響越大，粒子將很大程度的沿著自身上一代的速度移動；如果慣性權值很小，那么表明粒子受上一代的影響很小，粒子將很大程度的沿著自身學習的速度移動。慣性權重大，全局搜索能力增強，局部搜索能力下降；反之，慣性權重降低，全局搜索能力下降，局部搜索能力增強。所以，通過動態調整慣性權重來提高算法性能，一方面提高算法的全局搜索能力，避免陷入局部最優，另一方面減小算法迭代次數，節約辨識時間。

改進粒子群算法表達式如下。

(1) 速度更新公式：

(2)

(2) 位置更新公式:

(3)

(3) 引入非線性凹函數作為慣性權重ω(i)的調整策略:

(4)

式中：k——當前迭代代數;ω——慣性權重；c1、c2——加速因子；r1、r2——0到1的隨機數，用來保證群體的多樣性；

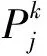
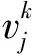
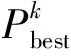
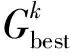
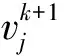
(4) 定義適應度函數。選用誤差平方和的倒數作為改進粒子群算法的適應度函數。適應度函數決定了辨識模型與實際模型的相似度，適應度函數值最大時，采樣點誤差最小，此時辨識參數取得最優值。改進粒子群算法的適應度函數表達

(5)

式中：D——常數(D>0)；Ei——第i次采樣點的誤差；θp(i)——在第i次采樣時的實際位移值；θ(i)——第i次采樣時利用差分方程求出的結果。

(5) 改進粒子算法運行流程圖。改進粒子群算法的運行流程如圖3所示。首先，設置最大的速度區間，防止超出最大的區間，位置信息即為整個搜索空間，在速度區間和搜索空間上隨機初始化速度和位置，設置群體規模size。對模型參數進行尋優，每個粒子都會記住自己飛行過的最佳位置，同時，所有粒子將各自的最優位置進行共享，建立個體最優位置數據庫，那么在這個數據庫里必然有一個最最優位置。所有的粒子將按照式(2)和式(3)分別更新位置和速度，所有的粒子將朝著這個最優目標位置飛去。最后，利用適應度函數進行辨識模型和實際模型相似度計算，先檢查新粒子適應度是否高于原最優適應度；如果高于則對自己的位置和適應度進行更新，再判斷此粒子適應度是否高于全局最優粒子；如果高于則更新全局最優粒子適應度和位置。依此流程進行不斷循環迭代，迭代終止條件如下：(1)算法迭代代數達到設定值；(2)相鄰兩代之間的偏差在一個指定的范圍內即停止，達到終止條件，算法結束，輸出最優值。

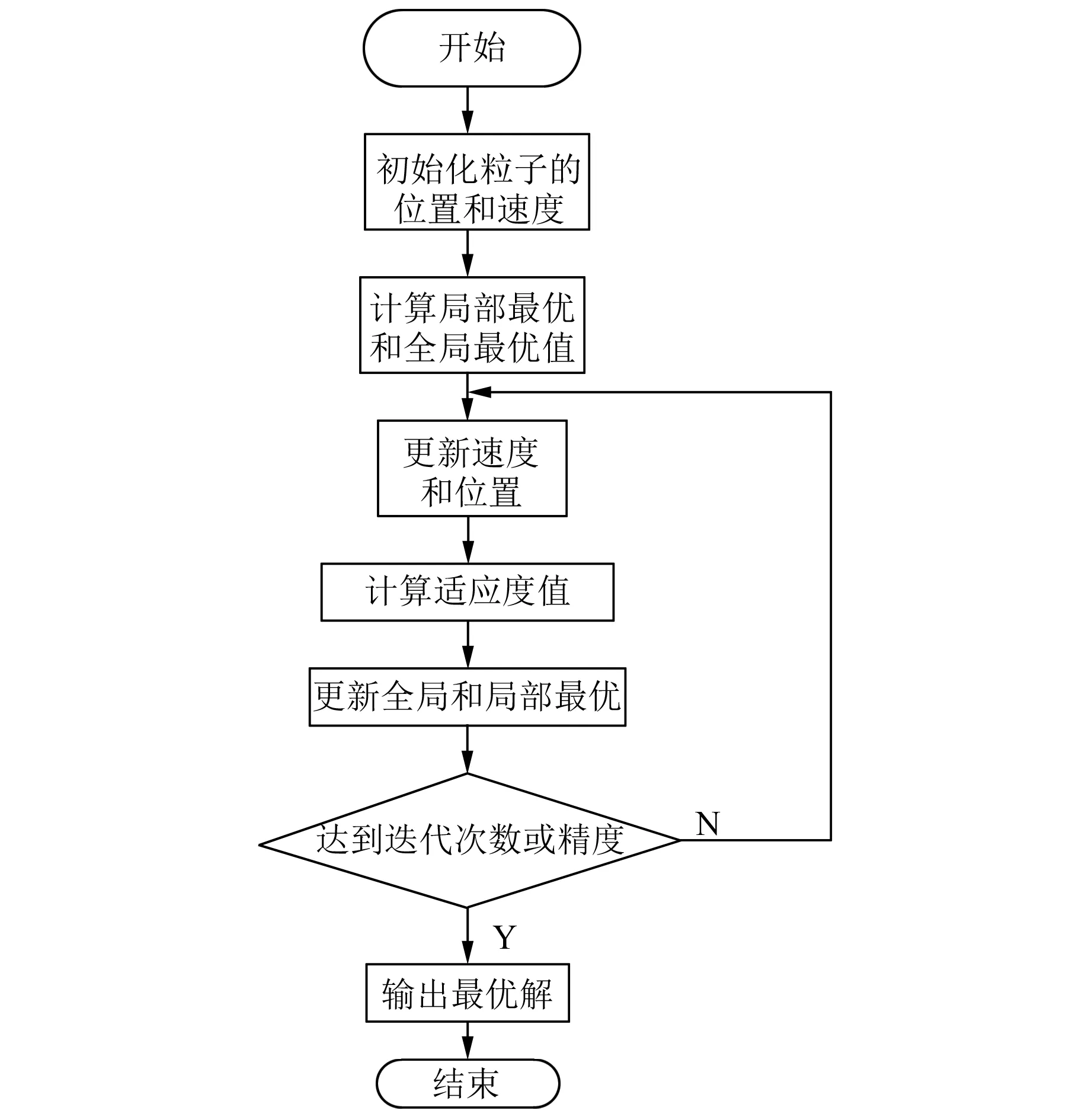
圖3 粒子群智能算法流程圖

3 系統辨識與試驗驗證

本文針對如圖1所示的橫動伺服控制系統，利用改進粒子群算法求取其傳遞函數式(1)中的a0,a1,a2,b0,b1,b2,b3,b4，設置算法初始參數，設置如表1所示。

表1 改進粒子群算法初始參數設置

粒子群適應度值-進化代數曲線如圖4所示。算法在約40代開始收斂，適應度函數取得最大值Fmax=0.074，采樣點誤差最小。此時，辨識參數取得最優值，如表2所示。

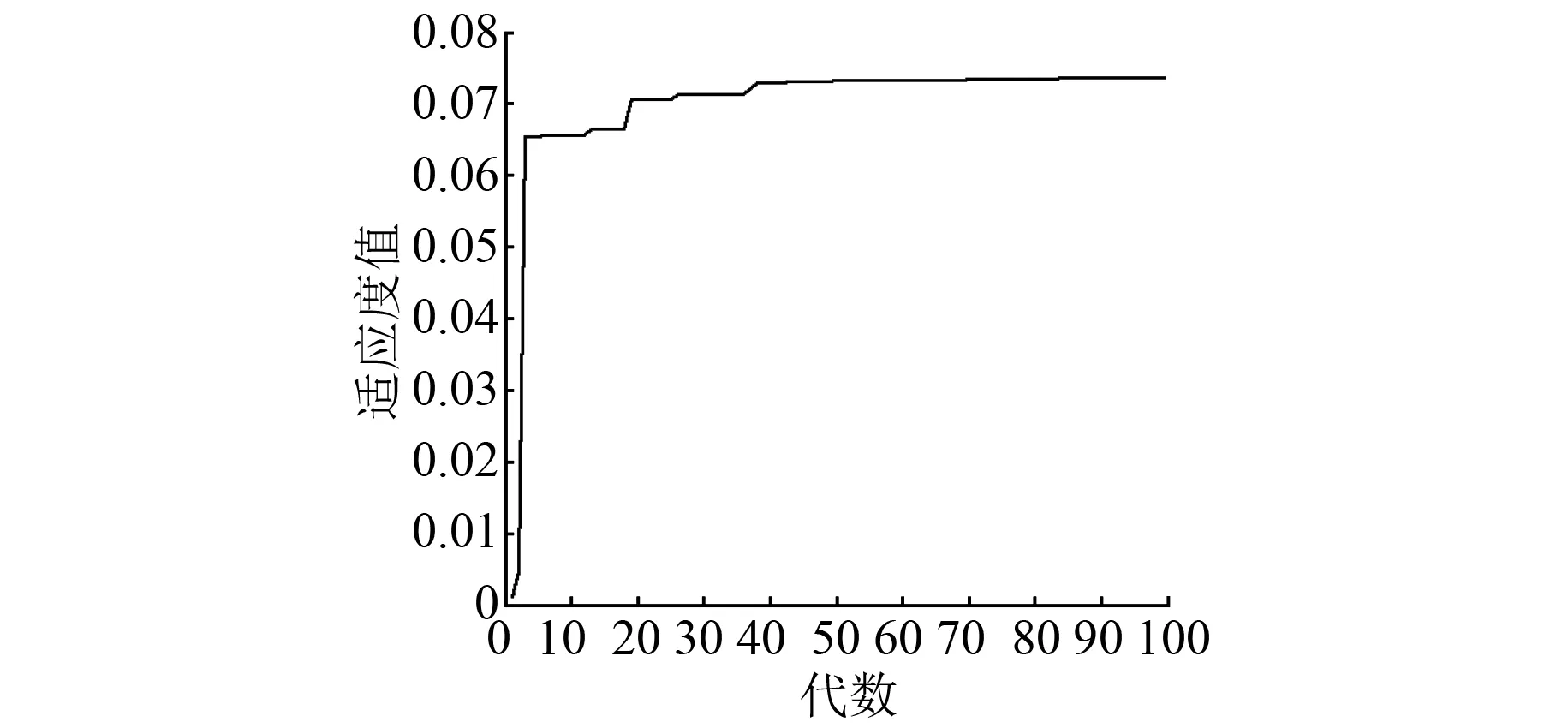
圖4 粒子群適應度值-進化代數曲線

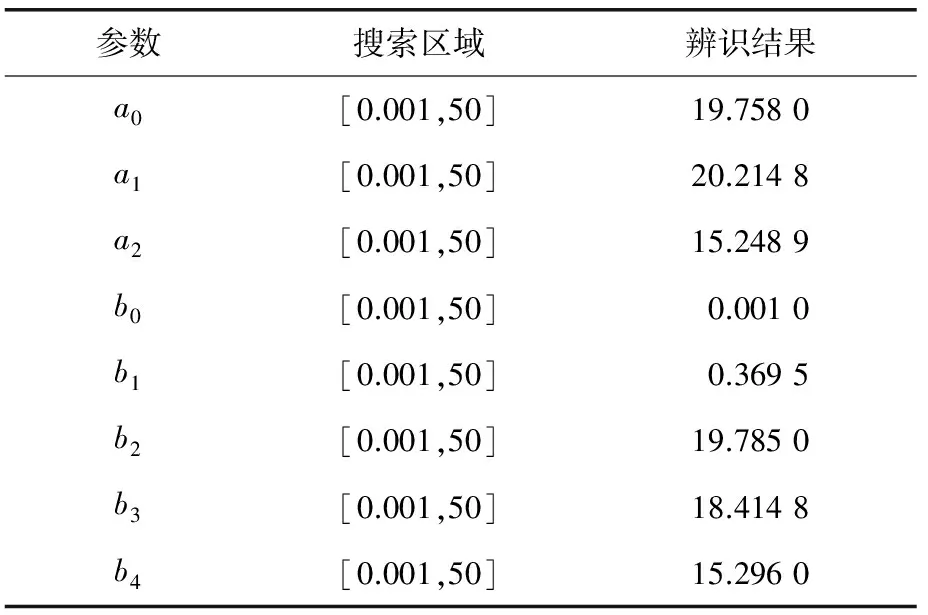
參數搜索區域辨識結果a0[0．001，50]19．7580a1[0．001，50]20．2148a2[0．001，50]15．2489b0[0．001，50]0．0010b1[0．001，50]0．3695b2[0．001，50]19．7850b3[0．001，50]18．4148b4[0．001，50]15．2960

將求取參數代入式(1)，得到橫動伺服控制系統的模型為

(6)

試驗平臺如圖5所示，主要由橫動電機及其驅動器、嵌入式控制器及PC端組成，控制器與伺服電機通過工業以太網EtherCAT總線通信，利用控制器NCTOPLC實時讀取系統電機的轉角，可以得到其輸出曲線及誤差曲線。

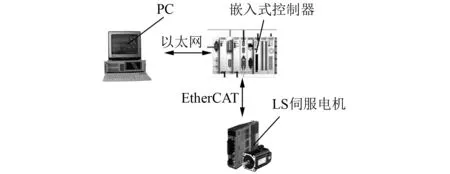
圖5 辨識試驗平臺

為了驗證模型辨識的正確性，輸入同一速度信號v(t)=53.25sin(4πt)，進行仿真與實測對比試驗。試驗結果如圖6、圖7所示。

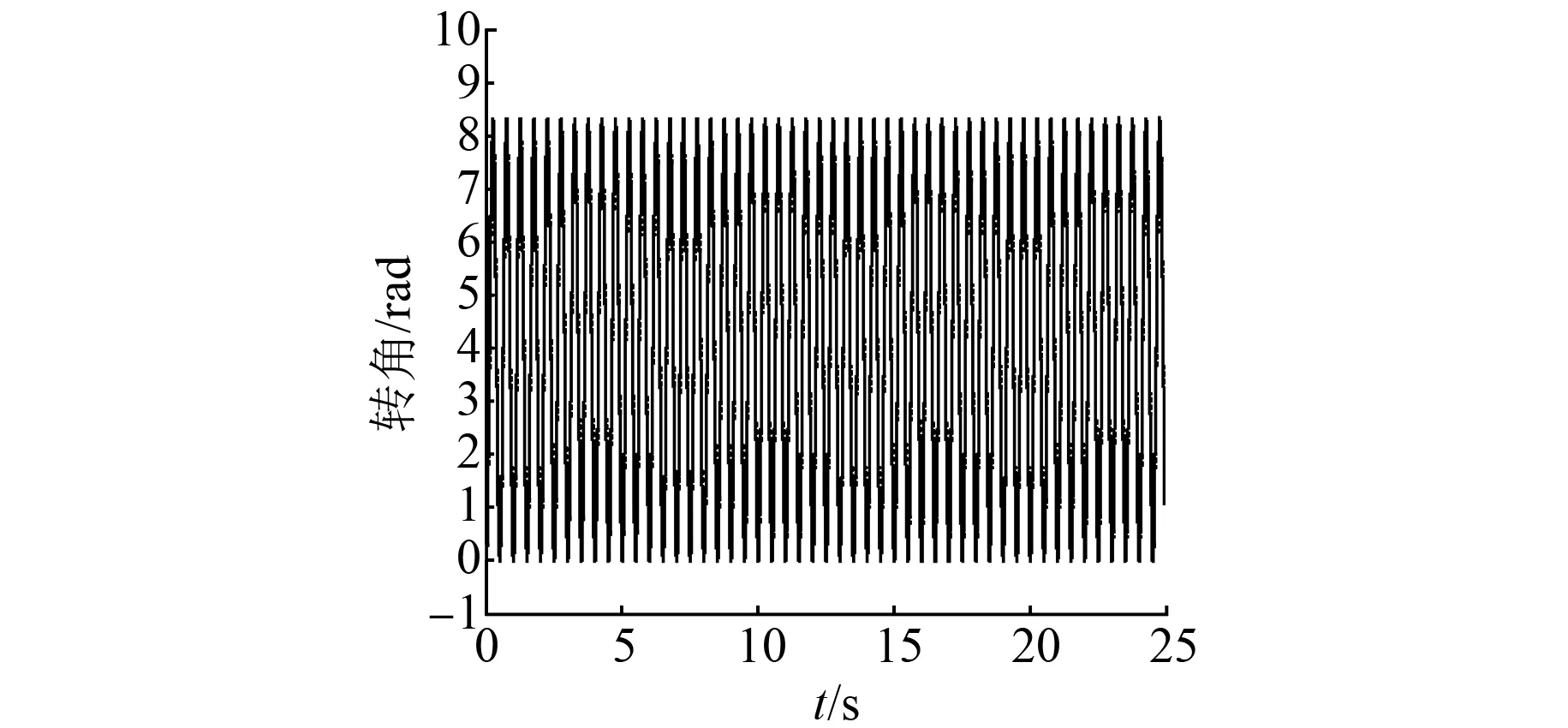
圖6 仿真與實測轉角輸出曲線

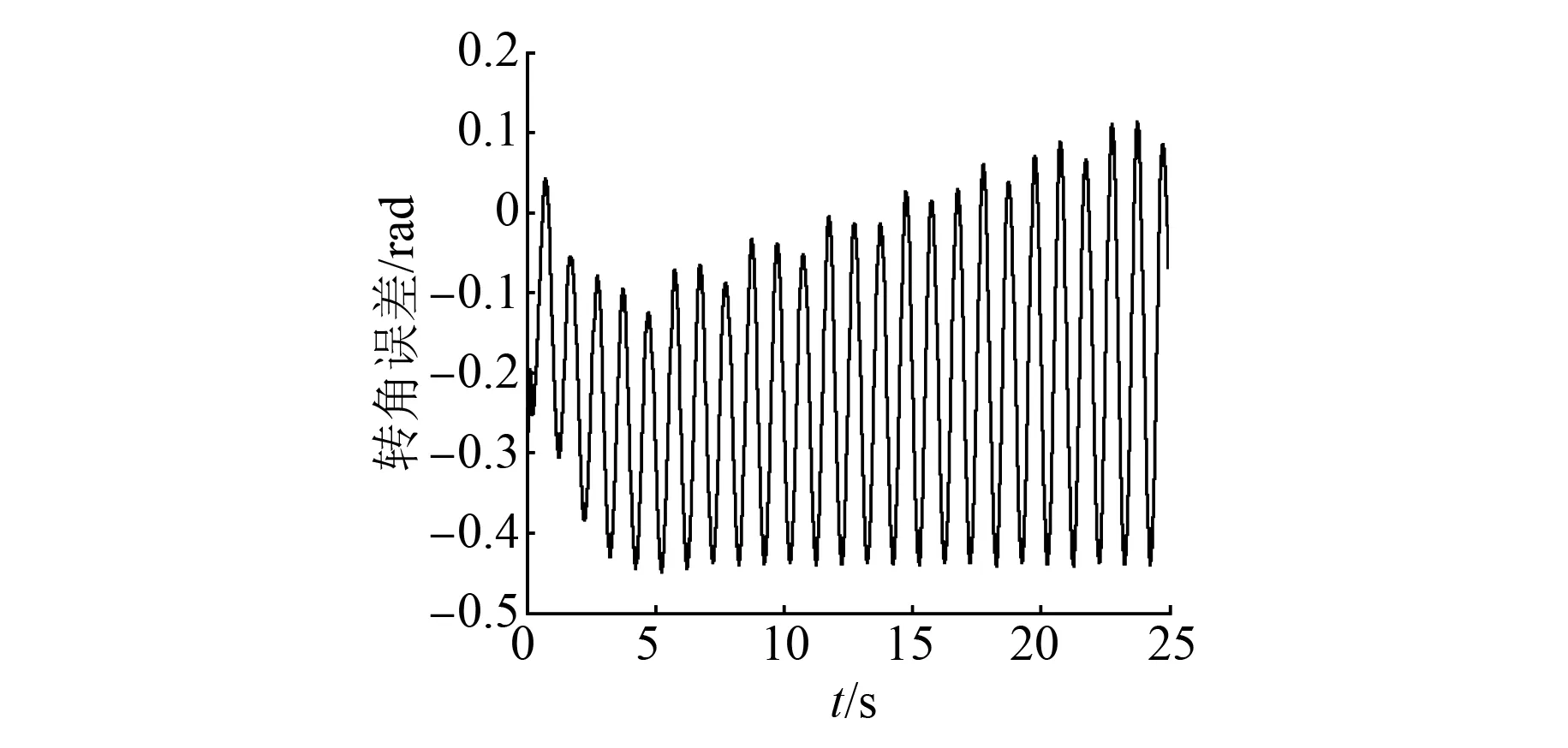
圖7 仿真與實測轉角輸出誤差曲線

由圖6、圖7可知，對于同一輸入信號，仿真與實測輸出曲線的跟隨性好，誤差在-0.5～0.2rad范圍內，誤差小。從而可驗證改進粒子群算法辨識出的橫動伺服控制系統模型準確度較高，具有較好的控制品質。辨識誤差的存在也使系統多了不穩定因素，究其原因，主要是因為實際輸入信號中夾雜了干擾信號。

4 結 語

(1) 針對精密卷繞系統中的橫動伺服控制系統，建立了其五階傳遞函數模型，并設計了一種改進粒子群算法來對該系統的未知參數進行辨識，避免了算法在尋優過程中陷入局部最優，實現了系統模型的優化。

(2) 為了驗證辨識模型的正確性，進行仿真與實測對比試驗。試驗結果表明：該算法辨識出的模型準確度較高，具有較好的控制品質，對于同一速度輸入信號，仿真與實測的輸出曲線跟隨性好，誤差在-0.5～0.2rad范圍內，誤差小。

[1] 馬秀鳳,張玉清,邢明杰.包覆紡紗技術的現狀及發展趨勢[J].紡紗導報,2005(10): 141-142.

[2] 王紹斌,孫衛國,王文郁.絡筒張力和速度對紗線質量的影響[J].棉紡織技術,2002,30(7): 35-37.

[3] 周云端.專用纏繞機的開發與張力控制系統研究[D].西安: 西北工業大學,2006.

[4] 任貴杰,李平康,趙志剛,等.基于改進遺傳算法的單元機組非線性模型參數辨識[J].北京交通大學學報,2011,35(6): 93-97.

[5] 劉勝,宋佳,李高云.PSO并行優化LSSVR非線性黑箱模型辨識[J].智能系統學報,2010,5(1): 51-56.

[6] 李銀國,湯卓群,黃鐳.非持續激勵條件下系統辨識遞推最小二乘最小范數算法[J].控制理論與應用,2009,26(4): 365-370.

[7] 肖曦,許青松,王雅婷,等.基于遺傳算法的內埋式永磁同步電機參數辨識方法[J].電工技術學報,2014,29(3): 21-26.

[8] 程善美,張益.基于協同粒子群算法的PMSM在線參數辨識[J].電氣傳動,2012,42(11): 3-6.

[9] 于開平,牟曉明.基于前向神經網絡的非線性時變系統辨識的改進遞推最小二乘算法[J].振動與沖擊,2009,28(6): 107-110.

[10] 劉朝華,章兢,李小花,等.免疫協同微粒群進化算法的永磁同步電機多參數辨識模型方法[J].自動化學報,2012,38(10): 1698-1708.

[11] 靳其兵,張建,權玲,等.基于混合PSO-SQP算法同時實現多變量的結構和參數辨識[J].控制與決策,2011,26(9): 1373-1377.

[12] 趙洋,韋莉,張逸成,等.基于粒子群優化的超級電容器模型結構與參數辨識[J].中國電機工程學報,2012,32(15): 155-161.

Identification of Horizontal Dynamic Servo Control System Based on Improved Particle Swarm Optimization Algorithm*

CAOWei1,LUOYecai2

(1. Department of Automation Engineering, Guangdong Technical College of Water Resource and Electric Engineering, Guangzhou 510925, China; 2. School of Mechanical &Automotive Engineering, South China University of Technology, Guangzhou 510640, China)

In view of the black box model traverse servo control system, an identification method based on improved particle swarm optimization algorithm was proposed. First, the establishment of a system of fifth order transfer function model. Secondly, based on the particle swarm optimization algorithm, the introduction of a nonlinear concave function as a strategy of inertia weight adjustment, so as to avoid the algorithm in search of falling into the local optimum in the process of optimization, the optimization of the system model. Finally, in order to validate the identification model was correct, comparing simulation and actual measurement experiment. The experimental results showed that: the algorithm model was accurate and reliable, with good control quality, for the same speed input signal, simulation and measurement of the output curve tracking was good, the error in the -0.5～0.2 rad range, the error small.

traverse servo control system; particle swarm algorithm; black box model; identification

國家重點研發計劃項目(2016YFC0104901)；廣東水利電力職業技術學院創新強校工程自主創新能力提升類項目(050117)；2014年廣東省特色創新項目(自然科學類)(2014KTSCX146)

曹 薇(1973—)，女，副教授，研究方向為機電一體化。

TM 301.2

A

1673-6540(2017)04- 0043- 04

2016 -09 -20