薄板船體結構焊接失穩變形的數值分析進展

王江超

(華中科技大學 船舶與海洋工程學院， 湖北 武漢 430074)

?

薄板船體結構焊接失穩變形的數值分析進展

王江超

(華中科技大學 船舶與海洋工程學院， 湖北 武漢 430074)

回顧總結數值分析在角接焊接頭以及船體典型焊接結構失穩變形研究中的應用，主要闡述薄板焊接失穩變形的復雜多樣性以及焊接失穩變形的形成機理。著重介紹研究失穩現象的數學理論基礎。概述當前使用熱彈塑性有限元法、彈性有限元法和特征值法等數值分析方法研究焊接失穩變形的現狀及進展。

薄板船體結構；焊接失穩；數值分析；大變形理論；特征值分析

0 引言

采用高強鋼薄板設計來減輕船體結構自身重量是解決當前船舶運營所面臨的降低能耗、減少排放、保護環境以及提高運載量等問題的一種有效措施。目前，結構輕量已成為高新船舶及海洋開發裝備生產中一種應用極為廣泛的先進制造技術。高強鋼薄板可在實現輕量化的同時，完全滿足船舶及海洋結構物的強度要求。但薄板結構因板材厚度減少其保持穩定性的能力顯著降低，因此，在焊接制造過程中，薄板船體結構會因焊縫處產生的縱向收縮力而發生失穩并導致產生失穩變形，從而大幅降低建造精度。

焊接失穩變形是一種不同于常見焊接變形的變形模式，通常會呈現出多種不同形式的面外變形分布[1]。它會大幅降低薄板船體結構的制造尺寸精度。同時，因其不穩定的特性，在后期的矯正過程中，不僅增加制造成本、延長工時，而且很難完全消除[2]。因此，須通過計算并預測出產生焊接失穩變形的臨界條件，改變并控制實際的焊接制造過程，以得到盡可能小的引起焊接失穩的驅動力，避免其接近失穩臨界條件，從而預防焊接失穩變形的發生，保證建造精度。

當前，對薄板結構焊接失穩變形的研究主要集中在使用數值分析的方法再現失穩現象，并預測焊接失穩變形的分布趨勢及失穩模態。同時，分析影響焊接失穩變形產生的各個因素，解釋其產生機理，也是重要的研究內容之一。

1 典型船體結構焊接失穩變形及特征

薄板船體結構，常常使用角焊完成筋板與底板的連接，以增加其剛度和穩定性。一般而言，T型接頭及其焊接結構在焊縫收縮的作用下失去穩定性，將會表現出多種與初始狀態完全不同的結構形態。因此，焊接失穩變形不同于其他焊接變形類型，它沒有簡明的變形形式，很難判斷。

船體結構受結構自身設計及剛度的影響，焊接失穩變形是一種局部波浪式或整體扭轉式變形，且變形量相對較大[1]。在簡單的薄板堆焊以及對接接頭中，焊接失穩變形呈現出“馬鞍形(Saddle)”的模態[3]。對于T型角焊接頭，焊接失穩變形則可能以多種形式呈現(見圖1)，包括產生整體的“扭轉(Twist)”變形以及形式更加復雜的復合失穩變形模式。橫豎交錯的船體加筋板焊接結構，也可能因其結構設計、尺寸材質以及焊接過程不同而產生完全不同模態的焊接失穩變形[4- 5]，如圖2所示。

圖1 船體T型角焊接頭可能產生的焊接失穩變形模態

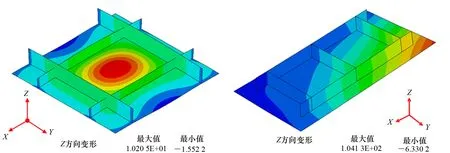
圖2 船體加筋板焊接結構中產生的復雜焊接失穩變形

在船體結構中，焊接產生的面外變形主要由面外彎曲角變形和失穩變形共同決定。在中厚板及厚板結構中，由于失穩變形沒有發生，面外變形僅由面外彎曲角變形引起，底板會呈現出“瘦馬(Hungry Horse)”形態的面外變形。失穩變形產生之后，如圖3所示，焊接結構表現出來的特征有：

(1) 底板多處產生凹凸不平的波浪式變形；

(2) 底板面外產生很大量級的變形。

然而，當焊接產生的面外彎曲角變形太大時，其對面外變形的貢獻會掩蓋焊接失穩現象，使得焊接失穩的特征表現得不夠明顯[2]。當然，面外變形也受到焊縫收縮力產生的彎曲力矩的影響。當焊接結構橫斷面的質心位置與其受力點的位置(焊縫)不相同時，就會產生一定的彎曲力矩，從而可能導致產生面外變形。

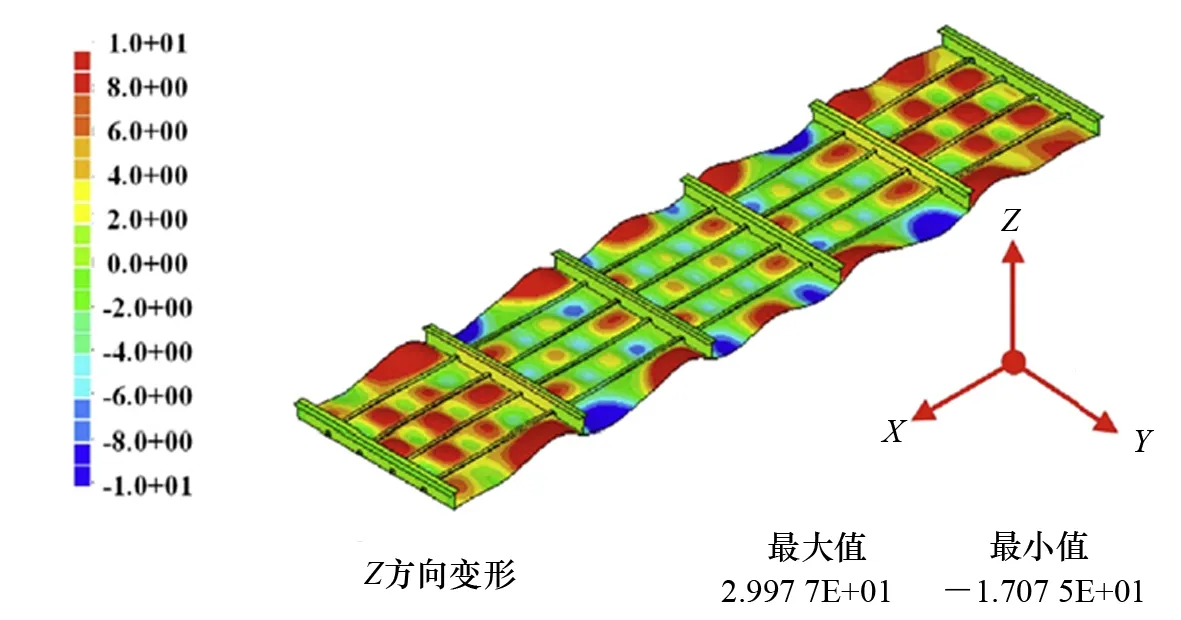
圖3 船體加筋板失穩后的面外變形分布模態

對于使用超高強鋼薄板的船體結構，由于材料屈服強度的明顯提升，結構在焊接加熱過程中，加熱焊縫對周圍母材產生擠壓作用，可能會導致船體結構在屈服之前發生焊接瞬態熱失穩現象[6]。

因此，焊接失穩變形是一種現象復雜且呈現多變模態的變形類型。特別是在大型且復雜的船體焊接結構中，其表現形式將更加多樣化，相關的機理分析和計算分析預測也都非常困難，從而很難保障船舶建造精度。

2 薄板焊接失穩產生機理

焊接失穩變形的本質是焊接接頭或者焊接結構在焊縫收縮力的作用下，失去穩定性而發生的形狀變化。雖然焊接失穩變形的形式多種多樣，其產生的根本原因均在于收縮力對結構的壓縮作用。

日本大阪大學的上田幸雄教授及其團隊成員，專注于船體結構的精度建造研究，經過試驗測量觀察、理論分析以及大量有限元數值計算得出：固有應變(去除彈性應變之外的所有應變分量)是產生焊接變形和殘余應力的根源。如果將橫斷面上的所有固有應變乘以彈性模量，再乘以其存在的面積，則固有應變轉化為橫斷面的固有作用力；而當作用力的作用點與橫斷面的質心不重合時，將產生彎曲力矩；以及由應變的定義(單位長度的變形量)可求取橫向變形；這樣綜合之后就得到了焊接產生的固有變形。

(1)

(2)

(3)

基于上述固有變形理論的研究[7]發現：對于多層多道焊或者平行焊縫的薄板船體結構，焊接失穩變形僅由縱向收縮力決定；面外橫向彎曲(角變形)和縱向彎曲(通常因數值相對較小而忽略不予考慮)以及初始擾度不會決定焊接失穩變形是否發生，但作為一種擾動，在失穩條件滿足時，會促發焊接失穩現象發生；橫向位移在此對失穩沒有任何影響。當然，在沒有任何擾動的情況下，即使焊接產生的縱向收縮力大于失穩產生的壓縮力，焊接失穩變形也不會產生。在相互垂直的船體加筋板焊接結構中，橫向位移在垂向加強筋的約束下不能隨意移動時，面內固有收縮(縱向收縮力和橫向位移)將共同決定焊接結構是否發生失穩現象；焊接產生的面外橫向/縱向彎曲以及初始擾度，依然只會在結構滿足失穩條件時，促使結構失去穩定性，產生失穩變形。

還有部分船舶建造領域的學者[8-9]認為：薄板船體結構焊接失穩變形產生的驅動力是縱向壓縮殘余應力。其中，典型的橫斷面焊接殘余應力分布是：焊縫處的殘余應力為拉應力，在沒有加工硬化時，其數值等于材料的屈服應力；遠離焊縫的區域是壓應力，且最終在邊界區域趨近于零。遠離焊縫處的縱向壓縮殘余應力也稱之為施加的焊接載荷(Applied Weld Load， AWL)，當其超過焊接結構的臨界失穩阻抗(Critical Buckling Resistance， CBR)時，焊接結構將失去穩定性，產生失穩變形。

3 大變形理論

焊接失穩變形屬于彈性穩定性的研究范疇，是一種力學的非線性響應。其中，位移與應變之間的關系反映著彈性體變形的幾何特性，也是實現用數值分析方法研究焊接失穩的關鍵。

當一個焊接接頭或者結構的微單元如圖4所示[10]，在焊縫收縮力的作用下，首先會產生一定量的面內收縮，此時在焊縫方向(設為x方向)產生的應變為

(4)

在繼續壓縮的情況下，若焊接接頭或結構失去穩定性，則會在垂直于焊縫方向(y，z方向)產生一定量的位移，其失穩后的長度為

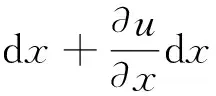
(5)

相對應的應變為

(6)

同理，可分析得出其他各方向受到壓縮失去穩定性時所產生的應變。

失穩發生時對應的角變形可由下式計算求得

(7)

由向量點積運算的定義可知

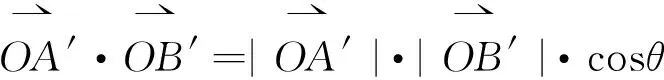
(8)

得到

(9)

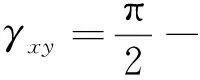
由于考慮的角變形比較小，則有

(10)

大變形理論(有限應變理論)給出的位移與應變的關系也稱為Green-Lagrange應變。在不考慮其中的非線性項時，可簡化為彈性力學中常見的Cauchy應變。

圖4 結構微單元在外力作用下的變形

4 薄板船體結構焊接失穩變形的數值預測

對薄板焊接失穩現象的研究最早起源于日本。1953年，MATSUBUCHI[11]利用試驗的方法，測量薄板結構因焊接產生的失穩變形。同時，通過理論解析，求解出焊接產生的縱向殘余應力，并研究焊后薄板的穩定性。為了保障薄板船體結構的建造精度，WATANABE等[12]經試驗觀察發現：不同厚度鋼板在表面堆焊時，可能產生碗狀(凹-凹型)以及波浪狀(凹-凸型或凸-凹型)等不同類型的焊接變形。同時，WATANABE等[13]還通過測量和計算薄板(板厚1.6mm)堆焊的壓縮熱應力和固有收縮給出了薄板堆焊失穩的最短焊縫長度和最大失穩變形擾度，且與試驗結果相當吻合。

之后的數十年，鮮有焊接失穩變形方面研究的突破性成果發表。隨著船舶輕量化設計和制造理念的提出和推廣以及數值分析技術的廣泛應用，目前對于薄板結構，特別是薄板船體加筋板焊接失穩變形的相關研究，均主要基于數值計算來開展。預測焊接失穩變形的數值分析方法主要有以下幾類。

4.1 瞬態熱彈塑性有限元分析

船體結構的建造中，焊接變形是由傳熱、屈服、熔化、凝固以及相變等物理現象相互耦合產生的。由于傳熱過程對于焊接力學現象有著決定性的作用，而力學現象對于傳熱的影響可忽略不計，因此，采用有限元計算考慮其相互耦合作用會增加計算的復雜度并且降低計算效率，因此毫無必要。常見的熱彈塑性有限元分析都只考慮熱分析對力學過程的強作用，即先計算得出不同時刻的溫度分布，再以此為熱載荷施加到彈塑性力學模型中，從而得到殘余應力和焊接變形。

TSAI等[14]使用ABAQUS軟件進行了三維的熱彈塑性有限元方法研究AH36高強鋼薄板表面堆焊產生的失穩變形。在計算過程中，使用了非耦合的熱傳遞-力學分析過程，并且應用大變形理論來考慮失穩變形的非線性幾何響應。同時，指出了焊接失穩的分歧現象開始于焊后的冷卻階段，并將持續到冷卻結束。MICHALERIS等[15]也在ABAQUS中使用了考慮大變形理論的三維熱彈塑性方法來分析不同尺寸的T型焊接接頭的失穩現象，其預測的焊接變形與測量數據有著很好的一致性，但計算過程需要消耗大量的計算機資源，且耗時太長。針對大型薄板船體結構，YANG等[16]在ABAQUS中利用殼單元建立平板堆焊的有限元網格模型，同時在殼單元的厚度方向上使用5個積分點來分析計算厚度方向上的溫度和應變梯度分布。同樣，以移動熱源計算的熱分析結果作為熱載荷來計算焊接殘余應力，再映射全局殘余應力分布到三維的失穩分析模型上，計算得到焊接失穩變形形狀及數值。

從船體結構的典型焊接接頭著手，WANG等[3]使用內部的非耦合熱彈塑性有限元程序(JWRIAN)研究了2.28mm薄板堆焊產生的焊接失穩變形。計算結果給出了與試驗相同的變形模態，然而由于實體單元網格模型很難反映薄板的初始擾度，計算數值與測量結果稍有差別。同時，WANG等[4]運用相同方法分析了板厚為6mm的船體加筋板結構發生扭轉失穩變形的現象。雖然沒有考慮薄板的初始擾度，然而預測結果顯示，無論是變形模態，還是變形量都與實際測量相當一致。可知，當焊接失穩產生足夠大的變形量時，初始擾度的影響則可忽略不計。

綜上所述，瞬態熱彈塑性有限元方法比較適合分析預測焊接接頭或者簡單的船體焊接結構的失穩變形。

4.2 復合的彈性有限元分析

鑒于船體結構的大型化和復雜性，熱彈塑性有限元方法在實際應用中受到限制，許多學者使用了復合的有限元方法來分析船體焊接結構的失穩現象。

焊接固有應變/變形是產生焊接變形的根源，且可通過理論推導、試驗測量以及瞬態熱彈塑性有限元計算來獲得。因此，以固有應變/變形作為焊接等效載荷的彈性有限元方法是分析解決復雜結構焊接失穩變形的有效且理想的數值方法。ZHONG等[17]使用固有應變作為焊接等效載荷，在考慮板結構彈性大變形理論的情況下，再現了焊接失穩變形。DENG等[18]提出使用熱彈塑性有限元計算與基于大變形理論的彈性計算相結合來預測分析焊接失穩變形。其中，非耦合的熱彈塑性有限元方法用來詳細研究各種典型焊接接頭，并獲得固有變形。施加該固有變形并使用界面要素來預測實際船體結構焊接產生的面外變形。WANG等[19]完善了上述復合有限元方法，將與試驗測量對比的熱彈塑性有限元分析得到的固有應變(塑性應變)進行積分求和，得到更加精確的固有變形。并且，應用該方法分析了薄板堆焊接頭、加強筋焊接結構以及真實船體結構的焊接失穩現象。

同時，其他一些學者也采用了相似的方法來分析焊接失穩變形。TSAI等[20]研究了厚度為1.6mm的船用鋁合金板架結構的焊接失穩現象，使用固有收縮應變獲得接頭的焊接殘余應力分布。對于研究的焊接結構而言，如果其變形抵抗能力(橫截面剛度或者慣性矩)過低，則會產生失穩變形。對于薄板船體結構，DEO等[21]稱其為施加塑性應變法，使用二維的非線性瞬態熱力學分析(其力學理象，可作為一個平面應變問題分析)來研究垂直于焊縫橫截面上的焊接熱過程，計算得到熱載荷以及塑性應變，然后再使用小變形理論的彈塑性力學模型，利用不同的熱膨脹系數得到焊接殘余應力，從而獲得施加的焊接載荷。再使用考慮了大變形理論的靜態結構分析，逐步施加載荷并考慮初始擾度，預測焊接失穩變形量，同時計算失穩臨界載荷。對于加載等效焊接載荷的彈性有限元方法，則在預測焊接失穩變形時，需要考慮幾何結構或者施加載荷的不完善性(非理想性)，以此觸發失穩響應[15]。還針對實際中的非理想性情況，進行焊接失穩及變形量的敏感性分析研究。基于美國海軍的實際需求，HUANG等[9]使用基于收縮力的失穩分析來預測船體面板結構的焊接失穩變形。其中，引起焊接失穩變形的熱力相互作用被分為3個計算過程：典型焊接接頭的熱分析、熱應力的彈塑性分析以及考慮所有焊接接頭的整體結構的失穩分析。

4.3 特征值和特征向量計算

通過加載焊接等效載荷的彈性結構分析來預測焊接失穩變形可以有效地提高計算效率，但其計算過程依然需要消耗相當多的計算資源和計算時間。在薄板船體結構的生產中，通過計算得知焊接失穩的臨界條件往往比獲得焊接失穩變形量更有實際意義。因此，很多學者通過對船體結構的剛度矩陣進行特征值分析計算失穩發生的臨界條件，有效避免大量計算，提高分析效率，更有利于改善焊接過程，保障產品精度。

DEO等[21]利用普遍的二維平面應變模型進行非耦合的熱彈塑性有限元分析，計算焊接產生的熱載荷，然后這些熱載荷被以單位熱載荷的形式逐步加載到實際薄板船體結構的三維有限元模型的橫截面上，再通過特征值分析計算焊接結構可能產生的失穩模態以及失穩臨界載荷(CriticalBucklingLoad,CBL)。這里，計算的特征向量僅僅給出失穩的模態，并非失穩的變形量。同時，通過比較AWL和CBL的數值，判斷焊接失穩是否發生。JUNG等[22]使用等效的熱應變將焊接接頭的塑性應變映射到實際船體結構的殼單元模型中，基于此方法，與愛迪生焊接研究所(EdisonWeldingInstitute,EWI)一起開發了Q-WELD程序。在針對不同形式的薄板船體面板結構的焊接制造過程中應用特征值分析，計算得到可能產生的焊接失穩變形模態。

CAMILLERI等[23]在研究薄板結構焊接失穩時，首先使用小變形理論對一個無重力作用以及初始光滑的平板加載焊接產生的熱載荷，得到其剛度矩陣和應力剛度矩陣；然后，應用這些矩陣到實際的焊接結構中做特征值分析，從而計算出該薄板船體加筋板結構可能產生的失穩模態及對應的臨界失穩載荷。HUANG等[9]使用基于熱塑性的失穩分析研究船體板架結構的焊接失穩現象。其中，殘余應力產生的應力剛度矩陣使得失穩分析轉化為求解結構的特征值問題，計算所得到的位移向量就是對應的可能產生的失穩變形模態。

文獻[5-7]使用固有變形作為焊接載荷，對典型的焊接接頭以及實際的船體焊接結構進行了特征值分析。其中：在焊縫方向，由于周圍母材的強拘束作用，縱向固有變形被轉化為縱向收縮力，而在垂直于焊縫的方向上，橫向固有變形被轉化為橫向收縮。基于殼單元模型的特征值分析給出了所有可能產生的失穩模態以及對應的臨界固有變形(縱向收縮力和橫向收縮力)。同時，WANG等[19]針對大型船體加筋板結構中的典型單元結構，使用特征值分析得到產生失穩的臨界壓縮應力。其與彈性穩定性中四邊簡支約束的薄板雙向壓縮失穩的理論分析結果做對比，有著較好的一致性。TAJIMA等[24]也通過分析船體板架結構中底板上由不同焊接過程所引起的壓縮應力，并與理論計算相比較來判斷是否發生焊接失穩。

5 結論

綜上所述，薄板焊接失穩變形因其非線性及不穩定的特性，相關研究至今仍不完善，特別是在輕量化船體結構的建造中依然沒有實用且有效的措施加以預防控制。

本文系統地回顧了數值分析技術在研究薄板焊接接頭，尤其是薄板船體結構焊接失穩變形中的應用現狀。在討論焊接失穩變形的特征和產生機理后，詳細地闡述了作為數值計算基礎的大變形理論，并且分類介紹了不同數值分析方法在預測薄板船體結構焊接失穩變形模態及數值中的研究進展。

[ 1 ] MASUBUCHI K. Analysis of welded structures: residual stresses, distortion and their consequences [M]. Oxford: Pergamon Press, 1980.

[ 2 ] WANG J, RASHED S, MURAKAWA H, et al. Numerical prediction and mitigation of out-of-plane welding distortion in ship panel structure by elastic FE analysis [J]. Marine Structures, 2013, 34(4): 135-155.

[ 3 ] WANG J, YIN X，MURAKAWA H. Experimental and computational analysis of residual buckling distortion of bead-on-plate welded joint[J]. Journal of Materials Processing Technology, 2013, 213(8): 1447-1458.

[ 4 ] WANG J, SHIBAHARA M, ZHANG X, et al. Investigation on twisting distortion of thin plate stiffened structure under welding[J]. Journal of Materials Processing Technology, 2012, 212(8): 1705-1715.

[ 5 ] MA N, WANG J，OKUMOTO Y. Out-of-plane welding distortion prediction and mitigation in stiffened welded structures[J]. International Journal of Advanced Manufacturing and Engineering, 2016, 84(5): 1371-1389.

[][]

[ 6 ] WANG J, RASHED S， MURAKAWA H. FE analysis of buckling behavior caused by welding in thin plates of high tensile strength steel[J]. Journal of Materials Engineering and Performance, 2014, 23(12): 4358-4365.

[ 7 ] WANG J, RASHED S, MURAKAWA H. Mechanism investigation of welding induced buckling using inherent deformation method[J]. Thin-Walled Structures, 2014, 80(1): 103-119.

[ 8 ] MICHALERIS P, DEBICCARI A. A predictive technique for buckling analysis of thin section panels due to welding[J]. Journal of Ship Production, 1996, 12: 269-275.

[ 9 ] HUANG T D,DONG P, DECAN L, et al. Fabrication and engineering technology for lightweight ship structures, part 1: distortions and residual stresses in panel fabrication [J]. Journal of Ship Production, 2004, 20(1): 43-59.

[10] TIMOSHENKO S P. Theory of elastic stability[M]. 2nd Ed. Mc Graw-Hill Book Co,1936,29(1):220.

[11] MASUBUCHI K. Buckling type deformation of thin plate due to welding [C]//Proceedings of the 3rd Japan National Congress for Applied Mechanics, 1953.

[12] WATANABE M, SATOH K. On the type of distortion in various welded joints: shrinkage distortion in welded joint (Report 5)[J]. Quarterly Journal of the Japan Welding Society, 1957, 26: 399-405.

[13] WATANABE M, SATOH K. Fundamental study on buckling of thin steel plate due to bead-welding[J]. Yosetsu Gakkai Shi/Journal of the Japan Welding Society, 1958, 27(6): 313-320.

[14] TSAI C, HAN M S, JUNG G H. Investigating the bifurcation phenomenon in plate welding[J]. Welding Journal, 2006, 85(7): 151-162.

[15] MICHALERIS P, ZHANG L, BHIDE S R, et al. Evaluation of 2D, 3D and applied plastic strain methods for predicting buckling welding distortion and residual stress [J]. Science and Technology of Welding and Joining, 2013, 11(6): 707-716.

[16] YANG Y P, DONG P. Buckling distortions and mitigation techniques for thin-section structures[J]. Journal of Materials Engineering and Performance, 2012,21(2):153-160.

[17] ZHONG X M, MURAKAWA H, UEDA Y. Buckling behavior of plates under idealized inherent strain[J]. Transactions of JWRI, 1995, 24(2): 87-91.

[18] DENG D, MURAKAWA H. FEM prediction of buckling distortion induced by welding in thin plate panel structures[J]. Computational Materials Science, 2008, 43(4): 591-607.

[19] WANG J, MA N, MURAKAWA H. An efficient FE computation for predicting welding induced buckling in production of ship panel structure [J]. Marine Structures, 2015, 41: 20-52.

[20] TSAI C L, PARK S C, CHENG W T. Welding distortion of a thin-plate panel structure[J]. Welding Journal, 1999, 78(5): 156-165.

[21] DEO M V, MICHALERIS P, SUN J. Prediction of buckling distortion of welded structures[J]. Science and Technology of Welding and Joining, 2013, 8(1): 55-61.

[22] JUNG G, HUANG T D, DONG P, et al. Numerical prediction of buckling in ship panel structures[J]. Journal of Ship Production, 2007, 23(3): 171-179.

[23] CAMILLERI D, COMLEKCI T， THOMAS G. Thermal distortion of stiffened plate due to fillet welds computational and experimental investigation[J]. Journal of Thermal Stresses, 2006, 29(2): 111-137.

[24] TAJIMA Y, RASHED S, OKUMOTO Y, et al. Prediction of welding distortion and panel buckling of car carrier decks using database generated by FEA [J]. Transactions of JWRI, 2007, 36: 65-71.

Progress of Numerical Analysis on Welding Buckling of Thin Plate Ship Structures

WANG Jiangchao

(School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074， Hubei, China)

The numerical analysis on welding buckling of fillet welded joints, thin plate ship structures wes reviewed. The target is to discuss the variety characteristics of welding buckling, and clarify its generation mechanism. Large deformation theory as mathematical fundament is introduced. The present situation and development of the numerical analysis methods,such as transient thermal-elastic-plastic FE analysis, elastic FE analysis and eigenvalue analysis, to predict welding buckling mode are introduced.

thin plate ship structure; welding buckling; FE analysis; large deformation theory; eigenvalue analysis

王江超(1983-)，男，工學博士，副教授，博士生導師，研究領域為船舶與海洋結構物設計制造

1000-3878(2017)02-0073-06