粒子濾波的噪聲相關下單步延遲無序量測更新算法
趙 凱, 胡建旺, 吉 兵
(軍械工程學院 信息工程系,河北 石家莊 050003)
計算與測試
粒子濾波的噪聲相關下單步延遲無序量測更新算法
趙 凱, 胡建旺, 吉 兵
(軍械工程學院 信息工程系,河北 石家莊 050003)
在目標跟蹤系統中,因通信延遲等原因會出現傳感器量測無序地到達融合中心的現象,將這些量測稱為無序量測(OOSM)。針對過程噪聲、量測噪聲相關的非線性系統中出現的無序量測問題,在現有算法基礎上,提出了一種可處理單步延遲無序量測的新算法。在前向預測濾波框架下,對系統方程去相關化,并利用粒子濾波(PF)進行狀態估計。仿真結果驗證了算法的有效性。
無序量測; 非線性; 噪聲相關; 粒子濾波
0 引 言
在集中式目標跟蹤系統中,各傳感器的通信延遲、預處理時間與采樣速率等存在差別,會有傳感器信息不能同步到達融合中心的現象出現,這種現象稱為異步現象[1,2]。在此情形下,對于同一個目標,若有較早時刻產生的量測在較晚時刻產生的量測之后到達融合中心,則稱這些量測為無序量測(out-of-sequence measurement,OOSM)。
目前,直接更新法是實時處理OOSM問題的主流濾波方法,即融合中心存儲目標的狀態估計與估計誤差協方差矩陣,直接利用收到的OOSM對當前狀態估計進行再更新,得到新的目標狀態充分估計量[3]。直接更新法有存儲量、計算量較小,沒有輸出延遲等優點,因此,學者們在此濾波思想下先后提出了A1,B1,AA1,FPFD[3]等線性系統下的濾波算法。
對于弱非線性高斯系統,文獻[4]提出EKF—A1算法,將非線性系統線性化,再應用已有的A1算法,這種算法較為簡單,但可能存在較大的濾波誤差[4];文獻[4]還提出使用UT變換求解非線性量測方程的雅可比矩陣或海賽因矩陣,但近似誤差較大,且當系統方程為非線性時無法求解。對于強非線性系統,文獻[5,6]推導出包含OOSM的后驗概率密度,提出了基于粒子濾波的OOSM處理算法。當傳感器系統處于共同的噪聲環境中時,常會出現過程噪聲與量測噪聲相關的情形。文獻[7,8]分別給出了解決噪聲相關的OOSM問題的濾波算法,但對非線性系統中OOSM問題無法處理。
本文提出在前向預測濾波框架下,對非線性系統方程進行恒等變換,從而去相關化,再利用粒子濾波對系統狀態進行更新。算法可有效處理單步延遲OOSM問題。
1 問題描述
假定非線性離散時間系統如下
xk=fk,k-1(xk-1)+Γk,k-1wk,k-1
(1)
zk=hk(xk)+vk
(2)
式中xk與zk分別為n維狀態向量和m維量測向量;fk,k-1(·)為n維非線性狀態轉移矩陣,hk(·)為非線性量測函數;wk,k-1,vk分別為p維系統噪聲和m維量測噪聲,均為高斯白噪聲;Γk-1為n×p維噪聲輸入矩陣。
假設1wk,k-1和vk為相關的高斯白噪聲,其統計特性如下
式中Qk為非負定對稱陣,Rk為正定對稱陣,δkj為krone-cker-δ函數。
假設2 初始狀態x(0)與wk,k-1、vk互不相關,且服從高斯正態分布,其均值、協方差矩陣為
由式(1)可得
xk=fk,d(xd)+Γk,dwk,d
(3)
假定在t=tk時刻,融合中心已獲得后驗分布p(xk|z1∶k),進而得到狀態向量的充分統計量
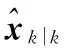
(4)
式中Zk為t=tk時刻累積量測值。
隨后,來自t=td時刻的量測
zd=hd(xd)+vd
(5)
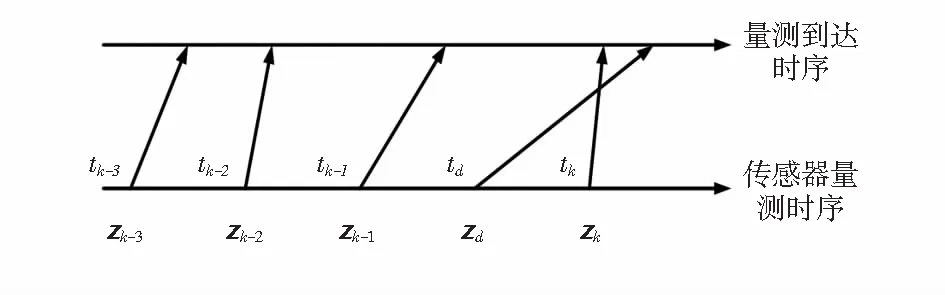
圖1 單步延遲無序量測
2 算法設計
針對上節給定的非線性離散系統,考慮同一時刻過程噪聲與量測噪聲相關的情形,提出解決單步延遲OOSM問題的濾波算法。算法首先根據最小均方誤差準則,將系統方程作恒等變形,實現噪聲去相關化[9]。其次,基于前向預測方法,在有序狀態轉移方式下[10],用粒子濾波算法[11,12]處理延遲到達的量測。
2.1 噪聲去相關化
貝葉斯估計要求系統中各種噪聲互不相關,故式(1),式(2)表示的非線性離散時間系統不能直接進行貝葉斯估計。因此,先將系統方程作恒等變換,去除兩種噪聲的相關性,隨后進行濾波估計。去相關化過程如下所述。
將式(2)變形為
zk-hk(xk)-vk=0
(6)
將上式代入系統方程(1)
xk=fk,k-1(xk-1)+Γk-1wk,k-1+Jk-1[zk-1-
hk-1(xk-1)-vk-1]
=fk,k-1(xk-1)+Jk-1[zk-1-hk-1(xk-1)]+
Γk-1wk,k-1-Jk-1vk-1
(7)
易知式(7)與式(1)等價,其中
Ψk,k-1(xk-1)=fk,k-1(xk-1)+Jk-1[zk-1-hk-1(xk-1)]
(8)
(9)
式中Jk-1為待定系數。
(10)
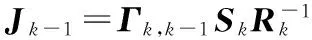
(11)
zk=hk(xk)+vk
(12)
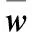
(13)
(14)
(15)
2.2 噪聲相關下單步延遲無序量測更新算法
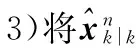

1)將式(1),式(2)所表示的原始運動方程轉換為去除相關性的運動方程(11),式(12)。
2)用PF計算重構航跡:
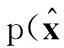
b.各粒子一步預測為
(16)
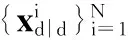
(17)
歸一化得到
(18)
可計算出狀態估計及其估計誤差協方差矩陣為
(19)
(20)
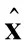
由此,得到了基于粒子濾波的噪聲相關下單步延遲OOSM更新算法。算法在前向預測框架下,對系統方程去相關化,并利用粒子濾波進行狀態估計。算法將已有估計近似為量測值進行再次濾波。相比于現有算法,新算法有更好的濾波效果,這主要因為:去除了系統的噪聲相關性,減小了處理實際系統OOSM問題的濾波誤差;新算法采用前向濾波,不需要儲存大量粒子及權重,減小了算法存儲量。
此外,算法中可以采用優選分布采樣濾波,如不敏卡爾曼粒子濾波、擴展卡爾曼粒子濾波等作為基礎濾波算法,在粒子產生時融入觀測信息,進一步提高了粒子的質量和效能。
3 仿真實驗
采用二維空間中運動模型
xk=Fk,k-1xk-1+Γk,k-1wk,k-1
(21)
zk=h(xk)+vk
(22)
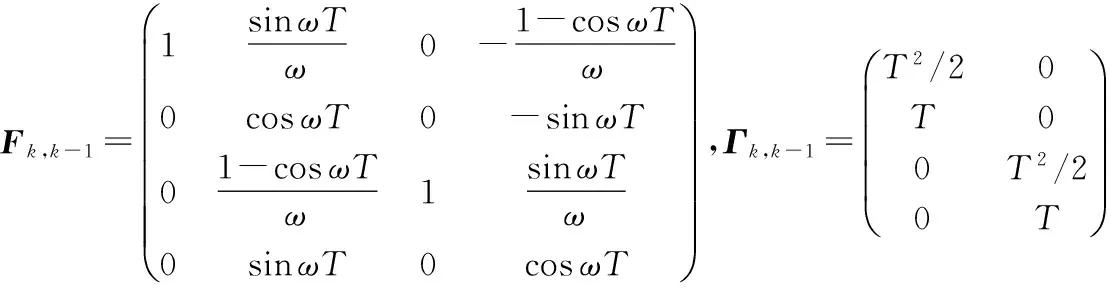
γ,θ分別為目標的距離和偏轉角,量測方程可表示為
(23)
采樣周期T=1,初始值為x0=[20 -2 10 -1]T,P0=I,ω=π/9,采樣粒子數為N=500。
假設傳感器獲得5個量測,由于有OOSM,最后收到的量測排列順序為:z1,z2,z4,z3,z5。在此,分別采用不同算法處理這組量測,以驗證算法性能。
1)實驗1,采用文獻[6]算法處理含OOSM的量測序列z1,z2,z4,z3,z5。
2)實驗2,采用新算法處理含OOSM的量測序列z1,z2,z4,z3,z5。
3)實驗3,采用丟棄量測法處理量測序列,即只處理z1,z2,z4,z5。
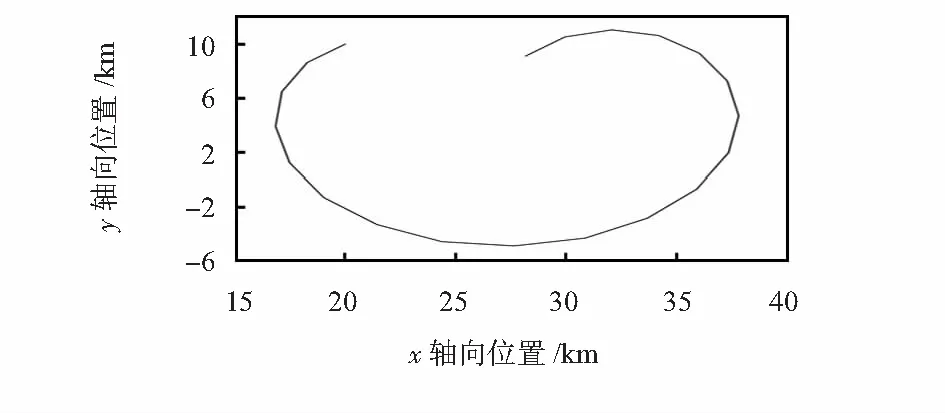
圖2 目標運動軌跡
在此,分別采用不同算法處理這組量測,以驗證算法性能。表1給出了最后時刻濾波器輸出的位置均方根誤差(RMSE)與協方差矩陣的跡(trace)。圖3給出3種實驗所得x軸向、y軸向的估計與真實值的比較。進行500次MonteCarlo仿真。
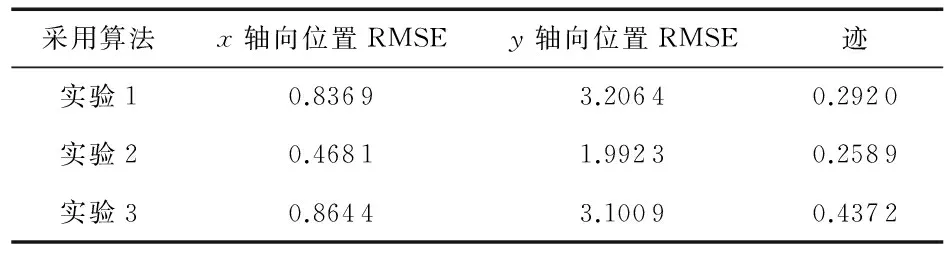
表1 不同實驗結果對比
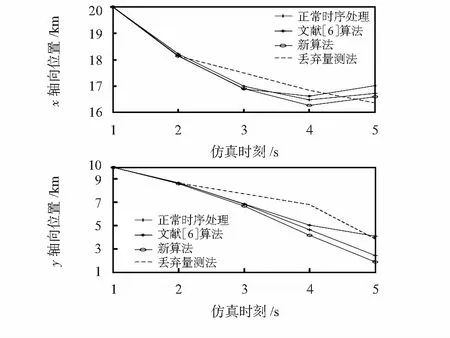
圖3 x軸向與y軸向估計
通過比較表1和圖3中的數據與結果,可以得到以下結論:
1)將實驗2結果與實驗3比較,可以看出,本文算法估計精度要優于丟棄量測法,且接近于真實值,說明本文算法可有效處理OOSM。
2)對比實驗2與實驗1結果,可以看出在處理延遲到達的量測z3時,兩種算法估計精度基本相當,且在最新時刻實驗2結果優于實驗1。說明噪聲去相關化處理的有效性。
3)對比圖3中時刻 位置估計,可以看出實驗1結果有發散趨向,證明了噪聲去相關處理的必要性。
4)實驗2誤差協方差矩陣的跡最小,新算法濾波穩定性優于其它兩種算法。
4 結 論
針對非線性系統同一時刻過程噪聲與量測噪聲相關的情形,給出了基于前向預測的單步延遲OOSM更新算法。1)將系統方程進行恒等變換,去除了噪聲相關性;2)在前向預測框架內,借助粒子濾波器處理OOSM,實現狀態的更新。新算法處理的是單步延遲OOSM問題,今后還可以研究針對多步延遲的問題。此外,對于多傳感器目標跟蹤系統,還可能存在不同傳感器的量測噪聲相關的情形,對此還有待于進一步研究。
[1] 韓崇昭.多源信息融合[M].北京:清華大學出版社,2006.
[2] 王洪鋒,周 磊,單甘霖.國外軍事信息融合理論與應用的研究進展[J].電光與控制,2007,14(4):13-18.
[3] 吳衛華,江 晶.無序量測問題研究綜述[J].傳感器與微系統,2014,33(12):5-9.
[4] 陳金廣,李 潔,高新波.基于UT變換的單步滯后無序量測算法[J].中國科學:信息科學,2011(5):638-648.
[5] Zhang S,Barshalom Y.Out-of-sequence measurement processing for particle filter:Exact Bayesian solution[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(4):2818-2831.
[6] Berntorp K,Robertsson A,Arzen K E.Rao-blackwellized particle filters with out-of-sequence measurement processing[J].IEEE Transactions on Signal Processing,2014,62(24):6454-6467.
[7] 胡建旺,袁 丁,吉 兵,等.噪聲相關下的一步延遲無序量測濾波算法[J].電光與控制,2013(10):69-72.
[8] 高 蕊,秦超英,張希彬.無序量測的狀態更新估計算法[J].傳感技術學報,2006,19(2):501-503.
[9] 錢華明,葛 磊,黃 蔚,等.基于貝葉斯估計噪聲相關下的CKF設計[J].系統工程與電子技術,2012,34(11):2214-2218.
[10] 黃細鳳,吳欽章.順序更新式無序量測處理算法[J].傳感技術學報,2012,25(2):224-228.
[11] 張 淼.基于粒子濾波的機動目標跟蹤方法研究[D].石家莊:軍械工程學院,2008.
[12] 侯 靜,景占榮,羊 彥.遠距離干擾環境下目標跟蹤的擴展卡爾曼粒子濾波算法[J].電子與信息學報,2013(7):1587-1592.
[13] Kitagawa Genshiro.Monte Carlo filter and smoother for non-Gaussian nonlinear state space models[J].Journal of Computational & Graphical Statistics,2012,5(1):1-25.
Update algorithm on one-step-lag out-of-sequence measurement with correlated noise based on particle filtering
ZHAO Kai, HU Jian-wang, JI Bing
(Department of Information Engineering,Ordnance Engineering College,Shijiazhuang 050003,China)
In target tracking system,sensor measurements may arrive at the fusion center out of sequence because of communication delays,and these measurements are called out-of-sequence measurement(OOSM).On the basis of existing algorithm,a new algorithm is proposed,which can solve one-step-lag OOSM problem occur in process noise and the measurement noise correlated in nonlinear system.By combing the framework of the forward prediction filtering, wipe off the correlation,and use particle filtering to estimate the state.Simulation results verify the effectiveness of the proposed algorithm.
out-of-sequence measurement(OOSM); nonlinear; correlated noise; particle filtering(PF)
10.13873/J.1000—9787(2017)05—0141—04
2016—06—13
TP 391
A
1000—9787(2017)05—0141—04
趙 凱(1991-),男,碩士研究生,主要研究方向為多源信息融合,目標跟蹤,E-mail:609587194@qq.com。

