節點類型擴展潮流計算的靈敏度分析

王宗杰， 郭志忠

(哈爾濱工業大學 電氣工程及自動化學院， 哈爾濱 150001)

節點類型擴展潮流計算的靈敏度分析

王宗杰， 郭志忠

(哈爾濱工業大學 電氣工程及自動化學院， 哈爾濱 150001)

為改善傳統靈敏度對潮流的計算分析，在PQ, PV, Vθ三類節點類型基礎上，提出了基于節點類型擴展潮流計算的靈敏度計算方法. 采用PQV，Qθ，QV，PQVθ等擴展節點類型推導了在節點類型擴展潮流計算的修正方程基礎上的相關常用的靈敏度計算公式. 算例分析結果表明:在潮流計算中含有新的擴展節點類型時，常規靈敏度分析方法的準確性明顯下降，而使用基于節點類型擴展潮流計算的靈敏度分析方法仍能獲得很好的精度. 算例驗證了所推導的計算公式的合理性. 提出的基于節點類型擴展潮流的靈敏度計算方法可以提高在大規模系統中的準確性，能夠更好地模擬潮流變化的規律.

電力系統；靈敏度；潮流計算；節點類型；潮流調整

電力系統潮流計算是電網穩態分析的基礎和重要工具. 經過多年的研究，電力系統潮流計算技術已經相當成熟[1-5]. 靈敏度用于分析給定邊界條件的小變化對潮流結果的影響，是潮流分析的重要手段[6-10]. 常規的潮流計算技術僅考慮PQ、PV、Vθ三類節點，傳統的電力設備均可以建模為其中的某一類節點. 然而隨著電網的迅速發展，一些新型的電力設備，尤其是電力電子設備，需要使用新的節點類型刻畫. 另一方面，電網分析計算水平的提高也需要潮流計算具有更好的兼容性. 在這一背景下，考慮其他節點類型的潮流計算技術就成為研究的熱點. 文獻[11]提出了早期的節點類型擴展潮流計算研究，能夠考慮7種節點類型. 文獻[12]引入PQV節點來對統一潮流控制器進行建模并進行潮流計算. 文獻[13]在進行潮流模型匹配計算時使用了含Qq節點的潮流計算. 文獻[14]在節點擴展連續潮流中引入了PQV和P節點來計算電壓穩定臨界點. 文獻[15-16]對節點類型擴展潮流計算進行了系統的研究，并提出了可解性判據，為節點類型擴展潮流計算的進一步發展打下了堅實的基礎. 在此基礎上，文獻[17]提出了基于支路功率選取的擴展潮流計算.

文獻[18]根據光儲置特點實現對含擴展QV節點潮流的求解了堅實的基礎. 靈敏度分析是潮流計算的重要擴展應用，然而當潮流計算的節點類型需要擴展時，尚缺乏有效的方法對新環境下的靈敏度系數進行分析.

本文對節點類型擴展潮流計算的靈敏度分析方法進行了研究. 對常見的靈敏度因子[19]，推導出了其在節點類型擴展潮流計算條件下的計算公式. 基于14節點和118節點系統，比較了常規靈敏度和擴展潮流靈敏度在模擬電網潮流變化時的精度.

1 常規靈敏度計算方法

電力系統潮流分析的靈敏度和分布因子種類很多. 本文選取一些常用的種類，對其常規計算方法進行簡要回顧[19].

1) 發電機機端電壓和負荷節點電壓之間的靈敏度.設全節點的PQ分解法潮流計算無功修正方程為

其中下標G，D分別表示發電機節點和負荷節點，矩陣L為PQ分解法潮流計算中考慮全節點的無功迭代系數矩陣.

建模為PV節點發電機的機端電壓UG對建模為PQ節點的負荷電壓UD靈敏度的計算公式為

2) 發電機無功和負荷節點電壓之間的靈敏度.設式(1)中系數矩陣的逆矩陣為

則發電機的無功QG對負荷電壓UD靈敏度的計算公式為

ΔUD=RDGΔQG.

(4)

3)發電機無功和機端電壓之間的靈敏度.發電機的無功QG對機端電壓UG靈敏度的計算公式為

ΔUG=RGGΔQG.

(5)

4)負荷電壓和變壓器變比之間的靈敏度.負荷節點電壓UD與變壓器變比t之間的靈敏度計算公式為

2 節點類型擴展潮流的靈敏度分析

在節點擴展潮流計算的無功迭代中，將所有節點分為以下4類：1)Q已知，U未知；2)Q、U均未知； 3)Q、U均已知；4)Q未知，U已知. 全節點的無功修正方程為

其中下標數字表示節點所屬的類別. 考慮到已知量和未知量，節點類型擴展潮流計算實際求解的無功修正方程為[15]

以式(7)、(8)為基礎，可推導出節點類型擴展潮流計算的靈敏度計算公式.

1) 發電機機端電壓和負荷節點電壓之間的靈敏度. 在分析發電機機端電壓和負荷節點之間的靈敏度時，發電機節點的機端電壓應為給定量；發電機的機端電壓給定時，其注入無功應為未知量，因此發電機節點應建模為第4類節點. 而負荷節點電壓應為未知量，根據無功注入是否給定，其可能是第1類節點或第2類節點. 此時，式(7)中ΔQ1、ΔQ3、ΔU3均為0. 展開式(7)的第1行和第3行，可以得到

將式(9)整理為矩陣形式，則有

設式(10)中系數矩陣的逆矩陣為

則由式(10)、(11)可以得到發電機電壓與負荷電壓之間的靈敏度關系為

如負荷的Q已知，則靈敏度用式(12)計算，如負荷節點的Q未知，則靈敏度用式(13)計算.

2)發電機無功和負荷節點電壓之間的靈敏度. 當分析發電機無功的靈敏度時，發電機無功作為已知量，而機端電壓作為未知量，因此發電機此時屬于第1類節點. 而負荷節點仍然可能是第1類或第2類節點. 將第1類節點劃分為發電機節點和負荷節點，則式(8)變為

設式(14)的系數矩陣的逆矩陣為

若負荷節點的無功功率已知，其屬于第1類節點，則負荷節點電壓和發電機無功之間的靈敏度關系為

(16)

若負荷節點的無功功率未知，其屬于第2類節點，則負荷節點電壓和發電機無功之間的靈敏度關系為

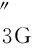
(17)

3)發電機無功和機端電壓之間的靈敏度.由式(14)和式(15)可知，發電機無功和機端電壓之間的靈敏度為

(18)

4)負荷電壓和變壓器變比之間的靈敏度.此時發電機節點仍作為PV節點處理，式(14)簡化為

設式(19)中系數矩陣的逆矩陣為

由于第3類節點的無功注入不變，即ΔQ3=0；若負荷節點的Q已知，則根據式(19)和式(20)可得

(21)

則負荷節點電壓對變壓器變比之間的靈敏度為

若負荷的Q未知，則

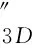
(23)

負荷節點電壓對變壓器變比之間的靈敏度為

3 算 例

3.1 IEEE 14節點系統算例

為了驗證節點類型擴展潮流計算的正確性，本文首先基于IEEE 14節點系統進行算例分析, 14節點系統的結構圖如圖1所示，該系統的詳細數據參見文獻[20].

在圖1的IEEE 14節點的原始數據中，1號節點設為Vθ節點，用紅色標示并連接發電機符號的節點為PV節點，其余節點為PQ節點. 在此基礎上，將7號節點設置為PQV節點，8號節點設置為P型節點. 在本算例中，用以下3類靈敏度分析方法：1) 常規靈敏度分析法：仍保持原節點類型，用第1節所述的常規靈敏度計算公式計算靈敏度；2) 擴展潮流靈敏度分析法：用第2節所述的擴展潮流靈敏度分析方法計算靈敏度；3) 擾動法：在基態潮流解基礎上附加微小擾動并分析靈敏度. 為了保證擾動法的計算結果不受潮流計算收斂誤差的影響，在進行擾動法計算時潮流計算的收斂門檻設置為10-10.

基于IEEE14節點系統，分別使用傳統方法和本文的節點類型擴展的靈敏度分析方法計算靈敏度因子. 部分計算結果見表1. 其中，第1類靈敏度指發電機機端電壓和負荷節點電壓之間的靈敏度；第2類靈敏度指發電機無功功率和負荷節點電壓之間的靈敏度；第3類靈敏度指發電機無功功率和機端電壓之間的靈敏度；第4類靈敏度指負荷電壓和變壓器變比之間的靈敏度.

圖1 IEEE 14節點系統

類型靈敏度分析對象靈敏度擾動法常規靈敏度分析法節點類型擴展潮流靈敏度分析法U2-U140.03100.10270.02831U6-U90.25460.38350.2280U6-U40.11830.17150.1179U3-U140.01840.06290.0173Q2-U140.00100.00390.00102Q6-U90.04280.02180.1277Q6-U40.08010.03580.1534Q6-U110.04240.02190.1243Q2-U20.03270.03780.03733Q6-U60.16800.20880.1861Q3-U30.10410.11540.1137U4-T4-70.18800.12200.20594U9-T4-9-0.1349-0.1980-0.1422U5-T5-60.20630.23270.2233

在表1中，由擾動法確定的靈敏度是經過完整潮流計算得到的，最準確地體現了實際的潮流靈敏度關系. 而其他兩種靈敏度方法均含有線性化的近似，因此，若其結果與擾動法結果相近，則說明其精度較好.

由表1的第4列可以看出，當潮流計算中含有新的節點類型時，仍使用傳統靈敏度分析方法可能會有較大的誤差，當分析對象與具有新類型的節點相關性較強時，相對誤差可能超過200%. 而在表1的第5列中，本文提出的擴展潮流靈敏度分析方法的結果和擾動法接近，相對誤差均在15%以下，具有較好的精度.

3.2 IEEE 118節點系統算例

本文基于118節點系統同樣進行了類似的算例分析，該系統的詳細數據參見文獻[21]. 在原始節點類型的基礎上作如下改動：8號節點由PV節點改為P型節點，19號節點由PV節點改為0型節點，23號節點由PQ節點改為PQVθ節點，39號節點由PQ節點改為PQV節點，53號節點由PQ節點改為Pθ節點，58號節點由PV節點改為QV節點. 靈敏度計算的結果如表2所示.

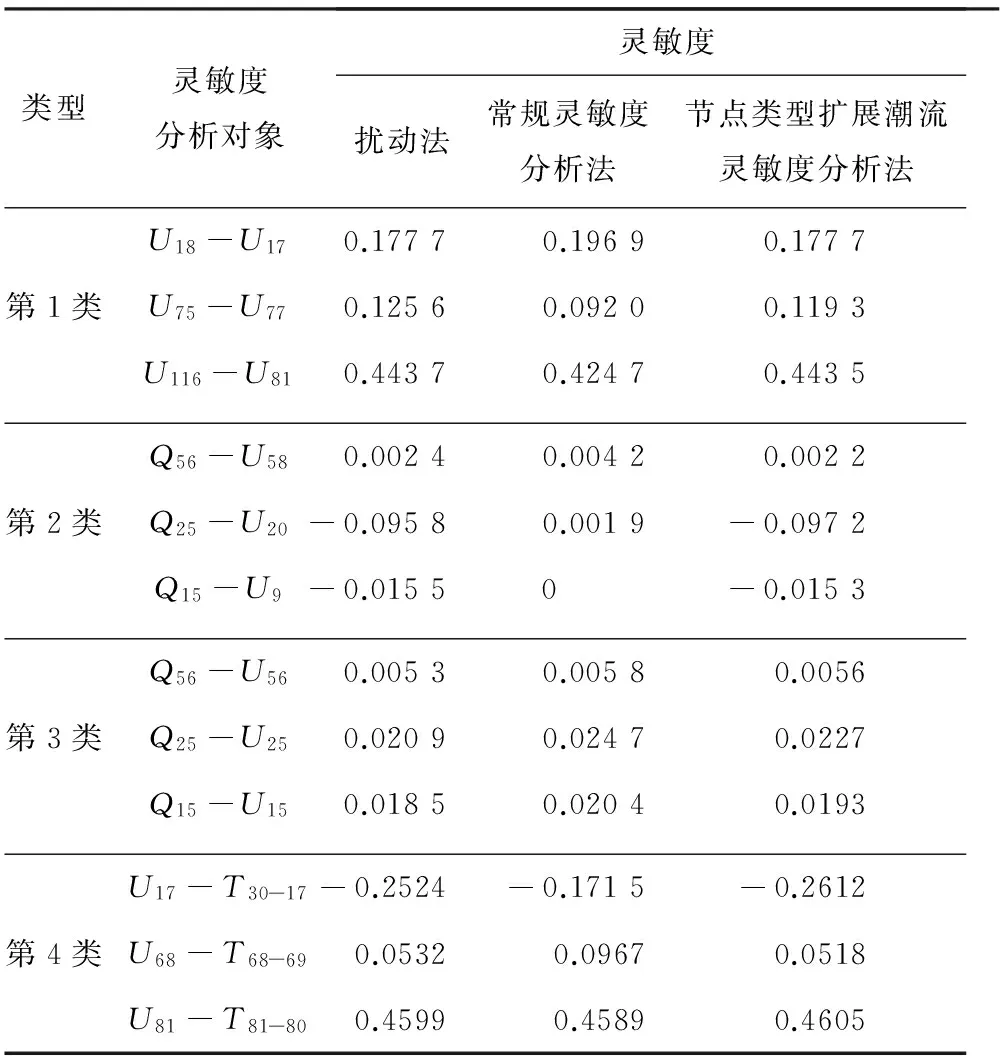
表2 IEEE 118節點系統靈敏度分析結果

通過表2可以看出，與表1相似，當系統中存在新的節點類型時，節點類型擴展潮流靈敏度分析結果的準確程度(表2的第5列)高于傳統靈敏度分析結果(表2的第4列). 例如，對于25號節點無功與20號節點電壓之間靈敏度，傳統方法的計算誤差超過100%，而本文提出的基于節點類型擴展潮流計算的靈敏度分析方法僅有不到1.5%的相對誤差. 表1和表2說明了節點類型擴展潮流靈敏度分析的必要性.

3.3 實際系統算例

為了驗證本文提出的基于節點類型擴展潮流的靈敏度計算方法在更大規模系統的正確性，本文基于我國某省級調度中心的主網架進行算例驗證. 該系統共有262個節點和459條線路. 在原有節點類型的基礎上，設置41號節點為0型節點，189號節點為PQVθ節點，212號節點為P節點，256號節點為PQV節點. 則傳統靈敏度分析方法和本文方法的計算結果對比見表3.

通過表3可以看出，對于規模更大的實際系統，當系統中存在新類型節點時，如果仍然使用傳統方法計算靈敏度，則會產生很大的誤差，如表3的第5列所示；而使用本文提出的節點類型擴展的靈敏度分析方法，誤差會明顯減小，如表3的第7列所示. 算例系統和實際系統的計算結果均表明，本文提出的節點類型擴展靈敏度分析方法是有效的.

表3 某省級實際系統靈敏度分析結果

Tab.3 Sensitivity factor analysis results for provincial practical power system

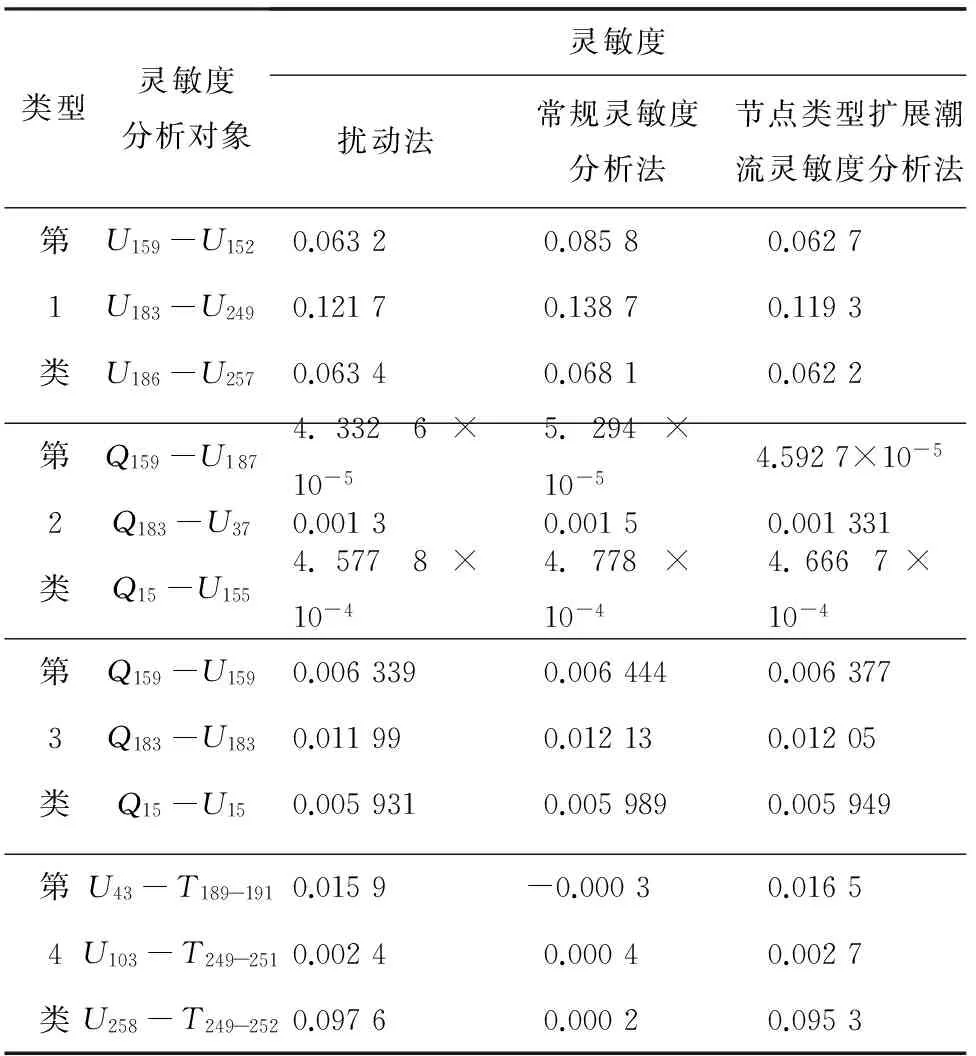
類型靈敏度分析對象靈敏度擾動法常規靈敏度分析法節點類型擴展潮流靈敏度分析法第U159-U1520.06320.08580.06271U183-U2490.12170.13870.1193類U186-U2570.06340.06810.0622第Q159-U1874.3326×10-55.294×10-54.5927×10-52Q183-U370.00130.00150.001331類Q15-U1554.5778×10-44.778×10-44.6667×10-4第Q159-U1590.0063390.0064440.0063773Q183-U1830.011990.012130.01205類Q15-U150.0059310.0059890.005949第U43-T189-1910.0159-0.00030.01654U103-T249-2510.00240.00040.0027類U258-T249-2520.09760.00020.0953

4 結 論

1)推導出了基于節點類型擴展潮流計算的靈敏度計算公式，而常規的靈敏度分析方法僅考慮PQ、PV、Vθ三類節點.

2)算例結果表明，在潮流計算中含有新的節點類型時，常規靈敏度分析方法的準確性明顯下降，而使用基于節點類型擴展潮流計算的靈敏度分析方法仍能保持很好的精度.

3)在實際應用中，可首先分析靈敏度計算中是否涉及新的節點類型. 如不涉及，則可使用傳統靈敏度計算方法；否則應利用本文提出的基于節點類型擴展潮流的靈敏度計算方法.

4)實際上，傳統靈敏度分析方法可以看成是基于節點類型擴展潮流的靈敏度計算方法的一種特殊情形，隨著技術的成熟，基于節點類型擴展潮流的靈敏度計算方法可以取代原有的靈敏度分析方法.

[1] STOTT B, ALSAC O. Fast decoupled load flow[J]. IEEE Transactions on Power Apparatus and Systems, 1974, 93(3): 859-869.

[2] MONTICELLI A, GARCIA A, SAAVEDRA O R. Fast decoupled load flow: hypothesis, derivations, and testing[J]. IEEE Transactions on Power Systems, 1990, 5(4): 1425-1431.

[3] ZHANG X P, PETOUSSIS S G, GODFREY K R. Nonlinear interior-point optimal power flow method based on a current mismatchformulation[J]. IEE Proceedings-Generation, Transmission and Distribution, 2005, 152(6): 795-805.

[4] CHIANG H D, ZHAO T Q, DENG J J, et al. Homotopy-enhanced power flow methods for general distribution networks with distributed generators[J]. IEEE Transactions on Power Systems, 2014, 29(1): 93-100.

[5] SUN H, GUO Q, ZHANG B, et al. Master-slave-splitting based distributed global power flow method for integrated transmission and distribution analysis[J]. IEEE Transactions on Smart Grid, 2015, 6(3): 1484-1492.

[6] PESCHON J, PIERCY D S, TINNEY W F, et al. Sensitivity in power systems[J]. IEEE Transactions on Power Apparatus and Systems, 1968, 87(8): 1687-1696.

[7] CHANG Y C, LIU C C, YANG W T. Real-time line flow calculation using a new sensitivity method[J]. Electric Power System Research, 1992, 62(24): 127-133.

[8] 孫宏斌, 張伯明, 相年德. 準穩態靈敏度的分析方法[J]．中國電機工程學報, 1999, 19(4): 9-13.

SUN Hongbin, ZHANG Boming, XIANG Niande. New sensitivity analysis method under quasi-steady-state for power systems[J]. Proceedings of the CSEE, 1999, 19(4): 9-13.

[9] CHEN Y C, DOMINGUEZ A D, SAUER P W. Measurement-based estimation of linear sensitivity distribution factors andapplications[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1372-1382.

[10]黃根, 羅滇生, 李帥虎,等. 基于綜合靈敏度分析限流的最優斷線措施[J]. 電網技術, 2016, 40(1): 309-315.

HUANG Gen, LUO Diansheng, LI Shuaihu, et al. Optimal line-outage measure based on comprehensive sensitivity analysis to limit short-circuit current[J]. Power System Technology, 2016, 40(1): 309-315.

[11]王魯, 相年德, 王世纓. 廣義潮流計算[J]. 中國電機工程學報, 1990, 10(6): 63-67.

WANG Lu, XIANG Niande, WANG Shiying. Generalized power flow[J]. Proceedings of the CSEE, 2005, 29(23): 19-24.

[12]羅春雷, 孫洪波, 徐國禹. 含PQV節點的潮流計算在UPFC中的應用[J]. 電力系統自動化, 1997, 21(4): 34-36.

LUO Chunlei, SUN Hongbo, XU Guoyu. The application of power flow calculation with PQV node for UPFC[J]. Automation of Electric Power Systems, 1997, 21(4): 34-36.

[13]蔣維勇, 吳文傳, 張伯明，等. 在線安全預警系統中的網絡模型重建[J]. 電力系統自動化, 2007, 31(21): 5-9.

JIANG Weiyong, WU Wenchuan, ZHANG Boming, et al. Network model reconstruction in online security early warning system[J]. Automation of Electric Power Systems, 2007, 31(21): 5-9.

[14]ZHAO J, ZHOU C, CHEN G.A novel bus-type extended continuation power flow considering remote voltage control[C]//IEEE Power & Energy Society General Meeting. Vancouver: IEEE, 2013: 1-5.

[15]郭燁, 吳文傳, 張伯明，等. 節點類型擴展潮流計算的應用研究[J]. 中國電機工程學報, 2011, 31(16): 81-86.

GUO Ye, WU Wenchuan, ZHANG Boming, et al. Application research on bus-type extended load flow[J]. Proceedings of the CSEE, 2011, 31(16): 81-86.

[16]ZHANG Y J, YANG Y Y, LIU Z H. A joint day-ahead scheduling for photovoltaic-storage systems based on extended QV bus-type power flow[C]//International Conference on Smart Grid and Clean Energy Technologies. Offenburg: IEEE, 2015: 18-22.

[17]盧志剛, 程慧琳, 馮磊. 基于支路功率選取的功率擴展潮流計算[J]. 電工技術學報, 2013, 28(6): 208-215.

LU Zhigang, CHENG Huilin, FENG Lei. Extended-power load flow calculation based on selection of branch power[J]. Transactions of China electro-technical society, 2013, 28(6): 208-215.

[18]劉澤槐, 翟世濤, 張勇軍，等. 基于擴展QV節點潮流的光儲聯合日前計劃[J]. 電網技術, 2015, 39(12): 3435-3441.

LIUZekui,ZHAIShitao,ZHANGYongjun,etal.Ajointday-aheadschedulingforphotovoltaic-storagesystemsbasedonextendedQVbus-typepowerflow[J].PowerSystemTechnology, 2015, 39(12): 3435-3441.

[19]張伯明, 陳壽孫, 嚴正．高等電力網絡分析 [M].2版. 北京: 清華大學出版社, 2007: 69-80.

ZHANGBoming,CHENShousun,YANZheng.Advancedelectricpowernetworkanalysis[M]. 2nded.Beijing:TsinghuaUniversityPress, 2007: 69-80.

[20]DABBAGCHII.Powersystemstestcasearchive-14buspowerflowtestcase[EB/OL]. (1993-08-05)[2016-05-14].http://www.ee.washington.edu/research/pstca/pf14/pg_tca14bus.htm.

[21]CHRISTIER.Powersystemstestcasearchive-118buspowerflowtestcase[EB/OL]. (1993-08-23)[2016-05-14].http://www.ee.washington.edu/research/pstca/pf118/pg_tca118bus.htm.

Sensitivity factor analysis for bus type extended load flow

WANG Zongjie, GUO Zhizhong

(School of Electric Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China)

To improve conventional sensitivity factor analysis for load flow calculation that only considers three bus types: PQ, PVandVθ,thispaperproposesasensitivityfactoranalysismethodforbustypeextendedloadflowcalculation.ByconsideringPQV，Qθ，QV，PQVθextendedbustypes,thispaperderivesthesensitivityfactorcalculationformulasbasedonthecorrectequationsofbustypeextendedloadflow.Numericaltestsgiveninthispapershowthat,whennewbustypesareinvolvedinaloadflowcalculation,theprecisionofconventionalsensitivityanalysismethodreducesobviously,whereastheproposedmethodcanstillobtainabetterresult.Italsodemonstratestheeffectivenessofthederivedsensitivityanalysismethod.Byapplyingtheproposedmethod,itcanincreasetheaccuracyinlarge-scalenetworksandbettersimulatethechangeofloadflow.

power systems; sensitivity factor; load flow calculation; bus type; load flow adjustment

(編輯 魏希柱)

10.11918/j.issn.0367-6234.2017.03.005

2016-05-14

國家重點基礎研究發展計劃(2012CB027082)

王宗杰(1990—)，女，博士研究生; 郭志忠(1961—)，男，教授，博士生導師

王宗杰，fylx-001@163.com

TM

A

0367-6234(2017)03-0035-05