基于VMD樣本熵和LS-SVM的滾動軸承故障診斷

趙 磊，夏均忠，李澤華，于明奇，汪治安

(1.軍事交通學院 研究生管理大隊，天津 300161； 2.軍事交通學院 軍用車輛系，天津300161)

?

● 車輛工程 Vehicle Engineering

基于VMD樣本熵和LS-SVM的滾動軸承故障診斷

趙 磊1，夏均忠2，李澤華2，于明奇1，汪治安1

(1.軍事交通學院 研究生管理大隊，天津 300161； 2.軍事交通學院 軍用車輛系，天津300161)

滾動軸承在發生故障時其振動信號會出現調幅、調頻現象，表現出非線性非平穩特征，通過變分模態分解(VMD)可以反映軸承故障特征。首先應用VMD將軸承振動信號分解為一系列模態分量，計算各模態分量的樣本熵并作為特征向量輸入到最小二乘支持向量機(LS-SVM)進行訓練，得到其模型；然后分別應用線性、多項式和高斯徑向基核函數的LS-SVM模型對軸承正常、內圈故障、外圈故障等3種技術狀態的軸承樣本數據進行故障模式識別。結果表明，在較少樣本的情況下，LS-SVM相比于神經網絡，有較高的識別精度，且訓練時間短，能夠有效識別軸承故障類型。

滾動軸承；故障診斷；變分模態分解；樣本熵；最小二乘支持向量機

目前應用于滾動軸承故障診斷的方法有很多，如小波分解、隨機共振[1]、循環平穩[2]、經驗模態分解等。經驗模態分解(empirical decomposition, EMD)是Huang在上個世紀末期提出的一種分析非線性、非平穩信號的遞歸式模態分解方法[3]。EMD存在如模態混疊、端點效應以及過包絡、欠包絡等缺點。鑒于此，Dragomiretskiy K等[4]提出了一種新的非遞歸式自適應模態分解算法——變分模態分解(variational mode decomposition，VMD)。文獻[5]將VMD應用于轉子碰磨故障診斷。文獻[6]將VMD和奇異值分解相結合，提取滾動軸承正常和故障狀況下的特征。

滾動軸承在發生故障時，其振動信號常表現出非線性非平穩特征，而樣本熵作為一種基于非線性動力學方法已應用于軸承故障診斷[7-8]。支持向量機(support vector machine, SVM)在解決小樣本、非線性及高維數等模式識別問題時具有明顯優勢，常應用于軸承故障診斷[9-10]。最小二乘支持向量機(least squares support vector machine, LS-SVM)是支持向量機的一種改進，將傳統支持向量機中解二次規劃問題轉化為求解線性方程組問題，在保證收斂精度的同時也大大降低了求解問題的復雜性，提高了運算效率[11]。

由于單一尺度的樣本熵無法精確地反映軸承的運行狀態，所以首先將滾動軸承振動信號利用VMD分解成多個模態，計算各個模態的樣本熵作為特征向量，然后輸入到最小二乘支持向量機中，自動進行故障模式識別。

1 變分模態分解(VMD)

VMD是一種完全非遞歸的信號分解方法。它可以將任意信號f(t)分解成許多圍繞在中心頻率ωk周圍的模態分量信號。具體步驟為

(1)首先用Hilbert變換計算每個模態uk的相關解析信號以獲得一個單邊頻譜，然后通過加入一個指數項來調整各自估計的中心頻率，把每個模態的頻譜轉移到基帶上，最后通過解調信號的高斯平滑來估計帶寬，即梯度的二范數平方。由此產生了一個由變分問題組成的目標函數：

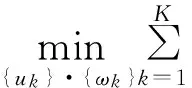
(1)

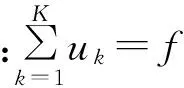
模態的集合為{uk}:={u1，u2，…，uK}，它們的中心頻率為{ωk}:={ω1，ω2，…，ωK}。

(2)通過引入拉格朗日乘子λ和二次懲罰項將上述約束性變分問題轉化為非約束性變分問題。增廣拉格朗日表達式為

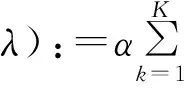
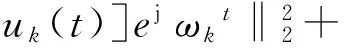
(2)

式中：α為懲罰因子；λ(t)是加強約束。二次懲罰項的作用是提高收斂性。

(3)通過尋找迭代子優化序列中增廣拉格朗日的鞍點，即應用交替方向乘子法(優化算法)求解式(1)的最小化問題。求解式(2)的迭代式為

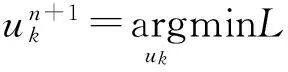
(3)

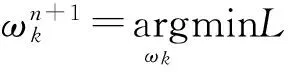
(4)

(5)

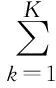
(6)

式中n為迭代次數。式(6)為收斂條件，ε為收斂精度(ε>0)。

利用L2范數下Parseval/Plancherel傅里葉等距在頻域對式(3)～(5)進行求解：

(7)

(8)

(9)

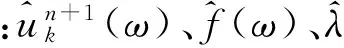
因此，完整的VMD算法實現過程為

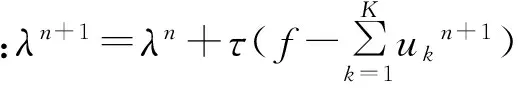
(4)判斷是否滿足式(6)的收斂條件，若滿足則停止迭代，否則返回到步驟(2)。

2 樣本熵

對于一個由N個數據組成的時間序列{x(n)}=x(1)，x(2)，…，x(N)，樣本熵的計算過程為

(1)按序號組成一組維數為m的向量：Xm(1)，Xm(2)，…，Xm(N-m+1)，其中Xm(i)={x(i)，x(i+1)，…，x(i+m-1)}，1≤i≤N-m+1。

(2)定義向量Xm(i)與Xm(j)之間的距離d[Xm(i),Xm(j)]為兩者對應元素中最大差值的絕對值：

d[Xm(i),Xm(j)]=maxk=0，…，m-1(|x(i+k)-x(j+k)|)

(10)

(3)統計Xm(i)與Xm(j)之間的距離小于等于r的j(1≤j≤N-m，j≠i)的數目，記為Bi。在1≤i≤N-m上定義：

(11)

(4)定義B(m)(r)為

(12)

(5)增加維數到m+1，計算Xm+1(i)與Xm+1(j)的距離小于等于r的個數(1≤j≤N-m，j≠i)，記為Ai。并定義：

(13)

(6)定義A(m)(r)為

(14)

Bm(r)是兩個序列在相似容限r下匹配m個點的概率，而Am(r)是兩個序列在相似容限r下匹配m+1個點的概率。樣本熵的定義為

(15)

當N為有限值時，可用下面的公式估計：

(16)

由此可見，樣本熵的值與m，r，N有關。所以如何確定這兩個參數值對于樣本熵的計算十分重要。根據Pincus[12]的研究結果，m=1或2，r=0.1 Std～0.25 Std(Std是原始數據的標準差)時得到的結果具有較為合理的統計特性。基于此，本文研究選用的參數為：m=2，r=0.2 Std。對于數據長度N的選取，長度越大樣本熵越穩定，但過大的數據長度會增加計算時間。所以綜合考慮，選取的數據長度為2 048。

3 最小二乘支持向量機(LS-SVM)

LS-SVM把SVM中二次規劃問題的求解轉化為線性方程組的求解，用等式約束代替不等式約束，用一個分類器解決了多分類器問題，在一定程度上解決了SVM在多分類問題中存在的不足。使得優化問題轉化為

(17)

約束條件為

yi=wTφ(xi)+b+ei，i=1，2，…，l

(18)

式中：φ為非線性變換函數；w∈Rn；ei∈R，b∈R。

為求解該優化問題，引入Lagrange函數：

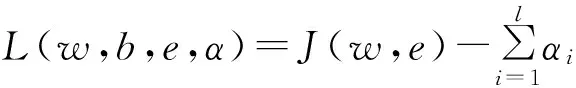
yi+ei}

(19)

式中αi為Lagrange算子。

在極值點處對式(19)中的w,b、e、α分別求偏微分并令其等于零，消掉w和e，得到線性方程：

(20)

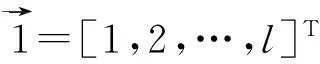
最后用最小二乘法求出a與b。最小二乘支持向量機也由此得名，并且得到分類函數：

(21)

式中K(x,xi)為核函數。

典型核函數有線性核函數、多項式核函數和高斯徑向基核函數，3種核函數的表達形式為

(22)

4 滾動軸承故障診斷

4.1 算法流程

(1)分別采集正常軸承、內圈故障軸承、外圈故障軸承的振動信號；

(2)利用VMD將滾動軸承3種技術狀態的振動信號分別分解成一系列模態分量；

(3)分別計算各技術狀態模態分量的樣本熵，并作為特征向量輸入到LS-SVM；

(4)將上述特征向量組成的數據集分為訓練樣本和測試樣本，并把訓練樣本輸入支持向量機進行訓練建立LS-SVM模型；

(5)利用模型對測試樣本進行分類，確定軸承的工作狀態和故障類型。

4.2 應用實例

試驗裝置由一個1.5 kW的可控電機、一個聯軸器、一個測功器(加載裝置)，及振動加速度傳感器、轉速計等組成[13]。試驗軸承安裝在電機的驅動端，振動加速度傳感器固定在試驗軸承12點鐘方向上方的機架上，通過測功器調整試驗軸承的負載，利用16通道數據采集卡完成試驗軸承振動信號的采集。試驗軸承為SKF 6205-2RS深溝球軸承。使用電火花在軸承內、外圈加工直徑均為0.18 mm(深度均為0.28 mm)的圓坑，模擬內、外圈故障。電機轉速為1 750 r/min。采樣頻率為12 kHz，采樣點數為2 048。

滾動軸承正常、內圈故障、外圈故障振動信號的時域波形及頻譜如圖1所示。從圖中可以發現軸承振動信號時域波形由于噪聲的影響無法識別故障特征，且頻譜圖中出現了一些高頻成分。

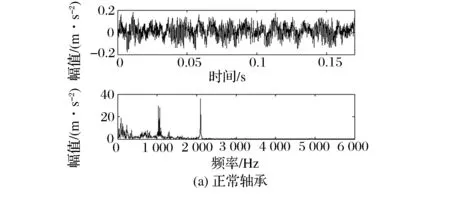
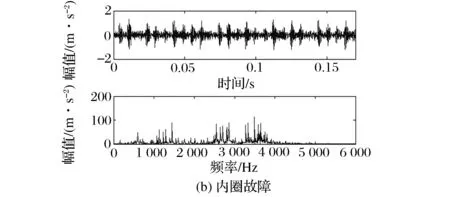
圖1 軸承振動信號的時域波形及頻譜

對軸承振動信號進行VMD分解，其結果如圖2所示。

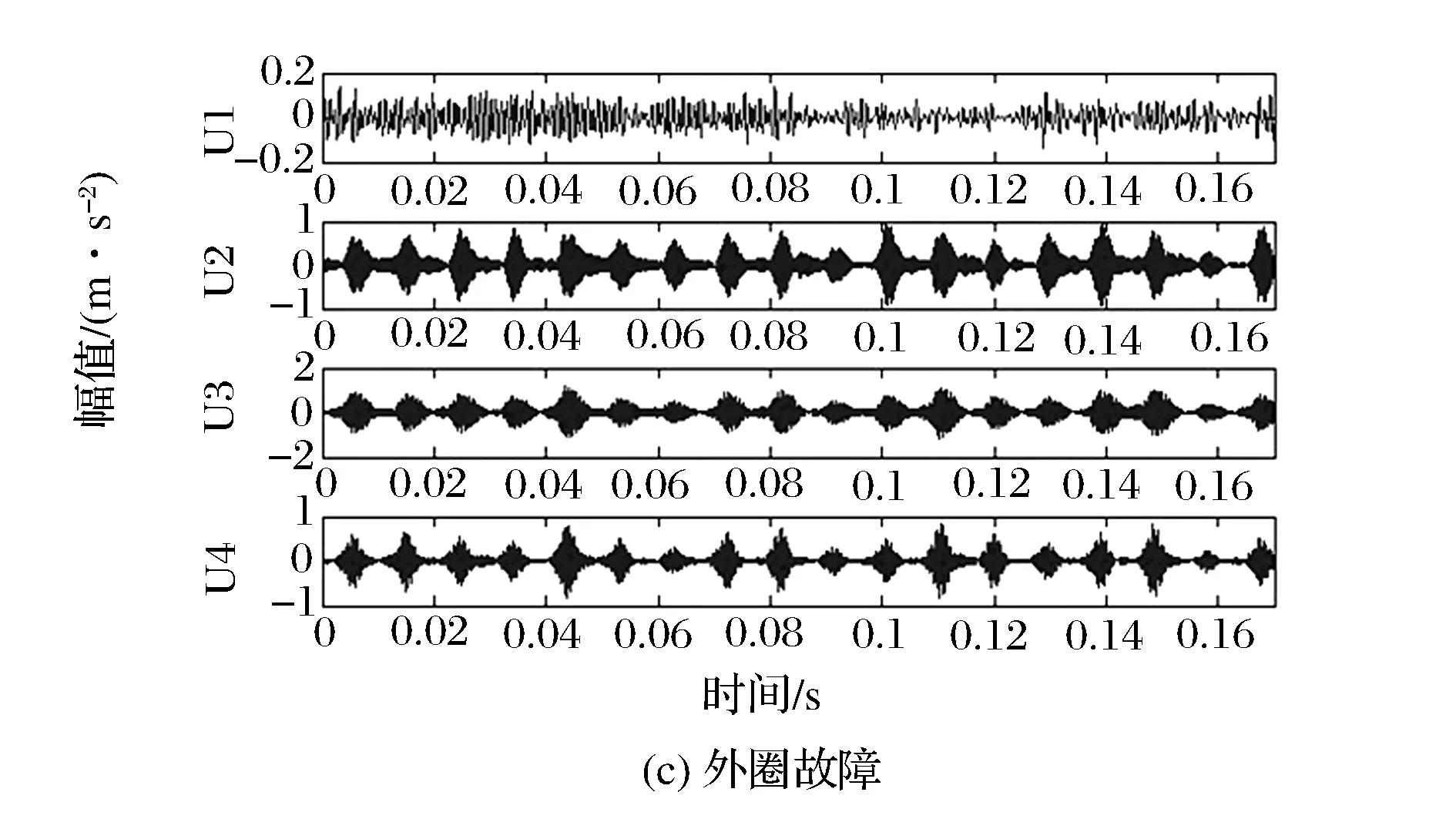
圖2 VMD分解結果

然后計算各模態分量的樣本熵作為特征向量輸入到LS-SVM進行訓練，得到LS-SVM模型。軸承3種技術狀態數據集見表1，其中每種技術狀態共提取50個樣本、訓練集30個、測試集20個，均為隨機抽取分配。

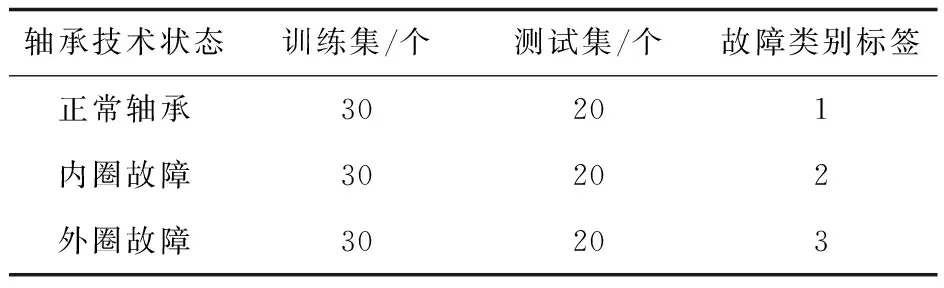
表1 數據集

選用“一對一”多分類模式識別方法，并分別用線性核函數、多項式核函數及高斯徑向基核函數對軸承3種技術狀態樣本進行分類，故障分類結果見表2。其中多項式核函數的參數d=3，高斯徑向基核函數參數γ=1，誤差懲罰因子C=100。從表2可以看出基于3種核函數的LS-SVM分類模型訓練時間相差不大，但在分類準確率方面，基于高斯徑向基核函數要明顯優于其他兩種。較高的分類準確率驗證了本文提出的滾動軸承故障診斷方法的有效性。

表2 LS-SVM故障分類結果

為了進一步說明LS-SVM的優越性，分別利用LS-SVM和神經網絡進行訓練，測試結果見表3。在較少樣本的情況下，LS-SVM和神經網絡對故障類型識別率分別為100%和66.67%，LS-SVM取得較高的識別精度，且LS-SVM的訓練時間較神經網絡大幅度縮短。這表明LS-SVM能有效地解決小樣本軸承故障的分類問題。

表3 LS-SVM和神經網絡識別性能比較

5 結 語

滾動軸承在發生故障時，其振動信號是一種非線性非平穩性信號，利用樣本熵可以提取出其故障特征信息。但由于單一尺度的樣本熵無法精確全面地提取出特征參數，故利用VMD將信號分解成多個模態，并計算各個模態的樣本熵作為特征向量輸入到最小二乘支持向量機中。通過試驗驗證了該方法的有效性，可以精確地識別出軸承不同故障類型。

[1] 夏均忠,劉遠宏,馬宗坡,等.基于調制隨機共振的微弱信號檢測研究[J].振動與沖擊,2012,31(3):132-135．

[2] ZHOU Y, CHEN J, DONG G M, et al. Application of the horizontal slice of cyclic bispectrum in rolling element bearings diagnosis[J]. Mechanical Systems and Signal Processing, 2012, 26(1):229-243.

[3] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A, 1998, 454(1971):903-995.

[4] DRAGOMIRETSKIY K，ZOSSO D. Variational mode decomposition[J]. IEEE Transaction on Signal Processing, 2014,62(3)：531-544．

[5] WANG Y X, MARKERT R, XIANG J W, et al. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system[J].Mechanical Systems and Signal Processing, 2015,60(29):243-251．

[6] 劉長良,武英杰,甄成剛.基于變分模態分解和模糊C均值聚類的滾動軸承故障診斷[J].中國電機工程學報,2015,35(13)：3358-3365．

[7] 趙志宏,楊紹普.一種基于樣本熵的軸承故障診斷方法[J].振動與沖擊,2012,31(6):136-140．

[8] 蘇文勝,王奉濤,朱泓,等.基于小波包樣本熵的滾動軸承故障特征提取[J].振動、測試與診斷,2011,31(2):162-166．

[9] LIU R N, YANG B Y, ZHANG X L, et al. Time-frequency atoms-driven support vector machine method for bearings incipient fault diagnosis[J]. Mechanical Systems and Signal Processing, 2016,75(30):345-370．

[10] LI Y B, XU M Q, WEI Y, et al. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree[J]. Measurement, 2016,60(7):80-94．

[11] LIU X F, BO L, LUO H L. Bearing faults diagnostics based on hybrid LS-SVM and EMD method[J]. Measurement,2015,59(1):145-166.

[12] PINCUS S M. Assessing serial irregularity and its implications for health[J]. Ann.N.Y.Acad.Sci, 2002,954(29):245-267．

[13] SMITH W A, RANDALL R B. Rolling element bearing diagnostics using the Case Western Reserve University data：a benchmark study[J]. Mechanical Systems and Signal Processing, 2015,64(18):100-131.

(編輯：張峰)

Fault Diagnosis of Rolling Bearing Based on VMD Sample Entropy and LS-SVM

ZHAO Lei1, XIA Junzhong2, LI Zehua2, YU Mingqi1, WANG Zhian1

(1.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China;2.Military Vehicle Department, Military Transportation University, Tianjin 300161, China)

The vibration signal of rolling bearing may show amplitude and frequency modulation while failures happen, and the nonlinear non-stationary characteristics can reflect the fault diagnosis of bearing through variational mode decomposition(VMD). Firstly, the vibration signal of bearing were decomposed into several modal components with VMD and the sample entropy of each modal component was calculated and inputted into least squares support vector machine(LS-SVM)as feature vector, and the model was obtained. Then, the bearing sample data under three technology states (normal, inner race fault and outer race fault) was identified by LS-SVM model with linearity, polynomial and Gaussian radial basis kernel function respectively. The result shows that LS-SVM has better identification accuracy and shorter training time with less samples comparing with neural network, and it can identify the fault type of bearing effectively.

rolling bearing; fault diagnosis; variational mode decomposition (VMD); sample entropy; least squares support vector machine (LS-SVM)

2016-10-12；

2016-11-17．

趙 磊(1991—)，男，碩士研究生； 夏均忠(1967—)，男，博士，教授，碩士研究生導師.

10.16807/j.cnki.12-1372/e.2017.04.011

TH133.33

A

1674-2192(2017)04- 0043- 05