初中生數學學習興趣問卷編制與現狀調查

吳洪艷，劉曉琳

?

初中生數學學習興趣問卷編制與現狀調查

吳洪艷1，劉曉琳2

（1．內江師范學院教育科學學院，四川內江 641100；2．隆昌一中，四川內江 642150）

以國外學習興趣四階段理論為指導，自編初中生數學學習興趣初始問卷．經因素分析確定了激發的情境興趣、維持的情境興趣與個體興趣3因素17題項的正式問卷．運用問卷對588名初中生進行調查，結果發現：（1）中國初中生數學情境興趣尚可，個體興趣亟待提高．（2）情境興趣存在顯著的校際、年級與班際差異，個體興趣只存在班際差異，不存在校際與年級差異．（3）學校教學理念與教學條件，特別是教師，是影響初中生數學學習興趣最為重要的因素．

初中生；數學學習興趣；問卷編制；現狀調查；原因分析；教育建議

1 引 言

學習興趣是影響學習的重要變量．國外學者對學習興趣進行了深入系統的研究，提出了具有很強解釋效應與指導意義的學習興趣產生根源與機制的理論[1~2]，對學習興趣的內部結構[3~7]及其影響與作用[8~10]進行了大量的實證研究．個體興趣與情境興趣的劃分是國外學習興趣結構研究的標志性成果．前者被界定為一種個人長期、深入地與某一主題或領域相聯系而產生的個性傾向；后者被被界定為一種由活動或學習任務的特征對個體產生的吸引力激發的即時的、積極的心理狀態[7，11~12]．Hidi與Renninger[7]在總結前人以及自己對學習興趣長期研究的基礎上，進一步將情境興趣劃分為激發的情境興趣與維持的情境興趣（前者是由短期的情感與認知過程的改變導致的一種興趣的心理狀態，它主要受環境與文本特征的激發；后者是繼前者之后的一種興趣的心理狀態，包括能夠延續一段時間的集中的注意力與堅持力，它主要是由任務的意義性與個人卷入維持的）、將個體興趣劃分為初現的個體興趣與成熟的個體興趣（二者表現為不同程度的肯定的情感、儲存的知識與儲存的價值），從而提出了西方學習興趣結構研究的總結性成果——學習興趣四階段發展理論．學習興趣發展的不同階段具有不同的特點、不同的影響因素與促進措施，因此，了解學生學習興趣所處階段與特點對學生學習興趣的培養具有重要的價值與意義．

數學是學習和研究現代科學技術必不可少的工具，也是中小學最為重要的課程之一．眾多研究發現學習興趣是影響學生數學學習的重要的非智力因素[13~15]，王光明、宋金錦等在編制高中生數學學習非智力特征調查問卷時，將學習興趣作為推動、指引和維持數學學習的認知性動機編入了問卷[16]；焦彩珍發現初中生數學學習興趣、數學學業自我效能和數學學業成績之間存在顯著的正相關[17]．初中階段是學習興趣形成與發展的重要時期，初中數學較大的抽象性與較強的邏輯性使得初中生數學學習容易發生兩極分化現象——如果教師引導得當，學生很容易對數學產生濃厚的學習興趣，反之，則很容易失去對數學的學習興趣甚至放棄數學學習，如戴鳳鳴、姚林調查發現農村數學學困生存在對數學缺乏學習興趣的情意特征[18]．因此，深入分析研究初中生數學學習興趣的特征與影響因素具有特別重要的價值與意義．研究擬以Hidi與Renninger[7]的學習興趣四階段理論的建構為指導編制初中生數學學習興趣問卷，探索中國初中生數學學習興趣的結構，并運用自編問卷進行調查，以了解當前中國初中生數學學習興趣的狀況，并進一步分析原因，繼而提出具有針對性的培養措施．

2 初中生數學學習興趣問卷編制

2.1 項目的搜集與整理

初始問卷以學習興趣四階段理論[7]建構為指導，在廣泛查閱相關文獻與深入訪談基礎上，結合初中生數學學習特點與學習環節編制了69個初始條目．經過反復修訂形成一個56個條目、從非常不符合到非常符合1~5級評分的初中生數學學習興趣預測問卷．56個條目中有13個反向條目，7對對偶檢測．反向條目反向計分，各條目得分越高學習興趣越高．

2.2 項目分析

使用56個條目的預測問卷，對A中學初一到初三每個年級一個好班（學生入學時基礎好，一般教師配備也較好）、一個差班（學生入學時基礎差，一般教師配備也較差），共計358名初中生進行問卷調查，經對偶檢測后保留330名被試，其中初一114人、初二116人、初三100人，女生175人、男生155人．采用SPSS19.0進行項目分析．極端值比較發現高分組（前27%）與低分組（后27%）被試各條目得分差異極其顯著（>0.70，<0.001），表明各條目區分度很好；題總相關發現，所有條目得分與學習興趣總分的相關>0.40，相關非常顯著（<0.01），表明各條目與整體量表同質性高．根據各條目信度分析結果，刪除修正的條目總相關<0.40以及條目刪除后總量表的值大于刪除前總量表值的一個條目；根據共同性與因素負荷分析的結果，刪除共同性<0.20、因素負荷量<0.45的4個條目．項目分析共刪除5個條目，保留51個條目參與探索性因素分析．

2.3 探索性因素分析

采用潛變量建模軟件Mplus4.2對項目分析后的51個條目進行探索性因素分析．首先，對330名預測被試取樣進行適當性檢驗，得到KMO值為0.966，Bartlett’s球形檢驗<0.001，表明數據樣本非常適合進行因素分析．偏度與峰度分析發現，所有條目的偏度與峰度系數都<2，因此，采用ML估計是合適的，為了獲得更穩健的參數估計結果，采用穩健極大似然估計MLR估計．另外，從理論角度以及前人研究結果[3，6]來看，學習興趣幾個因子之間存在較大的相關，因此，選擇斜交旋轉法．雖然許多人在因素分析時，將特征值大于1作為抽取因子的依據，但相關研究證實，當變量數超過40時，采用特征值大于1的方法會造成高估因子數目的情況[19]．平行分析結合碎石圖被認為是探索性因素分析中因子保留最精確的方法[20]．研究采用平行分析法結合碎石圖來決定抽取因子的個數．平行分析發現從模擬的隨機數據中抽取的前3個因子的特征值1.861、1.771、1.706小于實際數據中抽取的前3個因子的特征值22.633、2.554、2.057，從模擬的隨機數據中抽取的第4個因子的特征值為1.651，大于實際數據中抽取的第4個因子的特征值1.491，從碎石圖上也可以看到第3個因子處出現明顯的拐點，因此，決定抽取3個因子．依據因子載荷≥0.45，交叉載荷<0.30，以及在非歸屬因子上載荷<0.25，每個因子條目基本相當的原則保留條目．經過3次旋轉，最終形成的問卷含3個因子，共18個條目．3個因子的累計方差貢獻率為62.16%．

根據問卷編制時的理論構想與3個因子具體條目內容，將5個條目的因子1命名為激發的情境興趣（SI1），6個條目的因子2命名為維持的情境興趣（SI2），7個條目的因子3命名為個體興趣（II）．3個因子具有理想的中度相關（相關系數在0.50~0.70之間），所有條目在其歸屬的因子上的載荷都大于0.55（見表1）．

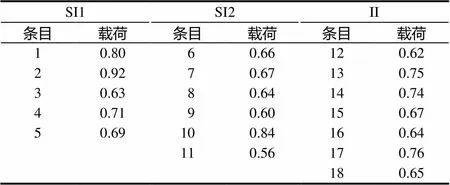
表1 初中生學習興趣問卷18個條目載荷

2.4 驗證性因素分析

運用18個條目的再測問卷對B中學每個初中年級16個班中隨機抽取的3個初一班、2個初二班、2個初三班，共計272名初中生進行調查，經對偶檢測后保留258人，有效率94.85%，其中初一114人、初二72人、初三72人，男生133人、女生125人．使用再測數據，運用Mplus4.2對3因子18條目的結構模型進行驗證，結果發現擬合指數較為理想（見表2 CFA18），為了進一步改善擬合指數，根據Mplus報告的修正指數，刪除SI2中與第6題重疊的第7題(y7 with y6 M.I.=43.863)，各項擬合指數有了進一步的改善（見表2 CFA17）．

表2 初中生數學學習興趣量表驗證性因素分析各項擬合指數

2.5 信效度檢驗

采用內部一致性方法對問卷的信度進行分析．總問卷的Cronbach’s Alpha系數為0.915，3個因子的系數依次為0.854、0.809、0.910，表明初中生數學學習興趣問卷具有良好的穩定性．

初中生數學學習興趣預測問卷在前人研究理論的基礎上提出問卷維度的初步構想，問卷結構和條目測查方法參考了國內外大量研究文獻，在具體條目上，聽取了心理學專家以及心理學研究生、初中一線教師的意見以及5名初中生被試當場作答的反饋意見，反復增刪、修改而成，因此，該問卷具有良好的內容效度．

3 初中生數學學習興趣現狀調查

初中生數學學習興趣正式問卷共17個條目，各條目均采用5點計分（1=非常不符合，5=非常符合），反向條目反向計分，得分越高學習興趣越高．學習興趣水平根據各分量表平均分，分為無興趣（≤<2）、興趣不穩定（2≤<3）、感興趣（3≤<4）、很感興趣（4≤≤5）4種水平（為條目數）．采用“初中生數學學習興趣問卷”對588名初中生進行問卷調查，運用SPSS19.0進行統計檢驗．588名被試330名來自A中學、258名來自B中學．A中學是市屬公辦完全中學，代表一般初中；B中學是一所純初中學校，地處中國科技城——四川省綿陽市腹心地帶，是綿陽市涪城名校，國家基礎教育實驗中心外語實驗學校、國家教育部人文社科項目實驗學校，代表較好的初中．擬通過具有代表性的兩所學校學生數學學習興趣的比較，較為全面地了解初中生數學學習興趣現狀．

3.1 初中生數學學習興趣水平

從表3可見，從3個分量表與總量表平均分來看，588名初中生SI1、SI2與LI都處于感興趣水平，II處于興趣不穩定水平．將感興趣與很感興趣人數百分比相加發現，具有SI1、SI2與II的學生人數百分比依次為：84.35%、76.53%、46.43%．以正態分布曲線下各學習興趣水平（各占1.5個標準差）人數為理論數據，進行頻數分布正態性的檢驗，結果發現，SI1、SI2呈正偏態分布，II呈負偏態分布，且相較于正態分布，無II的學生比例很高、具有II的學生比例很低．

3.2 初中生數學學習興趣的校際差異

從表4可見，B中學初中生SI1、SI2與LI顯著高于A中學，但II差異不顯著．

3.3 初中生數學學習興趣年級差異

從表5可見，588名初中生SI1與SI2存在顯著的年級組間差異，II組間差異不顯著．從表6可見，兩所學校分別進行的年級間差異比較發現：A中學學生在3個分量表上都存在非常顯著的年級組間差異，事后兩兩比較發現初二年級在3個分量表上都顯著低于一三年級，而一三年級只有SI1存在顯著差異；B中學的3個分量表都不存在年級組間差異，事后兩兩比較發現只有初三年級SI2顯著低于一二年級．

表3 588名初中生數學學習興趣平均數和標準差及各水平人數/百分比與正態分布檢驗

注：SI1、SI2、II、LI題目數即依次為5、5、7、17；卡方檢驗時=3，(0.05)=7.81，(0.01)=11.34；*<0.05，**<0.01，后同

表4 初中生數學學習興趣校際差異

注：A中學330人，B中學258人，后同

表5 588名初中生數學學習興趣年級差異

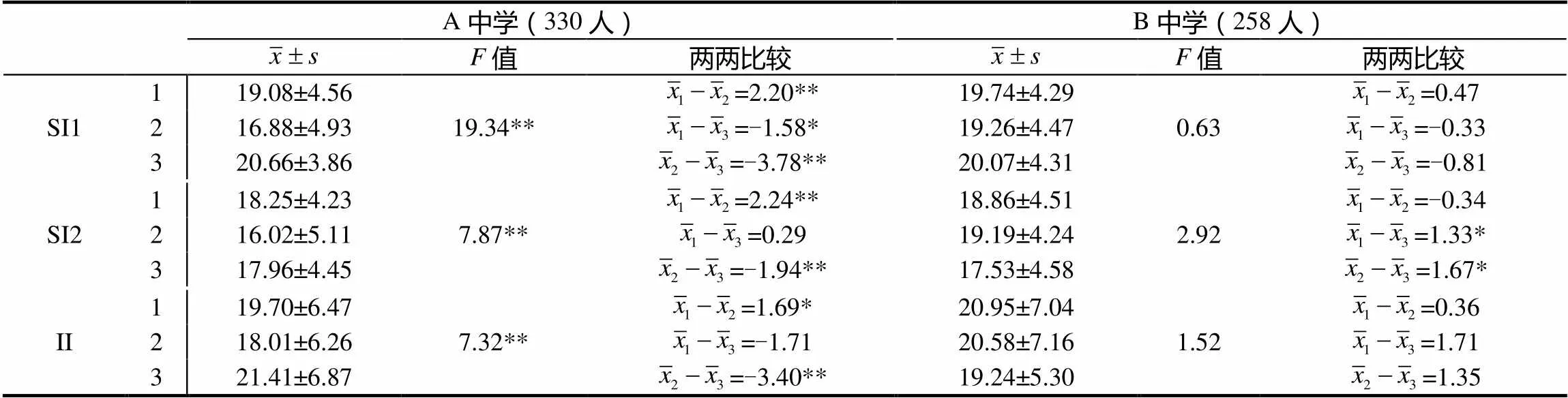
表6 A中學330名被試與B中學258名被試數學學習興趣年級差異

注：A中學初一114人，初二116人，初三100人；B中學初一114人，初二72人，初三72人

3.4 初中生數學學習興趣班際差異

方差分析發現，兩所學校學生3個分量表都存在顯著的班際組間差異，進一步進行同一學校同一年級平行班差異的兩兩比較發現，B中學同一教師任教的兩個初一班3個分量表不存在任何差異，A中學同一教師任教的兩個初三班只有SI2上存在差異．

4 討 論

4.1 初中生數學學習興趣問卷的編制

研究驗證了Hidi和Renninger學習興趣四階段理論的跨文化適應性，同時體現出了中國特色．即該研究得到的學習興趣的一階3因子模型既反應了情境興趣與個體興趣的區別，也反應了情境興趣的兩個階段——激發的情境興趣與維持的情境興趣，同時，相較于Mitchell[3]的二層次模型更為簡潔、更好把握，也更符合中國人的思維與認識，即學習興趣始于激發的情境興趣，最后發展為個體興趣，維持的情境興趣是二者的橋梁與中介．3因子模型也證實了初現的個體興趣與成熟的個體興趣只是量上的差異而無質上差異的猜測，二者應該可以通過個體興趣分量表上分值的高低予以區分，具體區分的分數界限還有待在后續研究中探索確定．

研究依據已有的學習興趣結構理論，在廣泛查閱資料與訪談基礎上編制問卷條目，并對問卷條目進行反復考查和修訂，形成預試問卷，因而，問卷具有良好的內容效度．驗證性因子分析發現，探索性因素結構模型的擬合指數良好，各因子具有理想的中度相關，表明問卷具有較好的結構效度．信度檢驗結果顯示，問卷具有良好的內部一致性信度．可見，該研究所編制的初中生數學學習興趣問卷結構清晰、簡單明了，具有理想的效度與信度以及較強的鑒別與診斷能力．

4.2 初中生數學學習興趣現狀

4.2.1 初中生數學情境興趣尚可

研究發現，中國初中生數學SI1與SI2各水平人數呈正偏態分布，分別有84.35%與76.53%的學生具有SI1與SI2．這表明，當前中國初中生數學情境興趣尚可．但是，情境興趣是短暫的、表淺的，是外部激發與外部維持的，穩定持久、內部激發、自我發動的個體興趣才是學習興趣培養的最終目的所在．該研究調查的兩所學校學生的SI1與SI2均分都還僅處于感興趣水平，根據Hidi與Renninger（2006）[7]的觀點，只有持久濃厚的前一階段的學習興趣才可能向后一階段發展，因此，中國初中數學課堂教學還需進一步提高學生的SI1與SI2．

4.2.2 初中生數學個體興趣亟待提高

研究發現初中生數學II均分處于興趣不穩定水平，各水平學生人數呈負偏態分布，只有46.43%的學生具有II，而且這種低下的II只存在一定的班際差異而不存在校際差異，也不存在初三年級與初一年級的差異．這表明中國初中生數學II普遍低下，更為糟糕的是初中三年對學生II的培養沒有起到任何促進作用．

烏克蘭教育家蘇霍姆林斯基說：“如果一個學生到十二三歲時還沒有興趣愛好，做老師的要為他擔憂，擔心他長大以后對任何事情漠不關心，成為一個平平庸庸的人．”初中階段是學生學習興趣基本形成的階段，如果一個學生在初中階段還沒有形成學習興趣，則其以后的發展就會受到很大的影響．因此，中國初中生數學個體興趣亟待提高．

4.3 初中生數學學習興趣影響因素的分析

4.3.1 學校教學條件與教育理念影響初中生數學學習興趣

研究發現，B中學初中生數學情境興趣（包括SI1與SI2）顯著高于A中學．B中學是一所辦學條件較好、辦學理念較為先進的純初中，青年教師較多，教師在課堂教學中更多地采用了多媒體教學與小組合作的教學方式，師生互動、生生互動較多；另外，相比于A中學，B中學班級規模更小（一個班學生45人左右，而A中學則在60人以上），更有利于教師一對一的輔導．因此，B中學學生數學情境興趣更高．

研究還發現，A中學初二年級學生在各個分量表上得分都最低，這符合人們所說的“初二現象”．即初二學生處于身心巨變、心理斷乳最危險的時期，逆反心理最重、最難管理，最容易出現早戀、上網、成績下滑等問題，容易對學習失去興趣．但這種現象在B中學并不存在，這說明，“初二現象”可能存在，但是遠不如人們所說的那么嚴重，或者說這種“初二現象”通過合理的教育是可以避免的．

4.3.2 教師素質是影響初中生數學學習興趣最為重要的因素

研究發現，初中生數學學習興趣存在顯著的班際差異，但是B中學同一教師任教的兩個初一班不存在任何差異，A中學同一老師任教的兩個初三班差異甚微，出現入學時數學基礎更差的班SI2顯著高于基礎更好的班、II達到感興趣水平（3*7≤22.00<4*7）的反常現象（其他年級均是好班學習興趣高于差班，II處于興趣不穩定水平）．A中學同時任教初三兩個班的老師是公認的好老師，這兩個班的SI1都達到了很感興趣水平（4*5≤20.66<5*5），II總均分達到了感興趣水平（3*7≤21.41<4*7）．可見，教師才是學生學習興趣最重要的影響因素．史炳星從多年數學教師的經驗出發，認為相當一部分孩子從喜歡數學到不喜歡數學，很大成分歸結為數學教育觀念、教學方法和評估方法不重視、愛護和培養學生的學習興趣，不能經常讓學生自己動手學習和盡可能地使數學聯系實際[21]．

5 結 論

（1）初中生數學學習興趣問卷的結構由激發的情境興趣、維持的情境興趣與個體興趣3個因子構成；初中生數學學習興趣問卷具有良好的信效度，且3因素結構模型具有良好的擬合度，說明初中生數學學習興趣問卷適合作為初中生數學學習興趣的測量工具．

（2）中國初中生數學情境興趣有待進一步提高，個體興趣亟需提高．

（3）學校教學理念與教學條件，特別是教師，是影響初中生數學學習興趣最為重要的因素．

[1] Andreas Krapp. Basic Needs and the Development of Interest and Intrinsic Motivational Orientations [J]., 2005, 15(5): 381-395.

[2] Edward L Deci, Richard M Ryan. The “What” and “Why” of Goal pursuits: Human Needs and the Self-Determination of Behavior [J]., 2000, 11(4): 227-268.

[3] Mitchell Matthew. Situational Interest: Its Multifaceted Structure in the Secondary School Mathematics Classroom [J]., 1993, 85(3): 424-436.

[4] Deci E L. The Relation of Interest to the Motivation of Behavior: A Self-Determination Theory Perspective [A]. In: Renninger K A, Hidi S, Krapp A.[C]. Hillsdale, NJ: Lawrence Erlbaum Associates, Inc., 1992.

[5] Chen A, Darst P W, Pangrazi R P. What Constitutes Situational Interest? Validating a Construct in Physical Education [J]., 1999, 3(3): 157-180.

[6] Lisa L G, Amanda M D, Anne M C, et al. Measuring Situational Interest in Academic domains [J]., 2010, 70(4): 1-25.

[7] Hidi S, Renninger K A. The Four-Phase Model of Interest Development [J]., 2006, 41(2): 111-127.

[8] Renninger K A, Wozniak R H. Effect of Interest on Attention Shift, Recognition, and Recall in Young Children [J]., 1985, 21(4): 624-632.

[9] Renninger K A, Ewen L, Lasher A K. Individual Interest as Context in Expository Text and Mathematical Word Problems [J]., 2002, 12(4): 467-491.

[10] ?Harackiewicz J M, Barron K E, Tauer J M, et al. Predicting Success in College: A Longitudinal Study of Achievement Goals and Ability Measures as Predictors of Interest and Performance from Freshman Year Through Graduation [J]., 2002, 94(3): 562-575.

[11] ?Hidi S, Baird W. Strategies for Increasing Text-Based Interest and Students’ Recall of Expository Texts [J]., 1998, 23(4): 465-483.

[12] ?Hidi S. Interest and Its Contribution as a Mental Resource for Learning [J]., 1990，60(4): 549-571.

[13] 房之華．以非智力因素促進學生智力和能力的發展[J]．數學教育學報，1999，8（3）：34-37．

[14] 顏中玉．非智力因素對高師數學學習影響的調查[J]．數學教育學報，2001，10（2）：44-47．

[15] 李如．非智力因素對高職類文科生高等數學學習效果的影響[J]．數學教育學報，2006，15（4）：76-78．

[16] 王光明，宋金錦，王兆云．高中生數學學習非智力特征調查問卷的編制[J]．數學教育學報，2015，24（3）：17-27．

[17] 焦彩珍．初中生數學學習興趣及自我效能與數學學業成績的關系[J]．數學教育學報，2008，17（2）：44-46．

[18] 戴風明，姚林．農村初中數學學困生情意特征的調查研究[J]．數學教育學報，2001，10（4）：96-99．

[19] 吳明隆．問卷統計分析實務——SPSS操作與應用[M]．重慶：重慶大學出版社，2010．

[20] 王孟成．潛變量建模與Mplus應用（基礎篇）[M]．重慶：重慶大學出版社，2014．

[21] 史炳星．談對學生數學學習興趣的愛護和培養[J]．數學教育學報，1999，8（2）：94-97．

附錄：初中生數學學習興趣正式問卷

初中生數學學習興趣問卷

(Junior High School Students’ Mathematics Learning Interest Questionnaire, JHSSMLIQ)

因子項目 激發的情境興趣1. 數學老師有趣． 2. 數學課堂氣氛輕松愉快． 3. 數學課有趣． 4. 數學課堂氣氛單調沉悶． 5. 數學課堂氣氛和諧融洽． 維持的情境興趣6. 數學課上，我容易走神． 7. 我學習數學需要別人的督促． 8. 碰到數學難題我會放棄． 9. 我對數學公式與定理不熟悉． 10. 我學習數學就是為了考試． 個體興趣11. 我喜歡探究數學公式與原理的來龍去脈． 12. 我喜歡不斷嘗試新的、更有效的學習與研究數學的方法與策略． 13. 如果有數學競賽活動，我會主動報名參加． 14. 談起數學的相關知識，我才思如泉涌，口若懸河、滔滔不絕． 15. 偉大的數學家是我奮斗的榜樣． 16. 我喜歡做數學難題． 17. 我以后想從事與數學相關的職業．

[責任編校：周學智]

Development of Mathematics Learning Interest Questionnaire and the Investigation on Junior High School Students

WU Hong-Yan1, LIU Xiao-lin2

(1. School of Education, Neijiang Normal University, Sichuan Neijiang 641100, China;2. Longchang No.1 Middle School, Sichuan Neijiang 642150, China)

Based on the four-phase model of learning interest, we developed a mathematics learning interest questionnaire on junior high school students. Including 17 items and three factors called triggered situational interest (SI1), maintained situational interest (SI2) and individual interest (II) We put it into use and found that: (1) The SI1 and SI2 are acceptable；The II is inferior. (2) There’s significant difference in schools, grades and classes of SI1 and SI2. And there is no significant difference in schools and grades of II. (3) School teaching philosophy and teaching conditions, especially teachers, are the most important reasons for the junior middle school students’ interest in mathematics learning.

junior high school students; mathematics learning interest; the development of questionnaire; survey; cause analysis；education suggestions

G632.0

A

1004–9894（2017）02–0050–05

2016–12–18

吳洪艷（1973—），女，貴州雷山人，副教授，碩士，主要從事教育與心理應用研究．