創(chuàng)設數(shù)學靈動課堂策略探尋

摘 要：介紹創(chuàng)設數(shù)學靈動課堂的四種策略：利用數(shù)學魔術(shù)、數(shù)學卡通、數(shù)學謎語、數(shù)學思維導圖的策略.并將這些策略實施于課堂教學之中，激發(fā)學生學習數(shù)學的興趣，使得課堂更加生活活潑，靈動.

關(guān)鍵詞：靈動課堂；策略；創(chuàng)設

數(shù)學由于本身特有的高度抽象性，容易抹殺學生對數(shù)學學習的興趣.[1 ]在數(shù)學課堂中，教師通過各種媒體渠道將信息與時俱進地融入到課堂教學中，通過淡化形式、注重實質(zhì)，使得課堂顯得靈動.比如數(shù)學魔術(shù)、數(shù)學卡通、數(shù)學謎語、數(shù)學思維導圖等等，只要授課之時適時加以靈活應用，便更可激發(fā)學生學習的積極性，使課堂靈動，筆者對此深有體會，特提出與同行分享.

1 策略一 數(shù)學魔術(shù)

魔術(shù)又稱障眼法，是以特殊的技巧跟設備，營造錯覺和認知偏誤，以娛樂觀眾，使他們覺得不可思議的表演藝術(shù).而數(shù)學魔術(shù)是通過娛樂學生，使學生在各種他們認為“偶然”的現(xiàn)象中尋找“必然”，發(fā)現(xiàn)出隱含的數(shù)學規(guī)律，從而使學生對數(shù)學的認知更加深刻.

案例1：魔術(shù)表演：找撲克牌——百發(fā)百中：

（1）一疊撲克牌打亂，花色朝向?qū)W生，學生任意指定抽取一張；

（2）教師將學生指定的牌展示給觀眾，讓全體學生記住花色和數(shù)值（教師看不到）；

（3）教師將學生抽出的牌插回洗牌；

（4）學生再次洗牌；

（5）教師準確無誤地找出原先學生指定的那張牌。

通過百發(fā)百中的猜牌游戲，學生的好奇心被激發(fā)，都想知道該魔術(shù)的奧秘，教師趁勢提出如下問題：

問題1：從數(shù)學的角度看，這付牌有什么共同特征；

問題2：教師在哪個地方做了手腳？

謎底揭曉：1.數(shù)只有奇數(shù).

2.花色中沒有方塊.

3.圖案是具有方向性.

4.教師抽出的那張牌放回時被顛倒了。這張牌和整體是唯一方向不同的！

這個游戲作為學生的開學第一課或者是講解圖形對稱性時都是絕妙好招.因為學生很想知道這個魔術(shù)是怎樣產(chǎn)生，注意力精力集中自然不在話下，教師讓學生觀察，將抽出的那張牌通過實物投影給大家看，最后將手上的牌給大家看，學生通過仔細地觀察，引導和同伴交流，發(fā)現(xiàn)和探索、歸納出魔術(shù)的原理，從中發(fā)現(xiàn)出必然的規(guī)律這就是學好數(shù)學的八字真經(jīng)：觀察、發(fā)現(xiàn)、探索、歸納。數(shù)學魔術(shù)的本質(zhì)就是一種數(shù)學實驗，通過實驗的方式使得學生能獲得相應的數(shù)學活動經(jīng)驗.

2 策略二 數(shù)學卡通

卡通是指利用視覺的藝術(shù)創(chuàng)作一種幽默的體驗。由于它的直觀性，深受觀眾特別是小孩子的喜愛.如果我們在數(shù)學中能將一些卡通滲透入教學中，將使得課堂熠熠生輝.

案例2：比較3■ 和2■的大小.

方法1.平方法，將兩個數(shù)分別平方轉(zhuǎn)化為整數(shù)后比較大小，以此推斷原數(shù)的大小.

方法2.將3■化為■，2■化為■，然后通過比較被開方數(shù)大小，再比較兩個原數(shù)大小.

在教學時再滲透加入了卡通（如圖1），引發(fā)學生的笑聲，起到了很好的教學效果.

案例3：二次函數(shù)的頂點

我們知道，二次函數(shù)的頂點式能幫我們快速表象出函數(shù)的圖像，也是體現(xiàn)函數(shù)“幾何直觀”的重要表現(xiàn)形式.同時頂點在函數(shù)的左右上下平移中起到了決定性作用.老師常常強調(diào)二次函數(shù)頂點式中頂點的重要性.為了能給學生以震撼的效果，可以采用下列的卡通（見圖2），這樣的展示可使學生的印象特別的深刻，特別有利于記憶.

再如：案例4：正方形

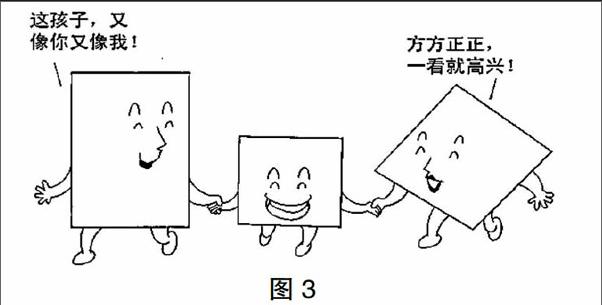
教師在講解正方形的性質(zhì)和判斷時通常要強調(diào)正方形具有矩形和正方形的所有性質(zhì)，在證明四邊形是正方形時經(jīng)常是要先引導學生證明它是菱形，然后再證明它是矩形，進而再說明它是正方形.可是有些學生要么漏掉某些證明步驟，要么所有條件雜糅在一起證明它是一個正方形.教師展示如下卡通（如圖3），矩形和菱形作為“父母”，正方形作為“孩子”，正方形遺傳了菱形和矩形的“基因”—即所有的性質(zhì).

教師通過展示卡通形象，讓學生對學習數(shù)學充滿期待.數(shù)學好玩的念頭在心中升起.

3 策略三 數(shù)學謎語

案例5：數(shù)學老師在上完《移項》這節(jié)課末，讓學生猜一個謎語：

霸王別姬（打一數(shù)學名詞）

引導學生通過聯(lián)想虞姬和項羽的愛情故事，知道“虞”和“項”，進而猜出就是今天學習的數(shù)學內(nèi)容”移項“。多年后學生對這節(jié)課還是記憶猶新，對老師的睿智，思維的豐富性會由衷嘆服.

案例6：

師：現(xiàn)在我們一起來猜謎，知道的同學來說一說.（出示幻燈片）

①我盼著你，你盼著我.（打一數(shù)學名詞）

②我先走了.（打一數(shù)學名詞）

生1：互盼.

生2：對等.

師：生1的說法快接近答案了，可惜還違背了謎底、謎面字不能相沖的原則.生2的同學很不錯了.還有別的想法嗎？

生3：第②個謎我猜是不等.

師：你是如何想的？能否告訴同學們一下？

生3：我先走了，說明不再等了，所以謎底是不等.

師：解釋得真好，大家能否從剛剛這同學的想法中得到啟發(fā).

生4：我知道了，第①個謎底是：相等，意思是我等著你來，你也等著我來，就是相互等待，謎底相等.

師：看來同學們真不錯.（此時上課鈴響）

師：我們剛剛從猜謎中獲得了兩個謎底，一是相等，一個是不等。其實我們生活實際也經(jīng)常由這兩類問題構(gòu)成。在我們數(shù)學上，相等時你想到什么數(shù)學知識，不等時想到什么數(shù)學知識？

生（眾）：相等想到方程，不等想到不等式.

師：恩，真聰明！那我再問大家一個問題，在解方程和不等式中，你們喜歡什么？

生（眾）方程！

師：異口同聲，沒經(jīng)過商量吧！（學生笑），這位同學來告訴我為什么？

生5：不等式還要考慮變號，有點討厭！

師：我也是這么認為的。握手，英雄所見略同呀！（生笑） [2 ]

這是筆者借班上課時用猜謎引入的開場白，使得學生在由不熟悉的老師授課和有眾多老師聽課的情況下不會感到緊張，從而保證課堂教學的順利進行.特級教師任勇在上課時也喜歡將謎語滲透到數(shù)學教學當中.如利用方程思想猜一個字，謎面：人有它大，天無它大.謎底是“一”.這些舉措使得數(shù)學課堂氣象萬千，顯得更加大氣.

4 策略四 數(shù)學思維導圖

數(shù)學思維導圖是模擬大腦的樹突結(jié)構(gòu)，圖文并重的技巧，把各級主題的關(guān)系用相互隸屬與相關(guān)的層級圖表現(xiàn)出來，把主題關(guān)鍵詞與圖像、顏色等建立記憶鏈接，思維導圖充分運用左右腦的機能，利用記憶、閱讀、思維的規(guī)律，協(xié)助人們在科學與藝術(shù)、邏輯與想象之間平衡發(fā)展，一定程度做到了思維的可視化的效果，其中知識樹將是思維導圖的很好的呈現(xiàn)形式.

案例7：數(shù)學廊道

圖4是經(jīng)筆者收集整理改編后做成展板的形式放在我校的數(shù)學廊道.將初中所學數(shù)學知識的橫向和縱向聯(lián)系在一起，相當于初中數(shù)學知識的一張地圖.只要學生用心揣摩，必定會有收獲.每次來自臺灣、新加坡的學校到訪，都對這個廊道表現(xiàn)出濃厚的興趣.

案例：

案例8：《圓》復習課知識樹

復習課對知識的梳理、理清各個知識點的邏輯關(guān)系是十分重要的.筆者在復習課前一天以導學案的形式讓學生對《圓》這章進行整理。讓學生有時間進行充分的思考，利用知識樹的形式顯現(xiàn)出來（如圖5）.筆者再將其中的“優(yōu)秀作品”利用實物投影進行展示、交流、欣賞，造型各異的的樹立馬引起學生的注意力，也營造了輕松愉快的學習氣氛，同時也讓學生對本章的內(nèi)容框架有了更深的體會.

記得孫維剛老師說過，學習數(shù)學要”八方聯(lián)系，魚翔淺底“，對數(shù)學而言，能夠以數(shù)學的眼光去觀察、理解現(xiàn)實世界，為我所用。只要我們抓住”魚“——數(shù)學這個本質(zhì)，那么對數(shù)學教學將成為匯聚各方小流的一條大河，數(shù)學老師將是那一條永不干涸的河水.利用學生的各種好奇心，使得課堂靈動起來，讓數(shù)學的氣象有萬種風情，課堂變成學習展示、分享、交流的平臺.

參考文獻：

[1]任勇.期盼數(shù)學氣象萬千[J].數(shù)學通報，2011（9）：45-50.

[1]陳海烽.讓學生的思維飛一會兒[J].中小學數(shù)學，2015（1-2）：117-11.

[2]陳海烽.用課堂語言激發(fā)學生學習的正能量[J].初中數(shù)學教與學，2015（1）：3-5.