基于矩陣運(yùn)算K短路徑算法

趙禮峰，黃奕雯

(南京郵電大學(xué) 理學(xué)院，江蘇 南京 210046)

基于矩陣運(yùn)算K短路徑算法

趙禮峰，黃奕雯

(南京郵電大學(xué) 理學(xué)院，江蘇 南京 210046)

最短路問(wèn)題是復(fù)雜網(wǎng)絡(luò)中的經(jīng)典問(wèn)題，其求解算法層出不窮，各有優(yōu)缺點(diǎn)。經(jīng)典的算法包括Dijkstra算法、Ford算法和Floyd算法等，只能求解兩節(jié)點(diǎn)間的一條最短路徑。在實(shí)際生活中，還需要在大型網(wǎng)絡(luò)中限定一些前提條件求解兩點(diǎn)間次短、漸次短的路徑問(wèn)題。為此，提出了一種對(duì)距離矩陣和路徑矩陣的迭代、替換算法，即從一個(gè)節(jié)點(diǎn)出發(fā)尋找其后繼節(jié)點(diǎn)，同時(shí)通過(guò)比較路徑長(zhǎng)短得到兩點(diǎn)間最短路徑、次短路徑和漸次短路徑，并不斷重復(fù)、替換。為驗(yàn)證所提算法的有效性，以一個(gè)大型網(wǎng)絡(luò)的應(yīng)用作為實(shí)例，應(yīng)用Matlab對(duì)所提算法進(jìn)行了仿真實(shí)驗(yàn)驗(yàn)證。仿真結(jié)果表明，所提算法能夠在復(fù)雜大規(guī)模隨機(jī)網(wǎng)絡(luò)中滿足求解指定頂點(diǎn)間最短、次短和漸次短路徑的需要，具有較好的有效性和適用性。

次短路徑；漸次短路徑；距離矩陣；路徑矩陣

0 引 言

最短路徑問(wèn)題是復(fù)雜網(wǎng)絡(luò)中一大經(jīng)典問(wèn)題，它的應(yīng)用領(lǐng)域十分廣泛，如通信網(wǎng)絡(luò)、物流運(yùn)輸、地理信息系統(tǒng)、軍事運(yùn)籌學(xué)和旅行規(guī)劃等等[1]。經(jīng)典算法[2]卻只能解決兩節(jié)點(diǎn)間一條最短路，而在這些實(shí)際運(yùn)用中，往往不僅僅考慮一條最短路徑，還要根據(jù)實(shí)際情況及具體要求選擇其次短路徑、漸次短路徑。比如說(shuō)在旅行線路的規(guī)劃問(wèn)題上，所要選擇的路線不一定是距離最短的路線，還要考慮實(shí)際路況、天氣、經(jīng)濟(jì)效益等因素，那么就需要篩選出不止一條短路徑。

對(duì)于K短路徑問(wèn)題，國(guó)內(nèi)外學(xué)者們已經(jīng)取得了一些研究成果。例如，Eppstein給出了一個(gè)允許有向圖上的路徑環(huán)存在的算法[3]；陳文蘭等提出了一種求解次短和漸次短路徑的實(shí)用算法[4]；Yen提出了一種無(wú)環(huán)的K短路算法[5]，趙見在他的基礎(chǔ)上提出了求解無(wú)環(huán)K短路徑的Dijkstra算法[6]；柴登峰[7]、牛新奇[8]等通過(guò)刪去最短路中某些邊以及邊對(duì)得到新的子圖，再?gòu)淖訄D中求得最短路，然后通過(guò)排序的方法得到前K條短路徑。之后，王文寧提出了基于優(yōu)化的Floyed算法前r條最短路徑的實(shí)現(xiàn)[9]。

在之前算法的基礎(chǔ)上，又由Floyed的算法特性得出了任意節(jié)點(diǎn)間最短路、次短路以及漸次短路的路長(zhǎng)，但是無(wú)法得出具體路徑。

為此，在研究上述算法的基礎(chǔ)上，提出了距離矩陣和路徑矩陣的迭代、替換算法，通過(guò)矩陣計(jì)算最短、次短、漸次短路徑問(wèn)題。理論分析和仿真實(shí)驗(yàn)結(jié)果均表明：該算法簡(jiǎn)便有效、實(shí)用性較強(qiáng)，適用于大型復(fù)雜網(wǎng)絡(luò)的求解。

1 相關(guān)知識(shí)

定義1[6,10]前K條最短路徑問(wèn)題：設(shè)有賦權(quán)圖G(V,E)及其上給定的兩個(gè)頂點(diǎn)vi和vj,r為vi和vj之間的一條路徑,記其長(zhǎng)度為d(r),由vi和vj之間的所有互不相同的路徑組成的集合R(G,vi,vj)稱為G上vi和vj之間的路徑集合,即R(G,vi,vj)={r|r為G上vi,vj之間的路徑}。若按路徑長(zhǎng)度值大小將其排列得r1,r2,…,rM,d(r1)≤d(r2)…≤d(rM),則稱r1為G上vi和vj間的第1最短路徑(即狹義最短路徑),d1為其長(zhǎng)度;r2為G上vi和vj間第2最短路徑,d2為其長(zhǎng)度;rM為G上vi和vj間第M最短路徑,dM為其長(zhǎng)度。求取G上vi和vj間的第1～K(K≤M)最短路徑的問(wèn)題稱為前K條最短路徑問(wèn)題。

定義2 最短路徑：K=1時(shí)的K短路徑，記作PF。

定義3 次短路徑：K=2時(shí)的K短路徑，記作PS。

定義4 漸次短路徑：K=3時(shí)的K短路徑，記作PT。

定義5 距離矩陣T：在n個(gè)節(jié)點(diǎn)的網(wǎng)絡(luò)G(V,E,1)中，距離矩陣T=(tij)n×3。其中，ti0為節(jié)點(diǎn)vi到其他各節(jié)點(diǎn)的最短路徑長(zhǎng)；ti1為節(jié)點(diǎn)vi到其他各節(jié)點(diǎn)的次短路徑長(zhǎng)；ti2為節(jié)點(diǎn)vi到其他各節(jié)點(diǎn)的漸次短路徑長(zhǎng)。

定義6 路徑矩陣F：在n個(gè)節(jié)點(diǎn)的網(wǎng)絡(luò)G(V,E,I)中，路徑矩陣F=(fij)n×3,fij為收點(diǎn)的前點(diǎn)標(biāo)號(hào)。

引理1[4]：設(shè)PSij是從頂點(diǎn)vi到頂點(diǎn)vj的次短路徑,對(duì)于任意頂點(diǎn)vk∈PSij,若vk∈PFij,則有：

(1)PFij=PFik∪PFkj;

(2)PSij=PFik∪PSkj或PSik∪PFkj。

若vk?PFij,則PSij=PFik∪PFkj。

引理2[4]：設(shè)PTij是從頂點(diǎn)vi到頂點(diǎn)vj的漸次短路徑,對(duì)于任意頂點(diǎn)vk∈PTij,若vk∈PFij,則有：

(1)PFij=PFik∪PFkj;

(2)PTij=PTik∪Pkj或PFik∪PTkj或PSik∪PSkj。

若vk∈PSij且vk?PFij,則PSij=PFik∪PSkj。若vk?PFij且vk?PSij,則PTij=PFik∪PFkj。

2 算 法

2.1 算法思想

在文獻(xiàn)[4]提出的算法中，由引理1和引理2得知，要求從頂點(diǎn)vi到頂點(diǎn)vj的最短路徑、次短路徑、漸次短路徑，只需要從頂點(diǎn)vi開始，依次對(duì)每個(gè)頂點(diǎn)求它的最短路徑、次短路徑和漸次短路徑，并逐次向后擴(kuò)展，直到達(dá)到目標(biāo)頂點(diǎn)vj，即可求得。文獻(xiàn)[4]首先引入了四組變量：L,T,F,S。每組變量的意義及取值如下：l是對(duì)節(jié)點(diǎn)選擇的標(biāo)記，初始化為(0,0,0)。當(dāng)l=0時(shí)，為臨時(shí)標(biāo)號(hào)；當(dāng)l=1時(shí)，為永久標(biāo)號(hào)。t的取值為每次求出的路徑長(zhǎng)度，初始化為(∞，∞，∞)，從左到右依次為最短路長(zhǎng)、次短路長(zhǎng)和漸次短路長(zhǎng)。f為收點(diǎn)的前點(diǎn)標(biāo)號(hào)，初始化為(-1，-1，-1)，從左到右依次為最短路徑收點(diǎn)的前點(diǎn)標(biāo)號(hào)，次短路徑收點(diǎn)的前點(diǎn)標(biāo)號(hào)和漸次短路徑收點(diǎn)的前點(diǎn)標(biāo)號(hào)。s是對(duì)路徑種類的標(biāo)記，初始化為(-1，-1)。當(dāng)s=0時(shí)，前段路徑為最短路徑；當(dāng)s=1時(shí)，前段路徑為次短路徑；當(dāng)s=2時(shí)，前段路徑為漸次短路徑。

具體算法概述如下：

Step1:初始化。

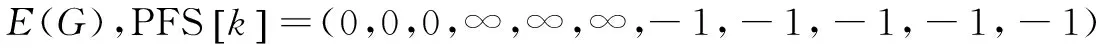
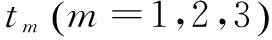
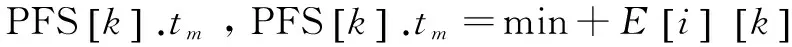
Step4:若min選定的是t1的值，則s=0;選定的是t2的值，則s=1;選定的是t3的值，則s=2。

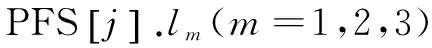
2.2 算法步驟

Step4：令k:=k+1，轉(zhuǎn)到Step2，直到mink=∞時(shí)，結(jié)束。

3 算法復(fù)雜度及合理性分析

3.1 空間復(fù)雜度

該算法在網(wǎng)絡(luò)圖中的存儲(chǔ)結(jié)構(gòu)[11]為兩個(gè)n×3的矩陣—距離矩陣T和路徑矩陣F。因此該算法的空間復(fù)雜度為O(3n+3n)=O(6n)。

3.2 時(shí)間復(fù)雜度

該算法的核心是在每次迭代中尋找最短的一條路徑，次短的一條路徑，漸次短的一條路徑,然后進(jìn)行排列得到其K短路徑。那么每次在距離矩陣T中尋找路程最短的路都要遍歷整個(gè)距離矩陣T，而路徑矩陣F也隨距離矩陣T的變化而變化。其時(shí)間復(fù)雜度為O(3n)，而整個(gè)算法的運(yùn)行需要做3n次循環(huán)，所以總的算法復(fù)雜度為O(3n×3n)=O(n2)。

3.3 合理性分析

基于矩陣運(yùn)算K短路徑算法是基于文獻(xiàn)[4]中的算法在運(yùn)算的存儲(chǔ)結(jié)構(gòu)上的一種改進(jìn)[12]，從而簡(jiǎn)化運(yùn)算同時(shí)節(jié)省了存儲(chǔ)空間，所以原文中的定理即文中的引理可以說(shuō)明次短路和漸次短路求解的正確性。同時(shí)由于該算法中最短路的求解是基于經(jīng)典最短路算法Dijkstra，所以使用該算法無(wú)法解決含有賦權(quán)值的網(wǎng)絡(luò)。

4 應(yīng)用實(shí)例

例題：南京旅游局開通了一條旅行專線[13],途中經(jīng)過(guò)5個(gè)景點(diǎn)(奧體中心、中山陵、夫子廟、中華門、玄武湖)，每班車的發(fā)車時(shí)間固定,如果在某一時(shí)刻出發(fā)從一個(gè)景點(diǎn)到另一個(gè)景點(diǎn),討論不同時(shí)刻出發(fā)去某一景點(diǎn)的最短時(shí)間。

班車時(shí)刻表如表1所示。

表1 班車時(shí)刻表

問(wèn)：(1)某人在11:30要從奧體中心出發(fā)去中山陵游玩，怎樣乘車才能最快到達(dá)？

(2)由于南京道路在節(jié)假日及上下班高峰期時(shí)常發(fā)生擁堵，尤其是第一問(wèn)中求出的最短路中由夫子廟到中山陵這段路，而且最短路線中從奧體中心到中山陵只路過(guò)夫子廟這一個(gè)景點(diǎn)，可參觀地點(diǎn)較少，所以希望再設(shè)計(jì)出從奧體中心到中山陵的次短路徑以及漸次短路徑，這樣既可以參觀更多的景點(diǎn),又可以在發(fā)生大規(guī)模擁堵的情況下可以選擇較為暢通的路線行駛。

解：(1)把換乘旅行班車問(wèn)題運(yùn)用到圖論中轉(zhuǎn)化為最短路問(wèn)題。首先，令?yuàn)W體中心為A點(diǎn)(該例中作為發(fā)點(diǎn))，夫子廟為B點(diǎn)，中華門為C點(diǎn)，玄武湖為D點(diǎn)，中山陵為E點(diǎn)(該例中作為收點(diǎn))，做出旅行班車的路線圖。因?yàn)槁眯邪嘬囃？奎c(diǎn)時(shí)間固定，所以不同的出發(fā)時(shí)間，會(huì)有不同的時(shí)間圖，即圖中邊上的權(quán)值不同。圖1為11:30時(shí)出發(fā)的路線圖，為賦權(quán)無(wú)回路有向圖。

圖1 景點(diǎn)分布圖

任意使用一種最短路問(wèn)題的算法求得從奧體中心(A)到中山陵(E)最快需要90min，路線為：奧體中心(A)→夫子廟(B)→中山陵(E)。

(2)用文中提出的算法首先得到以上賦權(quán)有向圖的距離權(quán)矩陣D：

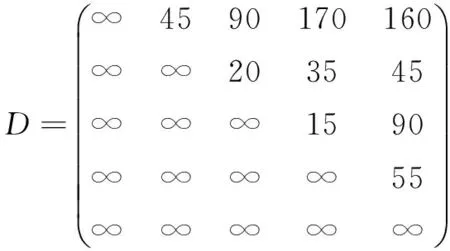
接著初始化距離矩陣和路徑矩陣，根據(jù)算法逐次迭代，計(jì)算過(guò)程如下：

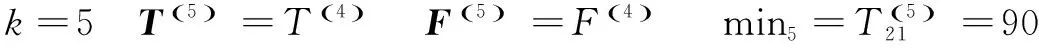
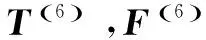
所以，得到結(jié)論如下：

A→B：A→B=45

A→C：A→B→C=65，A→C=90

A→D：A→B→D=80，A→B→C→D=80，A→C→D=105

A→E：A→B→E=90，A→B→D→E=135，A→B→C→D→E=135

可以看到，從奧體中心(A)到中山陵(E)次短路線需要135min，路線為：奧體中心(A)→夫子廟(B)→玄武湖(D)→中山陵(E)；漸次短路線也需要135min，路線為：奧體中心(A)→夫子廟(B)→中華門(C)→玄武湖(D)→中山陵(E)。

從結(jié)論可以看出，如果選擇漸次短路線，那么可以在一天去完所有景點(diǎn)，但如果考慮游覽的時(shí)間，選擇次短路線既可避開擁堵道路，也可以增加一個(gè)景點(diǎn)游玩。

5 算法仿真(摘自2015年研究生數(shù)學(xué)建模F題第一問(wèn))

旅游路線規(guī)劃問(wèn)題：

旅游活動(dòng)正在成為全球經(jīng)濟(jì)發(fā)展的重要?jiǎng)恿χ唬铀倭藝?guó)際資金流轉(zhuǎn)和信息、技術(shù)管理的傳播，創(chuàng)造了高效率的消費(fèi)行為模式、需求和價(jià)值等。隨著國(guó)民經(jīng)濟(jì)的快速發(fā)展，人們生活水平得到很大提升，越來(lái)越多的人開始積極參與有益于身心健康的旅游活動(dòng)。

現(xiàn)有一批自駕游愛好者希望從北京出發(fā)自駕去新疆游玩，沿途可以邊走邊玩。根據(jù)各省會(huì)城市之間公路里程信息，利用上述算法得出前K條短路徑，以便各位自駕游車主選擇適合自己的線路。

由于要求的旅行線路問(wèn)題，是由31個(gè)省作為31個(gè)節(jié)點(diǎn)，省會(huì)間距離作為權(quán)值構(gòu)成的有向賦權(quán)網(wǎng)絡(luò)，大致網(wǎng)絡(luò)圖如圖2所示。這是一個(gè)較為大型的網(wǎng)絡(luò)，數(shù)值計(jì)算較為麻煩，在Matlab[14]中對(duì)該算法進(jìn)行仿真從而得出結(jié)果。

仿真結(jié)果均是在CPU為InterCore(TM)i5-4200M,2.50Hz,內(nèi)存8GB,MATLABR2009b環(huán)境下運(yùn)行實(shí)現(xiàn)的。

部分具體行程表(按路徑長(zhǎng)度生序排列)如表2所示，起點(diǎn)和終點(diǎn)分別為北京和烏魯木齊。路程按照省會(huì)間距離計(jì)算。

由表2可以看出,可以針對(duì)自駕游車主的不同要求為其制定適合的旅行線路：比如，若該自駕游車主需要最快的線路，那么可以為他推薦線路1(最短路線路)；若該自駕游車主希望在旅行中經(jīng)過(guò)石家莊市辦事，可以為他推薦線路2(次短路線路)；若該自駕游車主同時(shí)游覽超過(guò)5個(gè)省，可以為他推薦線路3(漸次短路線路)。

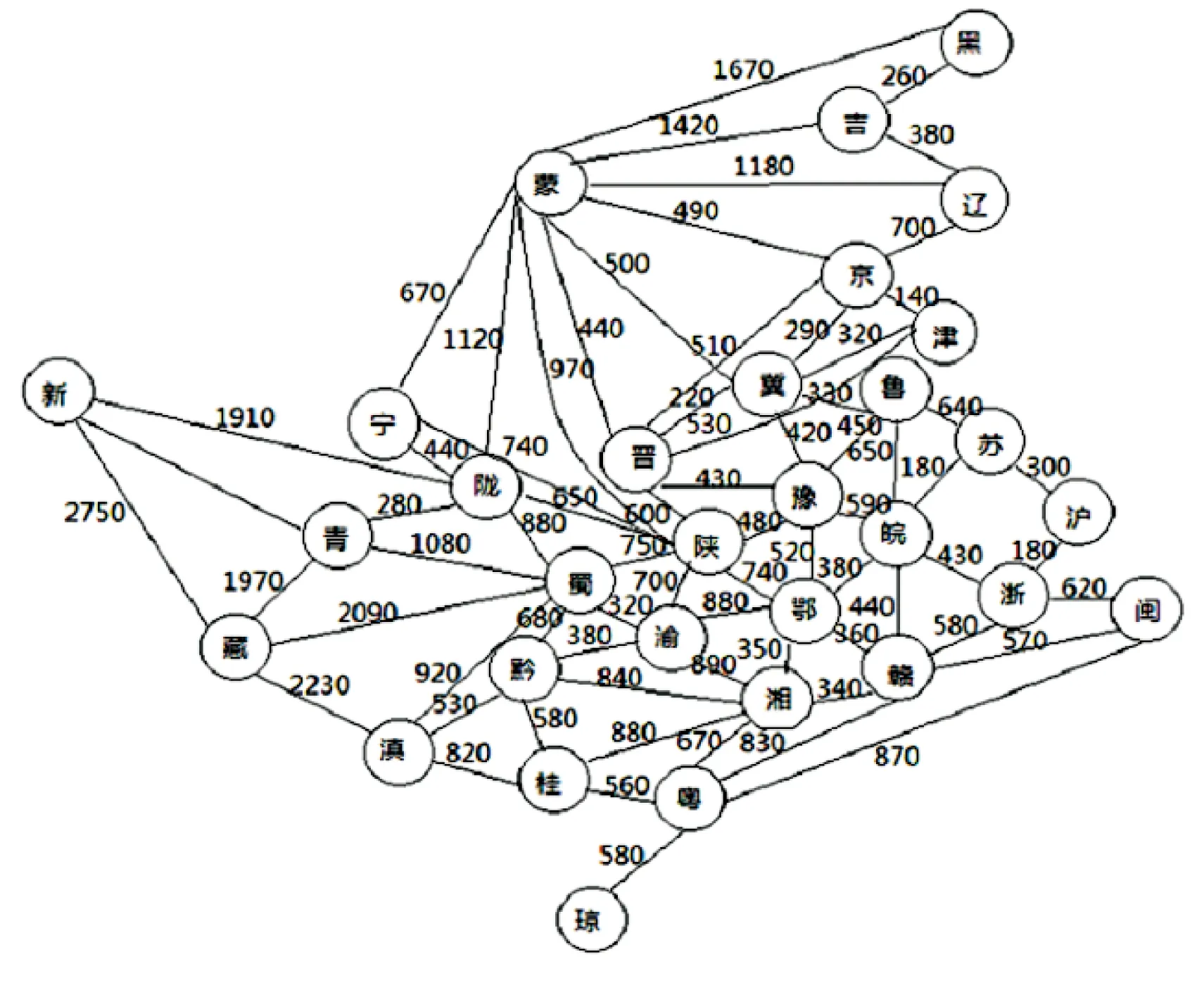
圖2 省間距離圖 表2 具體行程表

線路途經(jīng)省、市總路程/km1(最短路)內(nèi)蒙古呼和浩特市、甘肅省蘭州市35202(次短路)河北省石家莊市、內(nèi)蒙古呼和浩特市、甘肅省蘭州市38203(漸次短路)河北省石家莊市、山西省太原市、內(nèi)蒙古呼和浩特市、甘肅省蘭州市3980

6 結(jié)束語(yǔ)

針對(duì)傳統(tǒng)算法只能解決一條最短路的局限性，提出了一種通過(guò)距離矩陣的迭代操作和路徑矩陣的替換操作得出前K條短路徑的算法。該算法利用矩陣進(jìn)行記錄和計(jì)算，一定程度上簡(jiǎn)化了仿真的復(fù)雜性。在理 論分析的基礎(chǔ)上，進(jìn)行了相關(guān)實(shí)例仿真計(jì)算，以驗(yàn)證該算法的有效性和可行性。理論分析及仿真驗(yàn)證結(jié)果表明，該算法基于Matlab平臺(tái)對(duì)于包括生活中旅行線路選擇問(wèn)題在內(nèi)的大型復(fù)雜網(wǎng)絡(luò)求解具有較好的實(shí)用性。

[1] 謝 政.網(wǎng)絡(luò)算法與復(fù)雜性理論[M].長(zhǎng)沙:國(guó)防科技大學(xué)出版社,2003.

[2] 劉煥淋,陳 勇.通信網(wǎng)圖論及應(yīng)用[M].北京:人民郵電出版社,2010.

[3]EppsteinD.Findingthekshortestpaths[J].SIAMJournalofComputing,1998,28：652-673.

[4] 陳文蘭,潘蔭榮.一個(gè)求解次短和漸次短路徑的實(shí)用算法[J].計(jì)算機(jī)應(yīng)用與軟件,2006,23(1):94-96.

[5]YenJY.Findingthekshortestlooplesspathsinanetwork[J].ManagementScience,1971,17(11):712-716.

[6] 趙 見.求解無(wú)環(huán)K短路徑的Dijkstra算法[J].淮陰師范學(xué)院學(xué)報(bào):自然科學(xué)版,2012,11(1):8-12.

[7] 柴登峰,張登榮.前N條最短路徑問(wèn)題的算法及應(yīng)用[J].浙江大學(xué)學(xué)報(bào):工學(xué)版,2002,36(5):531-534.

[8] 牛新奇,潘蔭榮,胡幼華.K(≤3)條漸次短路徑搜索算法的研究[J].計(jì)算機(jī)工程與應(yīng)用,2005,41(22):51-53.

[9] 王文寧.基于優(yōu)化的Floyed算法前r條最短路徑的實(shí)現(xiàn)[J].常州工學(xué)院學(xué)報(bào),2009,22(5):28-30.

[10]HoffmanW,PavleyR.AmethodofsolutionoftheNthbestpathproblem[J].JournaloftheACM,1959,6(4):506-514.

[11]KatohN,IbarakiT,MineH.Anefficientalgorithmforkshortestsimplepaths[J].Networks,1982(12):411-427.

[12] 高 松,陸 鋒.K則最短路徑算法效率與精度評(píng)估[J].中國(guó)圖象圖形學(xué)報(bào),2009,14(8):1677-1683.

[13] 張國(guó)伍,錢大琳.公共交通線路網(wǎng)多條最短路徑算法[J].系統(tǒng)工程理論與實(shí)踐,1992,23(4):22-26.

[14] 劉衛(wèi)國(guó).MATLAB程序設(shè)計(jì)與應(yīng)用[M].北京:高等教育出版社,2006.

Research onK-shortest Path Algorithm with Matrix Operations

ZHAO Li-feng,HUANG Yi-wen

(College of Mathematics and Physics,Nanjing University of Posts and Telecommunications,Nanjing 210046,China)

Shortest path problem is a classic problem in complex networks,and their solutions after another and all have their advantages and disadvantages.The algorithm of Dijkstra,Ford and Floyd are most classical among these algorithms.However,these algorithms are only for solving a shortest path between nodes.In real life,some limited prerequisites are needed to find the second shortest path and the third shortest path between two nodes in large-scale networks.Therefore,the iterating and displacement algorithm for distance matrix and path matrix is proposed，started from one node to its successor node then compared to find the first shortest path,the second shortest path and the third shortest path repeating and replacing constantly.In order to verify the effectiveness of the proposed algorithm,taking a large network as an example,Matlab is applied to identify it in simulation.It is demonstrated that the proposed algorithm can calculate the first shortest path,the second shortest path and the third shortest path in a complex large-scale random networks,with good validity and applicability.

second shortest path;third shortest path;distance matrix;channel matrix

2016-04-22

2016-08-11

時(shí)間：2017-03-07

國(guó)家自然科學(xué)基金資助項(xiàng)目(61304169)

趙禮峰(1959-),男,教授,碩士研究生導(dǎo)師,研究方向?yàn)閳D論及其在通信中的應(yīng)用;黃奕雯(1991-),女,碩士研究生,研究方向?yàn)閳D論及其在通信中的應(yīng)用。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170307.0920.002.html

TP301.6

A

1673-629X(2017)04-0098-06

10.3969/j.issn.1673-629X.2017.04.022