基于網絡博弈論的謠言擴散建模研究

余莎莎，王友國，朱 亮

(1.南京郵電大學 理學院，江蘇 南京 210046；2.南京郵電大學 通信與信息工程學院，江蘇 南京 210003)

基于網絡博弈論的謠言擴散建模研究

余莎莎1，王友國1，朱 亮2

(1.南京郵電大學 理學院，江蘇 南京 210046；2.南京郵電大學 通信與信息工程學院，江蘇 南京 210003)

隨著網絡技術的不斷發展，在線社交網絡已經成為大眾交互觀點，抒發意見的主流平臺。通過建立謠言擴散模型，研究社交網絡中的謠言傳播機制，為控制謠言傳播提供指導和幫助。社交網絡中，用戶行為決策受其自身利益影響，因此，結合網絡博弈論，給出用戶在社交網絡中選擇傳播謠言或不傳播謠言的概率表達式。在此基礎上，分析謠言在社交網絡中的傳播過程，結合用戶可隨時改變自身決策的行為特點，建立謠言擴散模型。并分別基于無標度網絡和小世界網絡，進行數值仿真，分析用戶決策轉換比例對謠言擴散的影響。實驗結果表明，用戶決策轉換比例中的固有影響因子與時間速率因子對謠言在網絡中的擴散具有顯著影響，隨著決策轉換比例的減小，謠言擴散速率與最終擴散規模將出現不同程度的減小。同時，當風險主導程度足夠小時，無論其如何變化，謠言必定擴散至整個網絡，相反地，對于足夠大的風險主導程度，謠言將無法在網絡中傳播。

社交網絡;博弈論;謠言擴散;行為決策

0 引 言

在線社交網絡源于20世紀60年代Milgram提出的六度分離理論[1]。社交網絡自誕生以來發展迅速，在線社交網絡巨頭Facebook財報顯示，2014年第一季度Facebook活躍用戶人數已達12.8億，其中移動活躍用戶人數超過10億[2]。日益增大的網絡規模與不斷進步的通訊技術，在方便用戶日常交流、分享信息的同時，也促進了謠言、不良廣告等惡意消息的傳播，對網絡安全、社會經濟等造成了一定的損害[3-4]。

學者們對于社交網絡的研究大多基于復雜網絡理論。在網絡研究模型方面，Watts等研究了網絡的聚類性質，提出了WS小世界網絡模型，為分析社交網絡的小世界特性提供了理論依據[5]；Barabási等通過研究發現萬維網的出度和入度分布與正態分布有很大不同，而是服從冪律分布，并提出了BA無標度模型[6]。此后，大多數學者基于上述兩種經典模型，根據不同網絡的拓撲特征進行改進與修正，對模型加以推廣[7-8]。在傳播動力學研究方面，由于謠言在網絡中的傳播機制與生物病毒網絡中的傳染病模型有許多相似之處，因此利用傳染病模型研究謠言傳播過程得到了許多學者的青睞，其最早可以追溯到1964年Daley等建立的D-K模型討論謠言傳播機制[9]。此后，Moreno等將該模型推廣至異構網絡并給出其場均方程[10]。由于社交網絡中的節點是現實生活中的用戶，其傳播行為具有很高的自主性和獨立性，其行為決策難以直接利用傳染病模型進行描述，因此需要對單個節點的行為決策及其鄰居節點之間的相互影響進行研究。Simon等通過研究發現，在疾病傳染、購物、社交等情況下，用戶的決策行為受到其鄰居或者朋友的影響，人們會根據他人的決策制定并修改自己的行為決策[11-13]。Jackson等分析了社交網絡中的博弈論，其中每個用戶都將做出一個二元選擇[14]。而Lopez則分析了鄰居節點對用戶決策的影響并給出了場均方程[15]。

基于網絡博弈模型，分析在利益驅動下用戶對于網絡謠言傳播的行為決策，并給出謠言擴散動力學的場均方程，通過數值仿真分別分析無標度網絡和小世界網絡中，不同模型參數對于謠言傳播的影響。發現用戶決策轉換比例中的固有影響因子與時間速率因子對謠言在網絡中的擴散具有顯著影響，隨著時間速率因子的增大，謠言在網絡中的擴散速率及擴散規模有所下降，同時當時間速率因子足夠大時，用戶的決策轉化比例減小。并且隨著固有影響因子的減小，謠言在網絡中的擴散速率下降，但與時間速率因子不同，固有影響因子的減小僅減慢了謠言在網絡中的擴散速度，對于謠言最終擴散規模并沒有產生顯著影響。

1 社交網絡中的網絡博弈模型

社交網絡中的謠言傳播過程與生物病毒網絡中的病毒擴散機制十分相似，因此利用病毒網絡中的傳染病模型來研究社交網絡中的謠言傳播機制受到了諸多學者的青睞。與此同時，信息傳播與病毒擴散仍有許多不同之處。首先，病毒網絡中易感人群通過接觸感染者，以一定概率被動地感染，成為感染者，而社交網絡中，用戶通過理性判斷，自主做出決策是否傳播謠言或者只讀謠言；病毒網絡中，一旦成為感染者，感染人群將在一段穩定的時間內保持感染狀態，而在社交網絡中，每時每刻用戶都可以選擇傳播謠言或者只讀謠言的狀態，具有很高的自主性和獨立性。

考慮到社交網絡中用戶做出決策是理性自主的，同時用戶的行為決策受到其鄰居節點的影響，許多學者利用博弈論的概念來刻畫這種影響，將謠言在網絡中的擴散過程，看作是用戶通過博弈選取最佳決策，使自身利益最大化的過程。這里將用戶與多個鄰居節點之間的博弈看作是多個雙人博弈的組合，且對于一個用戶節點而言，任意兩個鄰居節點之間的決策相互獨立。博弈論中最核心的概念是納什均衡，指自私個體在相互作用過程中達到的一種均衡狀態，在這種狀態下沒有個體可以通過單方面改變自己的策略而增加收益，因此，也可利用納什均衡來判斷社交網絡謠言傳播穩態時，各個用戶節點的決策分布。

考慮如下的收益矩陣(見圖1)，其中1表示傳播謠言，0表示只讀謠言。

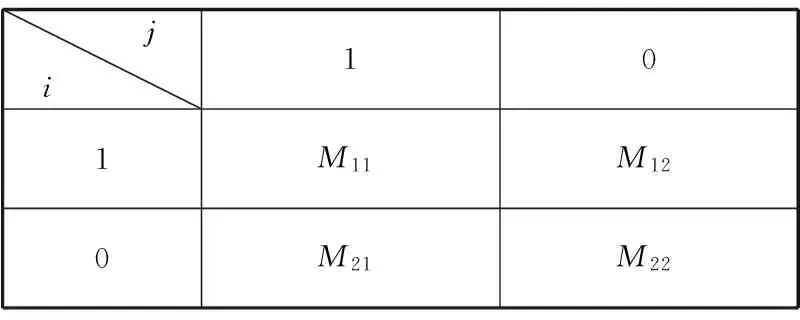
ji 101M11M120M21M22

圖1 網絡博弈收益矩陣

根據不同的矩陣元素值，可對博弈模型進行分類。對于合作博弈模型，將行為1視為選擇合作，0視為放棄合作，博弈雙方合作需要付出成本，同時合作成功(即博弈雙方都選擇行為1)帶來的收益也大于成本，即有M11>M21，M22>M12。此外，根據不同的收益矩陣元素值，較為經典的博弈模型還有囚徒困境博弈模型：M21>M11>M22>M12，以及雪堆博弈模型：M21>M11>M12>M22。

對于網絡中一個度為K的用戶，假定t時刻其鄰居節點中有nK(t)個節點選擇傳播謠言，則其選擇傳播謠言和選擇只讀謠言的收益分別為：

u(1|K,nK(t))=M11nK(t)+M12(K-nK(t))

(1)

u(0|K,nK(t))=M12nK(t)+M22(K-nK(t))

(2)

由于用戶決策均是理性自主的，因此用戶總是選擇使自己收益最大的決策，當用戶的鄰居節點選擇行為1人數比例nK(t)/K高于q時，最佳決策為采取行為1，反之亦然。其中，q稱為行為1的風險主導程度[16]：

(3)

由于網絡中，不同時刻用戶的行為決策可以改變，因此假定用戶做出決策時，其鄰居節點的決策是未知的。因此，用戶根據上一時刻鄰居節點做出的決策，通過博弈，做出可能獲取最大收益的決策。最后，認為謠言在社交網絡中的擴散過程是一個Markov進程[17]，即t時刻用戶做出的決策只與t-1時刻用戶的決策相關，與之前時刻的決策無關。

符號表示如下：

a:行為集，1表示接受并傳播謠言，0表示不傳播謠言，a={0,1}。

P(K):網絡中度為K的節點所占比例，即度分布。

nK(t):t時刻，度為K的節點選擇傳播謠言的鄰居個數。

x(t):t時刻，網絡中選擇傳播謠言的人數比例。

P(a|K,t):t時刻，有nK(t)個鄰居選擇傳播謠言，度為K的用戶選擇行為a的概率。

r(a|K,t):t時刻，度為K的節點，改變原策略選擇行為a的概率。

u(a|K,nK(t)):t時刻，nK(t)個鄰居選擇傳播謠言，度為K的節點選擇行為a獲取的收益。

pK(t):t時刻，度為a的節點中選擇傳播謠言的人數所占其比例。

2 網絡謠言擴散模型

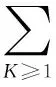
(4)

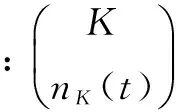
同時，假定t時刻，有nK(t)個鄰居選擇傳播謠言，度為K的用戶選擇行為a的概率為P(a|K,t)。由文獻[16]可知，由于網絡中的用戶是理性自主的，用戶行為決策的制定完全基于該行為帶來的收益，所以用戶選擇行為的概率服從0-1分布：

P(1|K,t)=

(5)

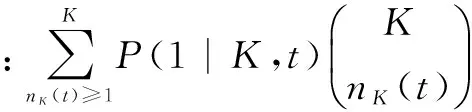
用戶在制定行為決策的同時，由于對謠言信息內容了解不夠全面，以及人類行為的隨機性，實際決策過程中可能做出與理論上的最佳決策相反的決策，這里可以定義α為用戶轉變決策的比例。對于網絡謠言擴散這一過程，隨著時間推移，用戶對謠言背景、真實性等內容的了解將不斷深入，做出的行為決策也將趨近于最大收益決策，因此，假定用戶轉變決策比例是關于時間t的負指數函數[18-19]：

α=μe-ρt

(6)

其中，μ為固有影響因子，即人類行為隨機性對決策的影響；ρ為時間速率影響因子，隨著時間推移以及人們的認識不斷深入，用戶決策轉換的比例將逐漸減小，當t→∞時，網絡達到穩態，決策轉換比例為0。

因此，對于度為K的節點，t時刻，轉變決策，采取行為1的概率為：

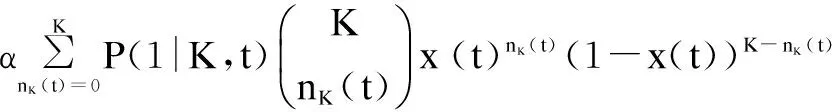
(7)

同理可得到轉變決策采取行為0的概率，且有α=r(0|K,t)+r(1|K,t)。由經典傳染病模型中的謠言傳播機制[20]，可得單位時間內，網絡傳播謠言人數比例變化率為：

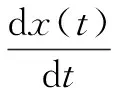
(8)

由式(8)可知，網絡傳播謠言用戶人數比例變化由兩部分組成，即t時刻，由行為0變為行為1的用戶人數，減去由行為1變為行為0的人數。

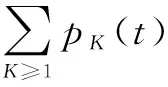
(9)

再將式(4)代入，即可得到穩態時不同節點度的用戶采取行為1的人數比例所應滿足的條件。

通過計算機仿真其理論值的具體算法步驟如下：

(1)生成初始無標度網絡，具體方法為：生成初始全連通網絡(50個節點)，每次向網絡中添加1個新節點以及10條連邊，連接概率與網絡已有節點的度成比例，重復添加節點與連邊，直至網絡節點數達到5 000。

(2)假定網絡初始謠言傳播人數比例為1%，即50個節點傳播謠言，隨機確定無標度網絡中的50個節點，并由此得到t=0的初始時刻不同節點度的pK(t0)。

(3)在t=0時刻，由式(4)確定網絡中傳播謠言人數比例x(t0)。

(4)在t=1時刻，由式(10)計算各個節點度節點的傳播謠言人數比例：

pK(t1)=pK(t0)-αpK(t0)+r(1|K,t)

(5)在t=1時刻，確定網絡中謠言傳播人數比例x(t1)。

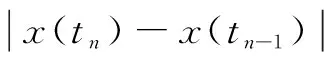
(7)重復步驟(3)～(5)，直至步驟(6)成立。

3 模擬仿真

考慮到現實中的在線社交網絡與規則網絡有很大不同，早在1998年，Watts和Strogatz發現了網絡的小世界特性[5]，小世界網絡模型的聚類特征十分契合在線社交網絡的六度分離理論。而在1999年，Barabási和Albert就提出了網絡的無標度特性[6]，網絡中大部分節點度數較小，存在小部分hub節點的度分布也十分符合實際社交網絡中的度分布情況。因此，分別構建無標度網絡模型與小世界網絡模型對網絡中的謠言擴散進行理論分析。

在無標度網絡中，由于存在少量hub節點，這些節點度數很大，是網絡的中心節點，在網絡信息傳播過程中具有重要作用。大多數節點度數較小，不規則地分布在hub節點周圍，無標度網絡不具有明顯的特征標度，其度分布近似滿足長尾分布。而小世界網絡中，部分區域的節點連接緊密，彼此之間的路徑長度較短，形成社團，具有較為明顯的聚類性質。

小世界網絡具有較短的平均距離，其構造基于對完全規則網絡以固定的概率p進行隨機重連，當p=0時，網絡即是規則網絡，當p=1時，網絡為隨機網絡，因此小世界網絡介于二者之間，這里選取重連概率p=0.1進行網絡構造。其中參數選取為：q=0.1，μ=1，ρ=0.05，初始謠言傳播人數比例為0.01。

如圖2所示，無標度網絡與小世界網絡中謠言傳播人數比例隨謠言擴散次數變化圖像呈現出S-型曲線，即在擴散初期，謠言擴散速率較慢，隨著擴散次數推移，謠言在網絡中迅速擴散，當擴散至一定程度時，謠言擴散速率逐漸下降，網絡狀態趨于平穩。同時，相較于無標度網絡，謠言在小世界網絡中的傳播較為緩慢，在謠言爆發之前具有較長的潛伏期，這是由于小世界網絡具有社團結構的特征，謠言往往先在社團內部擴散，再以一定概率通過社團內部成員與外部的連接，向外部傳播。因此，小世界網絡的社團結構對于謠言在網絡中的擴散具有抑制作用，李嬋嬋等在病毒網絡中也發現了相似的結論[21]。

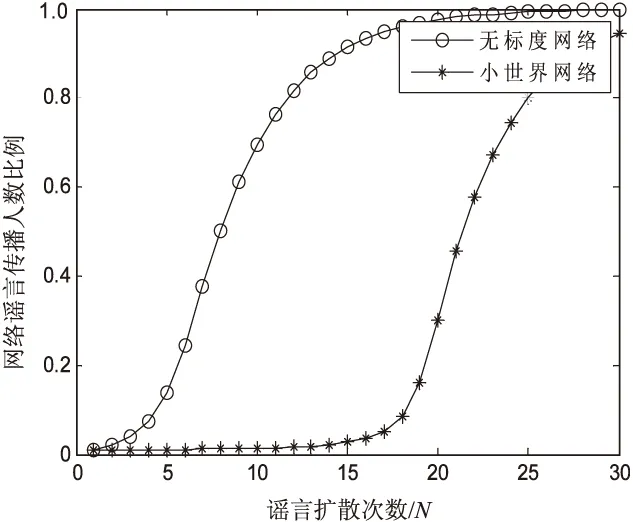
圖2 小世界網絡與無標度網絡謠言傳播 人數比例隨擴散次數變化曲線

為進一步分析謠言在無標度網絡與小世界網絡中的擴散過程以及用戶轉換決策比例對謠言傳播的影響，分別固定固有影響因子和時間速率影響因子，在不同參數下，做出無標度網絡與小世界網絡中謠言傳播人數比例隨擴散次數變化曲線，如圖3和圖4所示。

通過圖3(a)發現，在相同條件下，隨著時間速率因子的增大，謠言在網絡中的擴散速率及擴散規模有所下降；當ρ=0.15時，謠言在網絡中無法擴散。這是由于在謠言擴散初期，網絡中謠言傳播人數較少，大多數用戶的最佳決策為不傳播謠言，同時，當時間速率因子足夠大時，用戶的決策轉化比例減小，用戶幾乎不會更改自己的決策，因此用戶將堅持不傳播謠言的決策，從而導致謠言無法傳播。

圖3(b)則表明，在相同條件下，隨著固有影響因子的減小，謠言在網絡中擴散速率下降，但與時間速率因子不同，隨著固有影響因子的減小，謠言擴散規模并沒有明顯下降。這是由于時間速率因子在用戶決策轉話比例中，位于指數項，且隨著擴散次數的增大，時間速率因子的影響將被放大，對于較大的時間速率因子，如ρ=0.15，當擴散次數達到30時，決策轉化比例α≈0.01，而固有影響因子對于決策轉化比例的影響則是固定的，不會隨著擴散次數的增大而變化，因此固有影響因子的減小僅減慢了謠言在網絡中的擴散速度，對于謠言最終擴散規模并沒有顯著影響。

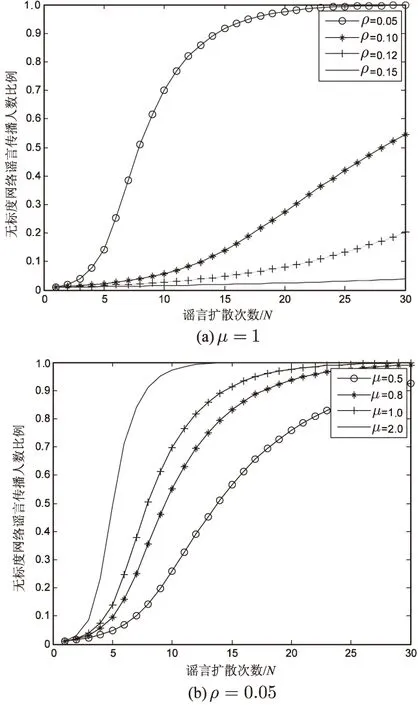
圖3 謠言傳播人數比例隨擴散次數變化曲線 (無標度網絡)

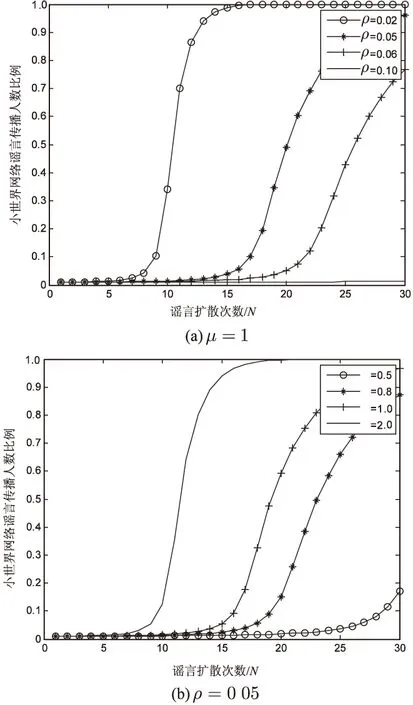
圖4 謠言傳播人數比例隨擴散次數變化曲線 (小世界網絡)

通過圖4發現，在相同條件下，分別改變時間速率因子與固有因子，其結論與無標度網絡中的相同；同時，相比圖3，小世界網絡中的謠言擴散速率與規模也相對較小，這是由于小世界網絡的社團結構對謠言傳播的抑制作用所產生的影響。

4 模型及仿真分析

由于通過式(6)求解穩態時網絡謠言傳播人數比例的理論值十分困難，一般考慮充分條件1，如文獻[16]認為網絡達到穩態時，對?K≥1，應滿足：

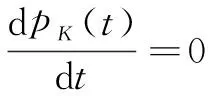
(10)

同時，有：

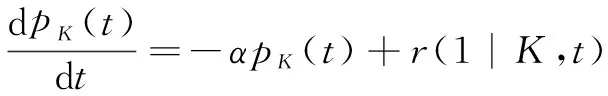
(11)

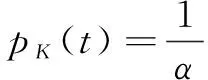
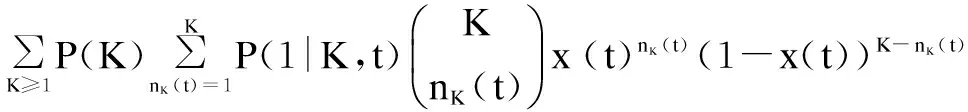
(12)

式(9)的解即為穩態時網絡中傳播謠言人數比例。同時，根據式(3)和式(5)可將式(9)改寫為：

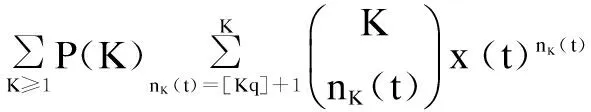
(13)

下面，將分析風險主導程度q對網絡謠言擴散的影響。圖5為無標度網絡中傳播謠言人數比例在不同風險主導程度下隨謠言擴散次數變化的曲線圖。

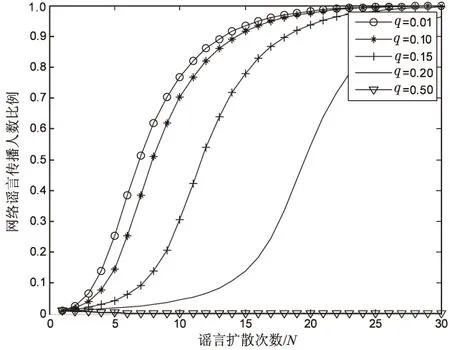
圖5 不同風險主導程度q下無標度網絡謠言 傳播人數比例隨擴散次數變化曲線

通過圖5發現，對模型進行簡化后，網絡中謠言傳播人數比例隨擴散次數變化圖像仍為S-型曲線，且隨著q的增大，謠言擴散速率和最終擴散規模不斷減小。當q較小時，謠言擴散速率和擴散規模變化很小，這是由于當q<1/([Kmax]+1)時，對任意的節點度K，[Kq]+1恒等于1，因此穩態時的傳謠謠言人數比例不會發生變化。同時從博弈論角度分析，當q較小時，無論鄰居節點傳播謠言人數比例大小，用戶的最佳決策為傳播謠言；相反地，當q較大時，用戶的最佳決策為不傳播謠言。因此，對于較大的q值，謠言在網絡中將無法傳播。

通過仿真發現，用戶決策轉換比例中的固有影響因子與時間速率因子對謠言在網絡中的擴散具有顯著影響，隨著決策轉換比例的減小，謠言擴散速率與最終擴散規模將出現不同程度的減小，且相較無標度網絡，小世界網絡的社團結構對謠言傳播具有抑制作用。同時，根據收益矩陣定義的風險主導程度對謠言擴散也會產生影響，但不同于決策轉換比例，當風險主導程度足夠小時，無論其如何變化，謠言必定擴散至整個網絡，相反，對于足夠大的風險主導程度，謠言將無法在網絡中傳播。

5 結束語

基于網絡博弈論研究社交網絡中用戶行為決策對謠言擴散過程的影響，實驗表明隨著決策轉換比例的減小，謠言擴散速率與最終擴散規模將出現不同程度的減小，且相較無標度網絡，小世界網絡的社團結構對謠言傳播具有抑制作用。同時，當風險主導程度足夠小時，無論其如何變化，謠言必定擴散至整個網絡，相反地，對于足夠大的風險主導程度，謠言將無法在網絡中傳播。

[1]TraversJ,MilgramS.Anexperimentalstudyofthesmallworldproblem[J].Sociometry,1969,32(4):425-443.

[2] 李 駿.Facebool：“全球第一大社交網站”快速成長的秘密[J].傳媒評論,2014(5):36-38.

[3]MeschGS.Parentalmediation,onlineactivities,andcyberbullying[J].Cyberpsychology&BehaviortheImpactoftheInternetMultimedia&VirtualRealityonBehavior&Society,2009,12(4):387-393.

[4]NicholasDF.Rumourresearchcandousedigitalwildfires[J].Nature,2013,493(7431):135.

[5]WattsDJ,StrogatzSH.Collectivedynamicsof‘small-world’networks[J].Nature,1998,393(6684):440-442.

[6]BarabásiAL,AlbertR.Emergenceofscalinginrandomnetworks[J].Science,1999,286(5439):509-512.

[7]WangJ,ZhaoL,HuangR.2SI2Rrumorspreadingmodelinhomogeneousnetworks[J].PhysicaAStatisticalMechanics&ItsApplications,2014,413:153-161.

[8]ZanY,WuJ,LiP,etal.SICRrumorspreadingmodelincomplexnetworks:counterattackandself-resistance[J].PhysicaAStatisticalMechanics&ItsApplications,2014,405:159-170.

[9]DaleyDJ,KendallDG.Epidemicsandrumours[J].Nature,1964,204(4963):1118.

[10]NekoveeM,MorenoY,BianconiG,etal.Theoryofrumourspreadingincomplexsocialnetworks[J].PhysicaAStatisticalMechanics&ItsApplications,2007,374(1):457-470.

[11]SimonS,AptKR.Choosingproductsinsocialnetworks[C]//Proceedingsof8thWINE.Liverpool,U.K.:[s.n.],2012:100-113.

[12]Sunds?yPR,BjellandJ,CanrightG,etal.Comparingandvisualizingthesocialspreadingofproductsonalargesocialnetwork[M]//Influenceoftechnologyonsocialnetworkanalysisandmining.Vienna,Austria:Springer,2013:201-225.

[13]SenS,JinY,GuerinRA,etal.Modelingthedynamicsofnetworktechnologyadoptionandtheroleofconverters[J].IEEE/ACMTransactionsonNetworking,2010,18(6):1793-1805.

[14]JacksonMO,YarivL.Diffusionofbehaviorandequilibriumpropertiesinnetworksgames[J].AmericanEconomicReview,2007,97(2):92-98.

[15]López-PintadoD.Thespreadoffree-ridingbehaviorinasocialnetwork[J].EasternEconomicJournal,2007,34(4):464-479.

[16]López-PintadoD.Contagionandcoordinationinrandomnetworks[J].InternationalJournalofGamesTheory,2006,34(3):371-381.

[17]vanMieghemP.Performanceanalysisofcomplexnetworksandsystems[J].JournalofStatisticalPhysics,2007,126(3):725-727.

[18]LermanK,HoggT.Usingamodelofsocialdynamicstopredictpopularityofnews[C]//Proceedingsofthe19thinternationalconferenceonworldwideweb.[s.l.]:ACM,2010:621-630.

[19] 劉天華,張志華,李大偉,等.Weibull分布更新函數的指數近似算法[J].北京航空航天大學學報,2012,38(6):816-818.

[20]MorenoY,PastorsatorrasR,VespignaniA.Epidemicoutbreaksincomplexheterogeneousnetworks[J].PhysicsofCondensedMatter,2001,26(4):521-529.

[21] 李嬋嬋,蔣國平,宋玉蓉.動態小世界社團網絡上的病毒傳播研究[J].復雜系統與復雜性科學,2014,11(3):33-39.

Investigation on Rumor Diffusion Modeling with Network Game Theory

YU Sha-sha1，WANG You-guo1,ZHU Liang2

(1.College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210046,China;2.College of Telecommunications & Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

With the continual development of network technology,the online social network has become an important platform for people to express views and interact with each other.In view of this,a rumor diffusion model has been formulated and the rumor dissemination mechanism has been studied to give guidance and help to control the spread of rumors.Human behave in online social network,having an inclination to spread information so as to gain reputation or money etc.Therefore,a probability of an individual’s choice of spreading rumors or not has been proposed on the basis of game theory.The processes of rumor diffusion and the behavior characteristics have been taken into consideration to establish a rumor diffusion model in online social networks.Simulations on both scale-free network and small-world network have been conducted to investigate the impact of rate at which an individual revises his action on rumor diffusion.Its results indicate that small rate at which an individual revises his action on rumor diffusion can cut down the diffusion of gossip in varying degrees and that when the degree of risk dominance is small enough,the rumors would be spread to the entire network,no matter how it changes.

online social network;game theory;rumors diffusion;behavioral decision making

2016-06-14

2016-09-28

時間：2017-03-07

國家自然科學基金資助項目(61179027)；江蘇省“青藍工程”基金(QL06212006)；江蘇省高校研究生科研創新計劃項目(KYLX15_0831)

余莎莎(1990-)，女，碩士研究生，研究方向為信號處理理論與應用；王友國，博士生導師，教授，研究方向為信息理論及應用、編碼理論與應用、隨機共振理論與研究。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170307.0922.076.html

TP39

A

1673-629X(2017)04-0006-06

10.3969/j.issn.1673-629X.2017.04.002