定流值比例的最小雙費用流算法研究
趙禮峰,劉艷清
(南京郵電大學 理學院,江蘇 南京 210003)
定流值比例的最小雙費用流算法研究
趙禮峰,劉艷清
(南京郵電大學 理學院,江蘇 南京 210003)
現有最小雙費用流算法只能求解網絡的最大雙流問題,并不能得到定流值比例。為此,提出了一種定流值比例的最小雙費用流新算法,在求解最小雙流和最小費用的基礎上,在調整雙流值保證定流值比例的同時得到最小費用流。所提出的新算法定義了余網絡和費用差,以鄰接矩陣為網絡數據存儲結構,使用Ford算法分別得到兩費用的最短增廣鏈,選擇費用最小的增廣鏈增廣并求出其對應的費用差,從費用差最小的開始調整流值就得到定流值比例下的最小費用。應用該新算法構建定流值比例的最小雙費用流算法的運輸網絡模型,就可以獲得最優運輸方案。邏輯推理和仿真實驗結果均表明,所提出的算法可行、有效,能較好地解決稀疏網絡以及復雜網絡中定流值比例的最小雙費用流問題。
最小雙費用流算法;余網絡;鄰接矩陣;Ford算法;費用差
0 引 言
最小雙費用流問題是網絡優化中的一個核心問題,許多網絡優化問題都可歸結為最小雙費用流問題的特例,如最短路[1-2]、最大流[3-5]以及最小費用最大流[6-8]問題,這些網絡優化問題都可歸為單可行流算法研究。隨著物流運輸的發展,這些單可行流算法研究已經滿足不了運輸行業不斷發展的需要。由此,謝政和湯澤瀅根據一個實例建立了在容量—費用雙流網絡中求最小費用最大雙流的模型[9],提出了最小費用最大雙流和雙流增量網絡的充要條件,該算法證明了最小費用最大雙流算法的正確性。謝政和肖予欽提出了在(vs,vt)平面雙流網絡中的最小費用最大雙流[10],利用(vs,vt)平面雙流網絡的平面性,找出并證明了該網絡中最小費用雙流的充要條件,該算法更易于在計算機上實現。馬宇斌、謝政等提出了一種求解最小雙費用流問題的算法[11],通過實際應用案例,抽象出一種帶容量限制的雙費用權網絡模型,并由此提出了相應的最小雙費用流問題。借鑒網絡分層的思想,根據雙費用權網絡的特點,設計出一個求解該問題的雙層原始對偶算法。文獻[9-11]都是關于雙可行流的算法研究,這些算法很好地解決了單可行流算法解決不了的問題。但是對運輸的兩種產品有定運輸比例要求時,以上三種雙費用流算法明顯就不再適用,由此在文獻[9-11]的理論基礎上,提出了一種定流值比例的最小雙費用流算法。
在文獻[9-11]中得到了網絡中的最大雙流,由于每次都選擇費用最小的增廣鏈增廣流值,這就造成了得到的比值往往不是兩流值的定流值比例。可以通過調整雙流的流值得到定流值比例,而每調整一個單位可行流,總費用就會增加,為此產生了如何調整雙流的比值才能使其總費用最小,每調整一個流值總費用會增加多少的問題。新算法是在求得的最大雙流和最小費用的基礎上,每得到一個增廣鏈增廣流值時,求出其對應的費用差。每調整一個流值,總費用就增加對應的費用差的值,所以從費用差最小的開始調整流值就能實現既得到要求的流值比例又使得費用最少。通過模型建立與求解以及仿真實驗表明,新算法具有完全的可行性和有效性。
1 基本概念


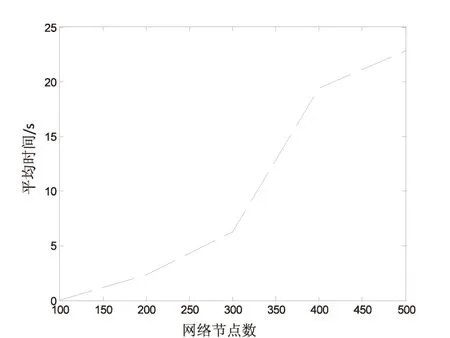
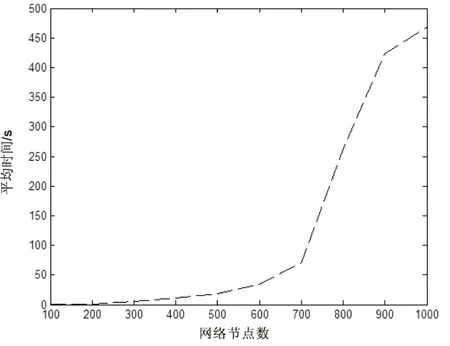
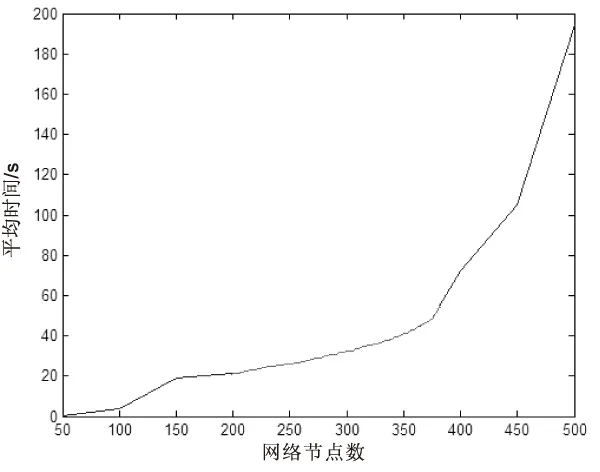
定義3(余網絡)[9]:設f是N上一個單可行流,按如下規則修改網絡N:對于N中任意一條弧aij=(vi,vj)∈A,若fij=cij,則刪掉弧aij;若0 2.1 算法思想 2.2 算法步驟 Step1:令f1=0,f2=0。 Step2:構造余網絡D(f1,f2),若D(f1,f2)中不存在關于費用w1和w2的(vs,vt)路,轉Step4,否則,在D(f1,f2)中用Ford算法找一條關于w1的最小費用路s1和關于w2的最小費用路s2,σi是si的容量(i=1,2)。 Step3:當w1(s1)≤w2(s2)時,沿路s1對f1增廣流值σ1,得到新可行流仍記為f1,轉Step1;當w1(s1)≥w2(s2)時,沿路s2對f2增廣流值σ2,得到新可行流仍記為f2,轉Step2。 2.3 算法的可行性分析 該算法執行時,每找到一條增廣鏈增廣流值,會重新構造余網絡,在余網絡中繼續尋找增廣鏈直至找不到增廣鏈為止。由于先前對于余網絡的定義是對于N中任意一條弧aij=(vi,vj)∈A,若fij=cij,則刪掉弧aij;若0 2.4 算法的時間復雜度 設N的頂點數為n,有向弧數為m,v*為最大雙流的流值,并且假設N中所有弧容量以及v*均為整數,在算法執行過程中,每次增廣的流值最多為1,因此最多經過v*次增廣,所以Step2到Step3的循環次數不超過v*。Ford算法的復雜性為O(nm),在Step2中需要分別求出兩費用的最短路,所以Step2的復雜性為O(2nm),Step3沿最小費用路對流進行增廣的計算量為O(n)。Step4調整流值最大為v*,最多調整v*次。由此可知,定流值比例的最小雙費用流算法的復雜性為O(2nmv*)。 3.1 建立網絡模型 某企業想要將兩種不同的產品從產地運往倉庫,運輸過程是通過一個單行的公路網,公路網中有若干條運輸路線可供選擇,每條道路只能負擔有限重量的產品,不同的道路上單位產品的運費也不同,在同一條道路上,不同產品的運費也不同。那么給出一個模型使得該企業從產地運往兩種不同產品到倉庫且兩種產品的運輸比例為θ的方案,使得運輸量最多而總費用最小。不妨假設圖1為這個運輸網絡的一部分,運輸網絡有10個節點,為圖中圈起來的數字,每一條弧上第一個數字為每條運輸道路的最大負擔重量,第二個數字為第一種產品在每條運輸道路的運費,第三個數字為第二種產品在每條運輸道路的運費。 若將此運輸系統看作是一個從始點(產地)為節點1,終點(倉庫)為節點10的容量網絡N=(V,A,c,w1,w2,θ),其中,V表示節點1和節點10之間的兩條或者兩條以上道路的交匯點,A表示弧的集合,c表示每條運輸道路的最大負擔重量,w1和w2分別表示第一種產品和第二種產品在每條道路運費的集合,θ表示兩種產品的運輸比值。 圖1 運輸網絡 于是上述問題歸結為:求容量網絡N=(V,A,c,w1,w2,θ)的定流值比例的最小雙費用流算法。 3.2 求解網絡模型 用編制的MATLAB程序求出圖1兩流值比例為1∶2的最小雙費用流,如表1所示。其中,序號1~5表示有五條路徑,增廣路徑中列出從節點1到節點10的所有增廣路徑,f1為費用1在每條增廣路徑的增廣流值,f2為費用2在每條增廣路徑的增廣流值,w1(s1)和w2(s2)分別表示每一條增廣路徑關于費用1和費用2的費用,費用差ω是w1(s1)和w2(s2)的差的絕對值,w是圖1中的最小費用。從表中可以看到,兩流值的比例為1∶2,最小費用為275。 表1 網絡1中流值比為1∶2的最小雙費用流 表2 網絡1中流值比為1∶1的最小雙費用流 當需要的兩流值比例為1∶1,也就是說最大雙流為(7.5,7.5)時,需要從f2調整2.5個單位可行流到f1,序號3、4以及5是f2的增廣路徑,每從f2調整一個單位可行流到f1,總費用就會增加一個單位費用差的值,所以從費用差最小的4開始調整,調整2.5個單位的可行流如表2所示。最小費用w在275的基礎上增加10為285。用編制的MATLAB程序檢驗得到的結果和表2相同。 3.3 新算法在稀疏網絡中的運行時間 The initial resistance is defined as , and was found to be R0 ~ 8.5 kΩ in our case.ρM can be calculated as a function of either time or the statevariable x. 生成規模為n*n的隨機稀疏網絡,每條弧的流值、費用1以及費用2都是隨機生成的整數。為了減少計算機穩定性造成的誤差,以下所有實驗都進行10次仿真并取平均值。 當網絡的節點規模為500,流值比值設置為1∶2時的運行時間如圖2所示。 圖2 流值比例為1∶2的稀疏網絡平均運行時間(1) 從圖中可以得到,平均運行時間隨著節點數的增大而增大。對于節點規模為1 000,流值比值設置為1∶2的網絡來說,由于新算法的時間復雜性為O(2nmv*),隨著節點數、弧的個數以及總流值的增大運行時間呈次方增長,所以從圖3可以看到,節點數從500增加到1 000時運行時間直線上升。大量的仿真實驗結果表明,算法對于網絡規模為500個節點的運行時間比較穩定,當網絡規模超過500個節點時運行時間呈次方增長,運行時間稍長。 圖3 流值比例為1∶2的稀疏網絡平均運行時間(2) 3.4 新算法在復雜網絡中的運行時間 生成規模為n*n的隨機網絡,用round(10*rand(n))生成的隨機矩陣來構成隨機網絡,發現round(10*rand(n))生成的矩陣中每個節點平均與n-2個節點相連,每條弧的流值、費用1以及費用2都是隨機生成的整數,為了減少計算機穩定性造成的誤差,以下所有實驗都進行10次仿真并取平均值。 當網絡的節點規模為500,流值比值設置為1∶2時的運行時間如圖4所示。當節點規模為350時,運行時間開始直線上升,這是由于算法的時間復雜度為O(2nmv*),網絡中每個節點至少與n-2個節點相連,那么弧的個數m=(n-2)!,所以隨著節點數的增加,運行時間快速增加。 圖4 流值比例為1∶2的復雜網絡平均運行時間 通過圖2到圖4,比較和分析新算法在稀疏網絡以及復雜網絡運行時間的長短,表明新算法更適合執行較大規模的稀疏網絡,對于較小規模的較復雜網絡也很適用。 運輸問題一直是網絡最優化的重要研究方向,在運輸如此發達的今天,急需提高運輸物品的量同時降低運輸成本。為此,提出了一種定流值比例的最小雙費用流新算法,在構建余網絡下求得網絡中的最小雙費用流,在求解最小雙流和最小費用的基礎上,通過調整雙流值保證定流值比例的同時得到最小費用流算法。用MATLAB編制的程序能直接求出定流值比例,對于兩種商品運輸問題有很大的研究意義。大量的仿真實驗表明,算法對于稀疏網絡規模為500個節點的運行時間比較穩定,當網絡規模超過500個節點時運行時間呈次方增長,運行時間稍長;對于復雜網絡,當節點規模為350時運行時間上升稍快。目前隨著網絡規模的不斷增大,網絡規模趨于復雜化,而新算法經過邏輯推理以及仿真實驗,證明了其能求出稀疏網絡以及復雜網絡的固定流值比以及最小費用,具有較高的應用價值。 [1]CaiX,KloksT,WongCK.Time-varyingshortestpathwithconstraints[J].Networks,1997,29(2):141-149. [2]LoachimI.Adualprogrammingalgorithmfortheshortestpathproblem[J].Networks,1998,31(2):192-204. [3]DinicEA.Algorithmsforsolutionofaproblemofmaximum flowinnetworkswithpowerestimation[J].SovietMathematicalDoklady,1970,11(8):1277-1280. [4] 謝金星,邢文訓,王振波.網絡優化[M].北京:清華大學出版社,2009:177-181. [5]FordLR,FuldersonDR.AsimplealgorithmforfindingmaximalnetworkflowsandanapplicationtoHitchcockproblem[J].CanadianJournalofMathematics,1957,9:210-218. [6]HamacherHW,PedersenCR,RuzikaS.Multipleobjectiveminimumcostflowproblems[J].EuropeanJournalofOperationalResearch,2007,176(3):1404-1422. [7]ZhuXiaoyuan,YuanQi.Minimal-costnetworkflowproblemswithvariablelowerboundsonarcflows[J].Computers&OperationsResearch,2011,38(8):1210-1218. [8] 趙禮峰,宋常城,白 睿.基于最小費用最大流問題的“排序”算法[J].計算機技術與發展,2011,21(12):82-85. [9] 謝 政,湯澤瀅.最小費用最大雙流[J].高校應用數學學報,1996,11(1):97-104. [10] 謝 政,肖予欽.(vs,vt)平面雙流網絡中的最小費用最大雙流[J].數學理論與應用,1999,19(3):112-116. [11] 馬宇斌,謝 政,陳 摯.一種求解最小雙費用流問題的算法[J].計算機工程與科學,2014,36(3):446-451. [12] 厙向陽.點和邊有容量約束的網絡最小費用最大流算法[J].計算機應用研究,2010,27(8):3112-3114. [13] 謝 政.網絡算法與復雜性理論[M].北京:國防科技大學出版社,2003. Investigation on Minimum Double Cost Flow Algorithm with Constant Value Ratio ZHAO Li-feng,LIU Yan-qing (College of Mathematics and Physics,Nanjing University of Posts and Telecommunication,Nanjing 210003,China) The minimum double cost flow algorithm can only get the maximum double flow of the network,but it cannot get the required flow value ratio.So,a new algorithm of the minimum double cost flow with constant value ratio is put forward.It adjusts the double value to get the constant value ratio and make the cost least based on the maximal double value and minimal cost has gotten.The algorithm defines the over network and cost difference in it,with adjacency matrix as the network data storage structure,and it uses Ford algorithm to obtain shortest augmenting chain for two expenses and chooses the minimum cost augmented links to get the cost difference of augmented chain.It adjusts the double flow ratio based on the size of the cost difference.The algorithm is used to build the transportation network model of minimum double cost flow of constant flow ratio to get the optimal transportation scheme about the model.The logical reasoning and simulation results show that the algorithm proposed is completely feasible and effective,and it can effectively solve the problem of minimum double cost flow in sparse network and complex network. minimum double cost flow algorithm;over network;adjacency matrix;Ford algorithm;cost difference 2016-04-24 2016-08-17 時間:2017-03-07 國家自然科學基金資助項目(61304169) 趙禮峰(1959-),男,教授,碩士研究生導師,研究方向為圖論及其應用、矩陣論等;劉艷清(1989-),女,碩士研究生,研究方向為最短路、最大流以及最小雙費用流等。 http://kns.cnki.net/kcms/detail/61.1450.TP.20170307.0920.006.html TP301.6 A 1673-629X(2017)04-0094-04 10.3969/j.issn.1673-629X.2017.04.021

2 定流值比例的最小雙費用流算法
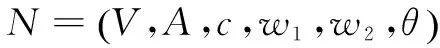
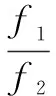
3 算法驗證



4 結束語

