非負矩陣譜半徑的新估計
鐘琴
(四川大學錦江學院數學教學部,四川 彭山 620860)
非負矩陣譜半徑的新估計
鐘琴
(四川大學錦江學院數學教學部,四川 彭山 620860)
非負矩陣譜半徑的估計是非負矩陣理論研究中的重要課題.如果譜半徑的上下界能夠表示為非負矩陣元素的易于計算的函數,那么這種估計價值更高.通過構造兩個收斂的序列得到非負矩陣譜半徑的新界值.數值算例表明其結果比有關結論更加精確.
非負矩陣;譜半徑;上界;下界
1 引言與預備知識
非負矩陣是矩陣理論中一個重要的矩陣類,在圖論、線性規劃、計算機科學、自動控制等領域中有廣泛的應用,尤其是對于Markov鏈理論、偏微分方程數值解的一般理論也有重要應用.對非負矩陣的譜半徑進行估計是非負矩陣理論研究的核心問題之一.許多學者都致力于這方面的研究,并取得了一系列的研究成果[111].
若A=(aij)n×n的所有元素aij≥0,則稱矩陣A為非負矩陣,記為A≥0;若aij>0,則稱矩陣A為正矩陣,記為A>0,用ρ(A)表示n階非負矩陣A的譜半徑.
設n階矩陣A=(aij)n×n,如果存在一個置換矩陣P使得PAPT=其中B和D分別是k,l階方陣,k≥1和l≥1,則稱A是可約矩陣,否則稱A是不可約矩陣.
若A是非負不可約矩陣,則存在正向量u,使得Au=ρ(A)u,其中u稱為A的右Perron特征向量.
非負矩陣譜半徑的最有名且用的最多的界值是由Frobenius[1]提出的.設
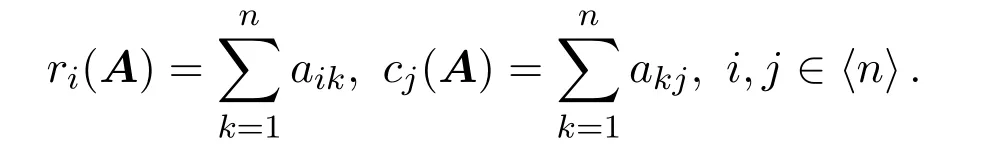
結論 1.1[1](Frobenius界值) 設A=(aij)n×n≥0,令
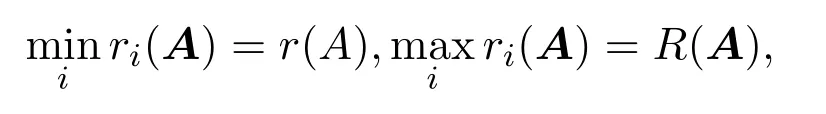
則

對于列和也有相同的結論.
正矩陣是非負矩陣的子類,具有非負矩陣的所有性質.W.Lederman[2],A.Ostrowski[3]和A.Brauer[4]在(1)式的基礎上給出了正矩陣譜半徑的界值定理.
對于具有非零行和的非負矩陣,H.Minc[5]對(1)式進行了改進,得到了如下的結果:
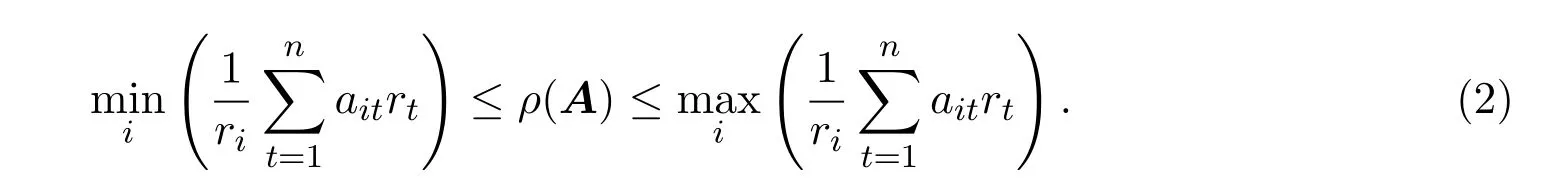
結論 1.2[6]設矩陣A=(aij)n×n≥0且不可約,若存在正整數k使得
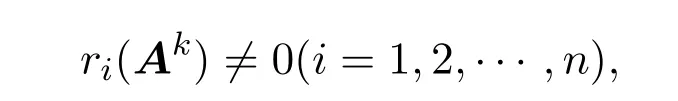
則
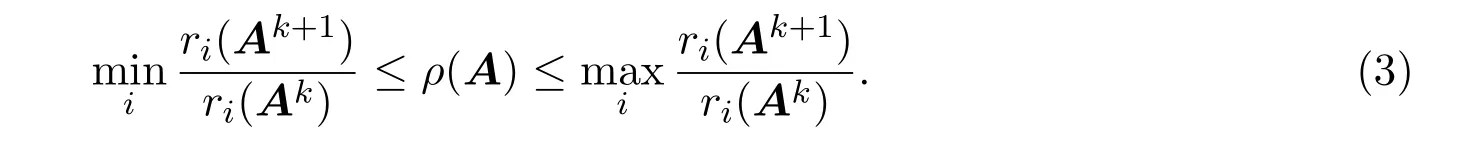
對于列和結論同樣成立.
結論 1.3[7]設矩陣A=(aij)n×n≥0且A具有非零行和非零列和,則對任意的正整數m,k有
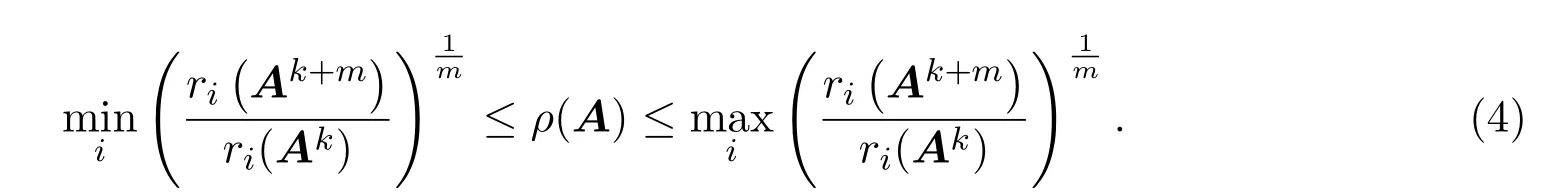
對于列和結論同樣成立.
本文在文獻[6-9]的基礎上對非負矩陣譜半徑的上下界進行改進,借助于一個特殊的矩陣,通過構造兩個收斂的序列,將非負矩陣譜半徑的上下界表示為矩陣元素的易于計算的函數,所得結果改進了現有的相關結論.
2 主要結論
引理 2.1[5]設λ是矩陣A的特征值,
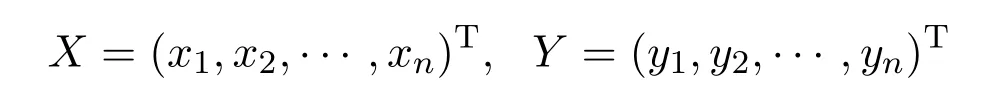
分別是矩陣AT和A對應于λ的特征向量,則
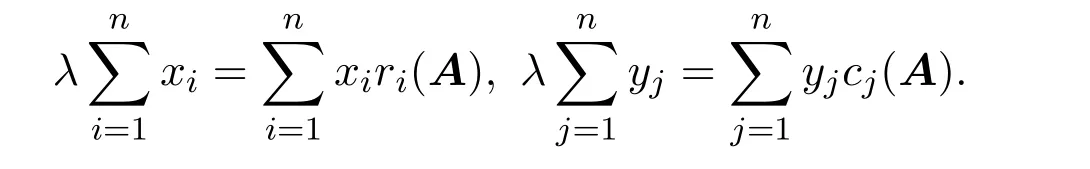
引理 2.2[5]若q1,q2,···,qn是正實數,則對任意實數p1,p2,···,pn,有
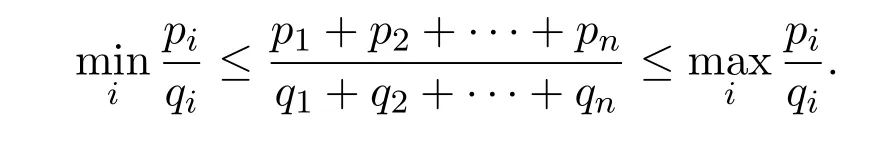
引理 2.3[7]設A是n階矩陣,ri(Ak),cj(Ak)分別表示矩陣Ak的第i行行和與第j列列和,則
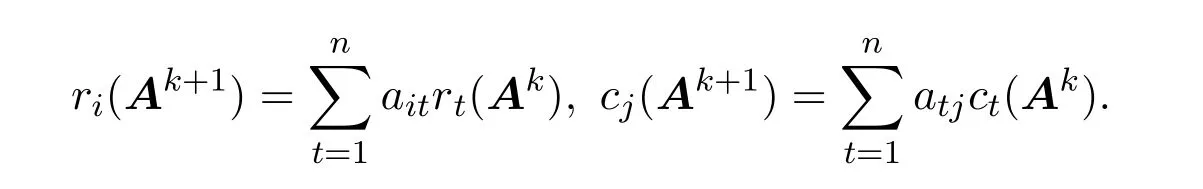
下面給出本文關于非負矩陣譜半徑的估計結果.
定理 2.1設矩陣A=(aij)n×n≥0且不可約,令
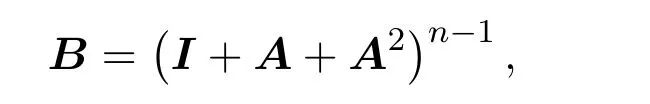
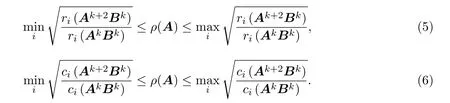
證明因為所以由引理3知設
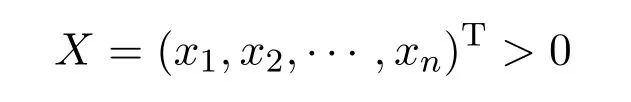
是矩陣AT對應于ρ(A)的特征向量,即
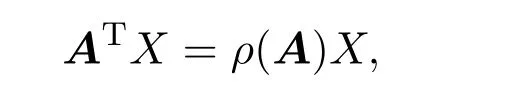
則有
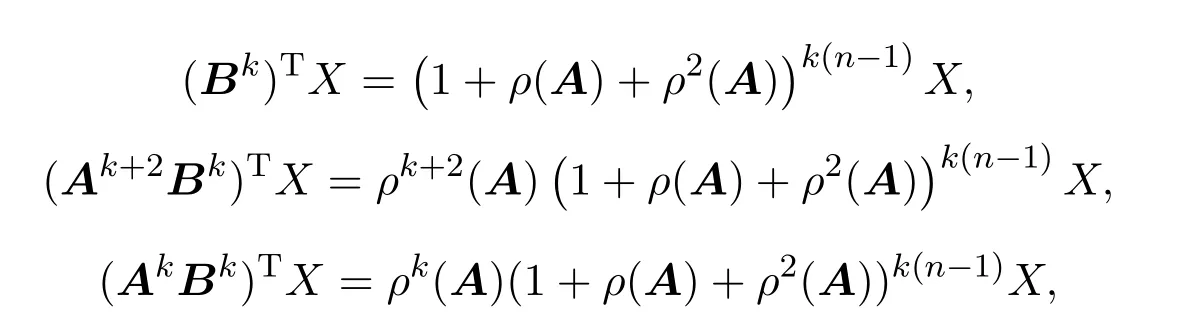
由引理1可知
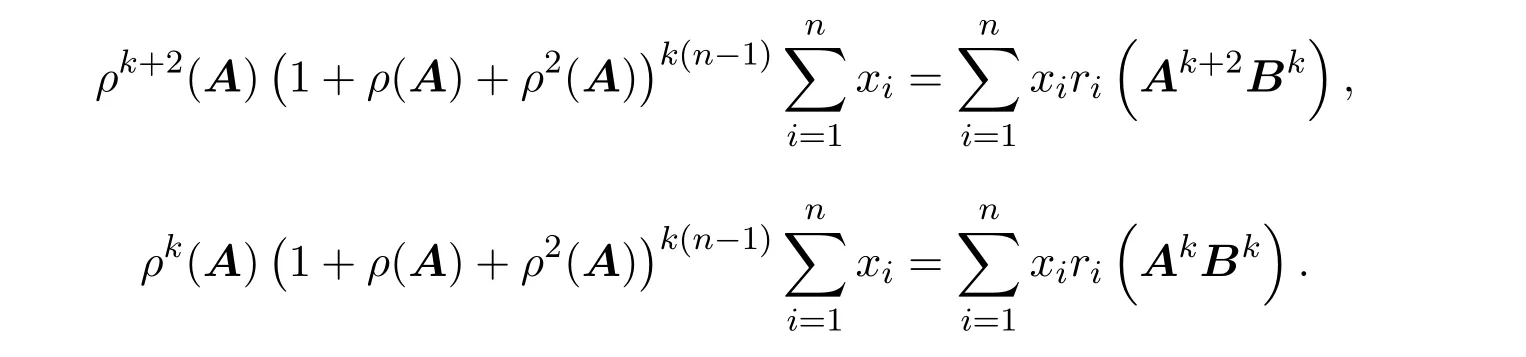
于是
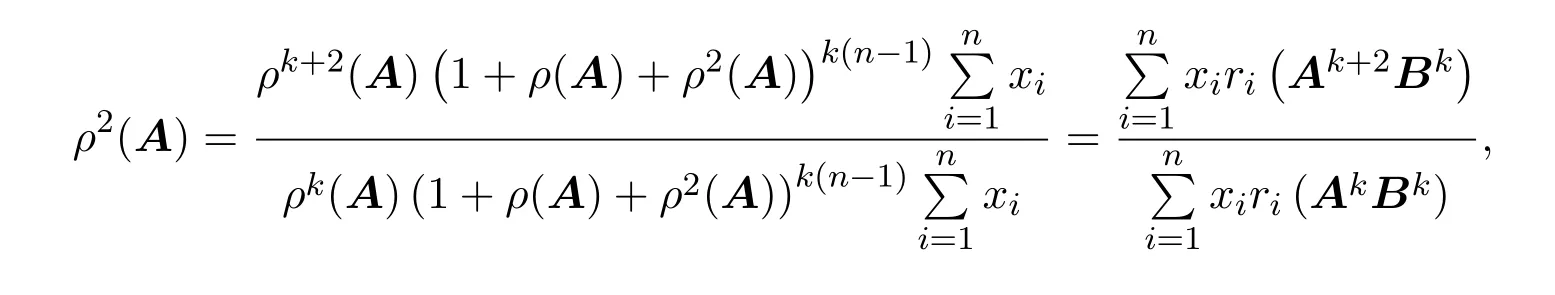
再由引理2得
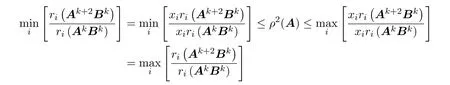
故(5)式得證,同理可證(6)式成立.
定理 2.2設矩陣A=(aij)n×n≥0且不可約,令
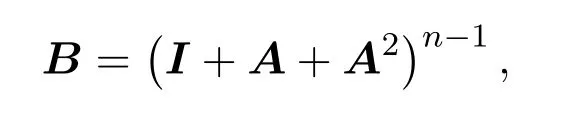
若
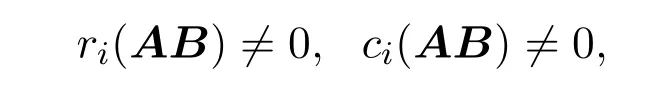
則對任意的正整數k,有
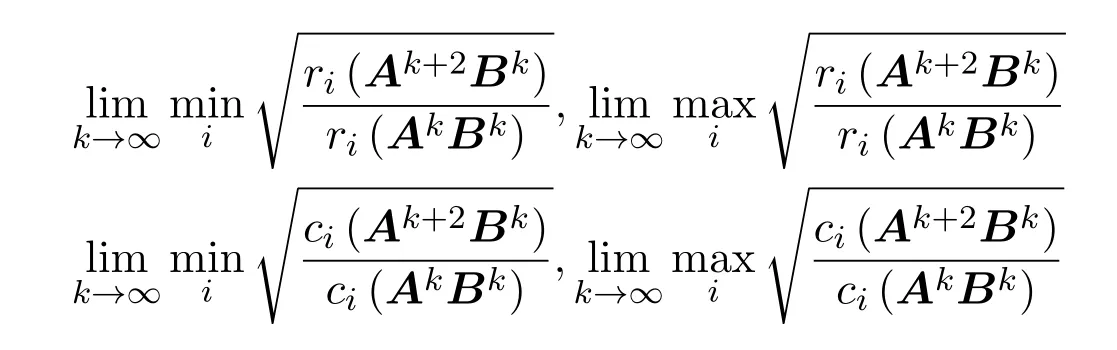
都存在,且有
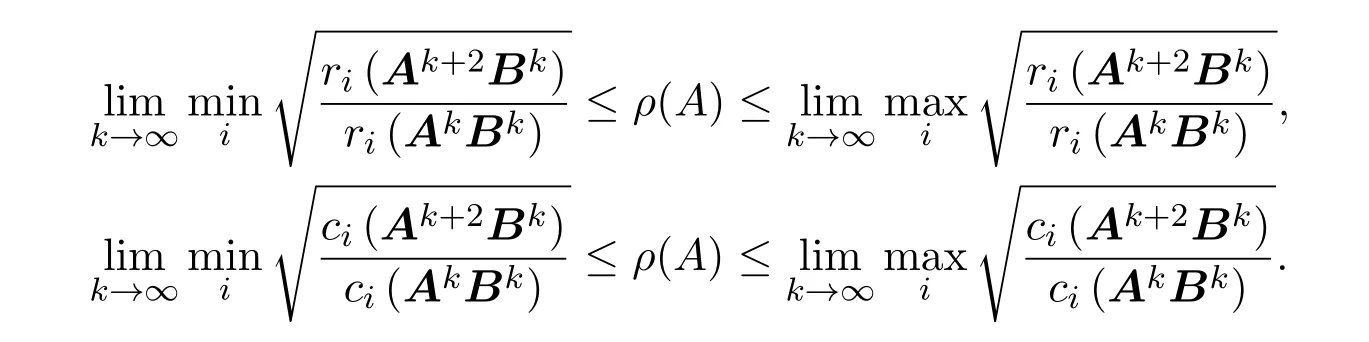
證明因為B=(I+A+A2)n?1,所以AB=BA,進一步有
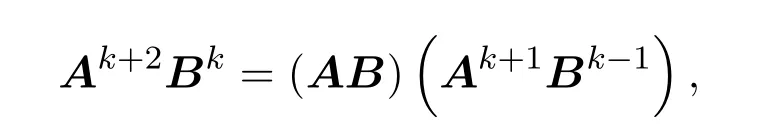
令AB=(cij),由引理2.3及引理2.2可知,對任意的正整數k,有
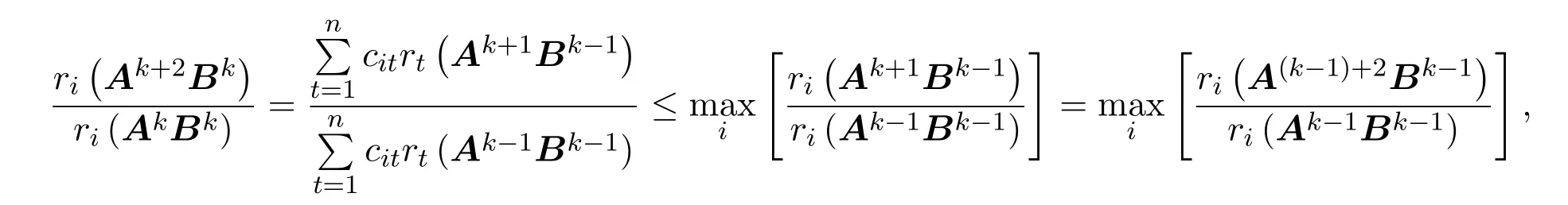
即
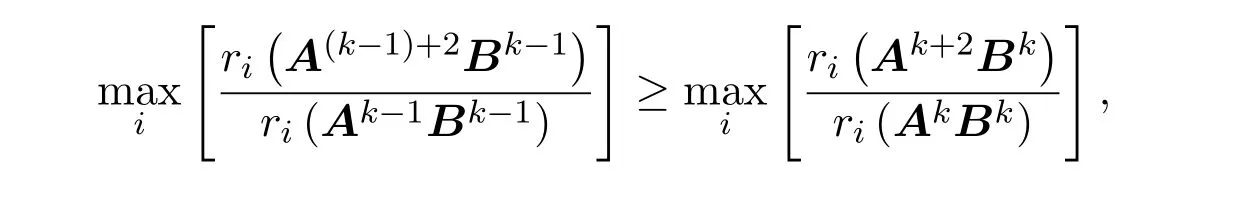
因此
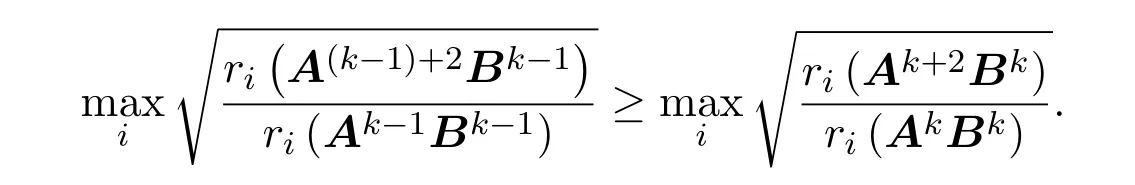
所以序列
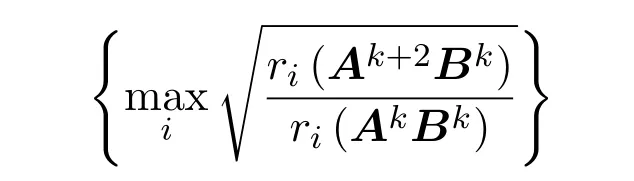
單調遞減且有下界ρ(A),從而極限存在.
根據定理2.1知:
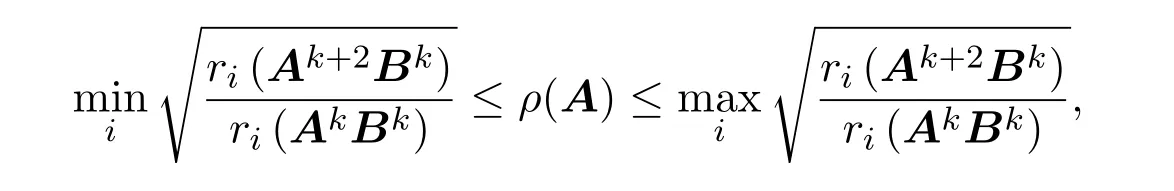
兩邊同時取極限得
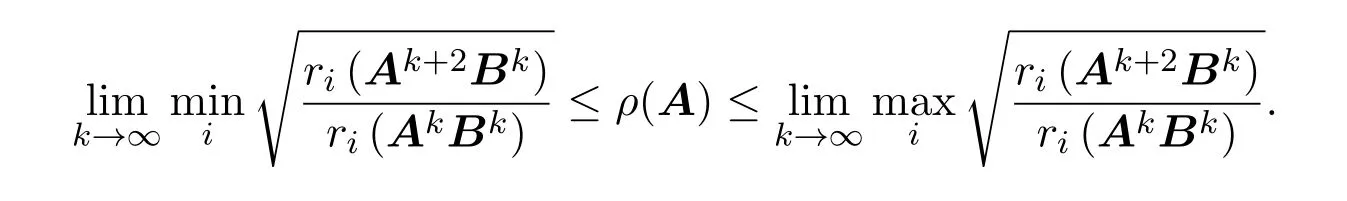
同理可證對列和的結論也成立.
注2.1在(5)式中令k=0,并規定A0=B0=I,則有
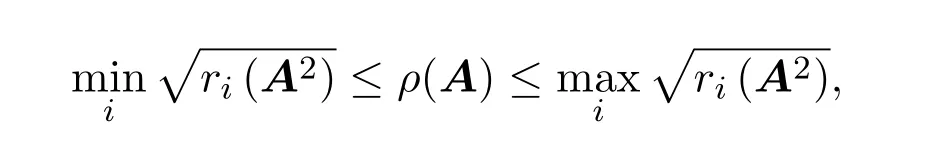
因為
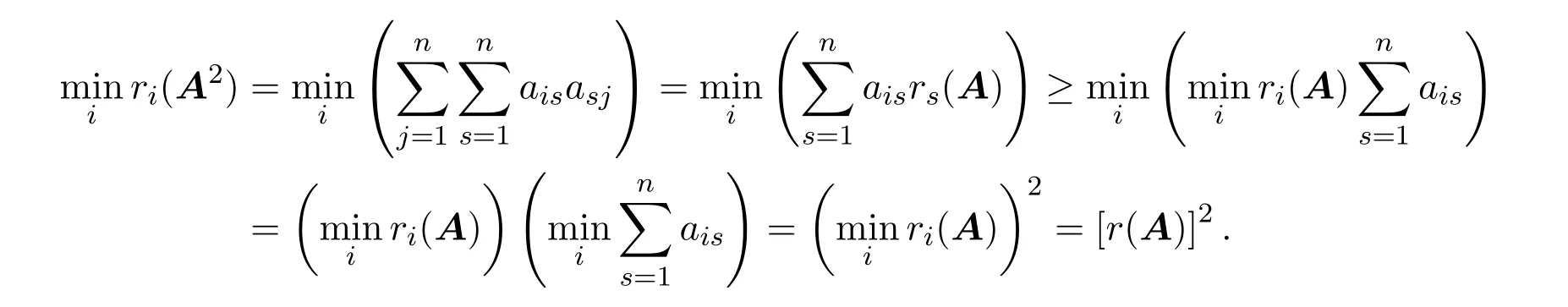
同理有
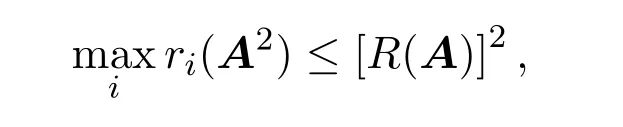
又根據ρ(A2)=[ρ(A)]2,從而有
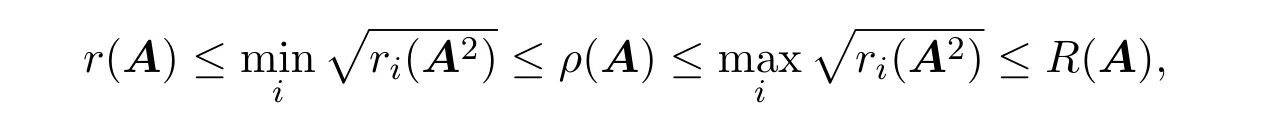
因此,定理2.1的界值是文獻[1]中(1)式的改進,且精確度更高.
注2.2定理2.1中ρ(A)的上下界表達式里容易計算,因為從引理2.3可知Ak+2Bk和AkBk的行和可以由Ak+1Bk?1和Ak?1Bk?1的行和遞推地算出,計算量不大.
注2.3若A是n(n≥2)階非負可約矩陣,則存在n階置換矩陣P,使得
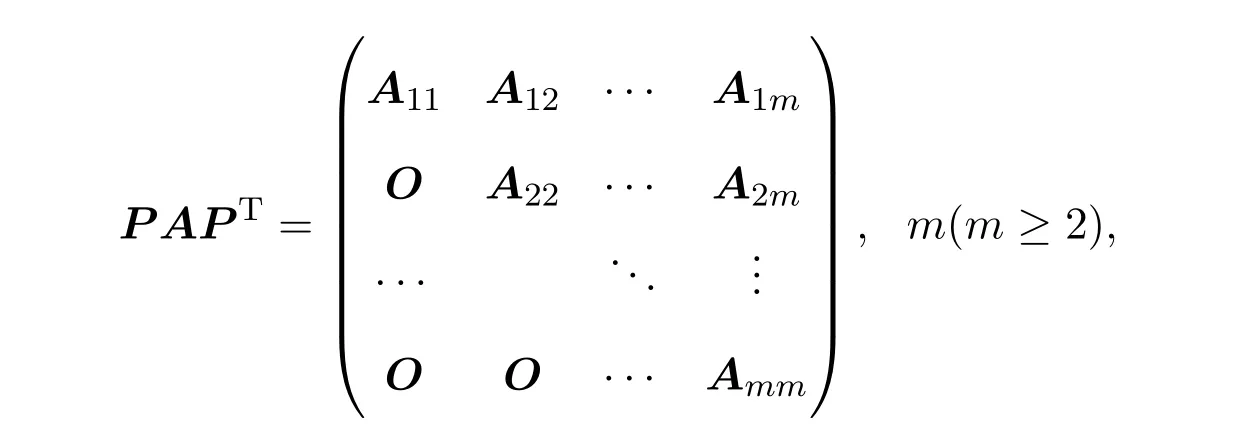
其中塊對角線上每塊Aii(1≤i≤m)或為不可約矩陣,或為一階零矩陣.顯然
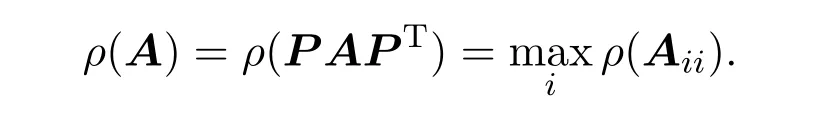
因此對非負可約矩陣,施行合適的置換變換后,同樣可以對其譜半徑進行估計.
3 數值算例
例3.1考慮非負矩陣

真值ρ(A)=5.74165738···.以下是參考文獻[1-9]和本文定理2.1關于矩陣A譜半徑估計的結果比較.
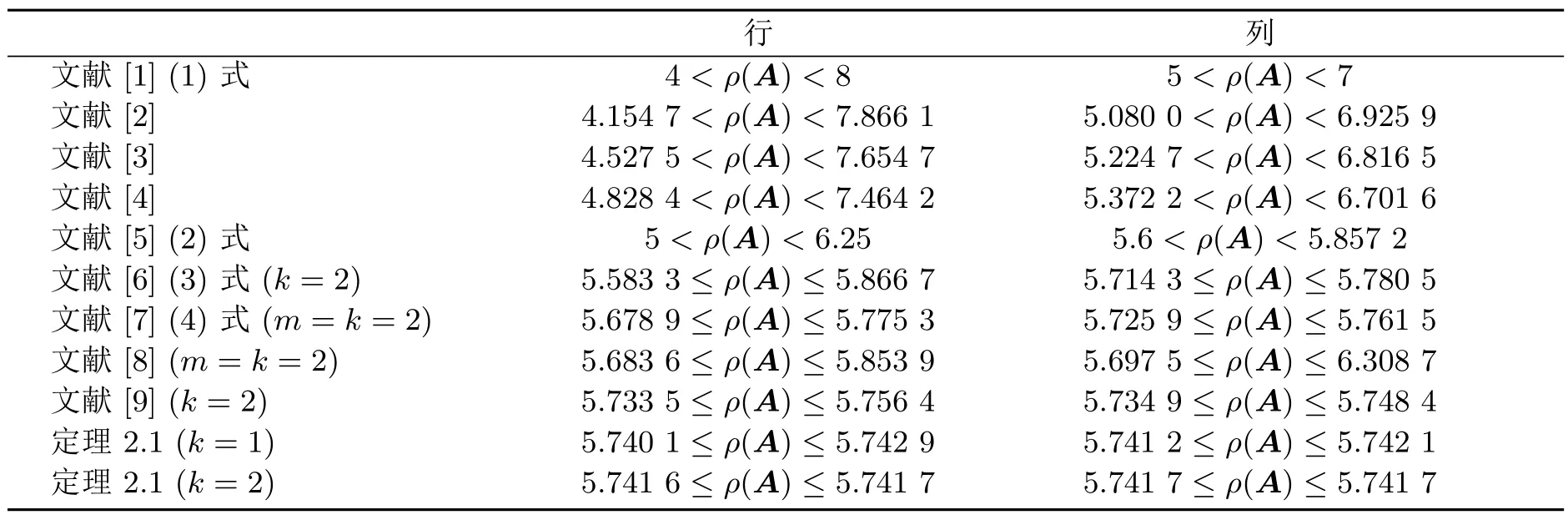
表1 譜半徑的界值比較
由表 1可以看出,定理 2.1得到的結論在一定程度上比現有的相關結果更精確,特別是k=2時,幾乎可以求得譜半徑的近似值
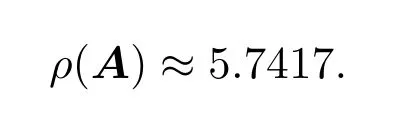
參考文獻
[1]Frobenius G.Uber Matrizen aus nichtnegativen Elementen,Sitzungsber[M].Berlin:Wiss,1912.
[2]Ledermannn W.Bounds for the greatest latent root of a positive matrix[J].London Math.Soc.,1950,25:265-268.
[3]Ostrowski A.Bounds for the greatest latent root of a positive matrix[J].London Math.Soc.,1952,27:253-256.
[4]Brauer A.The theorems of Ledermann and Ostrowski on positive matrices[J].Duke Math.,1957,24:265-274.
[5]Minc H.Nonnegative Matrices[M].New York:Wiley,1988.
[6]景何仿,尤傳華,司書紅.非負矩陣最大特征值的新界值[J].蘭州大學學報,2004,40(5):1-3.
[7]Liu S L.Bounds for the greatest characteristic root of a nonnegative matrix[J].Lin Alg App.,1996,(239):151-160.
[8]劉麗明,黃廷祝,劉小琴.非負矩陣最大特征值的新界值[J].電子科技大學學報,2007,36(2):343-345.
[9]殷劍宏.非負矩陣最大特征值的新界值[J].數值計算與計算機應用,2002,(4):292-295.
[10]鐘琴,周鑫,牟谷芳.非負矩陣Perron根的下界序列[J].純粹數學與應用數學,2016,32(4):331-336.
[11]錢茜,韓貴春.非負矩陣譜半徑的界[J].高等學校計算數學學報,2010,32(2):165-172.
New estimation for the spectral radius of nonnegative matrices
Zhong Qin
(Department of Mathematics,Sichuan University Jinjiang College,Pengshan 620860,China)
Estimation the bounds for the spectral radius of nonnegative matrices is important part in the theory of nonnegative matrices.It is more practical value when the bounds are expressed easily calculated function in element of matrix.New bounds for the spectral radius of nonnegative matrices were obtained by constructing two convergent sequences.Numerical example is given to illustrate the effectiveness by comparing with the relevant conclusions.
nonnegative matrices,spectral radius,upper bounds,lower bounds
O151.21
A
1008-5513(2017)02-0134-07
10.3969/j.issn.1008-5513.2017.02.004
2017-02-28.
四川省教育廳科研項目(13ZB0357);四川大學錦江學院青年教師科研基金(12130219)
鐘琴(1982-),碩士,講師,研究方向:矩陣理論及其應用的研究
2010 MSC:15A09

