基于EMD與果蠅參數尋優的LSSVM的機場能耗預測

王坤+江順之

摘 要： 針對機場能耗數據周期性、隨機性和非平穩時間序列性等特性，提出一種結合經驗模式分解（Empirical Mode Decomposition，EMD）和果蠅參數尋優的最小二乘支持向量機（Least Squares Support Vector Machines，LSSVM）的能耗預測方法。在原有LSSVM方法基礎上，運用EMD對天津機場能耗數據進行預處理，得到若干個本征分量。根據各分量的變化規律構造不同的最小二乘支持向量機模型分別預測，加入果蠅參數優化算法尋找最優的最小二乘支持向量機正則化參數與核函數參數。最后將各分量的預測結果疊加得到最終的預測值。仿真結果表明，經過EMD處理后各個分量突出了原能耗數據的特性，降低了預測的難度；果蠅參數尋優后能得到更加合適的正則化參數與核函數參數，提高了預測的精度。

關鍵詞： 機場能耗信息采集系統； 經驗模式分解； 果蠅參數優化； 最小二乘支持向量機； 組合預測

中圖分類號：TP181 文獻標志碼：A 文章編號：1006-8228（2017）04-35-06

Abstract： Focused on the periodic， random and non-stationary time series characteristics of Airport energy consumption data， an improved prediction algorithm based on empirical mode decomposition（EMD） and least squares support vector machine （LSSVM） with fruit fly parameter optimization is proposed. On the basis of the original LSSVM， decompose the data into multiple different intrinsic mode function components with EMD first， using fruit fly optimization algorithm to choose appropriate regularization parameter and kernel function parameters in LSSVM. And then depending on the each decomposition variation construct deferent least squares support vector machine model to predict respectively， and use fruit fly optimization algorithm to find the optimal regularization parameter and kernel function parameters. Finally， the superposition of each predicted result is the final forecast value. The simulation results with the three airport energy consumption prediction algorithms show that， the decomposition of data highlights the local characteristics of the original data after EMD， and fruit fly optimization algorithm gets better regularization parameter and kernel function parameters， thus has higher prediction accuracy.

Key words： airport energy information collection system； empirical mode decomposition； parameter optimization； least squares support vector machine； prediction

0 引言

進入二十一世紀以來，機場信息化發展迅速，研發了各類能耗信息管理系統，同時收集到了海量的機場能耗數據，這些數據可用于機場能耗預測。機場能耗預測是機場能源優化調度和綜合管理的前提。機場能耗預測精度越高，就越有利于提高機場大型用電設備的效率，同時能為后期的調度工作提供有效的數據支持[1]。

機場能耗數據具有隨機性、周期性、跳變性等特征，目前主流能耗預測方法是假設它為周期性的穩定序列，這導致分析數據特征的精度不高。為了更有效的掌握能耗序列變化的信息，運用經驗模式分解（EMD）方法對其進行數據預處理，再根據分解后各分量的特點完成后面模型建立和能耗預測。文獻[2]中提到EMD是一種將原序列的時域特性和頻域特性組合在一起分析的自適應信號分解方法，它將非平穩序列分解成若干個不同頻率的本征模態分量（Intrinsic mode function，IMF），各個分量包含不同的特征信息，對各分量分別進行分析可以減少了序列中不同特征信息之間的干涉或耦合[2]。

研究能耗預測的方法主要有回歸分析法[3]、時間序列法[4-5]、神經網絡法[6-9]等。其中神經網絡能耗預測法應用廣泛，但其計算速度緩慢、模型的網絡結構難以確定、容易陷入局部極小值而難以找到全局最優解，由此造成能耗預測精度不高[10]。支持向量機（SVM）算法其優點是結構簡單、學習速度快、全局最優、泛化性好，等優點一度被認為是神經網絡的替代方法，已在模式識別、函數估計和信號處理領域廣泛應用[11-12]。最小二乘支持向量機（LSSVM）改進了原有支持向量機求解的方法，所以具有更高效的計算速度和更高的預測精度，但在正則化參數與核函數參數選取方面仍存在盲目性問題，采用果蠅優化算法對LSSVM進行參數尋優可以有效提高模型的準確性，果蠅優化算法有程序簡潔，計算速度快，尋找最優解能力強，實用性強等優點。利用果蠅算法尋優能力強的優點對LSSVM算法進行改進，自動尋找最優的正則化參數與核函數參數。

本文將EMD與果蠅參數優化的LSSVM方法相結合，對機場能耗進行組合預測。先運用EMD對機場能耗數據進行數據預處理，將非平穩的機場能耗序列分解成不同頻率的本征模態分量的疊加。然后利用果蠅參數優化的最小二乘支持向量機對這些具有各自特征的分量進行分析。最后綜合有分量回歸的預測值得到最終的預測值。選取2012到2016年天津濱海國際機場部分站點的能耗數據為例，進行本文的方法應用。并將本文方法與未經EMD處理的果蠅參數優化LSSVM和未進行過果蠅參數優化的EMD-LSSVM方法進行對比分析，Matlab仿真結果表明本文方法有較高的預測精度。

1 機場能耗數據的采集

能耗數據來源于天津濱海國際機場的能源站監控系統。上位機是由VS2013和SQL2005聯合開發的一套數據采集與監控程序。機場各站點將采集到的能耗數據發送到互聯網，機場能源站上位機負責接受并儲存這些數據。系統結構圖如圖1所示。

2 經驗模式分解

機場能耗數序列具有復雜性、周期性、隨機性等特征。利用經驗模式分解（EMD）將機場能耗序列分解成若干個不同頻率的本征分量（IMF），IMF具如下特點：極值（極大值和極小值）數與過零點的數目相等或最多相差一個；在任意頻率里其上、下包絡線的均值必須是零[13]。原機場能耗序列經過EMD分解可以看出其周期項、隨機項、趨勢項，從而達到機場能耗序列平穩化的效果。具體的分解過程如下：

⑴ 根據原能耗序列X（t）的局部極值求出其上、下包絡線的平均值M1；

⑵ 將原能耗序列減去平均包絡后即可得一個去掉低頻的新序列F1=X（t）-M1；判斷F1是否滿足本征分量的條件，若不滿足將F1看作新X（t），重復上述處理過程，直到F1滿足為止，記F1為IMF1；

⑶ 將R1=X（t）-F1看作新的X（t），重復以上⑴和⑵步驟，即可依次得到IMF2，IMF3…直到Fn或Rn滿足給定的終止條件時篩選結束。最后，原始的數據序列X（t）可表示為：

式⑴表明，EMD處理之后原能耗序列X（t）分解成了幾個不同特征的分量，其中每個分量都代表一個特征尺度的能耗序列，對這些分量進行分析，可以降低后續建模的難度。

3 基于果蠅算法的正則化參數與高斯核函數的參數優化

對機場能耗數據進行EMD的數據預處理之后得到了若干個本征分量，根據各分量的變化特征采用參數優化的LSSVM方法分別進行建模。LSSVM可以有效克服算法計算量大，計算時間長等缺點，但是在正則化參數與核函數參數選取方面仍存在盲目性的問題，本文采用果蠅參數尋優的方法對LSSVM進行優化。具體推導過程如下：

LSSVM用如下函數形式對未知系統進行估計。

首先確定γ和σ的取值范圍，然后在取值范圍內隨機賦予若干個果蠅的初始位置，計算初始果蠅的味道濃度判定值并將其代入味道濃度判定函數即⑼式，找出濃度最低的果蠅，記下此時味道濃度最優的γ和σ以及濃度值并更新果蠅的位置，通過反復的迭代重復上述步驟，直到滿足跳出條件時得到一組最優目標值即最優的的γ和σ，將其代入式⑻得到最終的預測模型。

4 基于EMD和果蠅參數優化的LSSVM預測模型

利用EMD對能耗序列分解，分解后的本征分量突出了原能耗序列的局部特征，在此基礎上，根據各個本征分量的變化特點分別用參數優化的LSSVM算法建立不同的預測模型，利用果蠅參數尋優算法對正則化參數與高斯核函數參數進行尋優，以預測準確率最大為優化目標，設置跳出條件為兩代果蠅在一定限度之內，反復迭代直到找到最佳的正則化參數與核函數參數。因各個本征分量對最終的預測值貢獻有差異，最后將預測結果由SVM組合得到最終預測結果。其預測方法結構見圖2，步驟為：

⑴ 對能耗序列進行EMD分解得到n個IMF分量與一個余量Rn；

⑵ 對分解后的IMF分別建立合適的LSSVM能耗預測模型。

⑶ 設置果蠅參數尋優算法兩代果蠅味道濃度小于m時為迭代結束的跳出條件。

⑷ 將果蠅參數優化算法確定的正則化參數與高斯核函數的最優參數γ和σ代入式⑻中建立最終的數學模型。采用多個輸入、單輸出的一步預測方法；

⑸ 由于分解后的IMF分量特征相異，所以對最終結果影響存在差異，直接疊加會降低整體的預測精度，這里采用支持向量機加權組合的方法，通過支持向量機組合得到最終能耗預測值。

5 仿真實驗

數據來源于天津濱海國際機場能源站能耗數據，利用2012年1月1日至2016年1月1日整點天津濱海國際機場一號航站樓電能能耗數值，天氣狀況，節假日類型作為學習樣本，預測2016年9月31日全天機場電能能耗值。

采用相對誤差（Pe）和平均絕對百分比誤差（MAPE）作為評價最終的能耗預測的標準，如下式，其中pi為實際的能耗值，qi為預測的能耗值，N為預測值總個數。

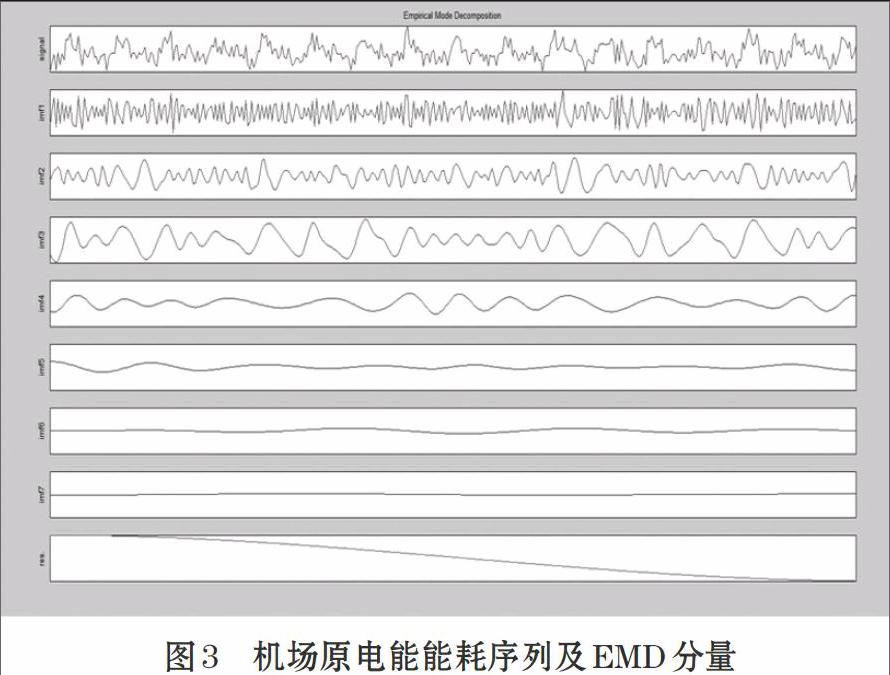
圖3給出航站樓電能能耗序列的EMD分解局部圖，得到七個IMF分量，可以看到IMF1為數值較小劇烈變化的高頻分量，IMF2與IMF3與原序列周期變化相似，IMF4到IMF7為數值較小低頻分量，R8為趨勢項。可以看到分解后的分量突出了原能耗序列的局部特征，能更明顯的看出原能耗序列的周期項、隨機項和趨勢項，能更好的把握能耗序列的特性。

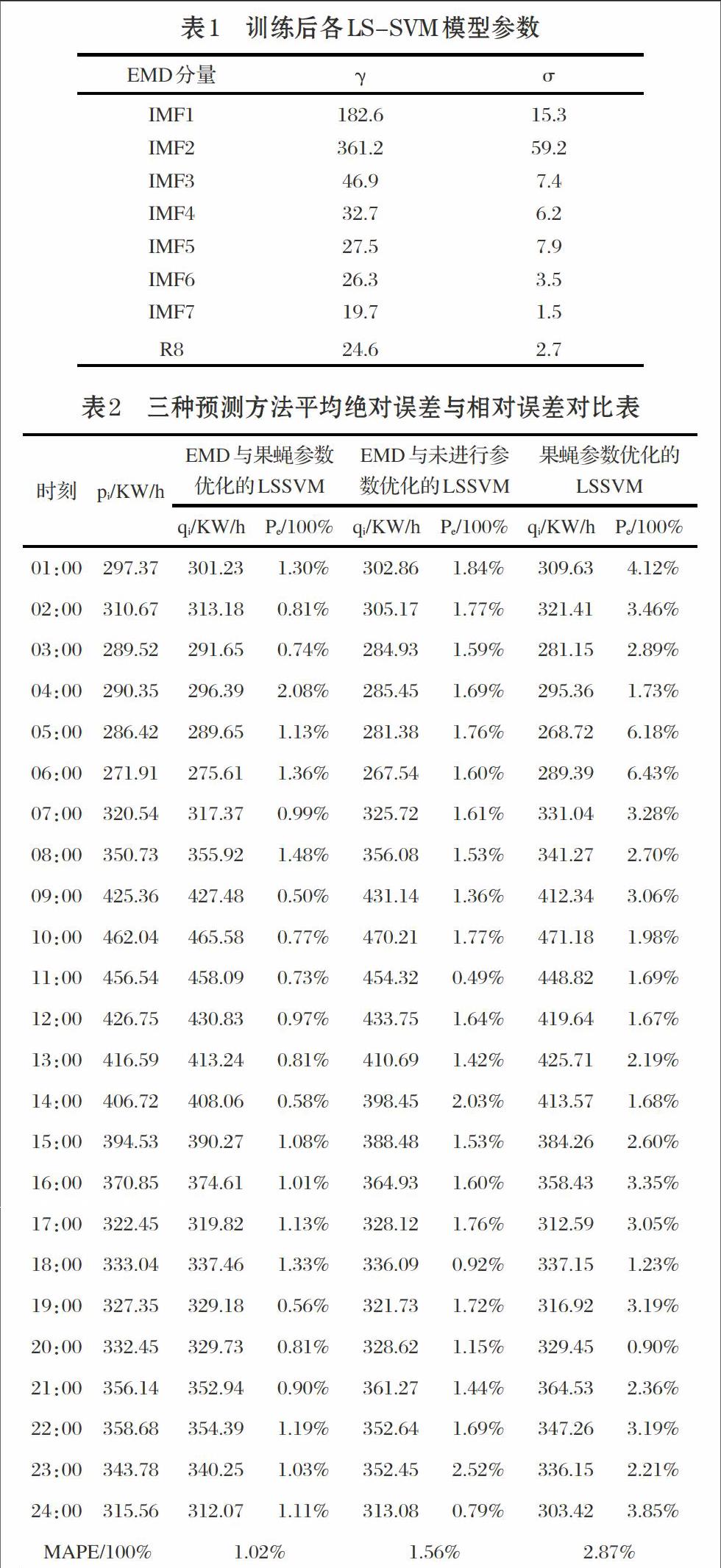
根據各分量的變化規律選用不同LSSVM模型，并利用果蠅算法進行參數尋優，其中果蠅種群數為3，種群規模為30，最大迭代次數為100，預測值與訓練值的均方差作為目標函數，以搜索最小均方差為目標，迭代結束時可得各個IMF的參數γ和σ如表1所示。

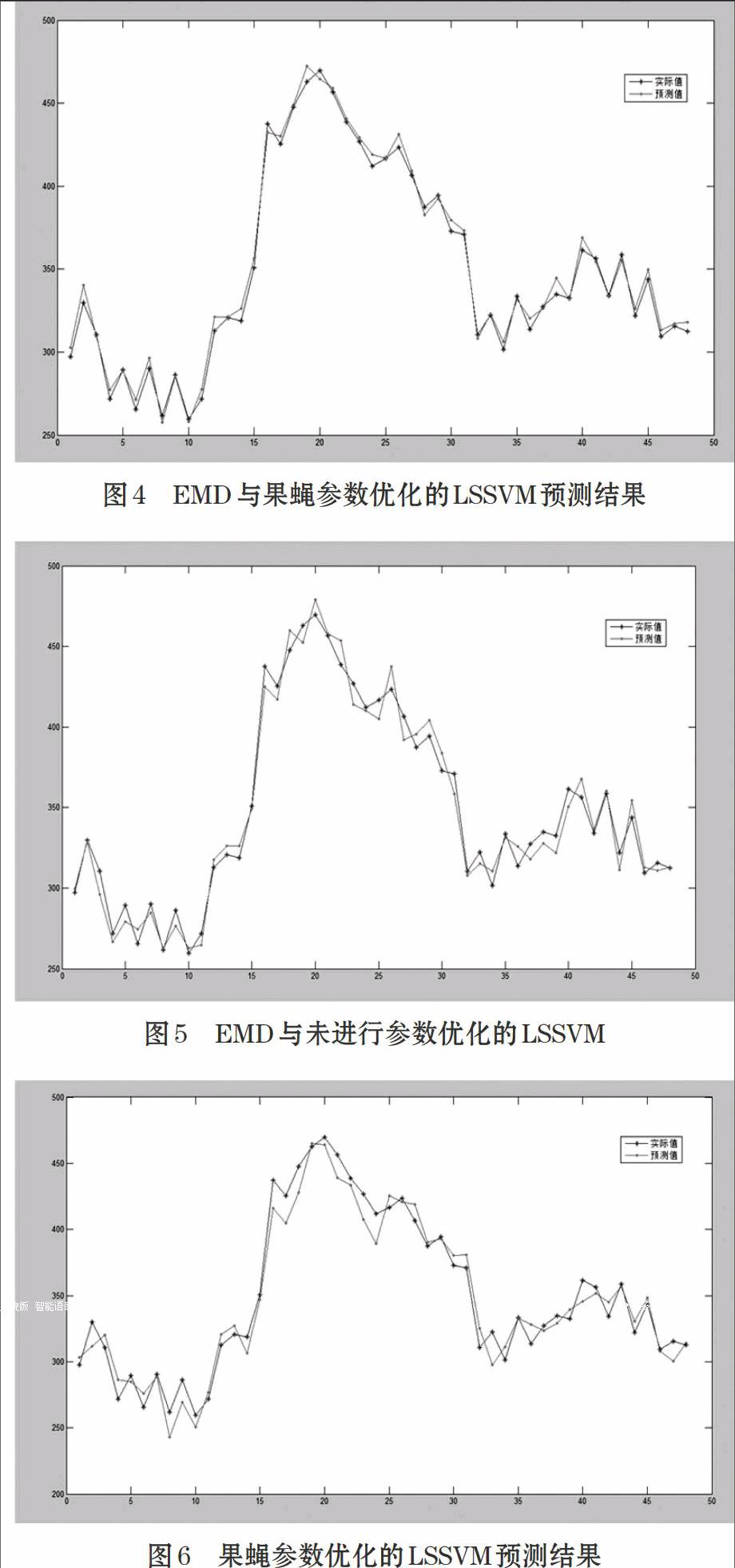
為了驗證本文方法的有效性，采用EMD與果蠅參數優化的LSSVM、 EMD和未進行參數優化的LSSVM、單一果蠅參數優化的LSSVM三種方法分別進行預測，三種方法的預測結果圖如圖4，圖5和圖6所示。可以看出本文方法的偏移實際值較大的點較少，預測曲線更平滑。其預測的平均絕對百分誤差和相對誤差的對比數據如表2所示。從三種方法的預測精度可以看出，EMD與果蠅參數優化LSSVM的平均絕對百分比誤差為1.02%，EMD與未進行參數優化的LSSVM的平均絕對百分比誤差為1.56%，而單一果蠅參數優化的LSSVM的百分比誤差為2.87%。本文方法在整點預測的相對誤差最小。

對比圖4，圖5。本文方法在分析機場能耗數據特征的基礎上，利用果蠅算法良好的全局尋優的能力對LSSVM的正則化參數γ與高斯核函數參數σ進行尋優。通過設定味道濃度判定函數和最優味道濃度的跳出條件，反復迭代不同的果蠅，直到迭代結束找出濃度最低的果蠅，得到最合適的正則化參數語高斯核函數參數γ和σ。相對于沒有進行參數優化的方法，合適的γ和σ使模型具有更佳的泛化和學習能力，使機場能耗的預測精度大幅提升，從表2可以看到本文的預測方法的相對誤差最大為1.02%最小則達到0.5%，從最終的預測曲線可以看出回歸函數更為平滑。

對比圖4，圖6。本文方法加入EMD后，將原本復雜機場能耗序列分解為一系列不同頻率的簡單的平穩分量，這些分量包含了原機場能耗序列的局部特征信息。隨著這些分量階數的提高，其隨機性減弱，對各個分量分別進行建模分析能更準確的把握原機場能耗序列的特征信息，使得能耗預測準確性大大提高。從最終的預測曲線可以看出，沒有加入EMD方法其預測效果誤差偏大，曲線偏移嚴重，而加入EMD之后預測準確性有顯著提高。

6 結束語

針對機場能耗數據的復雜性和隨機性造成預測精度不高的問題，本文提出EMD與果蠅參數優化的LSSVM預測方法。EMD分解可以分離出機場能耗序列的重要特征信息，根據分解之后各個分量的特點建立不同的最小二乘支持向量機子模型，然后利用果蠅算法良好的全局尋優能力進行關鍵參數的尋優，最后通過加權組合個分量的預測結果，得到最終預測結果。仿真結果表明，本文方法能進一步提高機場能耗預測的精度。未來研究工作將會對算法做進一步改進，加入實際數據的反饋，減少訓練樣本的添加影響，實現在線實時預測。

參考文獻（References）：

[1] 李永超.民用機場能源信息管理系統[D].北京交通大學碩士

學位論文，2010：1-6

[2] An X， J D， Zhao M， et al. Short-term prediction of wind

power using EMD and chaotic theory[J].Communications in Nonlinear Science and Numerical Simulation，2012.17（2）：1036-1042

[3] Lehmann A， Overton J M C， Leathwick J R. GRASP：

generalized regression analysis and spatial prediction[J].Ecological modelling，2002.157（2）：189-207

[4] 李瑞國，張宏立，王雅.基于量子粒子群優化算法的新型正交

基神經網絡分數階混沌時間序列單步預測[J].計算機應用，2015.35（8）：2227-2232

[5] Weigend A S. Time series prediction： forescasting the

future and understanding the past[M]，1994.

[6] 王德明，王莉，張廣明.基于遺傳 BP 神經網絡的短期風速預

測模型[J].浙江大學學報（工學版），2012.46（5）：837-841

[7] HUANG J， Luo H， WANG H， et al. Prediction of time

sequence based on GA-BP neural net[J]. Journal of University of Electronic Science and Technology of China，2009.5：029

[8] Jin W， Li Z J， Wei L S， et al. The improvements of BP

neural network learning algorithm[C]//Signal Processing Proceedings， 2000. WCCC-ICSP 2000. 5th International Conference on. IEEE，2000.3：1647-1649

[9] Yu S， Zhu K， Diao F. A dynamic all parameters adaptive

BP neural networks model and its application on oil reservoir prediction[J]. Applied mathematics and computation，2008.195（1）：66-75

[10] Junsong W， Jiukun W， Maohua Z， et al. Prediction of

internet traffic based on Elman neural network[C]//Control and Decision Conference， 2009. CCDC'09. Chinese. IEEE，2009：1248-1252

[11] Vapnik V. The nature of statistical learning theory[M].

Springer Science & Business Media，2013.

[12] 祝志輝，孫云聯，季寧.基于EMD和SVM的短期負荷預測[J].

高電壓技術，2007.33（5）：118-112

[13] Wu Z， Huang N E. Ensemble empirical mode

decomposition： a noise-assisted data analysis method[J]. Advances in adaptive data analysis，2009.1：1-41

[14] Comak E， Polat K， Güne? S， et al. A new medical

decision making system： least square support vector machine（LSSVM） with fuzzy weighting pre-processing[J].Expert Systems with Applications， 2007.32（2）：409-414

[15] 王坤，員曉陽，王力.基于改進型模糊支持向量回歸模型的

機場需求預測[J].計算機應用，2016.36（5）：1458-1463