基于RBF-ARX模型四旋翼飛行器的LQR控制方法*

劉麗麗 左繼紅 吳 軍

(1.中南大學信息科學與工程學院 長沙 410083)(2.湖南鐵道職業技術學院 株洲 412001)(3.長沙理工大學電氣與信息工程學院 長沙 410083)

基于RBF-ARX模型四旋翼飛行器的LQR控制方法*

劉麗麗1,2左繼紅1,2吳 軍1,3

(1.中南大學信息科學與工程學院 長沙 410083)(2.湖南鐵道職業技術學院 株洲 412001)(3.長沙理工大學電氣與信息工程學院 長沙 410083)

針對四旋翼欠驅動系統飛行過程中具有的非線性和強耦合性,提出了基于RBF-ARX模型四旋翼飛行器的LQR控制器設計方法。該法首先根據四旋翼飛行器的動力學特性構建四旋翼飛行器RBF-ARX的模型結構,并采用離線非線性參數優化方法辨識模型參數,獲取滿足工程精度需要的四旋翼非線性動態模型。然后,基于該模型設計了具有狀態反饋的四旋翼飛行器的LQR控制器,并通過求解工作點的Riccati方程,獲得狀態反饋矩陣。最后通過仿真和實時控制結果驗證了該方法的有效性和可行性。

四旋翼飛行器; 非線性; 姿態控制; 狀態反饋; 實時控制

1 引言

四旋翼飛行器的起飛和巡航是由四個螺旋槳配合完成的,通過改變各旋翼轉速,就能控制飛行姿態,具有結構簡單、操縱方便以及靈活機動等優點,通常被設計成無人駕駛的微型飛行器。廣泛用于野外航拍或飛行偵查等軍事領域,也用于建筑物內的導航與勘測等商業和民用領域。

實際應用中,四旋翼飛行器是一個多輸入多輸出的復雜非線性系統。目前絕大多數的研究,主要集中在非線性控制器的設計方面。文獻[1]采用PID控制策略和LQ控制策略實現四旋翼飛行器的控制[1]。文獻[2]提出了具有指數收斂特性的PD2反饋結構來補償飛行過程中的螺旋力矩[2]。文獻[3]提出了一種將魯棒非線性PI控制策略和backstepping技術相結合的方法[3],實現飛行器姿態控制。針對四旋翼飛行器的耦合問題,文獻[4]提出了一種動態逆策略[4]。為克服模型精確性和大風干擾對飛行器飛行姿態的影響,一些文獻討論了基于神經網絡的控制器設計方法[5～8]。

然而,這些方法大多基于系統物理模型進行設計的,但四旋翼在飛行過程中,不僅受到重力、空氣動力和陀螺效應等多種物理效應作用外,還受制于氣流等外部環境干擾[9～10],飛行器的精確物理參數無法得到,難以建立準確的物理模型,而模型的不精確又會給控制效果帶來不利的影響。使得傳統的基于物理模型的四旋翼姿態控制設計方法在實際應用時具有局限性。為了更好地描述四旋翼飛行器的非線性動態特性,可采用RBF-ARX模型的非線性建模方法。RBF-ARX模型是高斯徑向基函數網絡(RBF)和線性ARX(AutoRegressive model with exogenous variable)模型結構相結合的復合結構,是一種離線辨識的全局模型,兼具RBF網絡對非線性函數逼近精度高、學習速度快和ARX模型結構簡單、應用方便的優點,比較適合復雜非線性系統的控制問題,而LQR(linear-quadratic regulator)控制器是一種結構簡單、易于實現的基于模型的控制器。

為此,提出了一種基于RBF-ARX模型的自適應LQR控制方案。采用結構化非線性參數優化方法辨識模型參數,得到滿足工程精度要求的四旋翼非線性動態RBF-ARX模型。基于該模型通過求解工作點的Riccati方程,得到該區間內狀態反饋矩陣,設計了具有狀態反饋的LQR控制器,最終使得飛行器在其整個狀態空間內良好運行。

2 四旋翼飛行器控制系統

本文以四旋翼飛行器實驗平臺作為研究對象,型號是固高GHP3001,如圖1所示,采用GT-400-SV運動控制器,電機采24V5000RPM永磁直流電機,該物理平臺可以用來檢驗各種建模方法和控制算法在四旋翼飛行器中的應用。為保障飛行器運行過程中無損,固定了飛行器的三個自由度。其飛行動力由4個獨立直流電機帶動的相應旋翼提供,控制電機電壓可改變旋翼轉速,4個旋翼中有3個是水平放置的,它們決定飛行器的俯仰角pitch(繞Y軸旋轉)和翻轉角roll(繞X軸旋轉)輸出,這兩個輸出角范圍為-150～150(rad),還有一個豎直安裝,用來控制飛行器的巡航角yaw(繞Z軸旋轉),該輸出可以為任意角。該系統是一個具有4輸入3輸出的非線性耦合系統。對于飛行器來說基本的姿態控制包括飛行器的前進后退和左右平移。

3 RBF-ARX模型的辨識和結果分析

3.1 RBF-ARX模型結構

Deng等提出了一個離散時間線性時不變模型來逼近飛行器的連續時間非線性的動態模型[11],基于這個辨識模型設計了輸出狀態反饋控制器,本文嘗試用多個線性ARX模型來描述四旋翼飛行器的全局非線性模型,期望得到比物理模型更好的精度。對于多輸入多輸出的非線性系統,可將非線性區劃分若干局部線性區,局部線性區可采用式(1)的ARX模型來描述:

Y(t)=f(Y(t-1),…,Y(t-ka),U(t-1),…,

U(t-kb),V(t-1),…,V(t-kc))+ε(t)

(1)

其中:Y(t)∈Rn為輸出,U(t)∈Rm為輸入,ε(t)∈Rn為白噪聲序列,定義變量:

X(t-1)= [Y(t-1),…,Y(t-ka),U(t-1),…,

U(t-kb),V(t-1),…,V(t-kc)]T

(2)

模型(1)可寫成:

Y(t)=f(X(t-1))+ε(t)

(3)

模型(3)可以看成是一個具有函數系數的ARX模型,可看出,模型(3)的依存于狀態的函數系數問題實際上是一個函數逼近問題,即將多維輸入空間X轉換成一維的向量空間wi=πi(X)。可采用神經(RBF)網絡逼近非線性矢量函數的方法,RBF網絡描述非線性系統動態特性效果優良。對于多變量的四旋翼飛行器的RBF-ARX模型描述如下:

(4)

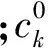
(5)

(6)

確定一組合適的狀態矢量,可將式(6)轉換成狀態空間模型,定義狀態變量如下:

確定式(6)中的w(t)后,其對應的局部線性狀態空間模型方程為

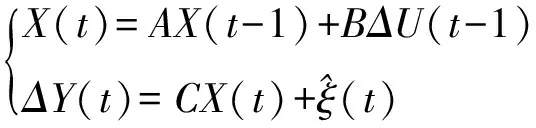
(7)

其中:

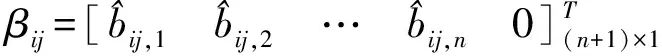
χ=[1 0 … 0]1×(n+1)

3.2 系統模型的辨識和結果分析

為了驗證RBF-ARX模型的有效性,采樣四旋翼飛行器在基于物理模型LQR控制的實時運行的全局數據來辨識和測試模型。四旋翼飛行器RBF-ARX模型的階次可利用比較AIC值的方法來選取。針對研究本體,AIC計算方法為[12]

(8)

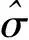
圖2 俯仰角實際輸出與模型輸出結果

圖2～圖4所示為四旋翼飛行器采用RBF-ARX模型后對測試數據的建模結果。圖2中,y1(t)、ym1(t)分別為飛行器俯仰角實際輸出和模型輸出,error1代表俯仰角實際和期望輸出的誤差,單位是rad,histogram1代表應殘差直方圖反映誤差的分布情況。同理,圖3和圖4分別代表翻轉角和巡航角模型輸出精度,顯然,RBF-ARX模型下系統實際輸出能很好的跟隨期望輸出,誤差波動范圍小且成高斯狀分布,表明模型比較理想,建模精度優良,能很好地描述飛行器系統的全局非線性動態特性。

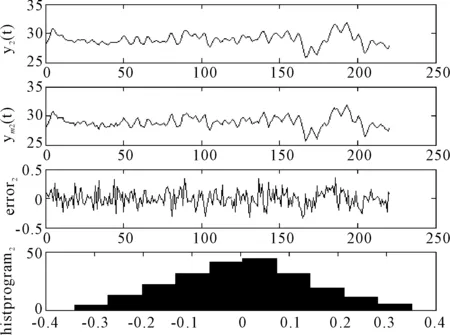
圖3 翻轉角實際輸出與模型輸出結果

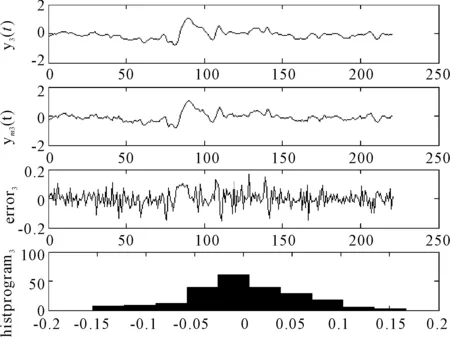
圖4 巡航角實際輸出與模型輸出結果

4 基于RBF-ARX模型的LQR控制策略和控制結果分析

4.1 基于RBF-ARX模型的LQR控制策略

根據圖5局部線性狀態空間LQR控制器的設計思路,利用多變量RBF-ARX模型可以方便地在任意工作點處局部線性化的優點,采用基于局部線性ARX模型設計LQR控制器的方法,設計出了基于局部線性狀態空間模型的無限時間狀態調節器。

圖5 基于RBF-ARX模型LQR控制器結構圖

由于多變量RBF-ARX模型是一個時變全局非線性模型,所以,基于多變量RBF-ARX模型的全局LQR控制器,實際上是一種基于局部線性化模型的無限時域預測控制器。引入最優控制的性能指標作為目標函數,即設計一個輸入量ΔU(k),使得

(9)

為最小,其中Q>0,R>0分別為對狀態變量和輸入變量的加權矩陣,表示目標函數中動態偏差和控制作用的相對重要性。相對較大的權,意味著對目標函數中對應項的較大限制。據實際要求為實現對系統的最佳控制,需在輸出控制輸出間找尋一個最優平衡點。使得如上性能指標最小化,可由Riccati方程在某個工作點求解P:

-pA-ATp+pBR-1BTp-Q=0

(10)

得到對稱定常矩陣P,進而得到該工作點處的狀態反饋增益矩陣:

K=R-1BTA-T(P-Q)

(11)

最后得到在該工作點處的狀態反饋最優控制律

(12)

4.2 基于RBF-ARX模型LQR實時控制結果

通過RBF-ARX模型的辨識及仿真結果已經看出其卓越的建模精度,基于RBF-ARX模型的全局LQR控制策略不僅在局部工作區間控制精確,在全局工作區間具有很強的自適應性,因為基于RBF-ARX模型的全局LQR控制策略可看成是由多個局部線性模型和多個局部LQR控制器組成,在相鄰兩個釆樣點處控制器的控制率的變化具有平滑連續性。通過實時控制實驗進一步說明該方法的優越性。圖5～圖6為基于RBF-ARX模型的LQR控制器的實時控制結果,為進一步證明該模型的優越性,將基于ARX模型的LQR控制器的實時控制結果(圖8所示)進行對比。

圖6和圖7分別是四旋翼飛行器基于RBF-ARX模型的實時控制輸出和輸入曲線,圖6中括號內的三個值分別是俯仰角、翻轉角和巡航角的控制目標值,箭頭指定控制目標的時間區間,實線是俯仰角(PITCH)變化曲線,虛線是翻轉角(ROLL)變化曲線,點線是巡航角(YAW)變化曲線。

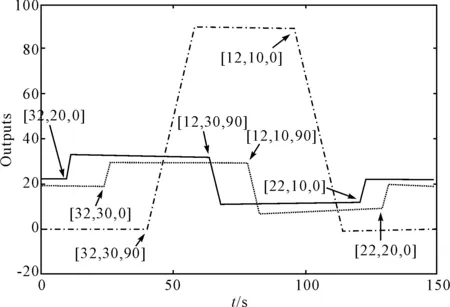
圖6 基于RBF-ARX模型的實時控制輸出曲線

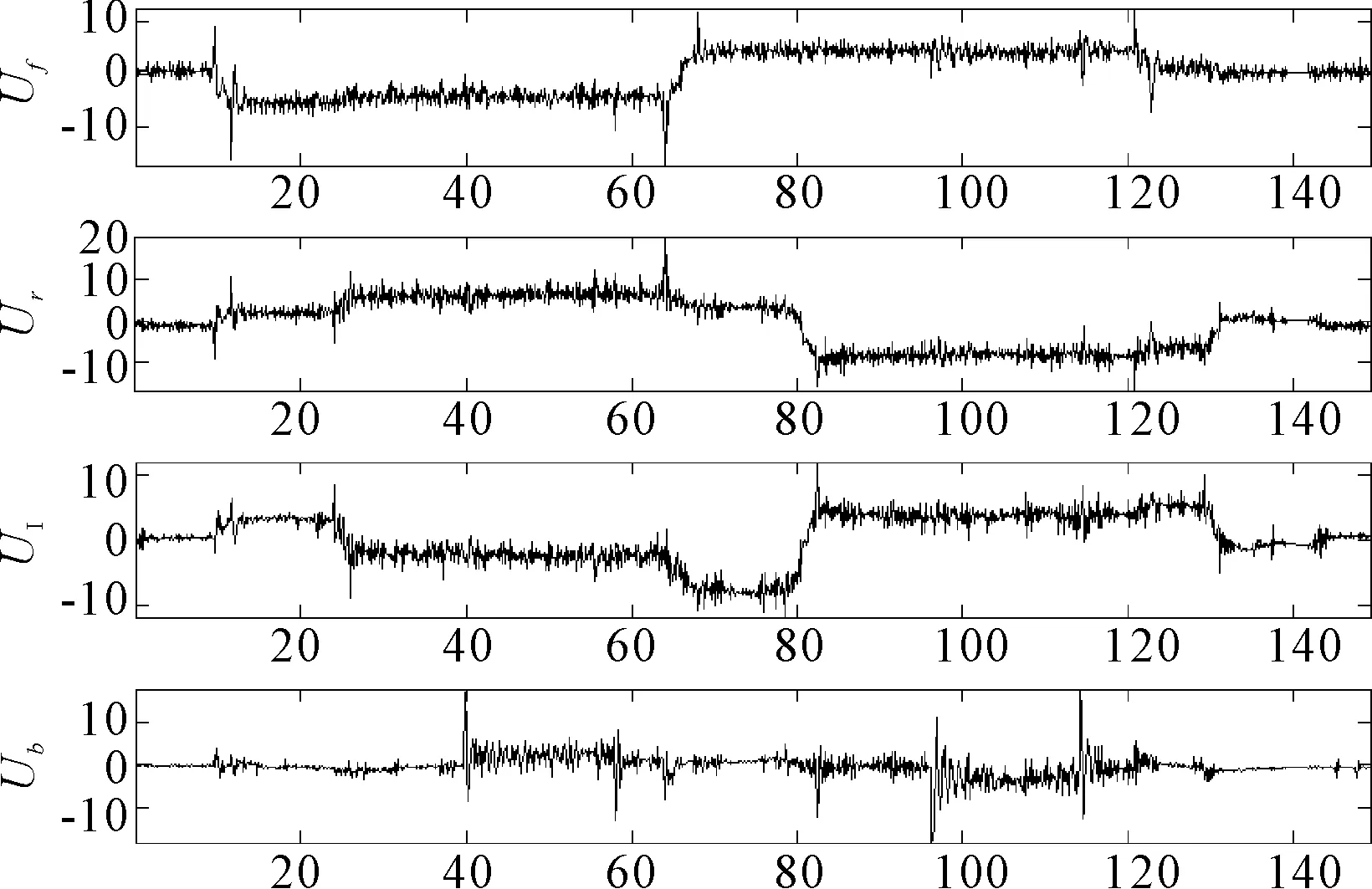
圖7 基于RBF-ARX模型的實時控制輸入曲線

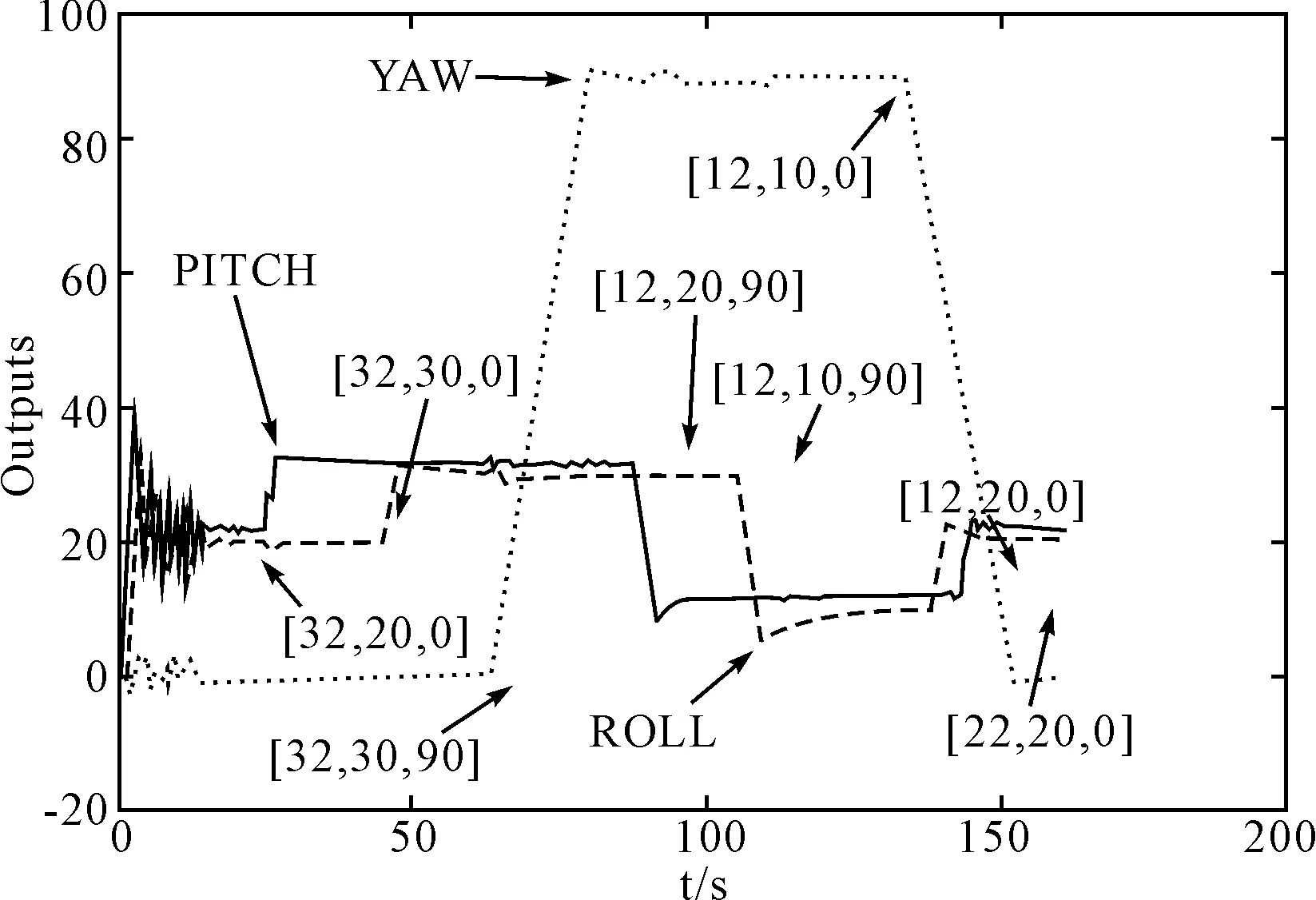
圖8 基于ARX模型LQR實時控制輸出結果

圖6中四旋翼首先處于水平懸停姿態,即:俯仰角(p)、翻轉角(r)和巡航角(y)分別為22、20和0;在10s處,控制俯仰角由初始值22變為32,保持翻轉角和巡航角不變;在40s處,控制翻轉角由初始值20變為30,保持俯仰角和巡航角不變;在70s處,控制巡航角由初始值0變為90,保持俯仰角和翻轉角不變;根據控制目標依次分別改變三個輸出角,維持一段時間后,控制四旋翼飛行器達到另一目標飛行姿態,并保持一段時間,最終使四旋翼飛行器回到初始水平懸停狀態。圖6曲線顯示,初始懸停狀態就很穩定,沒有抖動和超調,當輸出姿態角按照控制目標分別變化時,動態過程響應迅速,并且幾乎沒有超調,穩定后輸出非常平穩,基本沒有震蕩和超調。

為進一步證明RBF-ARX模型的優越性,對比圖8所示的基于ARX模型的LQR控制器的實時控制結果,可看出該模型下盡管穩態振蕩和超調不是很大,但初始狀態有很大的震蕩,由此可見,基于RBF-ARX模型的實時控制更勝一籌。

為證明基于RBF-ARX模型的LQR控制策略具有更強的適應性,控制3個輸出根據目標在同一時刻改變飛行姿態,并保持一段時間,最終恢復初始水平懸停姿態。圖9和圖10分別顯示了基于物理模型和RBF-ARX模型下完成同一控制目標的效果。從圖9所示的基于物理模型的LQR實時控制曲線可以看出,在初始水平懸停姿態,輸出曲線有較大的震蕩;飛行器目標姿態突然變化后,雖然動態響應迅速,但超調較大,穩定到新姿態后穩態特性尚可;穩定一段時間重新回到初始水平懸停狀態,輸出曲線又出現了存在較大超調和振蕩。原因是物理模型參數不夠精確,是一個簡化的模型,并且旋翼的非線性動態特性被簡化為線性,無法保證在所有姿態下的控制都表現良好。

圖9 基于物理模型的LQR實時控制效果

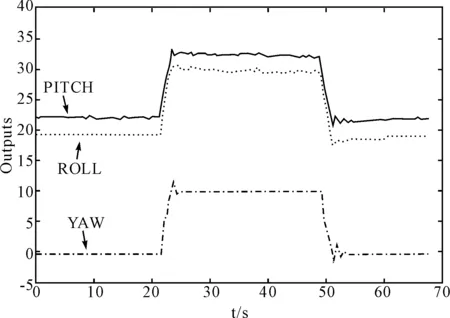
圖10 基于RBF-ARX模型組的LQR實時控制效果

圖10為基于ARX模型組的LQR實時控制曲線,相比圖9,該建模及控制方法取得了較好的控制效果。在初始懸停位置,輸出曲線震蕩在很小幅度內,到達穩態后基本平穩,沒有出現大幅震蕩現象;控制輸出姿態角突然變化后其動態反應迅速,超調量明顯比基于物理模型的控制策略小得多;回到初始水平懸停姿態后,并未出現大的振蕩和超調現象。

總之,基于RBF-ARX模型的LQR控制器在非線性的四旋翼飛行器的應用效果十分顯著,該方法在實際工程應用領域是可行的。

5 結語

針對非線性和強耦合的四旋翼飛行器,提出了一種基于RBF-ARX模型的LQR控制方法。通過建立該模型并采用離線的方法辨識參數,通過仿真分析證實該模型具有較高精度。基于該模型設計了雙閉環狀態反饋LQR控制器,實際上是一種基于局部線性化模型局部控制器的無限時域預測控制器,通過實時控制結果分析,該方法控制效果顯著,并與基于物理模型和ARX模型的控制結果對比,結果顯示,基于RBF-ARX模型的LQR控制方法控制效果更佳,從而證實該方法的有效性和卓越性。

[1] Bouabdallah S, Noth A, Siegwart R. PID vs LQ Control Techniques Applied to an Indoor Micro Quadrotor[C]//Proceedings of the IEEE International Conference on Intelligent Robots and Systems. Sendai, Japan,2004:2451-2456.

[2] Tayebi A, McGilvray S. Attitude stabilization of a VTOL quadrotor aircraft[J]. IEEE Transactions on Control Systems Technology,2006,14(3):562-71.

[3] Bouchoucha M, Tadjine M, Tayebi A, et al. Step by step robust nonlinear PI for attitude stabilisation of a four-rotor maniaircraft[C]//16th Mediterranean Conference on Control and Automation. Ajaccio,2008:1276-1283.

[4] Das A, Subbarao K, Lewis F. Dynamic inversion with zero-dynamics stabilisation for quadrotor control[J]. IET Control Theory & Applications,2009,3(3):303-314.

[5] Guenard N, Hamel T, Mahony R. A Practical Visual Servo Control for an Unmanned Aerial Vehicle[J]. IEEE Transactions on Robotics,2008,24(2):331-340.

[6] Morel Y, Leonessa A. Direct adaptive tracking control of quadrotor aerial vehicles[C]//Florida Conference on Recent Advances in Robotics, Miami, Florida,2006:1-6.

[7] Nicol C, Macnab C, Ramirez-Serrano A. Robust neural network control of a quadrotor helicopter[C]//Canadian Conference on Electrical and Computer Engineering,2008:1233-1238.

[8] Dierks T, Jagannathan S. Neural network output feedback control of a quadrotor UAV[C]//47th IEEE Conference on Decision and Control. Cancun,2008:3633-3639.

[9] Dunfied J, Tarbouchi M, Labonte G. Neural network based control of a four rotor helicopter[C]//IEEE International Conference on Industrial Technology,2004:1543-1548.

[10] 朱君.四旋翼無人飛行器控制系統設計及控制方法研究[D].呼和浩特:內蒙古科技大學碩士學位論文,2012. ZHU Jun. Design and control method for the control system of four rotor unmanned aerial[D]. Huhhot: Master’s degree thesis of technological University of Inner Mongolia,2012.

[11] Deng X, Schenato L, Sastry S. Mode1 identification and attitude control for a Micromechanical flying insect including thorax and sensor models[C]//Proceedings of IEEE International Conference on Robotics and Automation,2003:1152-1157.

[12] 秦宣云,卜英勇,夏毅敏.基于AIC準則優化的徑向神經網絡微地形曲面重構[J].中南大學學報(自然科學版),2004(10):815-819. QIN Xuanyun, BU Yingyong, XIA Yimin. Micro terrain surface’s reconstruction based on the RBF neural network of AIC criterion optimization[J]. Journal of Central South University(Natural Science Edition),2004(10):815-819.

LQR Control for A Quad-Rotor Helicopter Based on RBF-ARX Mode

LIU Lili1,2ZUO Jihong1,2WU Jun1,3

(1. School of Information Science and Engineering, Central South University, Changsha 410083)(2. College of Hunan Railway Professional Technology, Zhuzhou 412001)(3. School of Electrical and Information Engineering, Changsha University of Science & Tehcnology, Changsha 410083)

For the quad-rotor helicopter which is nonlinear and coupled with each other, the design of LQR controller on quad-rotor helicopter based on RBF-ARX mode are discussed. The structure of the quad-rotor helicopter’ RBF-ARX model based on dynamic properties is built firstly, and the model parameters is identified using the off-line nonlinear parameter optimization methods, the quad-rotor helicopter’s nonlinear dynamic model is obtained to meet the demand of engineering precision.then, the state feedback ‘s LQR controller based on the model is given, and by solving the Riccati equation of working point, the state feedback matrix is accessed. Finally, the simulation results and real time attitude control verify the validity and feasibility of the proposed method.

quad-rotor helicopter, nonlinear, attitude control, state feedback, real time control Class Number TP391.9

2016年10月13日,

2016年11月11日

2015年度國家自然科學基金“抗參數橫揺的欠驅動船舶航跡跟蹤控制研究”(編號:61403045);2015年度湖南省教育廳科學研究資助項目“四旋翼飛行器的建模及控制策略的研究”(編號:15C0903)資助。

劉麗麗,女,碩士研究生,講師,研究方向:復雜非線性系統建模及控制方法。左繼紅,男,碩士研究生,講師,研究方向:復雜非線性系統建模及控制方法。

TP391.9

10.3969/j.issn.1672-9722.2017.04.014