分數階Duffing振子的組合共振
顧曉輝 楊紹普 申永軍 劉進志


摘要:研究了2個諧波激勵作用下含分數階微分項的Duffing振子的一類組合共振,利用多尺度法得到了2ω1+ω2型組合共振的一次近似解析解,分析了定常解的穩定性。應用奇異性理論研究了幅頻響應分岔方程,得到了開折參數平面的轉遷集和所有區間上分岔曲線的拓撲結構。最后通過數值仿真分析了系統參數對組合共振幅頻響應的影響。研究表明:分數階微分項即具有阻尼特性又具有剛度特性,選擇合理的分數階微分項參數可以有效改善系統的響應特性。
關鍵詞:Duffing振子;分數階微分;組合共振;多尺度法;奇異性理論
中圖分類號:0322;0313
文獻標志碼:A
文章編號:1004-4523(2017)01-0028-05
DOI:10.16385/j.cnki.issn.1004-4523.2017.01.004
引言
分數階微積分發展至今已有超過300年的歷史,近些年來,基于眾多學者在其定義、性質、計算方法等方面的不懈努力,分數階微積分正逐步由抽象的數學概念走向工程應用,尤其在描述黏彈性材料本構關系方面和控制工程領域深受關注。
在動力學方面,目前主要集中于含分數階微積分項的動力系統振動特性的研究,wahi應用平均法研究了含分數階阻尼項的非線性時滯系統的響應特征,發現了一些分數階系統的特有現象。shen提出了等效線性阻尼和等效線性剛度的概念,分析了含分數階微分項的線性、非線性振子的動力學響應。Rossikhin基于R-L定義,應用多尺度法推導了Duffing振子的二階近似解,并指出了一些學者的錯誤觀點。Du研究了一類分數階微分方程的初值問題及其求解方法。GUO提出一種改進的諧波平衡法得到了分數階Van der Pol振子的近似解析解。楊建華應用諧波平衡法分析了一類分數階線性系統在周期信號激勵下系統響應的近似解。chen、孫春燕研究了隨機激勵作用下分數階Duffing振子的幅頻特性。廖少鍇結合Newmark法和Zhang-Shimizu法推導了分數階微分項的數值計算方法,并研究了含平方非線性分數階振子的動力學行為。cao采用數值積分法,結合相圖、龐加萊截面圖、分岔圖等分析了分數階阻尼對系統動力學性能的影響。
通過以上分析可發現,現有文獻大多針對單頻激勵或隨機激勵展開討論,而在實際問題中,許多工程結構或部件會受多頻激勵作用的影響,多頻激勵作用下的系統具有更復雜的動力學特性。
4.系統參數的影響
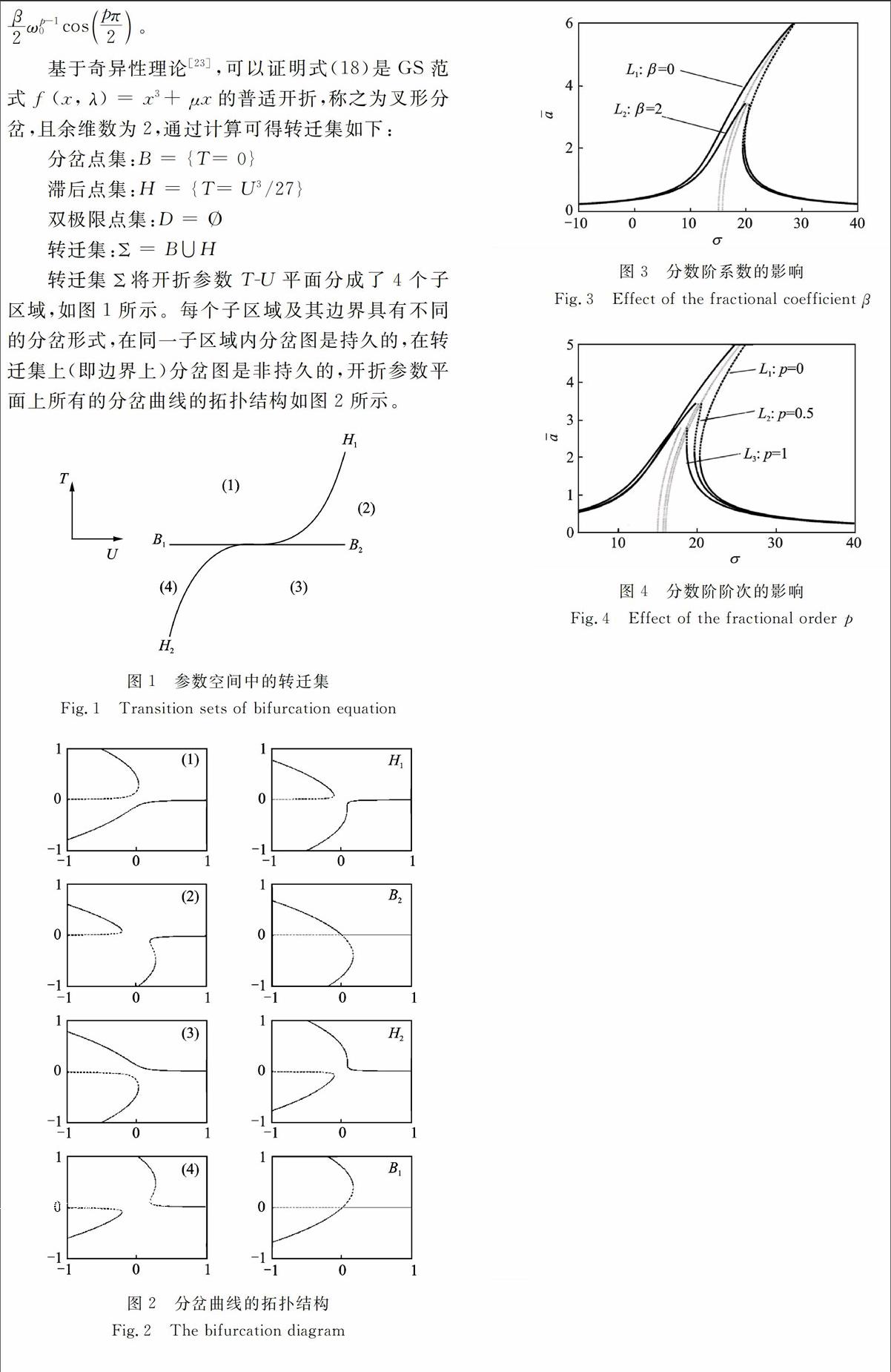
在上述分析中,開折參數落在不同的區域內,系統有不同的動力學行為,可以為系數設計提供理論指導。然而開折參數并不是獨立的系統參數,而是系統參數的組合,下面通過分析系統的幅頻響應研究系統參數的影響。
選取一組基本參數u=1,ωo=1,α=1,β=2,p=0.5,B1=1,B2=2。根據式(13)可以得到系統響應的幅頻曲線如圖3中L2所示,其中實線為穩定解,虛線為不穩定解,點線為骨架曲線。無分數階微分項(即β=0時)的整數階系統響應的幅頻曲線如圖3中L1所示。通過對比可以發現,分數階微分項既影響了系統的剛度特性,使骨架曲線右移,共振頻率增大,又影響了系統的阻尼特性,使共振峰值減小,即分數階微分項既具有剛度特性又具有阻尼特性,對系統的幅頻響應有重要影響。
圖4給出了分數階微分項階次對系統幅頻響應的影響。通過對比可以發現,p=0時,系統具有最大的共振頻率和共振峰值,即系統的等效剛度最大,等效阻尼最小;而p=1時,系統具有最小的共振頻率和共振峰值,即系統的等效剛度最小,等效阻尼最大。說明當分數階階次p→0時,分數階微分項幾乎等同于線性剛度的作用;當p→1時,分數階微分項幾乎等同于線性阻尼的作用,這與分數階微分項的本質保持一致。
圖5和6給出了線性阻尼系數和非線性項系數對系統幅頻響應的影響。從圖中可以看出,與整數階系統類似,線性阻尼系數并不影響幅頻曲線的彎曲程度,只影響共振峰值的大小,阻尼越大,峰值越小。而非線性項系數既影響共振頻率又影響共振峰值,非線性項系數越大,幅頻曲線越彎曲。與分數階項系數不同的是,通過加大非線性項系數,不會改善系統的響應特性。
5.結論
本文應用多尺度法和奇異性理論分析了2個諧波激勵作用下含分數階微分項的Duffing振子的一類組合共振,得到了系統的一次近似解,分析了定常解的穩定性。基于幅頻響應,得到了系統穩態響應分岔方程的轉遷集和對應的分岔圖。通過數值仿真分析了系統參數對幅頻特性曲線的影響,研究表明:分數階微分項即具有阻尼特性又具有剛度特性,選擇合理的分數階微分項參數可以有效改善系統的響應特性。

