二次頻率耦合的對(duì)角切片譜分析
李奕瑤 劉建新 劉偉渭 王開云


摘要:三階累積量對(duì)角切片譜可以識(shí)別二次相位耦合關(guān)系,抑制不存在耦合的頻率成分,由于此優(yōu)良的性質(zhì),對(duì)角切片譜在信號(hào)分析領(lǐng)域得到了廣泛的應(yīng)用。然而,二次相位耦合的定義要求原始信號(hào)同時(shí)滿足頻率耦合和相位耦合的關(guān)系,這樣的信號(hào)在實(shí)際中幾乎不存在,很多文獻(xiàn)把取得較好分析效果的原因歸結(jié)于對(duì)角切片譜具有識(shí)別二次相位耦合的能力,這是不嚴(yán)謹(jǐn)?shù)摹L岢龅亩晤l率耦合的概念,相比于二次相位耦合,二次頻率耦合對(duì)信號(hào)的相位沒有要求。通過理論推導(dǎo)證明了對(duì)角切片譜能夠識(shí)別僅存在頻率耦合關(guān)系的信號(hào),從而提升了二次相位耦合理論的實(shí)用性。最后,通過分析具有內(nèi)圈故障的滾動(dòng)軸承振動(dòng)信號(hào),對(duì)提出的二次頻率耦合理論進(jìn)行了驗(yàn)證。
關(guān)鍵詞:信號(hào)分析;二次相位耦合;二次頻率耦合;對(duì)角切片譜;變階累積量
中圖分類號(hào):TN911.6
文獻(xiàn)標(biāo)志碼:A
文章編號(hào):1004-4523(2017)01-0135-05
DOI:10.16385/j.cnki.issn.1004-4523.2017.01.018
引言
數(shù)十年來,一階統(tǒng)計(jì)量(如均值、方差)和二階統(tǒng)計(jì)量(如自相關(guān)函數(shù)、功率譜)被廣泛應(yīng)用于機(jī)械振動(dòng)信號(hào)的分析,但這些方法理論上只適用于分析線性和高斯信號(hào)。在實(shí)際應(yīng)用中,需要從更高的階次上反映信號(hào)特征。相比于一、二階統(tǒng)計(jì)量,高階統(tǒng)計(jì)量具有能夠抑制高斯噪聲、辨識(shí)非最小相位系統(tǒng)、檢驗(yàn)信號(hào)非線性等優(yōu)點(diǎn)。然而,高階統(tǒng)計(jì)量分析的缺點(diǎn)也較為鮮明,其計(jì)算量較大,且計(jì)算量隨階數(shù)的增加進(jìn)一步增大,難以實(shí)現(xiàn)較大數(shù)據(jù)量的實(shí)時(shí)計(jì)算。為此,出現(xiàn)了累積量切片的方法,常見的切片包括水平方向切片、垂直方向切片、對(duì)角方向切片等。在累積量切片中,使用得最多的是三階累積量對(duì)角切片,它既顯著地減小了三階累積量的計(jì)算量,又保留了三階統(tǒng)計(jì)量的諸多優(yōu)點(diǎn),這些優(yōu)點(diǎn)可概括如下:
(1)若x(t)為一高斯信號(hào),那么它的三階累積量對(duì)角切片譜Sx(ω)=0。這表明對(duì)角切片譜可抑制高斯噪聲。
(2)若x(t)的概率密度函數(shù)服從對(duì)稱分布,那么它的三階累積量對(duì)角切片譜Sx(ω)=0。這說明對(duì)角切片譜可以抑制對(duì)稱分布的噪聲。
(3)若x(t)=p(t)+q(t),p(t)和g(t)相互獨(dú)立,q(t)為高斯信號(hào),那么Sz(ω)=Sp(ω)。這意味著對(duì)角切片譜可以用來分離加性非高斯信號(hào)與高斯噪聲。
(4)對(duì)角切片譜能夠識(shí)別二次相位耦合關(guān)系、抑制獨(dú)立頻率分量。
相對(duì)于正常工作狀態(tài),當(dāng)機(jī)械系統(tǒng)出現(xiàn)故障時(shí),會(huì)產(chǎn)生一種特殊的非線性現(xiàn)象,最常見的表現(xiàn)為:兩個(gè)頻率成分相互作用,產(chǎn)生一個(gè)和頻和(或)一個(gè)差頻,與此同時(shí),對(duì)應(yīng)的相位也滿足這種和或差的關(guān)系。這一現(xiàn)象被稱為二次相位耦合。簡單地說,信號(hào)中含有三個(gè)成分,其頻率和相位分別為fk和φk(k=1,2,3),如果同時(shí)滿足f3=f1+f2和s=φ1+φ2,或同時(shí)滿足f3=f1-f2和φ3=φ1-φ2,就稱為二次相位耦合。
二次相位耦合的定義要求信號(hào)同時(shí)滿足頻率和相位的關(guān)系,但在實(shí)測(cè)的機(jī)械振動(dòng)信號(hào)中,能滿足這種要求的信號(hào)非常罕見。文獻(xiàn)[8-11]將成功實(shí)現(xiàn)特征提取、故障識(shí)別歸因于優(yōu)點(diǎn)(4),這種結(jié)論是不合理的。本文研究發(fā)現(xiàn),在實(shí)際的應(yīng)用中對(duì)相位進(jìn)行限制是沒有必要的,相位的取值并不會(huì)對(duì)對(duì)角切片譜的識(shí)別能力造成影響,為此本文提出二次頻率耦
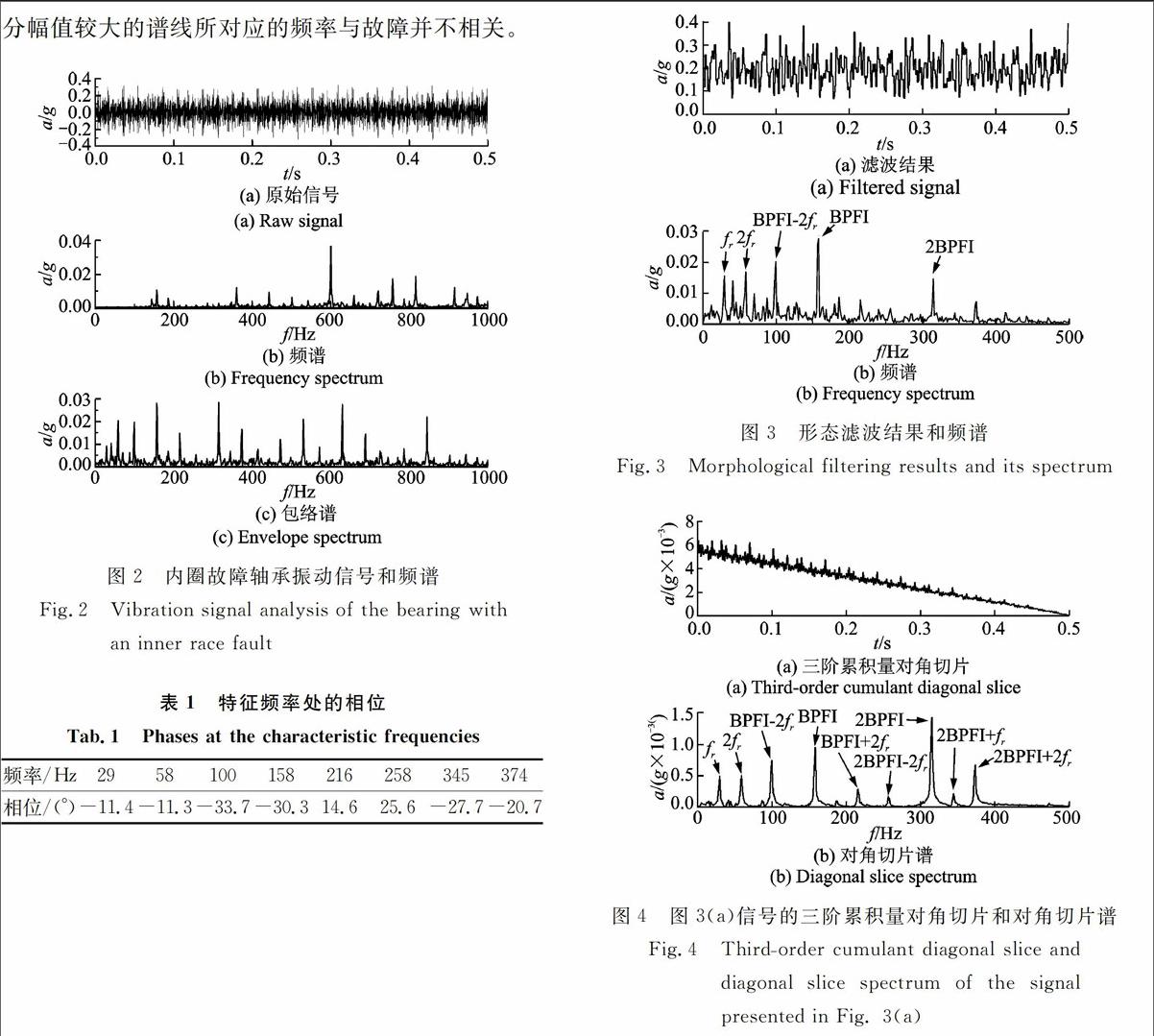
對(duì)圖2(a)所示信號(hào)進(jìn)行數(shù)學(xué)形態(tài)學(xué)濾波[16-18],其濾波結(jié)果和對(duì)應(yīng)的頻譜如圖3所示。濾波后信號(hào)的三階累積量對(duì)角切片如圖4(a)所示,對(duì)角切片譜如圖4(b)所示。從對(duì)角切片譜中可以看轉(zhuǎn)頻(fr)及其2倍頻(2fr),內(nèi)圈故障頻率(BPFI)及其2倍頻(2BPFI),還有一些邊頻,如:BPFI-2fr,BPF1+2fr,2BPFI-2fr,2BPFI+2fr和2BPFI+fr,這些頻率清晰的表明軸承內(nèi)圈存在故障。需要指出的是,上述頻率(29,58,100,158,216,258,345,374Hz)之間均存在耦合關(guān)系,如158=100+58,216=158+58,等等。而不存在頻率耦合關(guān)系的成分完全被清除,使得圖4(b)的對(duì)角切片譜顯得非常“干凈”,故障特征突出。對(duì)比圖4(b)和圖3(b)可知,圖4(b)結(jié)果中所展示的良好的特征頻率提取效果與對(duì)角切片譜能夠有效識(shí)別二次頻率耦合的能力密切相關(guān)。
通過計(jì)算可得上述特征頻率位置的相位,如表1所示。可見,在這些發(fā)生頻率耦合的地方,對(duì)應(yīng)的相位并不存在耦合關(guān)系。這再次證明,對(duì)角切片譜可以識(shí)別僅具有二次頻率耦合的信號(hào),且對(duì)角切片譜中的幅值也較為明顯,并未受到相位的影響。根據(jù)表1,對(duì)角切片譜“干凈”的重要原因并不是文[8-11]中所稱的二次相位耦合,而是二次頻率耦合。
5.結(jié)論
二次相位耦合要求信號(hào)同時(shí)滿足頻率耦合和相位耦合的條件,但在實(shí)際的機(jī)械振動(dòng)信號(hào)中,這樣苛刻的條件很難滿足,幾乎無法找到如此特殊信號(hào)。因此,二次相位耦合的理論難以得到實(shí)際的應(yīng)用。而本文提出的二次頻率耦合理論對(duì)信號(hào)的相位不作要求,只需滿足頻率上的耦合關(guān)系。通過理論推導(dǎo)證明了對(duì)角切片譜能夠識(shí)別二次頻率耦合關(guān)系、抑制獨(dú)立頻率分量,且幅值的差異不會(huì)影響分析判斷。最后通過對(duì)具有內(nèi)圈故障的滾動(dòng)軸承的分析,證明了在相位不滿足耦合關(guān)系時(shí),對(duì)角切片譜依然能提取故障特征。

