均布荷載作用下槽鋼繞弱軸的非線性彎曲

袁偉斌，包兆水，詹 偉(浙江工業(yè)大學 建筑工程學院，浙江 杭州 310014)

均布荷載作用下槽鋼繞弱軸的非線性彎曲

袁偉斌，包兆水，詹 偉
(浙江工業(yè)大學 建筑工程學院，浙江 杭州 310014)

主要通過能量法研究了有限長的簡支槽鋼梁繞弱軸的彎曲響應，其中的基本假設是受均布荷載作用的薄壁鋼梁的總應變能分析可以簡化為兩個階段，第一個階段是腹板和翼緣的局部彎曲響應(板的行為)，第二個階段是截面扁化變形后薄壁鋼梁的整體彎曲響應(梁的行為).通過最小勢能原理推導均布荷載作用下槽鋼梁非線性失穩(wěn)的理論解，同時還研究了腹板中部增設縱向加勁肋對槽鋼梁的非線性彎曲響應的影響.并運用ANSYS對不同尺寸槽鋼梁進行了幾何非線性分析，結果顯示理論解和有限元解之間能夠很好的吻合.利用Simitses的方法研究了受沖擊均布荷載作用的簡支槽鋼梁繞弱軸彎曲的動力失穩(wěn)，討論了跨度對槽鋼梁臨界彎矩和非線性彎曲響應的影響.

槽鋼梁；均布荷載；扁化變形；非線性失穩(wěn)；有限元

冷彎薄壁構件不同于傳統(tǒng)的混凝土構件，其常被用作檁條、屋架和墻柱等受彎或受壓構件并且其壁厚較薄且桿件較細長，所以相對于強度問題來說，應更加重視其穩(wěn)定問題.近年來，國內(nèi)外學者對于薄壁鋼構件進行了大量的研究，Magnucki等[1]提出了薄壁槽鋼梁整體和局部屈曲的解析解，描述了其翹曲函數(shù)與翹曲慣性矩，并利用有限元法對其彈性屈曲的理論解進行了數(shù)值計算和實驗驗證.Luo等[2]根據(jù)廣義梁理論，用兩種計算模型分析了薄壁卷邊槽鋼梁繞弱軸彎曲的畸變屈曲臨界應力.Shifferaw等[3]提出了一種預測冷彎薄壁型鋼構件發(fā)生局部、畸變或側(cè)扭屈曲模式時的非彈性抗彎承載力的方法，對在非彈性階段的儲備能力進行檢討，并提供了其非彈性階段抗彎承載力的簡化表達式.Rogac等[4]對開口冷彎薄壁構件在土木結構工程中的應用進行了分析，根據(jù)歐洲規(guī)范對開口冷彎薄壁構件的實際應用進行了分析，給出了其工程使用的意見和建議.Vale?[5]分析了不同長細比的薄壁箱梁在軸壓下的承載力，用ASNYS對其進行了非線性分析，并與設計承載力標準值進行了比較.Bedair[6]提出了一種計算箱型截面腹板剪切屈曲的解析表達式，并用半解析有限條法進行了驗證.褚云朋等[7]對冷彎薄壁方鋼管受壓長柱進行了試驗研究與有限元計算分析.考察了長細比變化時，試件的破壞模式、荷載—位移曲線以及承載力等的變化情況.姚行友等[8]對冷彎薄壁型鋼矩形空心管構件進行了軸壓試驗研究，分析了構件的屈曲模式和極限承載力，并用采用ABAQUS有限元程序進行了計算.袁偉斌和徐潔等[9]從能量法入手對彎矩作用下兩端簡支角鋼梁的屈曲性能進行了研究.趙滇生等[10]對蜂窩梁的強度和剛度進行了研究.王森軍等[11]研究了影響蜂窩梁撓度的因素.袁偉斌等[12]從理論上研究了純彎作用下蜂窩梁的側(cè)向扭轉(zhuǎn)屈曲，并提出了不同邊界條件下的臨界荷載解析解.

現(xiàn)在為止，冷彎薄壁構件的非線性研究還不夠深入和全面，特別是考慮截面扁化變形對構件彎曲響應影響的非線性分析十分稀少.針對上述情況，提出了利用改進的Brazier方法研究均布荷載下有限長槽鋼梁繞弱軸非線性彎曲響應.并考察了梁跨度對其非線性彎曲響應的影響.其次，運用Simitses的方法研究了動力均布荷載作用下槽鋼的動力失穩(wěn).考察了腹板縱向加勁肋對槽鋼梁繞弱軸的非線性彎曲響應的影響.最后使用有限元方法，利用ANSYS對相應尺寸的槽鋼梁模型進行了幾何非線性分析，驗證理論的準確性.

1 槽鋼物理模型和基本公式

考察如圖1所示的一根腹板受均布荷載作用的薄壁槽鋼梁，其邊界條件為兩端簡支.一般情況下作用于橫向的均布荷載主要是由剛度較大的部分承受，而上頂面在受到垂直于面的荷載作用時變形較兩棱邊的變形更大，從而大部分荷載轉(zhuǎn)移至腹板與翼緣交線處.所以為了簡化模型與分析，將均布荷載簡化為兩條作用于腹板與翼緣交線處的均布線荷載.在均布荷載的作用下，槽鋼會發(fā)生繞弱軸的彎曲，腹板將受到壓縮.隨著均布荷載的增加，由于Brazier效應的存在，槽鋼腹板將會發(fā)生扁化變形，并且兩側(cè)的翼緣線隨之發(fā)生相應的旋轉(zhuǎn)，截面扁化變形如圖2(b)所示.因此，薄壁槽鋼梁繞弱軸彎曲時的變形可以分為兩部分：一部分是槽鋼梁的跨度方向的整體彎曲變形(梁形式的彎曲)，另一部分是槽鋼截面的扁化變形.而對于腹板增設縱向加勁肋的槽鋼梁來說，在進行能量分析中，主要是在局部分析階段中增加了縱向加勁肋產(chǎn)生的附加局部彎曲應變能和在整體分析階段中增加了梁截面的剛度而增加了其整體彎曲應變能.

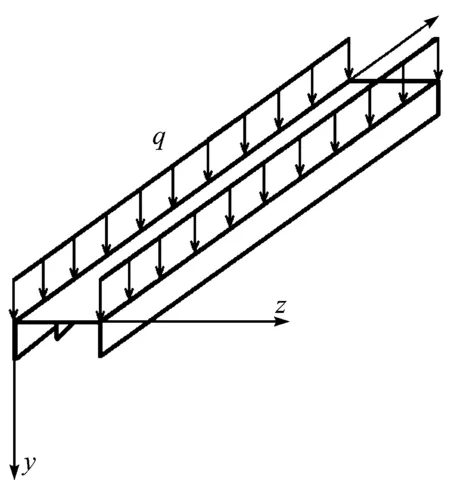
圖1 槽鋼梁簡化計算模型Fig.1 Simplified computing model of channel-section beams

對于一根受均布荷載作用的薄壁槽鋼梁，定義跨度方向為x軸，橫截面尺寸以及坐標系位置如圖2所示.當槽鋼腹板受到均布荷載作用發(fā)生的扁化變形，可以假定槽鋼腹板在截面位移的變形遵循受均布荷載作用時簡支梁的撓度函數(shù)，而由于邊界效應的影響，沿著梁跨度方向(x軸方向)的截面扁化變形是不一致的，可以假設腹板在長度方向的變形為一個正弦半波，因此腹板局部位移函數(shù)可以設為

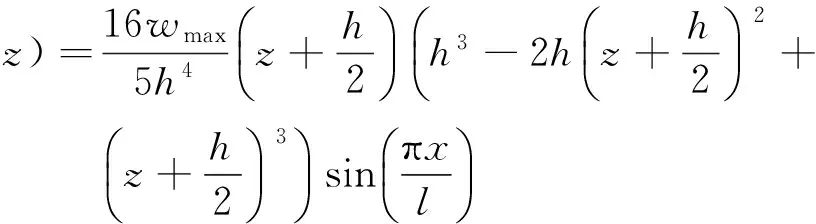
(1)

式中：q為均布荷載值；E為材料的楊氏模量；I為腹板截面的慣性矩；h為腹板的寬度；l為槽鋼的跨度；令wmax為腹板截面中點處的局部最大位移(相對于腹板兩邊).

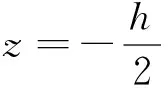
(2)

對于薄壁槽鋼梁整體而言，則其撓度方程可以假設為

(3)

式中：A為一個連續(xù)的常數(shù)；l為槽鋼梁的跨度.

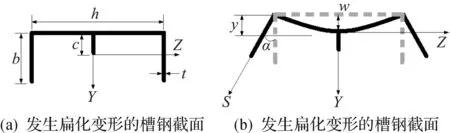
圖2 帶肋槽鋼截面幾何尺寸Fig.2 Geometry of channel section with stiffener

根據(jù)總應變能假設，槽鋼梁彎曲時的總應變能由兩部分組成：第一部分是局部變形的彎曲應變能，第二部分是截面發(fā)生扁化變形的槽鋼梁沿跨度方向的整體彎曲應變能.

利用式(1)所示的槽鋼腹板局部位移函數(shù)w(x,z)，根據(jù)板殼理論的知識可知腹板發(fā)生彎曲變形產(chǎn)生的應變能可表示為

(4)

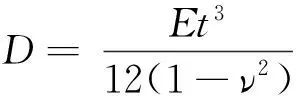
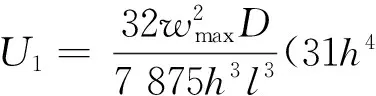
(5)

若槽鋼腹板中線處增設縱向加勁肋，則其產(chǎn)生的附加彎曲應變能為

(6)

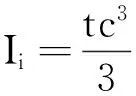
(7)

式(7)即為縱向加勁肋的局部變形應變能.而由于縱向加勁肋的存在，截面發(fā)生變形的槽鋼梁延跨度方向的整體彎曲應變能可以表示為

(8)

值得注意的是，式(8)中Iw是考慮了截面扁化變形的槽鋼梁慣性矩，根據(jù)圖2(b)所示變形，其慣性矩可以表示為

(9)

(10)

注意到腹板截面中點處的局部最大位移wmax相對于式中其他物理量來說是一個極小的量，所以將式(1)分別代入式(9，10)后所得的兩項表達式中可以省略wmax的高次項，并表示為

(11)

(12)

值得注意的是，如果截面不發(fā)生變形即wmax=α=0，那么此時Iw將收斂于未發(fā)生扁化變形的槽鋼慣性矩，即圖2(a)截面的慣性矩.

將槽鋼梁整體彎曲撓度函數(shù)式(3)和截面發(fā)生變形的槽鋼梁慣性矩式(11)代入式(8)，可以得到槽鋼梁整體彎曲應變能為

(13)

由能量守恒定律可知，系統(tǒng)的總勢能為槽鋼的總應變能減去均布荷載的外力勢能.則均布荷載的外力勢能可以表示為

(14)

式中q為腹板受到的均布荷載值.系統(tǒng)的總勢能可以表示為

Π=U1a+U1+U2-W

(15)

2 靜態(tài)槽鋼非線性彎曲響應

受均布荷載作用的薄壁槽鋼梁由于截面扁化變形而引起的非線性彎曲響應可以通過求解板組的非線性彎曲方程組或利用能量法得到.經(jīng)驗表明利用能量法來求解薄壁槽鋼梁的非線性彎曲響應更為方便.因此，可以通過利用最小勢能原理和勢能駐值原理來求解槽鋼梁受均布荷載作用下的非線性彎曲響應，可以計算為

(16)

(17)

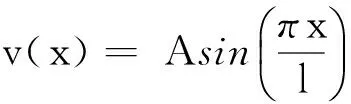
要求解處槽鋼梁在發(fā)生躍越失穩(wěn)時的臨界均布荷載荷載值，可利用的變分公式為

(18)

將式(15)代入式(18)，并且聯(lián)立非線性方程組(16，17)，就可以求得臨界均布荷載qcr，槽鋼梁臨界彎曲狀態(tài)時的連續(xù)常數(shù)A和腹板中點的局部最大位移wmax，即

(19)

(20)

(21)

由式(19～21)可知：當縱向加勁肋深度c=0時，即為非加勁槽鋼梁的屈曲參數(shù)表達式.

3 有限元分析

在對槽鋼梁進行靜態(tài)屈曲有限元分析中，材料的屬性統(tǒng)一采用如下定義：楊氏模量E=206 GPa，泊松比v=0.3.使用shell143殼單元建立有限元模型，這是一種四節(jié)點的彈性小應變殼單元.由于研究的槽鋼梁是受均布荷載作用的，并且邊界條件為兩端簡支，所以整個槽鋼梁模型是關于跨中截面對稱的，因此在進行有限元幾何非線性分析時，可以取槽鋼梁的一半來進行建模分析.以此提高計算效率而且便于觀察彎曲時構件的變形.為了對比有限元分析結果和理論解，故加載情況按簡化計算模型的加載形式作用.

為了驗證以上理論解的正確性，利用有限元軟件ANSYS對在均布荷載作用下繞弱軸彎曲的簡支槽鋼梁進行了幾何非線性分析.選取截面尺寸為h=140 mm,t=1.5 mm，b=50 mm的槽鋼進行考察，槽鋼梁的跨度為l=2 000 mm和l=3 000 mm兩種，加勁肋深度取c=0 mm和c=20 mm，結合有限元和理論解析解得到彎矩—撓度曲線圖，如圖3，4所示.由圖3，4可以看出：當不增設縱向加勁肋時(圖3)，盡管理論曲線預測的跨中最大撓度比有限元結果略大；當腹板中線增設縱向加勁肋時(圖4)，理論曲線的臨界彎矩值比有限元非線性分析得到的臨界彎矩值略小，但是理論曲線預測的臨界彎矩與有限元非線性分析得到的臨界彎矩十分吻合(誤差在5%內(nèi)).還可以看出：當跨中撓度較小時，理論曲線與有限元曲線幾乎完全吻合，只有當彎矩值接近臨界彎矩時理論曲線才與有限元曲線產(chǎn)生微小誤差.該誤差可能是由于在理論分析中僅使用了應變位移方程的線性項，而省略了其非線性項.并且在有限元非線性分析中不僅考慮了截面扁化變形的因素，還綜合考慮了其他的因素，比如說變形引起的薄膜力和薄壁結構的翹曲等.但是這些因素在理論分析中是沒有考慮在內(nèi)的，這也可能是引起誤差的原因.盡管如此，但是從圖3，4中依然可以看出截面的扁化變形是影響槽鋼梁彎曲響應和引起躍越失穩(wěn)的主要因素.

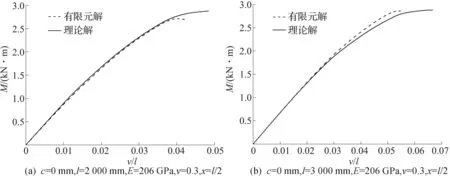
圖3 槽鋼梁彎矩—撓度的理論曲線與有限元曲線對比Fig.3 Comparison of moment-displacement curves between present and finite element analyses (channel-section beams)

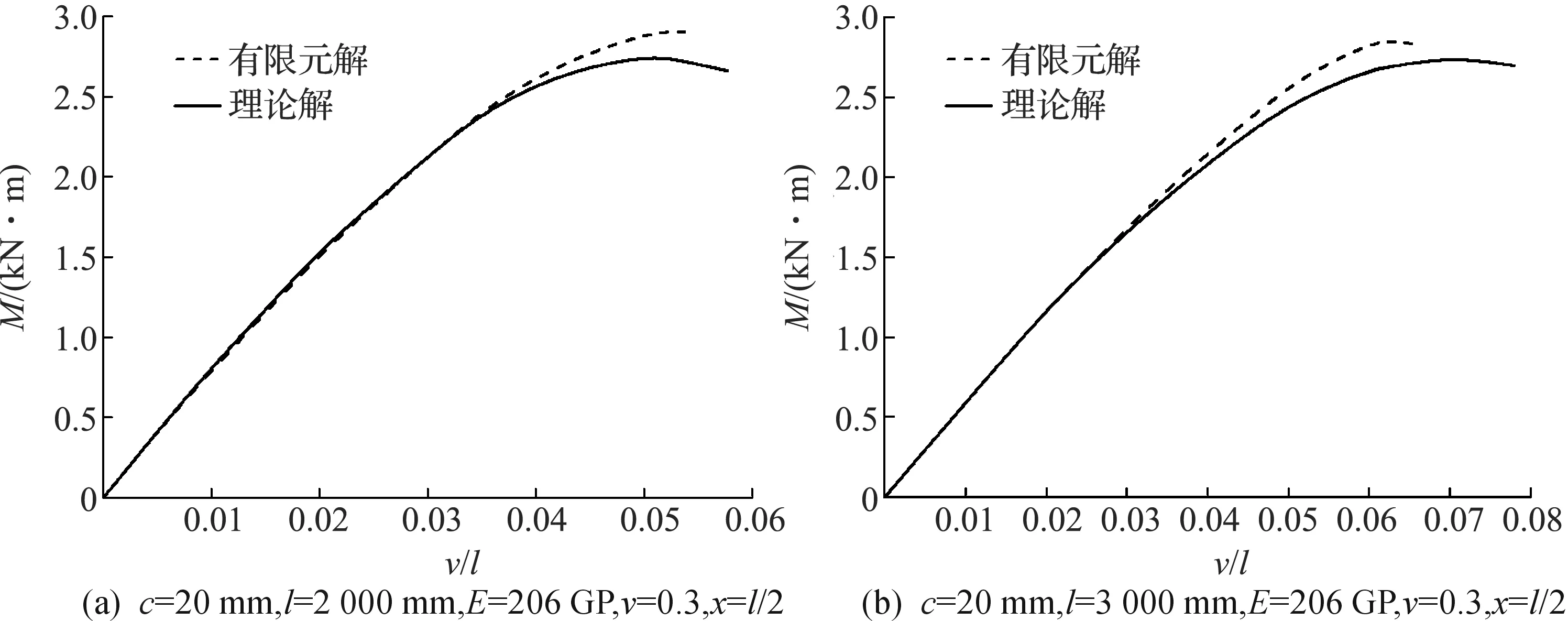
圖4 帶肋槽鋼梁彎矩—撓度的理論曲線與有限元曲線對比Fig.4 Comparison of moment-displacement curves between present and finite element analyses (channel-section beams with stiffener)

同時，以槽鋼梁長細比為橫坐標，以臨界彎矩(Mcr=qcrl2/8)為縱坐標，將不帶肋槽鋼梁的理論解與有限元解均繪制在圖中，同時與無限長槽鋼受純彎作用繞弱軸彎曲時的理論臨界彎矩[13]進行對比分析.圖5表示的是隨著梁長細比的增加臨界彎矩的變化，正如所預測的一樣，當隨著梁長細比的增加，其臨界彎矩不斷減小.根據(jù)圖5顯示當長細比l/i(i為截面的回轉(zhuǎn)半徑)很小的時候，由于此時的邊界效應的影響很大，所以曲線較為陡峭.當長細比l/i很大的時候，曲線將趨近其在跨度無限長情況下的臨界彎矩.值得注意的是，與文獻[13]的理論臨界彎矩相比，可以看出均布荷載作用下槽鋼梁的臨界彎矩略大于純彎作用下的臨界荷彎矩，這反應了梁的彎矩梯度對臨界彎矩的影響，在文獻[14]中也提出非純彎作用構件的抗彎承載力往往比純彎作用下的要高出10%～20%.

為了考察腹板縱向加勁肋深度對槽鋼梁非線彎曲相應的影響，針對截面尺寸為h=140mm,b=50mm,t=1.5mm，跨度為2m的槽鋼梁，增設c=20mm，c=24mm，c=28mm的三種不同深度的加勁肋進行分析(圖6)，從圖6中可以看出：臨界彎矩和臨界彎矩所對應的撓度都隨加勁肋深度的增加而增大.但是隨著加勁肋深度的增加，彎矩—撓度曲線的非線性不斷減小.

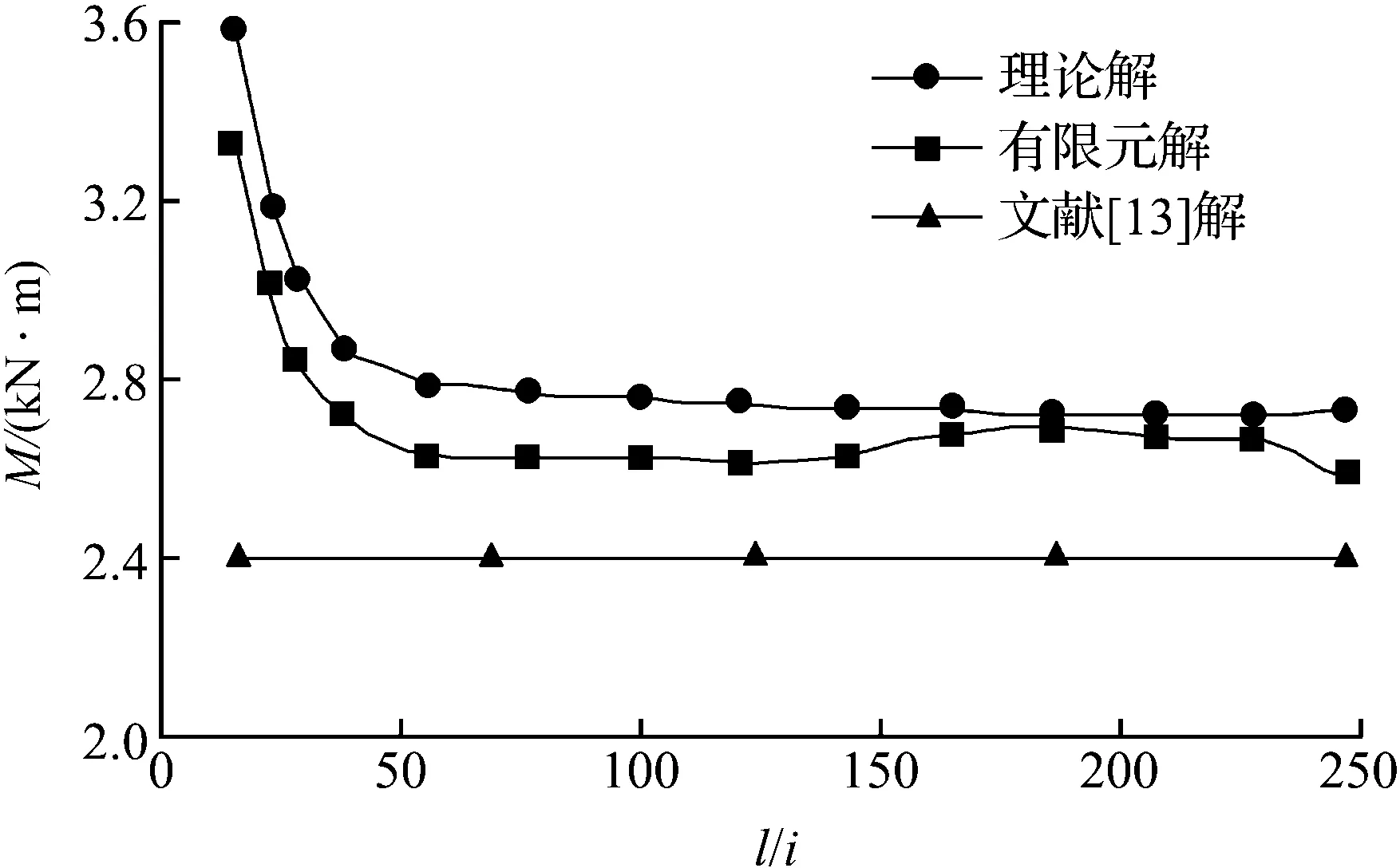
圖5 臨界彎矩—長細比Fig.5 Limit moment versus slenderness ratio

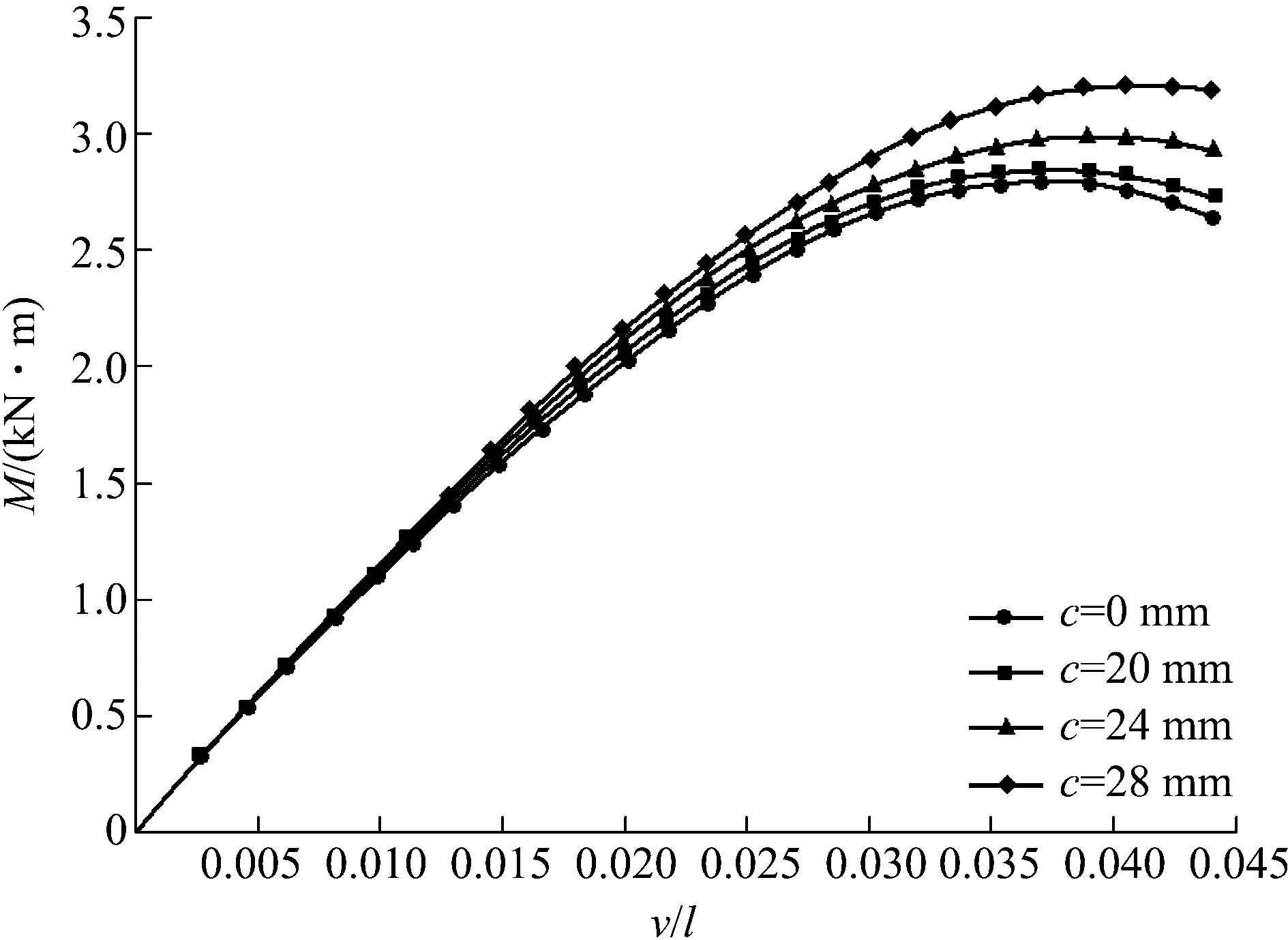
圖6 隨加勁肋深度增加槽鋼梁彎矩—撓度曲線的變化Fig.6 Moment-displacement curves for beams with different stiffener depths

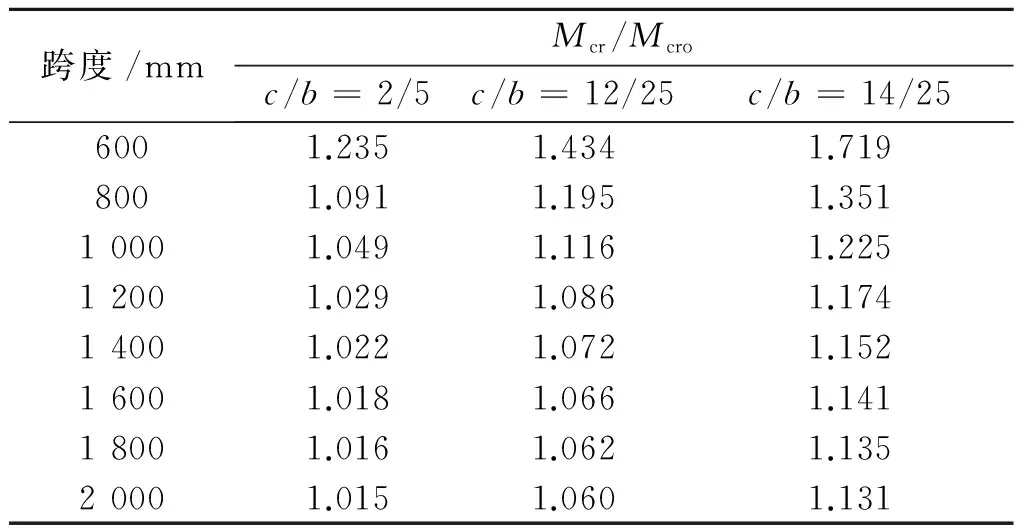
考察跨度增加對加勁肋深度不同的槽鋼梁臨界彎矩的影響，利用式(19)進行計算，所得結果如表1所示.

表1 不同跨度下槽鋼梁加肋效應對臨界彎矩的影響1)(槽鋼截面尺寸h=140 mm,b=50 mm)

Table 1 Effect of stiffener depth on limit moment (i.e. maximum moment) in beams of different beam lengths (h=140 mm,b=50 mm)

跨度/mmMcr/Mcroc/b=2/5c/b=12/25c/b=14/256001.2351.4341.7198001.0911.1951.35110001.0491.1161.22512001.0291.0861.17414001.0221.0721.15216001.0181.0661.14118001.0161.0621.13520001.0151.0601.131

注：1)Mcr為帶肋槽鋼梁臨界彎矩的理論解；Mcro為無肋槽鋼梁臨界彎矩的理論解.

表1表示的是對于截面尺寸為h=140 mm,b=50 mm的槽鋼梁增設3種不同深度的加勁肋，并考察其臨界彎矩隨跨度增加的變化.分析表1可知：隨著跨度的增加，帶肋槽鋼梁的臨界彎矩不斷減小并且趨于其無限長的情況.這是由于隨著跨度的增加，其邊界效應的不斷減弱.同時，還可以注意到加勁肋的深度越深其臨界彎矩值因跨度增加而下降的速率也不斷增加.

4 不帶肋槽鋼非線性彎曲響應的動力分析

眾所周知：雖然結構的臨界動力荷載通常小于相應的臨界靜力荷載，但是當結構受到瞬間荷載作用時的動力失穩(wěn)特征與靜力失穩(wěn)特征類似.通過在靜力分析中運用相似運動假設，就可以通過能量法確定其相應的動力失穩(wěn)荷載.槽鋼梁腹板受到瞬間施加的均布荷載作用而發(fā)生繞弱軸的彎曲.其運動方程可以能量守恒的形式表示為

(22)

式中：T為槽鋼梁的總動能；Π為總勢能，由于定義初始狀態(tài)時(A=wmax=0)總勢能為0，所以式(22)的右端為0.

對一個給定的均布荷載q，式(22)定義了A和wmax對于時間的響應.為了確定臨界動力均布荷載值，假設當槽鋼梁的縱向彎曲響應值(即縱向撓度)達到極值時，截面的扁化響應也同時達到其極值.根據(jù)這個假設，由于當A和wmax達到極值時，dA/dt=0,和dwmax/dt=0，所以在式(22)中，A和wmax振幅的最大值可以通過dA/dt=0,和dwmax/dt=0確定，可以表示為

Π(A,wmax,M)=0

(23)

將式(5，13，14)代入(23)可得

(24)

對式(24)關于A和wmax進行偏導，可得

(25)

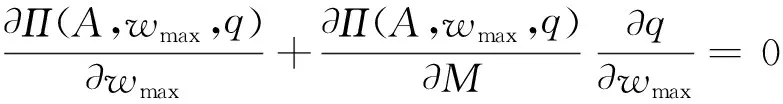
(26)

注意到，動態(tài)失穩(wěn)發(fā)生在，?q/?A=?q/?wmax

=0時，因此，式(25，26)可以簡化式(16，17).這意味著，動態(tài)失穩(wěn)發(fā)生在靜態(tài)平衡能量為0時.因此，動態(tài)失穩(wěn)時的臨界均布荷載qcr，常數(shù)A和腹板扁化量wmax可以通過求解式(16，17，24)，計算結果為

(27)

(28)

(29)

通過與受靜力均布荷載作用槽鋼的計算結果進行對比，可以發(fā)現(xiàn)利用Simitses的方法得到的簡支槽鋼梁繞弱軸的彎曲的臨界動力均布荷載值約為靜力分析時的71%，而其截面的最大扁化變形量wmax約為靜力分析的兩倍，梁的最大撓度約為靜力分析時的1.43倍.

5 結 論

利用改進Brazier的方法求解的薄壁槽鋼非線性彎曲響應曲線與有限元非線性分析的結果比較吻合，盡管理論曲線預測的跨中最大撓度比有限元結果略大，但是理論曲線預測的臨界彎矩與有限元非線性分析得到的臨界彎矩十分吻合(誤差在5%內(nèi)).受均布荷載作用的薄壁槽鋼，隨著跨度的增加，其最大彎矩緩慢下降，但是其最大撓度卻迅速增大(即臨界撓度).并且隨著跨度的增加，其彎曲響應曲線的非線性也逐漸增大.在非線性分析中，對于受均布荷載作用繞弱軸彎曲的槽鋼，當腹板中部增設加勁肋時，其臨界彎矩和臨界撓度都隨加勁肋深度的增加而增大.但是隨著加勁肋深度的增加，彎曲響應曲線的非線性不斷減小.此外，利用Simitses的方法得到的簡支槽鋼梁繞弱軸的彎曲的臨界動力均布荷載值約為靜力分析時的71%，而其扁化變形約為靜力分析的兩倍，梁的最大撓度約為靜力分析時的1.43倍.

[1] MAGNUCKI K, PACZOS P, KASPRZAK J. Elastic buckling of cold-formed thin-walled channel beams with drop flanges[J]. Journal of structural engineering，2014，136(7)：886-896.

[2] LUO H G, GUO Y J, MA S C. Distortional buckling of thin-walled inclined lipped channel beams bending about the minor axis[J]. Journal of constructional steel research,2011,67(12)：1884-1889.

[3] SHIFFERAW Y, SCHAFER B W. Inelastic bending capacity in cold-formed steel members[J]. Journal of structural engineering,2012,138：468-480.

[4] ROGAC M, LUCIC D. Cold formed open thin-walled members analysis-purlin calculations[J]. Tehnika,2013,68(1)：23-33.

[6] BEDAIR O. Design expression for web shear buckling of box sections by accounting for flange restraints[J]. Journal of constructional steel research,2015,110：163-169.

[7] 褚云朋，姚勇，楊亞龍，等.冷彎薄壁方鋼管長柱軸壓性能試驗研究[J].四川建筑科學研究,2014,40(5)：11-15.

[8] 姚行友，郭彥利，劉忠勇，等.冷彎薄壁型鋼軸壓矩形空心管試驗研究及承載力分析[J].建筑技術,2015,46(9)：853-856.

[9] 袁偉斌，徐潔，葉呈敏.純彎下簡支角鋼梁靜態(tài)和動態(tài)不穩(wěn)定性分析[J].浙江工業(yè)大學學報，2013，41(6)：678-681.

[10] 郎婷，趙滇生.蜂窩鋼梁的強度和剛度研究[J].浙江工業(yè)大學學報，2005，33(5)：538-543.

[11] 王森軍，鄭懿，楊俊杰，等.蜂窩梁的撓度影響因素分析[J].浙江工業(yè)大學學報，2007，22(8)：695-698.

[12] 袁偉斌，詹偉，陳昌意.純彎下蜂窩梁的側(cè)向扭轉(zhuǎn)屈曲分析[J].浙江工業(yè)大學學報，2016，44(1)：72-77.

[13] LI L Y.Nonlinear instability analyses of channel section beams subjected to minor-axis pure bending[J]. International journal of mechanical sciences,2013,73:77-81.

[14] 王海明.冷彎薄壁型鋼受彎構件穩(wěn)定性能研究[D].哈爾濱：哈爾濱工業(yè)大學，2009.

(責任編輯：陳石平)

Nonlinear bending of channel-section beams about minor axis under uniformly distributed loading

YUAN Weibin, BAO Zhaoshui, ZHAN Wei
(College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China)

The bending response of simply-supported channel-section beams of finite length about the minor axis is studied using energy methods. The basic assumption used in the paper is that the analysis of the total strain energy of a channel-section beam subjected to uniformly distributed loading is simplified by a two-stage process: the local bending of the web and flange as a plate and the overall bending of the beam with a deformed cross section as a beam. A theoretical solution for the nonlinear bending of channel-section beams with and without longitudinal stiffeners subjected to uniformly distributed loading is derived using the minimum potential energy principle. To validate the derived theoretical solution, a geometric nonlinear finite element analysis is conducted. A good agreement is shown between the present solution and the FEA results. Finally, the dynamic instability of channel-section beams subjected to sudden step uniformly distributed loading is determined using the Simitses method. The effect of the beam length on the nonlinear bending response and critical bending moment of channel-section beams is discussed.

channel-section beam; uniformly distributed loading; deformed deformation; nonlinear instability; finite element method

2016-09-20

袁偉斌(1977—)，男，浙江嵊州人，教授，博士，研究方向為有限元模型理論與應用和鋼與混凝土組合結構，E-mail：yuanwb@zjut.edu.cn.

TU391

A

1006-4303(2017)02-0223-07