深孔臺階爆破近遠區振動特征的試驗研究

韓 亮， 辛崇偉， 梁書鋒， 劉殿書

(1. 華北科技學院 安全工程學院，北京 101601； 2. 北京科技大學 土木與資源工程學院， 北京 100083；3. 中國礦業大學(北京) 力學與建筑工程學院， 北京 100083)

深孔臺階爆破近遠區振動特征的試驗研究

韓 亮1， 辛崇偉2， 梁書鋒3， 劉殿書3

(1. 華北科技學院 安全工程學院，北京 101601； 2. 北京科技大學 土木與資源工程學院， 北京 100083；3. 中國礦業大學(北京) 力學與建筑工程學院， 北京 100083)

為了探索深孔臺階爆破在近區和遠區的振動特征，以現場試驗為基礎，利用回歸分析、隨機分析及小波包分解技術，從爆破振動信號的衰減規律、三分量特征、隨機特征及能量分布等方面對二者進行了對比研究，結果顯示：振速三分量在近區的K、α值均大于遠區，遠區各分量的α值更為接近。振速三分量在遠區的相關系數大于近區，且更接近1，三分量中垂向分量的相關系數最大。近區當比例距離小于5時，徑向振速最大，比例距離大于等于5時，垂向振速最大。遠區的垂向振速最大。無論在近區還是遠區，切向振速一般最小。振速三分量在近區的變異系數大于遠區，徑向振速的變異系數在近區和遠區較為接近。最大段藥量或爆心距增加時，近區及遠區的能量均向低頻帶流動，近區的移動速度更快，同時近區及遠區能量分布的頻帶寬度也將趨于集中，近區的頻帶寬度更寬。

深孔爆破； 近區； 回歸分析； 衰減規律； 隨機變量； 能量分布； 小波包

深孔臺階爆破是礦山、巖土工程生產作業的主要方式，然而爆破帶來的震動效應也極大影響了周邊建筑設施的安全及邊坡穩定。工程中通常采用薩道夫斯基公式估算測點的振動強度，受群孔效應的影響，在爆破地震波作用區域，近區和遠區的預測誤差相差較大。

近區和遠區可通過比例藥量ρ或者比例距離SD來界定，文獻[1]給出的深孔臺階爆破近區范圍ρ在0.24～0.87之間，中遠區ρ在0.08～0.312之間；文獻[2]以振速衰減曲線的斜率為指標，當斜率小于-5時為近區，大于-5為中遠區；文獻[3]建議將比例距離SD等于10作為近區和遠區的分界。上述定義僅考慮了振速衰減規律的異同，并未對爆破振動的其他特征進行分析和比較。此外，爆破近區和遠區屬于特定條件和場地下的相對區域，即便通過統計得到的分布范圍，也很難推廣至其他工程。因此，對于指導工程實踐而言，了解二者在各自范圍內的振動特征比范圍定義更有意義。

目前，國內外關于這方面的研究尚不多見，本文依托深孔臺階爆破現場工程，以大量實測數據為基礎，擬從衰減規律、三分量特征、隨機特征、能量分布等方面，揭示近區和遠區的主要振動特征，研究成果對深孔臺階爆破具有積極的指導意義。

1 爆破振動測試

1.1 測試方案及爆破參數

(1) 測試方案

試驗場地位于北京水泥廠有限責任公司鳳山礦，由于監測目的不同，近區與遠區的爆破振動測試分別位于兩個采場，采場平整，地質條件相差不大。試驗中，以單段最大藥量、最大段群孔爆心距作為參數，計算出各測點的比例距離，以此作為近、遠區的度量。測線沿爆心布置，約4～10個測點，間距10～30 m，所有測點均布置在爆區上平臺后方。近區測試位于測區Ⅰ，單段藥量為1 000～2 000 kg，爆區后方首個測點控制在距爆區40～50 m；遠區測試位于測區Ⅱ，單段藥量為130～500 kg，首個測點位于爆區后方200～500 m，見圖1。

(2) 爆破參數

測區Ⅰ與測區Ⅱ爆破參數基本相同，如表1所示。

(a)

(b)

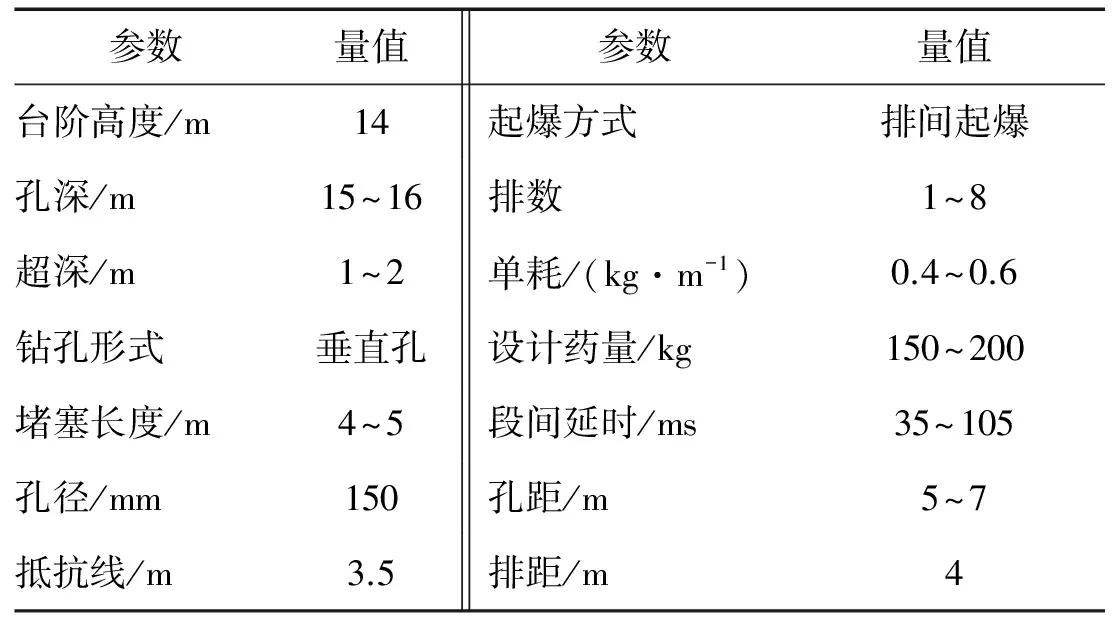
表1 現場爆破參數表

1.2 振動衰減規律

測區Ⅰ與測區Ⅱ分別測得有效數據77組和122組[4]，進行非線性回歸處理，可得爆破近區與遠區水平徑向、水平切向及垂直向振速衰減規律與回歸曲線，見圖2和3。

圖2 近區水平徑向、切向、垂向振速回歸曲線

將回歸計算得到的爆破振動衰減參數K和α值列于表2中。由表2可見，爆破近區中水平徑向、切向和垂向的K、α值均大于遠區。表明爆源爆炸后，震動波經傳播路徑衰減后在近區的剩余爆破能量要大于遠區，同時衰減速度也大于遠區。相對于近區而言，振速三分量的α值在遠區更為接近，表明遠區的振速衰減已趨于穩定，而近區因受多種爆破條件及群孔效應的影響，振速三分量的衰減速度相差較大。

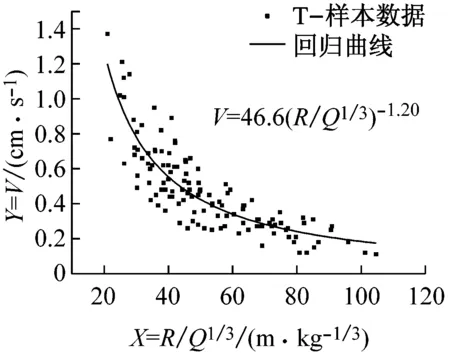
圖3 遠區水平徑向、切向、垂向振速回歸曲線

表2 三方向K、α值比較

將非線性回歸的評價指標相關系數列于表3中。

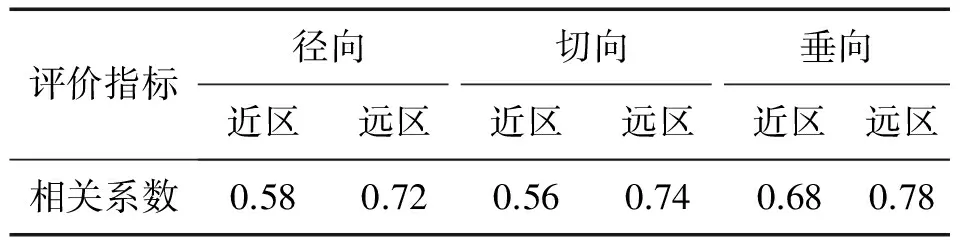
表3 三方向相關系數比較

由表3可見，遠區振速三分量的相關系數大于近區，且更接近1，而無論在近區還是遠區，垂向分量的相關系數均為最大。表明遠區觀測數據在回歸擬合時的規律性要強于近區，同時垂向振速具有更加明晰的方向性，因此，在后續研究中，主要針對垂向分量展開。

2 振速三分量的對比研究

將圖2和3中近區和遠區的觀測值及三分量回歸曲線分別繪于圖4中。由圖4可知，在爆破近區，當比例距離SD<5時，大部分測點的水平徑向振速大于垂向振速；當比例距離SD≥5時，大部分測點的垂向振速大于水平徑向振速。水平切向振速一般最小。在爆破遠區，大部分測點的垂向振速大于水平徑向和切向振速。

根據前人研究[5]，在爆源距離為15倍孔深范圍內，水平徑向振速大于垂向振速。由于試驗現場為深孔臺階爆破，炮孔均為柱狀藥包而非球形藥包。在爆破近區，群孔同時爆破產生的爆破震動波仍有柱狀波陣面的特點，而柱面波在水平徑向的振動速度最大。隨著傳播距離的增大，柱狀波陣面的特點逐漸減弱，群孔爆源才可看做點爆源，因此，爆破遠區垂向振速最大。在水平方向上，切向分量通常小于徑向分量。

(a)

(b)

3 振速幅值的隨機特征

振動觀測中，爆破條件、藥量、爆心距及衰減系數共同決定了爆破振動幅值的大小。在同一塊場地，相同爆破條件下，每一次觀測點距爆心的比例距離一致，得到的爆破地震波幅值均不相同，因此，可以認為在上述條件下觀測的爆破振動幅值具備隨機變量的特征。

假設在爆破近區，同一比例距離處進行了N次爆破振動觀測試驗，得到了N個爆破振動幅值Vi，其中(i=1，2，3,…,N)；同樣在爆破遠區也進行了N次這樣的觀測試驗，得到的N個振動幅值為Ui，(i=1，2，3,…,N)。

根據隨機變量的分布特點，則有

(1)

(2)

上述正態分布的概率密度參數中，μ和σ2均為未知量，因此只能用樣本值Vi和Ui對σ2進行估計。樣本分析時分別選取了近似同一的比例距離(近區為SD=6，遠區為SD=40)下的13組振動觀測數據，見表4。

由概率論知識可知，修正樣本方差S*2是總體方差σ2的無偏估計量。因此可以利用S*2對總體方差σ2進行估計。

表4 相同比例距離下爆破近區和遠區振動觀測數據

根據修正樣本標準差定義，有：

(3)

式中:n為樣本數;xi為樣本數據;x為樣本均值。

由于近區和遠區的振速不在同一數量級，上式得到的修正樣本標準差僅為絕對指標，需對其進一步處理，并用變異系數來表征隨機變量的偏差程度。

變異系數的計算，如下式，

(4)

式中:CV為變異系數;x為樣本均值。

計算結果見表5。由表5可知，近區振速三分量的變異系數均大于遠區，表明近區條件下對振速的影響更為復雜，存在若干未知因素影響著爆破振動的隨機性。同時，三分量中，徑向振速的變異系數在近區和遠區較為接近，表明本試驗中，徑向振速受未知因素的影響最小。

表5 爆破近區與遠區振速變異系數

4 不同爆破條件下能量的分布特征

4.1 振動信號的小波包分析

爆破地震波的產生、傳播以及對建筑物影響的過程，其本質是能量在不同介質中傳遞和轉移的過程。根據先前學者研究，同一爆破場地下，最大段藥量和爆心距[6-7]對能量的分布和衰減影響最大。因此，基于近區和遠區的實測波形，以小波包分析技術為研究手段，分析并比較最大段藥量和爆心距這兩個條件對能量在近區及遠區分布和衰減的影響。

通過試算，選取sym8為最優小波基，采樣頻率為8 000 Hz，小波包分解尺度為9。頻帶寬度依次為：0～7.812 5 Hz、7.812 5～15.625 Hz、15.625～23.437 5 Hz、…、3 992.187 5～4 000 Hz。由于爆破信號在高頻分布較少，這里只對第1～19頻帶的能量分布進行研究，即0～148.437 5 Hz的頻帶范圍。

4.2 最大段藥量對近遠區能量分布的影響

在近區及遠區波形文件中，分別選擇爆心距一定，最大段藥量依次增大的樣本進行小波包分解。樣本情況見表6。得到不同最大段藥量下，近區和遠區各頻帶能量的分布情況，此處僅列舉第1～19頻帶，下同。見圖5。

表6 樣本概況

(a) 近區

通過圖5，可得到如下結論：

(1) 最大段藥量增加時，近區及遠區各測點的低頻帶能量所占比例隨之上升，高頻帶能量所占比例逐漸下降，能量隨最大段藥量的增加向低頻流動，且近區的流動速度更快。

(2) 最大段藥量較小時，近區及遠區能量在1～9頻帶均有分布，且近區的分布寬度較大；隨著最大段藥量的增加，能量分布趨于低頻，近區分布寬度仍大于遠區。由于低頻接近建筑物的自振頻率，因此，最大段藥量的增加將給周邊建筑物安全帶來極大的影響。

4.3 爆心距對近遠區能量分布的影響

在近區及遠區波形文件中，分別選擇最大段藥量一定，爆心距依次增大的樣本進行小波包分解。樣本情況見表7。得到不同爆心距下，近區和遠區各頻帶能量的分布情況，見圖6。

通過圖6，可得到如下結論：

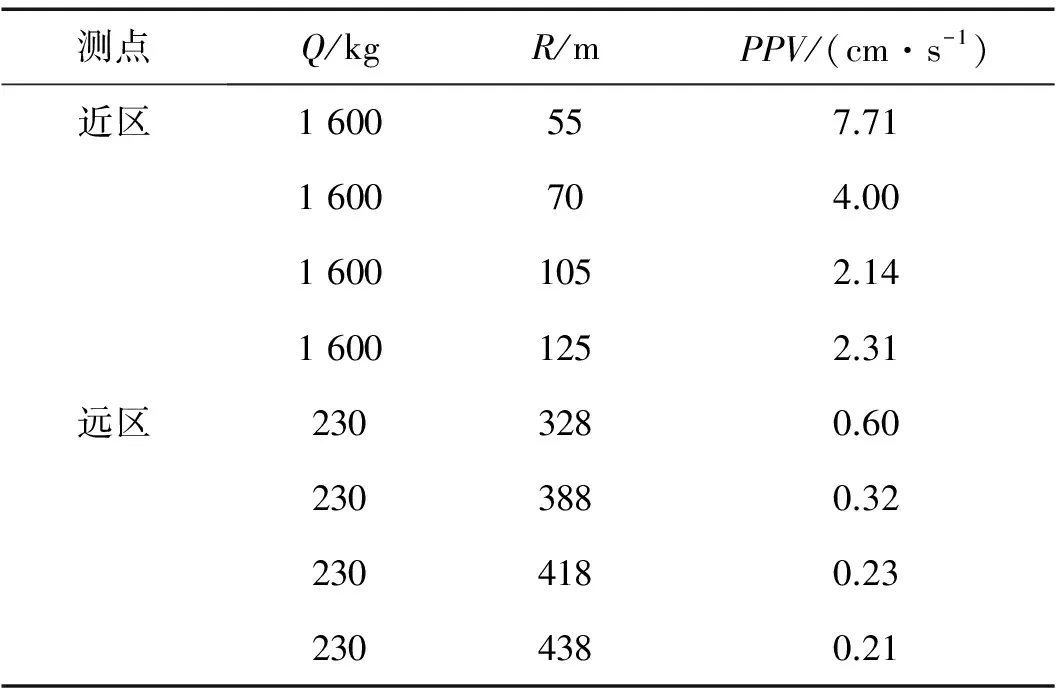
表7 樣本概況

(1) 爆心距增大時，近區及遠區各測點的低頻帶能量所占比例隨之上升，高頻帶能量所占比例逐漸下降，能量隨爆心距的增加向低頻流動，且近區的流動速度更快。

(2) 爆心距較小時，近區及遠區能量在各個頻帶均有分布，分布范圍較寬，且近區的分布寬度較大；隨著爆心距的增加，能量分布趨于低頻，相對而言，遠區能量在低頻帶的集中程度更高。雖然能量隨著爆心距的增加在不斷衰減，但由于低頻能量的集中，將越來越接近建筑物的自然頻率，同樣對周邊建筑物有較大影響。

(a) 近區

(b) 遠區

5 結 論

本文以現場試驗為基礎，利用回歸分析、隨機分析及小波包分解技術，從爆破振動信號的衰減規律、三分量特征、隨機特征及能量分布等方面，對本例中深孔臺階爆破近區和遠區的振動特征進行了對比研究，主要結論如下：

(1) 振速三分量在近區的K、α值均大于遠區，遠區各分量的α值更為接近。振速三分量在遠區的相關系數大于近區，且更接近1，無論在近區還是遠區，垂向分量的相關系數均為最大。

(2) 近區當比例距離小于5時，徑向振速最大，比例距離大于等于5時，垂向振速最大。遠區垂向振速最大。無論在近區還是遠區，切向振速一般最小。

(3) 振速三分量在近區的變異系數均大于遠區，徑向振速的變異系數在近區和遠區較為接近。

(4) 最大段藥量或爆心距增加時，從能量比例上看，近區及遠區的能量都會向低頻帶流動，近區的移動速度要快于遠區；同時近區及遠區能量分布的頻帶寬度也將趨于集中，近區的頻帶寬度也要大于遠區。

[1] 李保珍. 露天深孔爆破地震效應的研究[J]. 長沙礦山研究院季刊, 1989,9(4):84-94.

LI Baozhen. Vibration effect of longhole blasting in open pit mining[J]. Quarterly of CIMR, 1989,9(4):84-94.

[2] 張在晨,林從謀,黃志波,等. 隧道爆破近區振動的預測方法[J]. 爆炸與沖擊, 2014, 34(3): 367-372.

ZHANG Zaichen, LIN Congmou, HUANG Zhibo, et al. Prediction of blasting vibration of area near tunnel blasting source[J]. Explosion and Shock Waves, 2014, 34(3): 367-372.

[3] 楊年華. 爆破振動理論與測控技術[M]. 北京: 中國鐵道出版社, 2014:48.

[4] 韓亮. 深孔臺階爆破近區振動效應的試驗研究[D]. 北京: 中國礦業大學(北京), 2016: 19-25.

[5] 楊年華,張志毅,王平亮,等. 大規模深孔拋擲爆破振動衰減實測與研究[M]. 北京: 冶金工業出版社, 2008: 721-726.

[6] 中國生,敖麗萍,趙奎,等. 基于小波包能量譜爆炸參量對爆破振動信號能量分布的影響[J]. 爆炸與沖擊, 2009, 29(3): 300-305.

ZHONG Guosheng, AO Liping, ZHAO Kui, et al. Influence of explosion parameters on energy distribution of blasting vibration signal based on wavelet packet energy spectrum[J]. Explosion and Shock Waves, 2009, 29(3): 300-305.

[7] 凌同華,李夕兵. 最大段藥量對爆破振動信號頻帶能量分布的影響[J].采礦技術, 2003, 3(4):21-24.

LING Tonghua, LI Xibing. Influence of maximum explosive blasted per delay on frequency bands energy distribution of blasting vibration signals[J]. Mining Technology, 2003, 3(4):21-24.

[8] 盧文波,王進攻. 爆源中遠區的爆破振動場模擬[J].爆破,1996,13(3):8-11.

LU Wenbo, WANG Jingong. A simulation of blasting vibration in middle and far field of explosion source[J]. Blasting, 1996, 13(3): 8-11.

[9] 楊年華,張樂. 爆破振動波疊加數值預測方法[J]. 爆炸與沖擊, 2012, 32(1): 84-90.

YANG Nianhua, ZHANG Le. Blasting vibration waveform prediction method based on superposition principle[J]. Explosion and Shock Waves, 2012, 32(1): 84-90.

[10] 徐全軍,毛志遠,張慶明,等. 深孔微差爆破震動預報淺析[J].爆炸與沖擊, 1998, 18(2): 182-186.

XU Quanjun, MAO Zhiyuan, ZHANG Qingming, et al. The analysis of ground vibration prediction of delay-fired bench blasting[J]. Explosion and Shock Waves, 1998, 18(2): 182-186.

Experimental study on vibration characteristics of deep hole bench blasting in both near and far field

HAN Liang1，XIN Chongwei2，LIANG Shufeng3，LIU Dianshu3

(1. Safety Engineering College, North China Institute of Science and Technology, Beijing 101601, China;2. School of Civil and Resources Engineering, University of Science and Technology Beijing 100083, China;3. School of Mechanics & Civil Engineering, China University of Mining and Technology (Beijing), Beijing 100083, China)

In order to explore the vibration characteristics of deep hole blasting in near and far field, based on field test, this paper used the regression analysis, random analysis and wavelet packet decomposition to carry on a comparative study from the attenuation, three-component characteristic, random characteristic and energy distribution of blasting vibration signals. The results show that the values ofKandαof the three-component of vibration velocity in the near field are both greater than those in the far field. The value ofαof each component in the far field is closer to each other. The correlation coefficient of the three-component vibration velocity in the far field is greater than that in the near field, and closer to 1. The vertical component in the three components is the largest. In the near field, when the scaled distance is less than 5, the radial velocity is the largest, otherwise, the vertical velocity is the largest. In the far field, the vertical velocity is always the largest. Both in the near and far field, the tangential velocity is generally minimal. The coefficient of variation of the three components of vibration velocity in the near field is larger than that in the far field, and the coefficient of variation of the radial velocity are close in the near and far field. When the maximum charge weight per delayed interval or distance is increased, energy in the near and far field gradually move toward the low frequency band, in which it moved faster in near field. At the same time, the frequency band width of energy distribution in the near and far field also tend to focus, and the frequency band width in near field is larger.

deep hole blasting; near field; regression analysis; attenuation law; random variables; energy distribution; wavelet packet

2016-11-10 修改稿收到日期：2016-12-19

韓亮 男，博士，1985年生

劉殿書 男，教授，博士生導師，1960年生

E-mail: lds@cumtb.edu.cn

TD235

A

10.13465/j.cnki.jvs.2017.08.011