一種改進的無導數共軛梯度法

張一夢，賀祖國

（1.北京郵電大學理學院，北京 100876；2.北京郵電大學，北京 100876）

一種改進的無導數共軛梯度法

張一夢1，賀祖國2

（1.北京郵電大學理學院，北京 100876；2.北京郵電大學，北京 100876）

本文基于共軛梯度法的子空間研究，針對無約束優化問題提出了一種改進的無導數共軛梯度法。新算法不僅能有效彌補經典共軛梯度法要求線搜索為精確搜索的局限性，而且可適用于導數信息不易求得甚至完全不可得的問題。實驗結果表明：相比于一次多項式插值法、有限差商共軛梯度法以及有限差商擬牛頓法，新算法的效率有很大的提高。

無約束最優化；無導數優化；子空間；共軛梯度法

0 引言

考慮無約束極小化問題

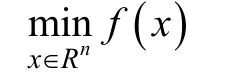
其中f:Rn→R二次連續可微。

目標函數的導數信息（梯度和 Hessian矩陣）在優化過程有著非常重要的作用。例如，對一個目標函數連續可微的無約束優化問題來說，由一階最優性條件確定的穩定點處，其梯度為零。導數信息不僅能提供簡單有效的停止準則，并且能有效的指引對試探點的選取。然而，很多來源于實際應用的優化問題的導數信息不易求得甚至完全無法得到，因此解決這類問題需要用無導數優化方法，也稱為直接方法。

早期的無導數方法例如單純形法，簡單直觀并且易于實現。發展到現在，無導數優化方法有直接搜索法[1-3]，線搜索法[4-6]，隨機性算法，有限差商共軛梯度法和擬牛頓法[7]，基于差值模型逼近的信賴域方法等。

本文基于共軛梯度法的子空間研究[8]，將其運用于多項式插值算法中得到一種改進的無導數共軛梯度法。……