有限元指紋圖像配準*

姚麗莎，程家興

安徽新華學院 信息系統軟件研究所，合肥 230088

有限元指紋圖像配準*

姚麗莎+，程家興

安徽新華學院 信息系統軟件研究所，合肥 230088

針對指紋圖像中形變復雜多樣的特點，對指紋圖像配準算法進行研究，發現目前指紋配準算法存在復雜度高，精度低，速度慢，易受指紋形變等影響的缺陷，引入有限元分析理論，提出了有限元指紋圖像配準算法。該算法將指紋圖像配準中的復雜形變轉換為有限個離散形變單元組成的彈性形變，以分叉點、轉折點、指紋圖像上兩點的連線所穿越的脊線數量等特征作為特征指標，求出采樣指紋與標準指紋的模糊貼近度，并創造性地以此為相似性測度，構造總體剛度方程，進而迭代求解最佳位移，完成指紋圖像配準。實驗表明，該算法位移量的誤差最小，用時為8.894 s，其有效降低了算法復雜度，提高了精度，同時也有效避免了指紋復雜多樣的形變等因素對指紋配準算法精度的影響。

指紋配準；有限元；模糊貼近度；指紋特征點

1 引言

在生物特征識別領域中，指紋識別技術[1]發展迅速。信息技術的飛速發展在為自動指紋識別的應用開辟廣闊市場的同時，也對指紋識別技術提出了新的挑戰。指紋匹配[2]的準確性與效率對指紋識別的優劣有直接影響，它是指紋識別的核心內容。

然而，在實際指紋采樣的工作過程中存在著復雜的形變問題，如采樣手指的角度偏差，指紋粗糙度發生較大變化，采樣手指壓力不同等都會造成指紋圖像的形變。基于細節點模式的指紋匹配算法在匹配前需找到采樣指紋與庫指紋的形變變換的最優解，即指紋配準。為提高指紋識別的準確率，提高指紋匹配的準確性，就要提高指紋配準的準確性。國內外許多研究人員在指紋配準上提出了許多研究成果，如文獻[3]的基于新的細節點柱形編碼的指紋匹配算法，文獻[4]的基于細節點全局置信度的指紋匹配算法等。還有一些研究在圖像配準中應用力學上的有限元模型，Schnabel等人將有限元法應用于求解基于B樣條精配準前的初始變換[5]；Xuan等人利用樣條曲線為有限元模型控制局部形變[6]。但這些算法對配準精度有所限制，大多只能用于粗配準，不能解決指紋圖像的復雜形變問題。

目前指紋配準算法存在復雜度高，精度低，速度慢，易受指紋形變等影響的缺陷，為解決指紋圖像復雜形變問題，本文引入有限元分析理論，提出了一種新的基于有限元分析理論的指紋圖像配準算法。首先將配準圖像進行有限次離散化的劃分，并將指紋圖像配準中的復雜形變轉換為有限個離散形變單元組成的彈性形變，以提高指紋配準算法的精度和速度。為解決現有基本有限元算法對剛體位移不敏感，精度具有局限性的缺陷，求解配準過程中有限元的能量函數時，創造性地以分叉點、轉折點、指紋圖像上兩點的連線所穿越的脊線數量等特征作為特征指標，求出采樣指紋與標準指紋的模糊貼近度。采用采樣指紋與標準指紋的模糊貼近度測度為驅動，構造總體剛度方程，提高圖像配準的精度。該算法可有效削弱因指紋平移、旋轉、手指壓力不均等因素造成的對指紋配準準確度的影響。

2 有限元配準

有限元理論是“先化整為零，再集零為整”。最終解看成是由有限個有限單元的近似解組成，然后根據有限個單元近似解推導求解總的最終解。這樣復雜問題就轉換為若干個簡單問題，能適應各種復雜問題的求解。

指紋圖像具有復雜形變問題[7]，配準過程可以歸結為某個量的極值問題[8]。指紋圖像的有限元配準就是將復雜的形變體轉化為較為簡單的離散的有限個形變單元，以此為基本單位，依據圖像的能量函數，對整個圖像的形變進行計算。

有限元法求解復雜問題的基本思路可概括為3個步驟，即對彈性體進行結構離散化、單元分析和整體分析，如圖1所示。

對兩幅待配準的指紋圖像A、B在配準中進行單元劃分，選取像素點的位移u為待定位移函數，在所有可能滿足位移邊界條件的位移中，搜索可以滿足平衡條件的位移，使總勢能E成為極小值，此位移即為平衡條件下近似解[9]。以位移u為例，該能量泛函可以用泰勒展開式表達：

Fig.1 Analytical procedure using finite element method圖1 有限元法分析步驟

其中，ε為應變；σ為應力；?為用于能量計算的梯度算子；2(I1-I2)?I1u表示彈性形變；(I1-I2)2表示剛體的位移。高階導數不一定滿足一致連續性，因此通常只考慮彈性形變項而省略位移項，這樣便將圖像配準問題轉化為求解位移解u的有限元問題。

3 模糊貼近度

指紋紋線的端點（末稍點）和分叉點被視為指紋的主要特征點[10-11]，如圖2所示。指紋圖像特征點的絕對位置可能會隨著指紋圖像的平移、旋轉或局部形變發生很大變化，然而兩個特征點的連線所穿越的脊線數目及特征點構成的多邊形的邊和角則不會發生較大改變，這是衡量指紋圖像匹配程度的重要特征指標[12-13]。

Fig.2 Endpoint and cross point of fingerprint image圖2 指紋圖像的端點和叉點圖

指紋中心點也是指紋圖像的主要特征點，指紋線在此點處匯聚，形成收斂，如圖3所示。以指紋中心點為參考點，可確定各特征點的位置，具體方法是：

Fig.3 Information map of fingerprint feature points圖3 指紋特征點信息圖

（1）若最內層隆起線是一條直線，則確定隆起線的上端點為中心點；

（2）若最內層隆起線的上凸部分出現分叉，則確定分叉為中心點；

（3）若隆起線存在多條，則確定最左邊的隆起線的上端點為中心點。

在確定指紋中心點后，以與中心點距離大于D (0＜D≤10)且最近的4個點（M,N,P,Q）為其特征點，連接這4個點構成四邊形MNPQ，如圖4所示。

Fig.4 Apolygon consisting of fingerprint feature points圖4 指紋特征點多邊形

指紋特征點組成的四邊形MNPQ中4個點間的距離可分別由式（2）～式（6）求得：

四邊形MNPQ中的兩個夾角a與b的值由式（7）、式（8）求得：

衡量指紋匹配程度的重要指標為兩點連線所穿越的脊線數量。因為指紋圖像上兩點連線所穿越的脊線數量不會隨著指紋圖像發生平移、旋轉、縮放等形變而發生變化。依據參考文獻[14]所給出的方法計算MN和NP連線所穿越的脊線數量Imn和Inp。

設論域U={X1,X2,…,Xn}[15]有n個模糊子集 ω1, ω2,…,ωn，構成了標準指紋庫。B為采樣指紋，σ(ωi,B)表示B與ωi(i=1,2,…,n)的模糊貼近度。若σ(ωm,B)= max{σ(ω1,B),σ(ω2,B),…,σ(ωn,B)}，則B最貼近 ωm，B應歸于ωm。用模糊貼近度σ(ω,B)作為指紋圖像配準的測度函數，其應滿足如下條件：

（1）σ(ω,ω)=1；

（2）σ(ω,B)=σ(B,ω)；

（3）σ(?,U)=0,其中?為空集；

（4）由ω?B?C可得σ(ω,C)≤σ(ω,B)∧σ(B,C)，其中C為模糊集[16]。

由此推導出模糊貼近度公式為：

本文利用特征點構成的多邊形的邊、角及兩個點的連線所穿越的脊線數目為特征指標求兩幅圖像的模糊貼近度，以此為測度函數，進而不斷迭代，從而求解最佳位移解。

4 有限元指紋圖像配準算法

4.1 總體剛度方程構造

式（1）通過泰勒公式展開后，由于高階導數不一定滿足一致連續，通常省略位移項，而只考慮彈性形變項，但是省略剛體位移項，常會帶來在配準過程中，對較大位移和旋轉等剛性變換不夠敏感的問題，進而影響指紋圖像配準的準確性。為此本文將模糊貼近度用于有限元理論中對指紋圖像進行配準。

總體剛度方程的構造是整個配準過程的關鍵。彈性形變后，內部各點發生位移。在有限元分析理論中，將整體離散化，用一個相對簡單的函數來描述單元內每個點的位移，稱為位移函數。因為多項式便于計算而且能逼近任何復雜函數，所以一般用系數多項式來表示二維平面問題的位移函數。如圖5所示，以三角單元位移Δ為例，其3個節點編碼依逆時針方向進行，依次為i、j、k。單元的每個節點在平面問題中具有兩個自由度。

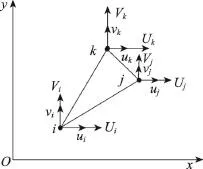
Fig.5 Three nodes of triangular element圖5 三角單元3節點

經過推導，位移函數表達式為：

其中，Ni表示插值函數，反映單元的位移變化形態，故稱形函數。

下標i、j、k輪換，表示三角形單元的3個節點，其中系數ai、bi、ci的取值用克萊姆法則求得：

S表示三角形的面積，其計算公式為：

Δ=Nue為位移函數矩陣，其中ue是單元節點位移列陣，如式（14）所示：

單元節點位移與單元體內應變及應力的關系可以根據廣義胡克定律、彈性體幾何方程式ε=LΔ（L為變換矩陣）、式（10）得到：

式（15）中，B是幾何矩陣，其大小為B=LN；ε表示應變矩陣；ζ表示應力矩陣；D表示彈性矩陣。有如下關系：

式（16）中，E為楊氏模量（Young’s modulus），其大小表示固體材料抗形變的能量；v為泊松比；ζx、ζy、τxy為應力矩陣ζ的應力分量；εx、εy、γxy為應變矩陣ε的應變分量。

將上述單元體各分量組合：

對于二維有限元，等效能量梯度與每個等效節點力 f(fix,fiy)成正比，故有：

其中，U是總體位移陣列；K是總體剛度矩陣；R是全部外力的等效節點力陣列；α是正系數；?m表示相似性測度的梯度。本文將模糊貼近度作為測度，即這里m為模糊貼近度，因此有：

其中，σ(A,B)為標準圖像A與采樣圖像B單元體模糊貼近度。這里以單元體內局部中心點來確定特征點，以特征點構成的多邊形的邊、角及兩個點的連線所穿越的脊線數目為特征指標求標準圖像A與采樣圖像B的單元體模糊貼近度。

該算法以有限元模擬形變模型，既考慮了圖像的物理形變，又融入了圖像的模糊貼近度為度量。

各個單元體勢能的總和為結構體總的勢能，在離散化的情況下有：

4.2 算法步驟

本文利用有限元分析理論將指紋配準問題的復雜形變轉換為有限個離散形變單元組成的彈性形變問題，使用模糊貼近度為相似性測度，構造總體剛度方程，進而不斷迭代求解最佳位移。

在確立有限元材質并設置屬性參數的基礎上，首先，對采樣指紋圖像進行插值，依據當前測度函數求解位移的初始值；然后，以模糊貼近度為測度不斷迭代求解新的位移解，當兩次求得的位移解的差值小于某一特定極小值時迭代結束，此時的位移解即為最終值。圖6所示為本文配準算法流程圖。

5 實驗結果與分析

實驗分別采用文獻[3]基于新的細節點柱形編碼的指紋匹配算法、文獻[4]基于細節點全局置信度的指紋匹配算法和本文算法進行比較。

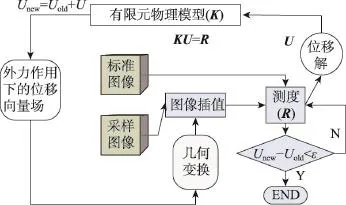
Fig.6 Flow chart of registration algorithm in this paper圖6 本文配準算法流程圖

實驗1選取標準指紋圖像如圖7（a）和采樣指紋圖像如圖7（b）進行指紋圖像配準，3種算法的配準結果分別如圖7（c）、（d）、（e）所示。

在實驗過程中記錄不同迭代次數下位移量x、y以及旋轉角度θ的變化情況，如圖8（a）、（b）、（c）所示。這里位移量x、y以及旋轉角度θ的標準值為100、100、58。實驗用標準指紋圖像與配準后的指紋圖像的均方根R來作為評價參數，比較3種算法在不同迭代次數下的變化情況，如圖8（d）所示。

式中，n表示圖像大小；Tr(x)表示配準結果；Tq(x)表示標準圖像。R越小表示兩幅圖像的差異越小。

實驗1表明本文算法與文獻[3]、[4]算法的比較結果：從圖8（a）、（b）、（c）可以看出，在不同迭代次數下，本文算法對形變更為敏感，均更接近于實際位移量，配準效果更優；從圖8（d）可以看出，誤配率明顯降低，在精度上有顯著提升。

實驗2選取標準指紋圖像如圖9（a）和采樣質量較差存在復雜形變的指紋圖像如圖9（b）進行指紋圖像配準，3種配準算法的配準結果分別如圖9（c）、（d）、（e）所示。

在實驗過程中記錄不同迭代次數下位移量x、y以及旋轉角度θ的變化情況，如圖10（a）、（b）、（c）所示。這里位移量x、y以及旋轉角度θ的標準值為10、10、14。3種算法的均方根在不同迭代次數下的變化情況如圖10（d）所示。

實驗2采用了質量較差存在復雜形變的采樣圖像，結果表明本文算法與文獻[3]、[4]算法相比，亦取得良好的實驗結果，有效避免了指紋復雜多樣的形變等因素對指紋配準算法精度的影響。

實驗3為了進一步驗證算法的有效性，實驗選取10對不同的指紋圖像分別用3種算法進行圖像配準。以Δxˉ、Δyˉ、Δθˉ、Tˉ即水平位移量、垂直位移量、旋轉偏移量誤差的平均值及算法平均執行時間為依據來比較以上3種配準算法，結果如表1所示。

Table 1 Parameter results of different registration algorithms表1 不同配準算法的參數結果

Fig.7 Registration results of experiment 1圖7 實驗1配準結果圖

Fig.8 Parametric variation of experiment 1圖8 實驗1參數變化情況圖

Fig.9 Registration results of experiment 2圖9 實驗2配準結果圖

本文算法將指紋圖像配準中的復雜形變轉換為有限個離散形變單元組成的彈性形變，提高指紋配準算法的精度和速度。為解決現有基本有限元算法對剛體位移不敏感，精度具有局限性的缺陷，以分叉點、轉折點、指紋圖像上兩點的連線所穿越的脊線數量等特征作為特征指標，求解配準過程中有限元的能量函數，并采用采樣指紋與標準指紋的模糊貼近度測度為驅動，構造總體剛度方程，提高圖像配準的精度。本文算法可有效削弱因指紋平移、旋轉、手指壓力不均等因素造成對指紋配準準確度的影響。從表1可以看出，從水平位移量、垂直位移量、旋轉偏移量誤差的平均值上可見本文算法優于其他兩種算法。從算法平均執行時間可見，本文算法的效率優于其他兩種算法。

Fig.10 Parametric variation of experiment 2圖10 實驗2參數變化情況圖

6 結束語

本文采用有限元和模糊貼近度對指紋圖像進行配準。有限元模型能夠逼近指紋圖像總的精確形變，在有限單元內創造性地采用模糊貼近度為能量函數，對剛體位移變化更敏感。實驗表明，本文算法水平位移量、垂直位移量、旋轉偏移量誤差的平均值分別為3.084 721 mm、3.897 214 mm、2.651 432°，較其他兩種算法誤差最小；算法平均執行時間為8.894 s，用時最少。本文算法提高了精度，降低了復雜度，并且實驗2表明本文算法有效避免了指紋圖像復雜形變問題對配準精度的影響。

[1]Zhang Bo.Research on incomplete fingerprint recognition based on data mining and information[D].Beijing:Beijing University of Posts and Telecommunications,2012.

[2]Li Ke.The research of fingerprint recognition system based on sparse matrix[D].Wuhan:Wuhan University of Science and Technology,2012.

[3]Cappelli R,Ferrara M,Maltoni D.Minutia cylinder-code:a new representation and matching techinque for fingerprint recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(12):2128-2141.

[4]Fu Xiang,Feng Jufu.An fingerprint matching algorithm based on minutia global confidence[J].Pattern Recognition andArtificial Intelligence,2014,27(9):835-840.

[5]Schnabel J A,Tanner C,Castellano-Smiih A D,et al.Validation of non-rigid image registration using finite elementmethods application to breast MR images[J].IEEE Transaction on Medical Imaging,2003,22(2):238-247.

[6]Xuan Jianhua,Wang Yue,Freedman M T,et al.Nonrigid medical image registration by finite element deformable sheet-curve models[J].International Journal of Biomedical Imaging,2006,13(4):1-9.

[7]Zhang Jie.Researches on the key technologies in incomplete fingerprint recognition[D].Beijing:Beijing University of Posts and Telecommunications,2013.

[8]Zeng Chao,Li Na,Wang Wei,et al.Registration of medical images using group search optimizer combined with Powell’s method[J].Journal of Yunnan University:Natural Sciences Edition,2013,35(5):603-609.

[9]Krol A,Unlu M Z,Magri A,et al.Iterative finite element deformable model for non-rigid coregistration of multimodal breast images[C]//Proceedings of the 3rd IEEE Intemational Symposium on Biomedical Imaging:Nano to Macro,Arlington,Apr 6-9,2006.Piscataway,USA:IEEE,2006:852-855.

[10]Popuri K,Cobzas D,J?gersand M.Fast FEM-based non-rigid registration[C]//Proceedings of the 2010 Canadian Conference on Computer and Robot Vision,Ottawa,May 31-Jun 2,2010.Washington:IEEE Computer Society,2010:378-385.

[11]Zhang Yuanyuan.Researches on fingerprint identification related algorithms[D].Beijing:Beijing University of Posts and Telecommunications,2012.

[12]Chen Xiaoguang,Feng Jufu.A novel algorithm for distorted fingerprint matching using stable regions[J].Journal of Image and Graphics,2010,15(8):1220-1229.

[13]Chen Hongtao.A study of fingerprint recognition and encryption based on entropy analysis[D].Xi’an:Xidian University,2012.

[14]Chai Haiyan,Tian Dongping,Fan Jiulun,et al.Fingerprint minutia matching algorithm based on similar triangle theory [J].Communications Technology,2009,42(10):57-59.

[15]Yuan Dongfeng,Du Heng,Qin Xiaotie.Fingerprint matching algorithm based on local triangular feature point model[J]. Journal of Chongqing Normal University:Natural Science, 2013,30(2):69-73.

[16]Xie Jijian,Liu Chengping.Fuzzy mathematics method and its application[M].Wuhan:Huazhong University of Science and Technology Press,2008:61-122.

附中文參考文獻：

[1]張博.基于數據挖掘和融合理論的殘缺指紋識別應用研究用[D].北京:北京郵電大學,2012.

[2]李珂.基于稀疏矩陣的指紋識別系統研究[D].武漢:武漢科技大學,2012.

[4]付翔,封舉富.一種基于細節點全局置信度的指紋匹配算法[J].模式識別與人工智能,2014,27(9):835-840.

[7]張潔.殘缺指紋識別中若干關鍵技術的研究[D].北京:北京郵電大學,2013.

[8]曾超,李娜,王維,等.群搜索算法與Powell法結合的醫學圖像配準[J].云南大學學報:自然科學版,2013,35(5): 603-609.

[11]張圓圓.指紋識別技術相關算法的研究[D].北京:北京郵電大學,2012.

[12]陳小光,封舉富.基于穩定區域的形變指紋匹配算法[J].中國圖象圖形學報,2010,15(8):1220-1229.

[13]陳宏濤.基于熵分析的指紋識別與加密算法應用研究[D].西安:西安電子科技大學,2012.

[14]柴海燕,田東平,范九倫,等.基于相似三角形原理的指紋匹配算法[J].通信技術,2009,42(10):57-59.

[15]袁東鋒,杜恒,秦小鐵.基于三角形局部特征點模型指紋匹配算法[J].重慶師范大學學報:自然科學版,2013,30 (2):69-73.

[16]謝季堅,劉承平.模糊數學方法及應用[M].武漢:華中科技大學出版社,2008:61-122.

YAO Lisha was born in 1986.She received the M.S.degree from Anhui University in 2011.Now she is a lecturer at Anhui Xinhua University.Her research interests include image processing,pattern recognition and artificial intelligence,etc.

姚麗莎（1986—），女，安徽合肥人，2011年于安徽大學獲得碩士學位，現為安徽新華學院講師，主要研究領域為圖像處理，模式識別，人工智能等。主持兩項安徽省高校自然科學重點研究項目。

CHENG Jiaxing was born in 1946.He received the Ph.D.degree from University of South Australia in 1997.Now he is a professor and Ph.D.supervisor at Anhui Xinhua University.His research interests include intelligent computing, pattern recognition and bio-informatics,etc.

程家興（1946—），男，安徽合肥人，1997年于澳大利亞南澳大學獲得博士學位，現為安徽新華學院教授、博士生導師，主要研究領域為智能計算，模式識別，生物信息學等。發表學術論文100余篇，主持2項國家自然科學基金項目，1項教育部優秀留學回國人員基金項目。

Fingerprint Registration Based on Finite Element*

YAO Lisha+,CHENG Jiaxing
Institute of Information Systems Software,Anhui Xinhua University,Hefei 230088,China
+Corresponding author:E-mail:jsjyaolisha@163.com

Fingerprint registration algorithm is studied for the complexity and variety of fingerprint deformation.Because the existing fingerprint registration algorithms have the defects of high complexity,low precision,slow speed and easy to be affected by fingerprint deformation,this paper introduces finite element analysis theory,and proposes a fingerprint registration algorithm based on finite element.In this algorithm,discrete finite element is used as basic unit to simulate the deformation of whole elastomer for complex deformation in fingerprint images.It takes the turning point,bifurcation point,the number of ridge lines between two points in fingerprint images and so on as the features. The fuzzy similarity is creatively proposed as metric for solving the overall stiffness equation to complete fingerprint registration.The experimental results show that the error of displacement of the proposed algorithm is the smallest and the time is 8.894 seconds,it lowers the complexity,and also improves the precision.At the same time,it can avoid the influence of the complexity and variety of fingerprint deformation on the accuracy of the fingerprint registration algorithm.

fingerprint registration;finite element;fuzzy similarity;fingerprint feature points

10.3778/j.issn.1673-9418.1602033

A

TP391.41

*The Natural Science Research Project of Anhui Colleges and Universities under Grant No.KJ2015A309(安徽省高校自然科學重點研究項目).

Received 2016-02,Accepted 2016-06.

CNKI網絡優先出版:2016-06-02,http://www.cnki.net/kcms/detail/11.5602.TP.20160602.1144.004.html

YAO Lisha,CHENG Jiaxing.Fingerprint registration based on finite element.Journal of Frontiers of Computer Science and Technology,2017,11(4)：643-651.