滑塌式危巖破壞斷裂力學分析

陳斯祺

摘 要：危巖是一種全球性高頻率的地質災害，其中滑塌式危巖破壞是危巖主要的破壞類型之一。該文針對滑塌式巖石破壞類型，通過考慮自重、裂隙水壓力和地震力3種組合荷載構建滑塌式危巖力學模型，采用斷裂力學的方法推導其Ⅰ-Ⅱ型復合應力強度因子。根據最大周向應力理論，使用三角形萬能公式計算變形得出其理論斷裂角。

關鍵詞：斷裂力學 Ⅰ-Ⅱ型復合應力強度因子 斷裂角 滑塌式危巖

中圖分類號：TU45 文獻標識碼：A 文章編號：1674-098X（2017）01（c）-0009-0

巖石是由一種或多種礦物在地質作用下天然產生的復雜結構體。大多巖體工程中的巖石屬于壓剪狀態，其巖石裂縫的應力場應為壓剪應力場。滑塌式危巖破壞的本質是壓剪破壞，因此對于滑塌式危巖破壞的研究具有必要性和迫切性。眾多國內外學者都致力于對巖石破壞的機理進行了相應的研究。Nara Y等[1]以處于亞臨界裂紋擴展狀態的花崗巖為研究對象，他發現裂隙水將加速花崗巖裂紋擴展的速度并影響花崗巖的結構強度。Zygouri V等[2]對Skolis山和Acrocorinthos的巖石進行了研究，研究表明淺層地震會引起大范圍的巖石崩塌。Chen H K等[3]提出了處于激勵效應下的不穩定巖石的破壞準則并建立了對其安全性的評估方法。Johari A等[4]采用聯合分布隨機變量的方法對處于臨界狀態的巖石的穩定性進行了可靠的評估。Li Y等[5]使用FLAC3D軟件模擬了節理裂隙水壓力作用下巖體的裂隙發育，結果表明裂隙水對節理巖體的強度和穩定性有明顯的降低作用。Liang L等[6]在龍馬溪地區對頁巖進行取樣，研究表明水性液體對頁巖形成的裂紋擴展具有顯著的正向影響。迄今為止，學者多以試驗和數值分析的方法對巖石裂縫進行研究，對于巖石裂縫的理論分析略有欠缺。該文采用斷裂力學的方法對滑塌式危巖進行理論推導，其結果對于防災減災和工程安全評估等方面具有一定的理論意義和經濟價值。

1 應力分量的坐標變換

如圖1所示，建立滑塌式危巖模型。其中為危巖體重心，為主控結構面的孔隙水壓力，為單位長度水平地震力，為單位長度豎向地震力，為單位長度的巖體重力。

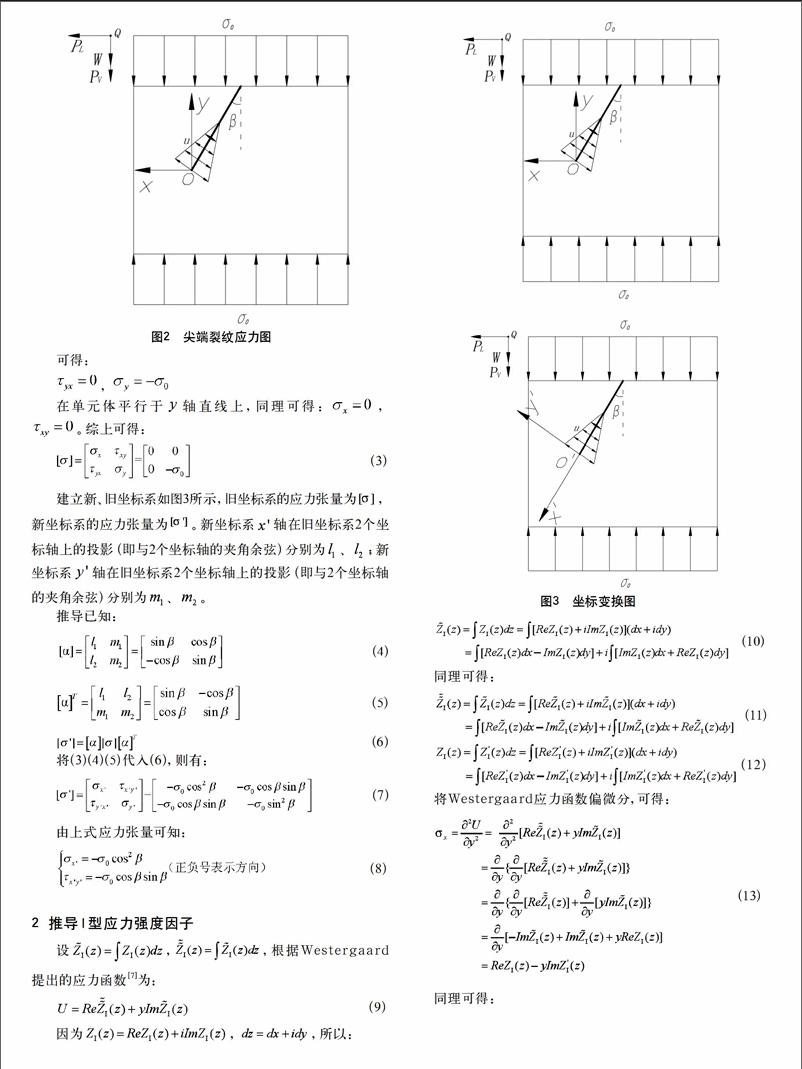
在圖1中的裂紋尖端選取單元體，在巖石自身重力作用下形成壓剪應力（如圖2）。

在單元體平行于軸的直線上，設其外法線與坐標軸的夾角分別為、，則有：

，，，

將已知參數帶入邊界條件方程：

（1）

（2）

可得：

，

在單元體平行于軸直線上，同理可得：，。綜上可得：

（3）

建立新、舊坐標系如圖3所示，舊坐標系的應力張量為，新坐標系的應力張量為。新坐標系軸在舊坐標系2個坐標軸上的投影（即與2個坐標軸的夾角余弦）分別為、；新坐標系軸在舊坐標系2個坐標軸上的投影（即與2個坐標軸的夾角余弦）分別為、。

推導已知：

（4）

（5）

（6）

將（3）（4）（5）代入（6），則有：

（7）

由上式應力張量可知：

（8）

2 推導Ⅰ型應力強度因子

設，，根據Westergaard提出的應力函數[7]為：

（9）

因為，，所以：

（10）

同理可得：

（11）

（12）

將Westergaard應力函數偏微分，可得：

（13）

同理可得：

（14）

（15）

將（13）（14）（15）整理，可知：

（16）

如圖4所示，在無限體內有一個長為的中心貫穿裂紋，在其無窮遠處受雙向均勻應力作用。其邊界條件為：當，a時，>；當，。

由（16）式可知，當，時，；當，時，。可將其應力函數假設為：

由于其裂紋關于軸對稱，因此假設其應力函數為：

由于上述應力函數是在，的特殊情況下推導的。對于大多數情況下，因此可將上式中用代替，則有：

（17）

將原坐標點移新坐標點，設新坐標系中任意一點的復數坐標為，則兩坐標系的換算關系如下：

（18）

即：

（19）

將（19）式帶入（17）式：

（20）

當時，令

（21）

由于當→0時，為一常數。因此，可令常數為：

（22）

聯解（20）（21）（22），可得：

（23）

3 推導Ⅱ型應力強度因子

設，，根據Westergaard提出的應力函數[7]為

（24）

因為，，所以：

（25）

同理可得：

（26）

（27）

將Westergaard應力函數偏微分，可得：

（28）

同理可得：

（29）

（30）

將（28）（29）（30）整理，可知：

（31）

如圖5所示，在無限體內有一個長為的中心貫穿裂紋，在其無窮遠處受雙向均勻剪應力作用。其邊界條件為：當，a時，>；當，。

由（16）式可知，當，時，；當，時，可將其應力函數假設為：

由于其裂紋關于軸對稱，因此假設其應力函數假設為：

由于上述應力函數是在，的特殊情況下推導的。對于大多數情況下，因此可將上式中的用代替，則有：

（32）

將原坐標點移新坐標點，設新坐標系中任意一點的復數坐標為，則兩坐標系的換算關系如下：

（33）

即：

（34）

將（34）式帶入（32）式：

（35）

當→0時，令

（36）

由于當→0時，為一常數。因此，可令常數為：

（37）

聯解（35）（36）（37），可得：

（38）

4 推導不穩定巖石的Ⅰ-Ⅱ復合應力強度因子和斷裂角

令Ⅰ-Ⅱ復合型裂紋的裂尖應力強度因子為：

（39）

聯解（23）（38）（39）可得如下關系：

（40）

由于水平地震力和豎向地震力不能同時考慮，因此可分別在其前面添加一個系數和，構建如下函數：

（41）

設危巖其重心點的坐標為，為主控結構面的孔隙水壓力的最大值，為軸方向的分量總和，為軸方向的分量總和，則有：

（42）

（43）

設為常數，根據Ⅰ型裂紋的Westergaard應力函數，可得：

（44）

設為常數，根據Ⅱ型裂紋的Westergaard應力函數，可得：

（45）

聯解（8）（28）（32）（33）可得：

（46）

根據最大周向應力理論（準則）[8]，可以求其解斷裂角。

（47）

令，帶入（47），則有：

（48）

根據一元二次方程可解得：

當時，其斷裂角大于180°，裂紋將向反方向擴展，顯然與實際情況不符，應當舍去。

因此，可得理論斷裂角θ0為：

（49）

5 算例分析

重慶市萬州危巖w15屬滑塌式危巖，其高度為9.5 m，長度為4 m，厚度為20.5 m，裂縫長度為18.5 m，將其荷載擬定為重慶市地方規范手冊中的工況三（自重+裂隙水壓力+地震力）。通過該文推導的Ⅰ-Ⅱ復合型裂紋的應力強度因子公式可得其KⅠ應力強度因子為976.254，應力強度因子為814.264。與《應力強度因子手冊》的計算結果進行對比，發現其相對誤差為2.68%。

6 結語

該文通過考慮重力、裂隙水壓力和地震力的影響，建立了巖石工程中常見的滑塌式危巖力學模型。此外，通過斷裂力學得到了Ⅰ-Ⅱ復合應力強度因子。根據最大周向應力理論，通過三角形萬能公式計算得出了理論斷裂角。對防災減災和工程安全評價具有一定的理論指導意義和經濟價值。

參考文獻

[1] Nara Y，Oe Y，Murata S，et al.Estimation of Long-Term Strength of Rock Based on Subcritical Crack Growth[M].Springer International Publishing，2015：2157-2160.

[2] Zygouri V，Koukouvelas I K.Evolution of rock falls in the Northern part of the Peloponnese， Greece[C]//IOP Conference Series：Earth and Environmental Science.2015.

[3] Chen H K，Zhou Y T，Wang Z.Study on Damage Characteristics of Unstable Rocks under Excitation Effect[J].Applied Mechanics and Materials，2013（459）：575-581.

[4] Johari A，Momeni M，Javadi A A.An Analytical Solution For Reliability Assessment Of Pseudostatic Stability Of Rock Slopes Using Jointly Distributed Random Variables Method[J].Iranian Journal of Science and Technology Transactions of Civil Engineering， 2015（39）：351-363.

[5] Li Y，Zhou H，Zhu W，et al.Numerical Study on Crack Propagation in Brittle Jointed Rock Mass Influenced by Fracture Water Pressure[J]. Materials，2015，8（6）：3364-3376.

[6] Liang L，Xiong J，Liu X.Experimental study on crack propagation in shale formations considering hydration and wettability[J]. Journal of Natural Gas Science and Engineering，2015（23）：492-499.

[7] Westergaard H M W.Bearing Pressures and Cracks[J].J of Applied Mechunies，1939（6）：A49-A53.

[8] Erdogan F，Sih G C.On the crack extension in plates under plane loading and transverse shear[J].Journal of basic engineering，1963， 85（4）：519-525.