汽輪機座缸式軸承振動影響因素研究
高慶水, 劉 石, 張 楚
(廣東電網公司 電力科學研究院,廣州 510080)
大型汽輪機低壓缸兩側軸承座有落地式和座缸式兩種。座缸式軸承位于排汽缸擴壓器洼窩中,轉子和汽缸自重、真空載荷等通過軸承座傳遞到汽缸殼體,再經汽缸下部裙部支撐傳遞到基礎上。這類機組軸系短,結構緊湊,在大型汽輪機上得到廣泛應用。然而近年來很多機組座缸式軸承振動較大[1-2],還出現了軸承振動比轉軸振動大的異常現象。某臺1 000 MW汽輪機臺板和地基振動小于0.015 mm,而軸承振動達到0.044 mm,低壓缸振動達到0.080 mm,異常振動嚴重影響了機組安全運行。
與落地式軸承相比,座缸式軸承支撐剛度較小,缸體變形等因素對支撐剛度影響較大[3-6],振動分析時需要考慮轉子-軸承-支撐系統耦合特性[7]。模態綜合法[8-10]和阻抗匹配法[11]是兩種常用的耦合分析方法。這2種方法將基礎視為由多個集中質量塊所組成的復雜結構,經模態分析后按相應準則組合為整體系統。汽輪發電機組基礎振動較小,可以將基礎影響用軸承座參振質量和支撐剛度來表示[12],總體剛度由支撐剛度和油膜剛度串聯構成。這種模型比較簡單,不考慮油膜交叉剛度特性,也不考慮支撐剛度對系統等效阻尼的影響。
本文將軸承油膜特性用剛度、阻尼系數來表示,考慮支撐影響后建立了軸承-支撐系統等效動力模型,研究了某大型汽輪機低壓轉子振動特性和影響因素,對實際振動故障進行了綜合分析。
1 支撐系統影響等效分析模型
圖1給出了轉子-軸承-支撐系統模型。油膜特性用剛度、阻尼系數表示,汽缸支撐用軸承座質量和支撐剛度來反映。軸承座運動方程為:
(1)
式中:m2為軸承座參振質量;kij,cij,i,j=x,y為油膜剛度和阻尼系數;kx,ky為水平和垂直支撐剛度;x1,2,y1,2為軸頸和軸承座水平和垂直位移。
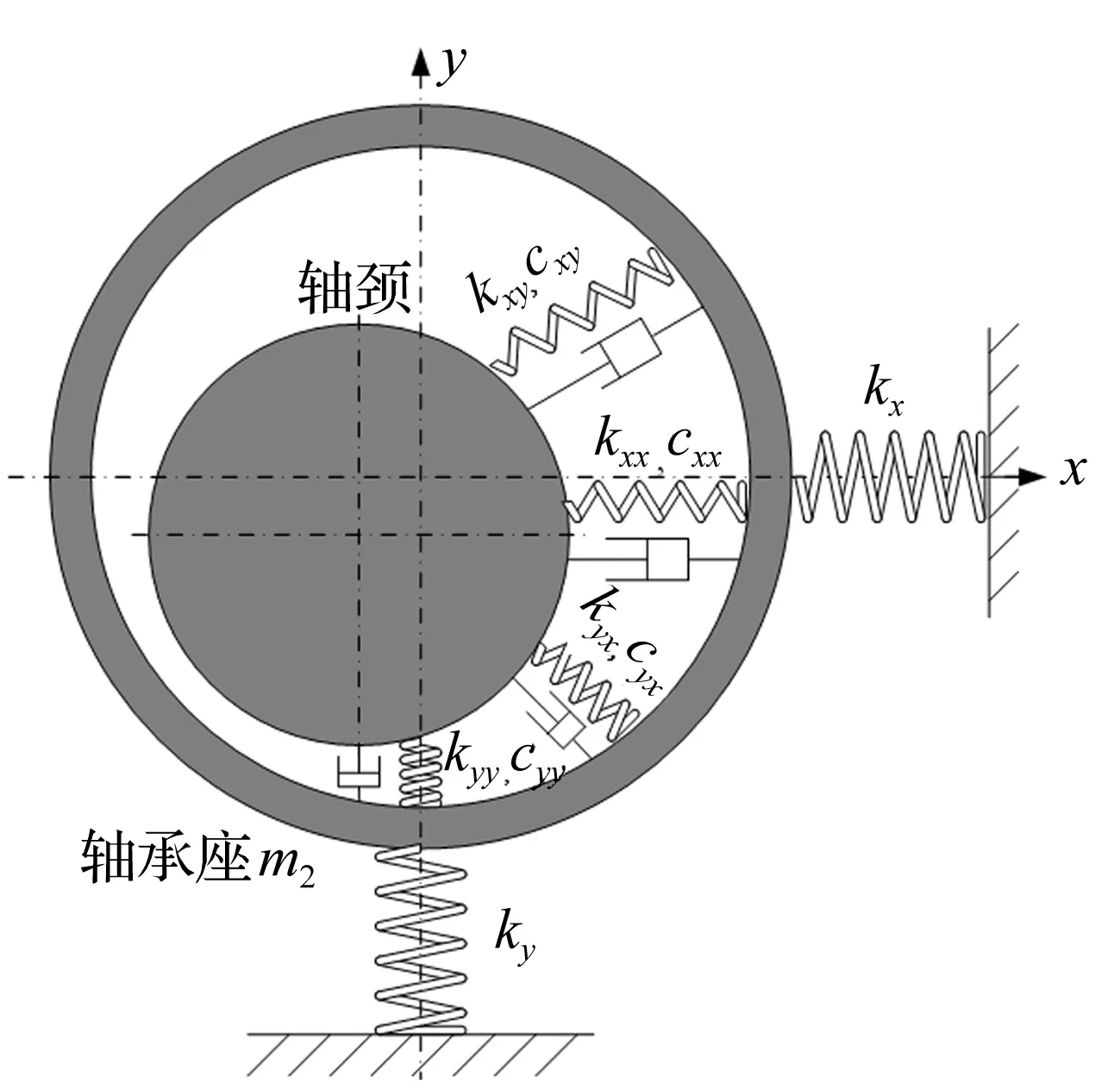
圖1 支撐系統分析模型
頻率為ω的不平衡力激勵下系統響應為:
x1,2=X1,2eiωt,y1,2=Y1,2eiωt
(2)
式中:X1,2,Y1,2為軸頸和軸承座振動位移幅值。
將式(2)代入式(1)得
(3)
由式(3)可得
(4)
式中:αij為軸振和瓦振之間的關系系數。
軸頸受到的油膜力fx,y為
(5)
令fx,y=Fx,yeiωt,Fx,y為油膜力幅值,將式(2)代入式(5)得
(6)
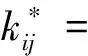
i,j=x,y
(7)
從上式可見,支撐剛度對系統等效剛度和等效阻尼都會產生影響。
2 支撐剛度對軸承動力特性影響分析
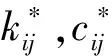
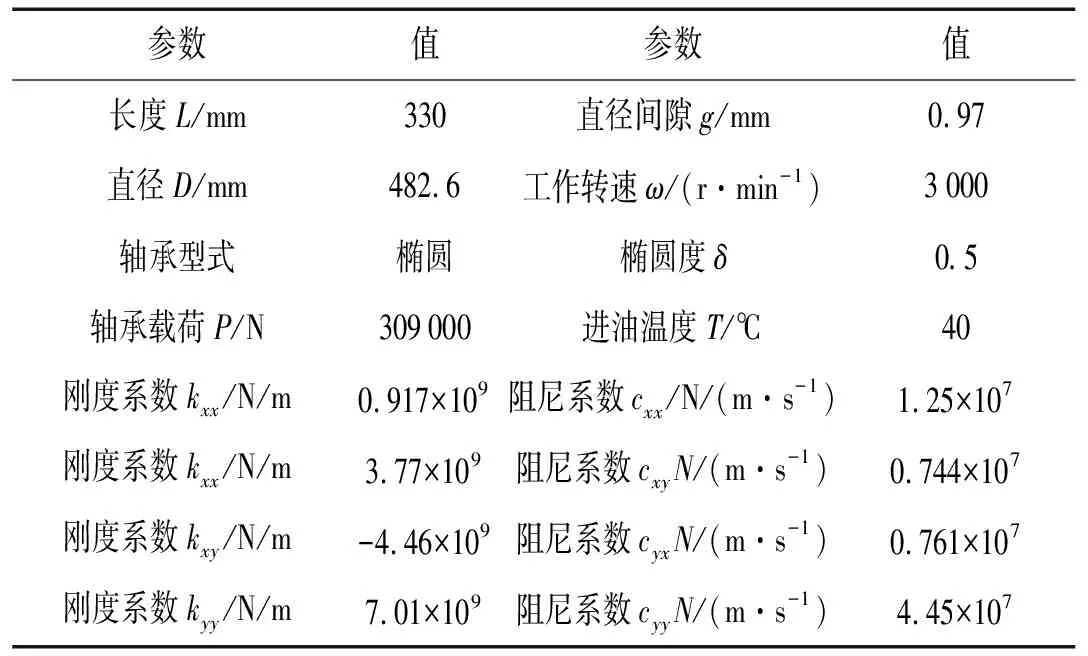
表1 軸承參數
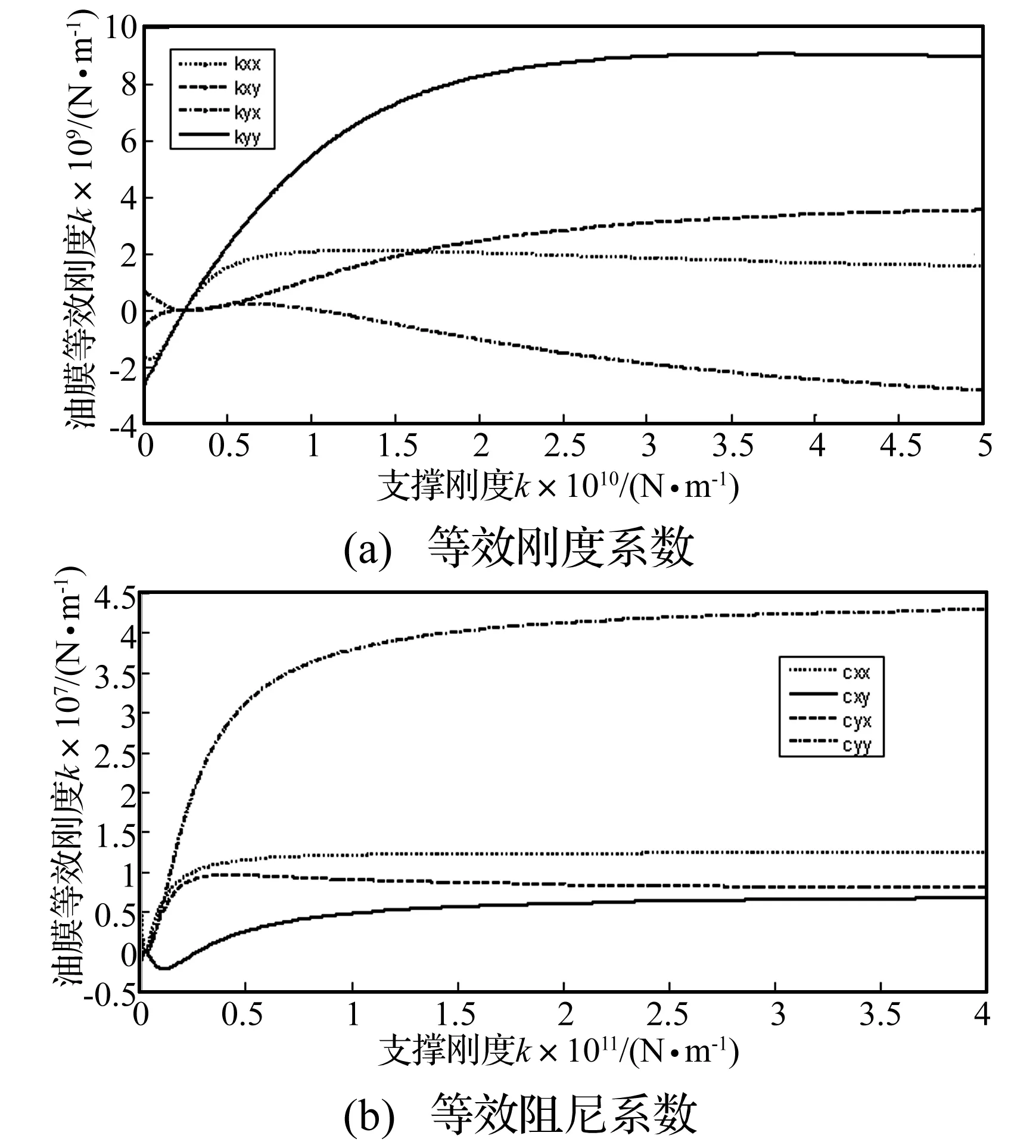
圖2 等效剛度和阻尼系數隨支撐剛度變化情況
圖2給出了系統等效剛度和阻尼系數隨支撐剛度變化情況,支撐剛度對系統等效剛度和等效阻尼系數都會產生較大影響。支撐剛度大于1.5×1010N/m后,支撐剛度對系統等效剛度和阻尼的影響較小;支撐剛度小于1.5×1010N/m時,隨著支撐剛度的降低,系統等效剛度和阻尼系數幅值下降很快,垂直和水平等效主剛度甚至變為負,這將對轉子-軸承系統動力特性產生很大影響,軸承座振動將會很大。
計算和實測表明[3-6],大型汽輪機組低壓缸剛度在109N/m~1010N/m之間。對于本例而言,正好處于支撐剛度影響敏感區內。
3 某大型汽輪機低壓轉子振動分析
3.1 數學模型
圖3給出了某大型汽輪機組轉子-軸承系統動力學分析模型。高壓轉子兩側軸承為落地式,可不考慮支撐剛度影響。包含軸承油膜各向異性情況下的轉子—軸承系統動力學方程為[12]:
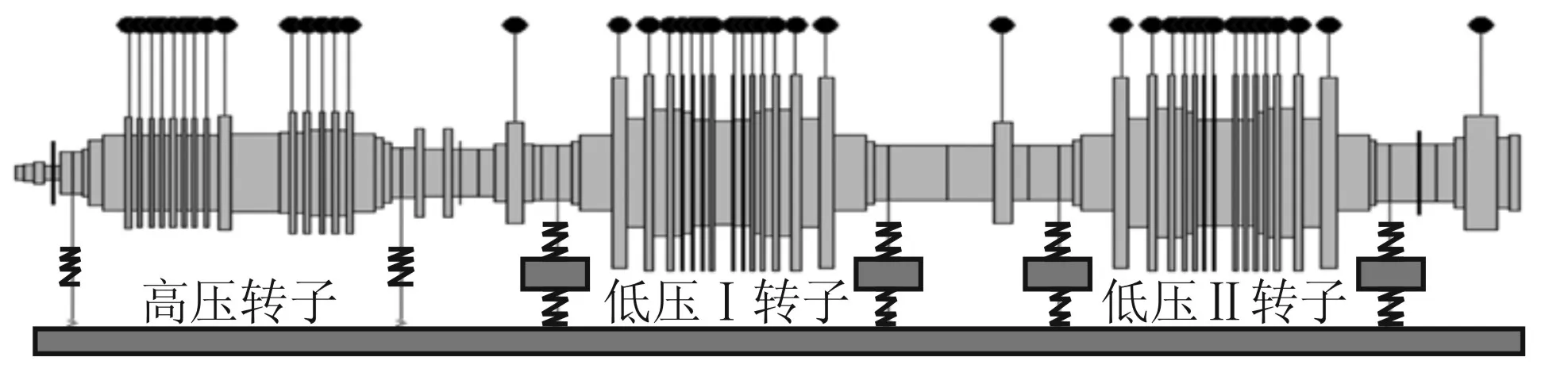
圖3 轉子-軸承系統動力學模型
(8)
式中:M1、K1和G1為整體質量矩陣、剛度矩陣和回轉矩陣[12];
cij、kij為考慮支撐剛度影響后整體油膜等效阻尼和剛度矩陣;
U1,U2為系統位移向量
U1={x1θy1x2θy2…xnθyn}T
U2={y1-θx1y2-θx2…ynθxn}T
Q為不平衡力向量
(9)
式中:{Qc,s}為不平衡力向量中余弦和正弦分量值。設
(10)
式中:A1,A2,B1,B2為不平衡響應中余弦和正弦量值。
將式(9)和(10)代入式(8),得
(11)
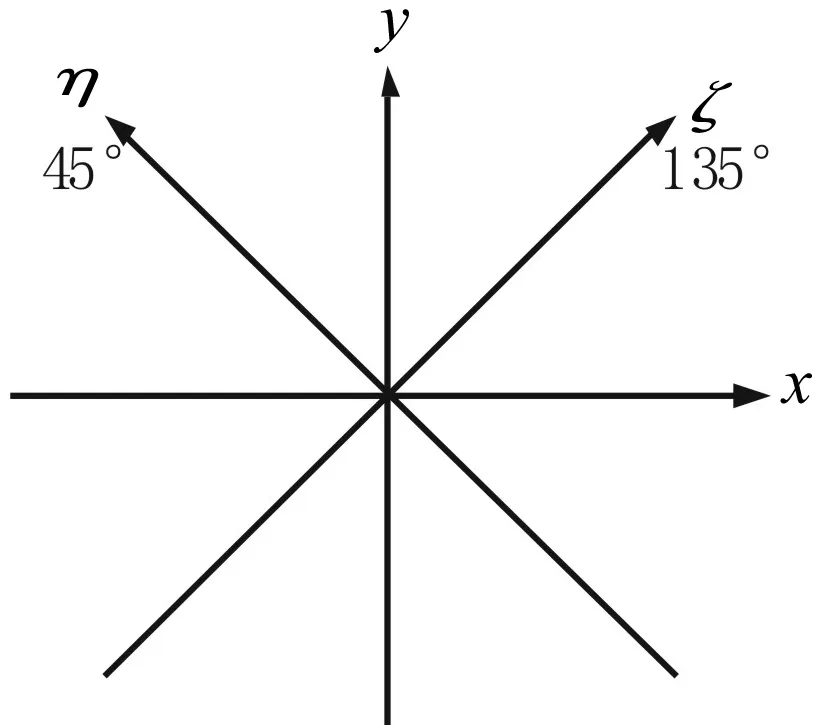
圖4 軸振傳感器坐標變換示意圖
求出轉軸絕對振動X1,Y1后,代入式(4)可求得軸承座振動X2,Y2,兩者相減可以求得軸相對振動X3,Y3。
汽輪機軸振探頭通常安裝在如圖4所示的45°和135°方向,而軸承座振動探頭通常安裝在垂直和水平方向上,可以通過坐標變換將其轉換到同一坐標系下分析。設軸振坐標為ξ,η,該坐標下的振動與垂直和水平振動之間的關系為:
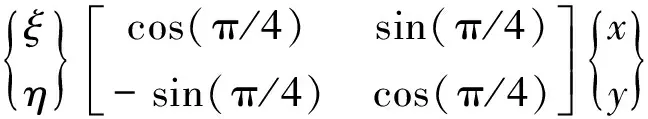
(13)
低壓轉子第3階臨界轉速通常遠高于工作轉速,不平衡響應分析可以只考慮前兩階模態影響。計算時在低壓轉子兩端末級葉輪處設置一組力偶,在中間葉輪處設置一組力。
3.2 支撐剛度對升速過程中振動影響分析
圖5給出了不同支撐剛度下#3軸承軸絕對振動隨轉速變化情況。垂直和水平振動特性相似,現以水平軸振為例分析如下:
(1) 支撐剛度為1×1010N/m時,計算轉速范圍內沒有出現共振峰值,升速過程中振動較小。
(2) 隨著支撐剛度的降低,臨界轉速降低。支撐剛度降到2×109N/m時,臨界轉速已經下降到3 000 r/min以內。兩個共振峰值所對應轉速分別為轉子第1階和第2階臨界轉速。
(3) 支撐剛度降到1.2×109N/m時,臨界轉速進一步降低,共振轉速下不僅幅值大,而且共振峰較尖。在支撐彈性作用下系統等效阻尼減小,對共振峰值的抑制作用減弱。
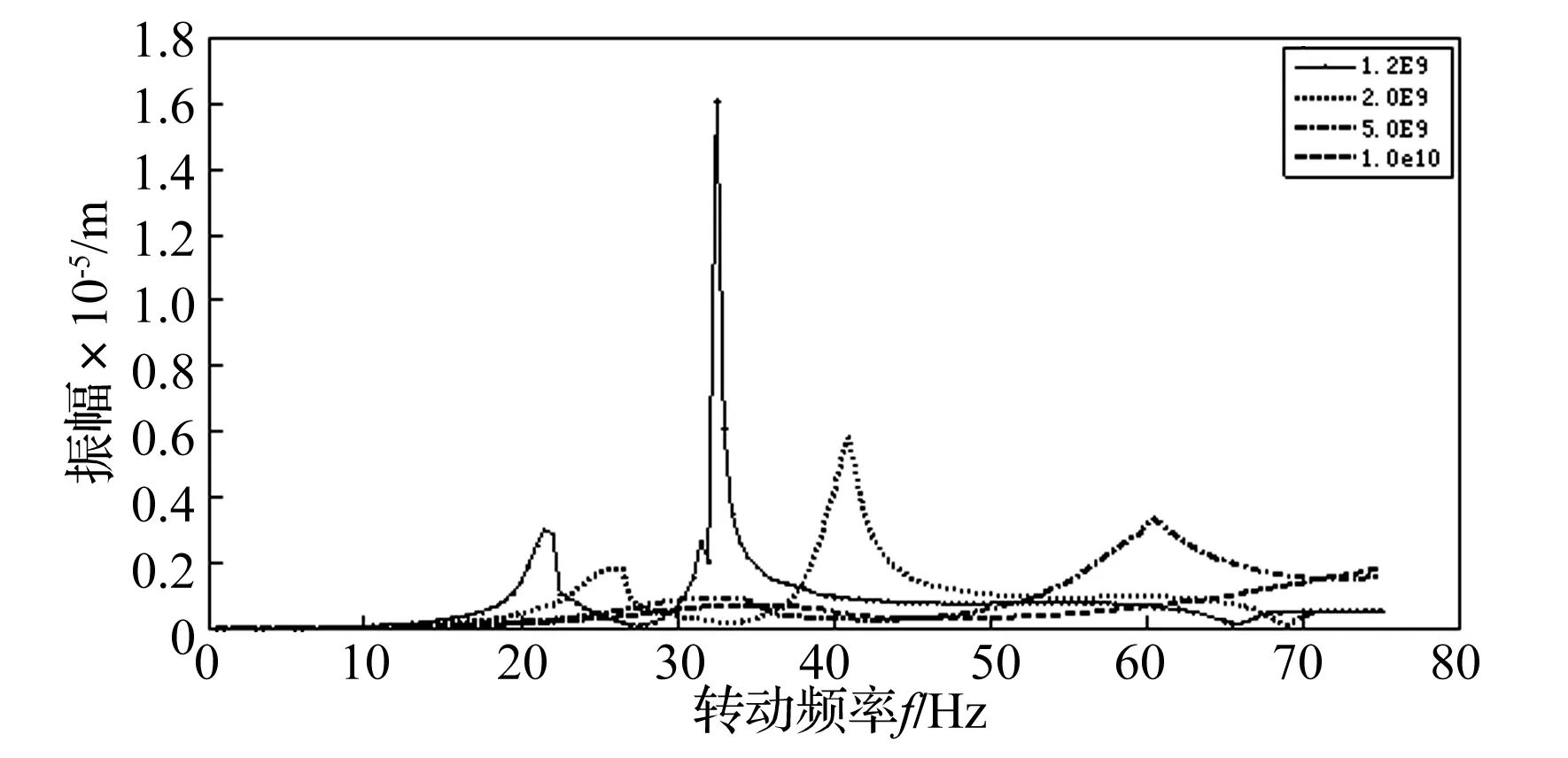
圖5 不同支撐剛度下轉軸振動隨轉速變化情況
3.3 不同支撐剛度下軸振/瓦振之間的幅值關系
圖6給出了不同支撐剛度下軸振和瓦振隨轉速變化情況。不同支撐剛度下振動特性不同,軸振/瓦振關系差異較大。支撐剛度大時,升速過程中瓦振較小,軸振較大,絕對軸振和相對軸振近似相等。支撐剛度小時,升速過程中相對軸振較小,瓦振很大,絕對軸振和瓦振近似相等。
不同支撐剛度下,絕對軸振都能夠較為準確地反映轉子實際振動情況。對于低壓轉子而言,只監測相對軸振并不合理。
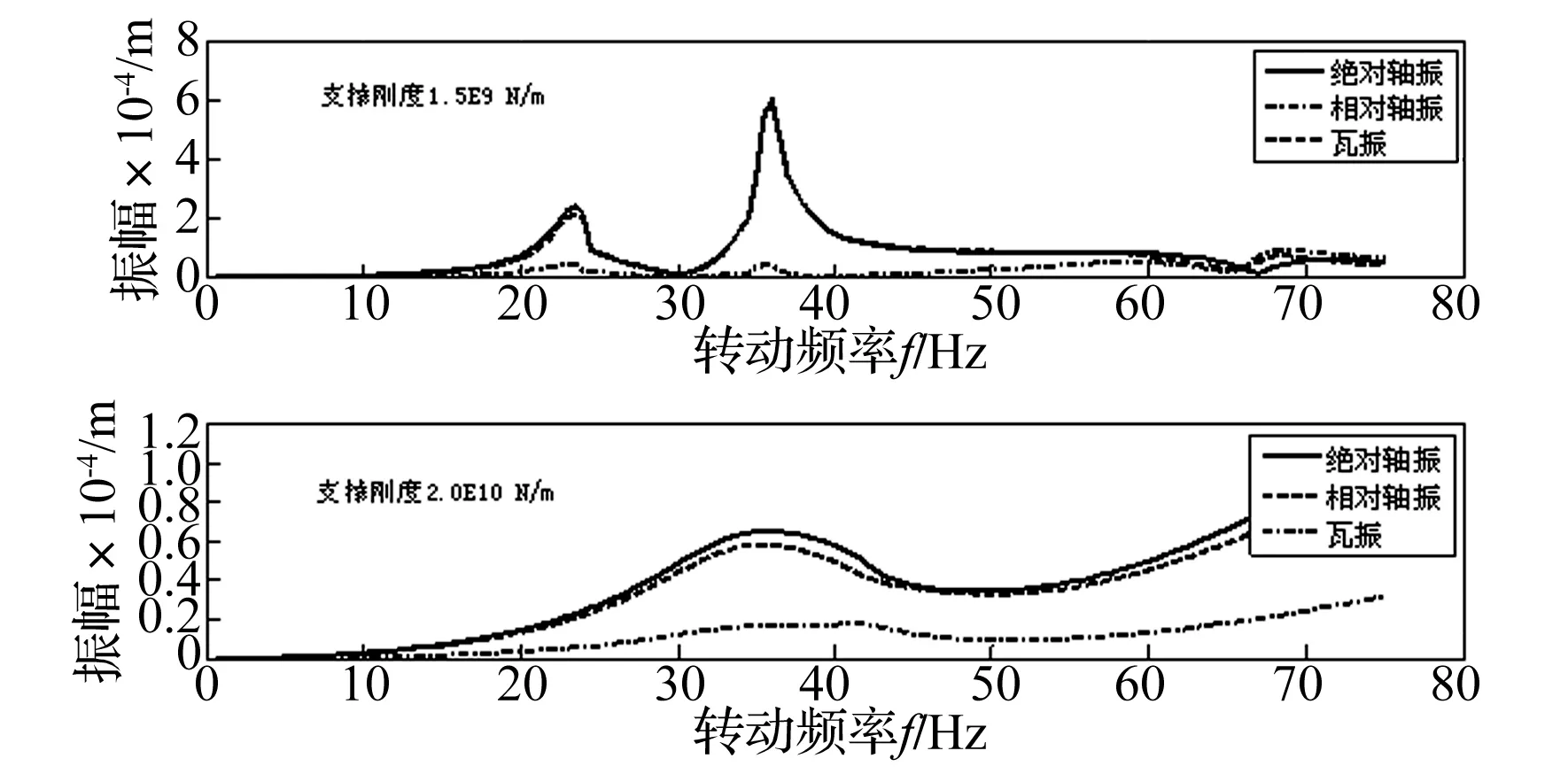
圖6 不同支撐剛度下軸振和瓦振隨轉速變化情況
3.4 不同支撐剛度下軸振/瓦振之間的相位關系
大量觀點認為,軸振和瓦振都反映了軸承振動情況,其相位應該相近。圖7給出了不同支撐剛度下軸振、瓦振相位隨轉速變化情況。受支撐剛度影響,兩者之間的相位關系實際上比較復雜。
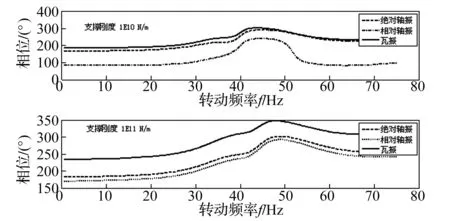
圖7 不同支撐剛度下軸振和瓦振之間的相位關系
(1) 支撐剛度小時,升速過程中絕對軸振和瓦振相位基本相同,相對軸振和瓦振相位相差了60°~150°;
(2) 支撐剛度大時,升速過程中絕對軸振和相對軸振相位基本相同,軸振和瓦振相位相差了約50°。
4 大型汽輪機組實際振動分析
某臺1000 MW大型汽輪機組軸系由高、中壓轉子和兩個低壓轉子組成。高、中壓轉子為落地軸承,低壓轉子為座缸式軸承。實測表明,3 000 r/min下低壓轉子兩側軸承座振動達到45 μm ~50 μm,處于合格邊緣,但是軸振優秀,轉軸最大振動只有76 μm。
在現場開展了低壓轉子動平衡試驗,表2和表3分別給出了低壓Ⅱ轉子和低壓Ⅰ轉子動平衡試驗數據。為了能夠與瓦振影響系數相比,表中所給出的垂直方向絕對軸振和相對軸振影響系數已經過坐標變換,轉換到垂直方向。
由加重前后振動數據可以計算出影響系數:
(14)
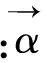
影響系數反映了在轉子兩端分別加1 kg∠0°和1 kg∠180°配重后的振動響應。
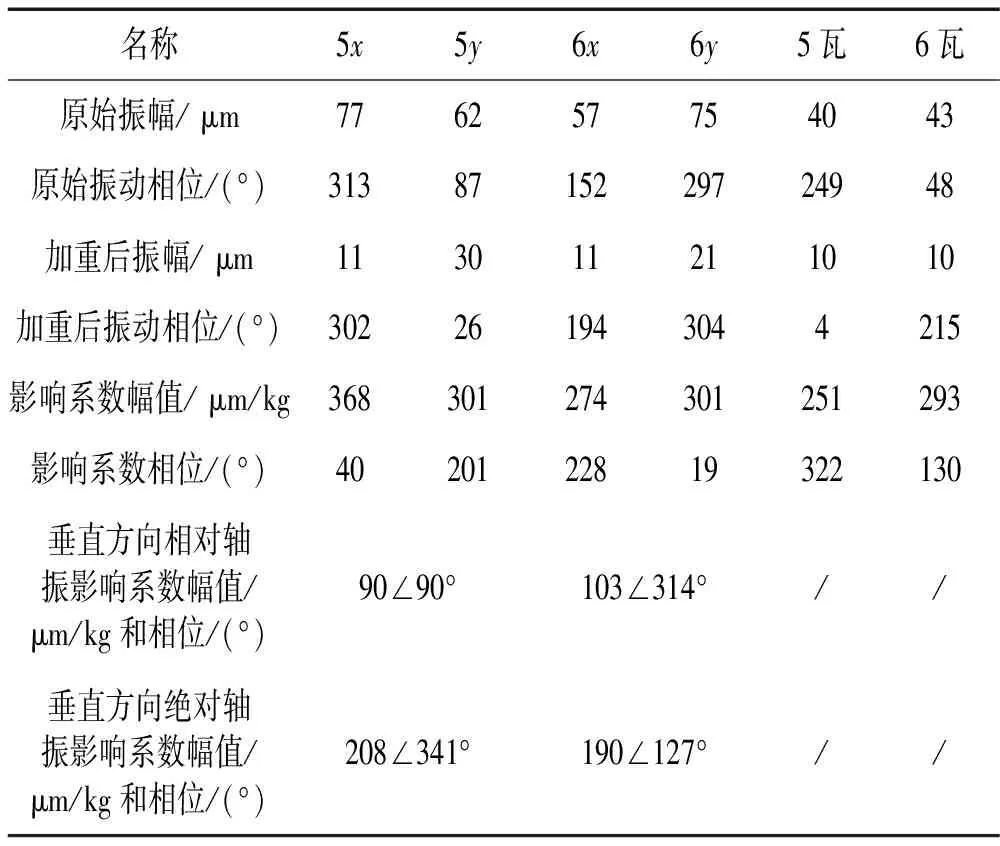
表2 低壓轉子Ⅱ動平衡數據
在低壓Ⅱ轉子兩側加反對稱平衡配重后,相對軸振影響系數幅值較小,相位和瓦振影響系數相位相差130°~180°,絕對軸振影響系數和瓦振影響系數幅值相近、相位相近,分析表明低壓Ⅱ轉子兩側座缸式軸承的支撐剛度較弱。
表3給出了低壓Ⅰ轉子加重前后振動數據。在低壓轉子Ⅰ兩側加反對稱平衡配重后,垂直方向上相對軸振影響系數相位和瓦振影響系數相位相近,瓦振影響系數幅值較小,垂直方向絕對軸振和相對軸振影響系數幅值相近,說明低壓Ⅰ轉子兩側座缸式軸承的支撐剛度較強。
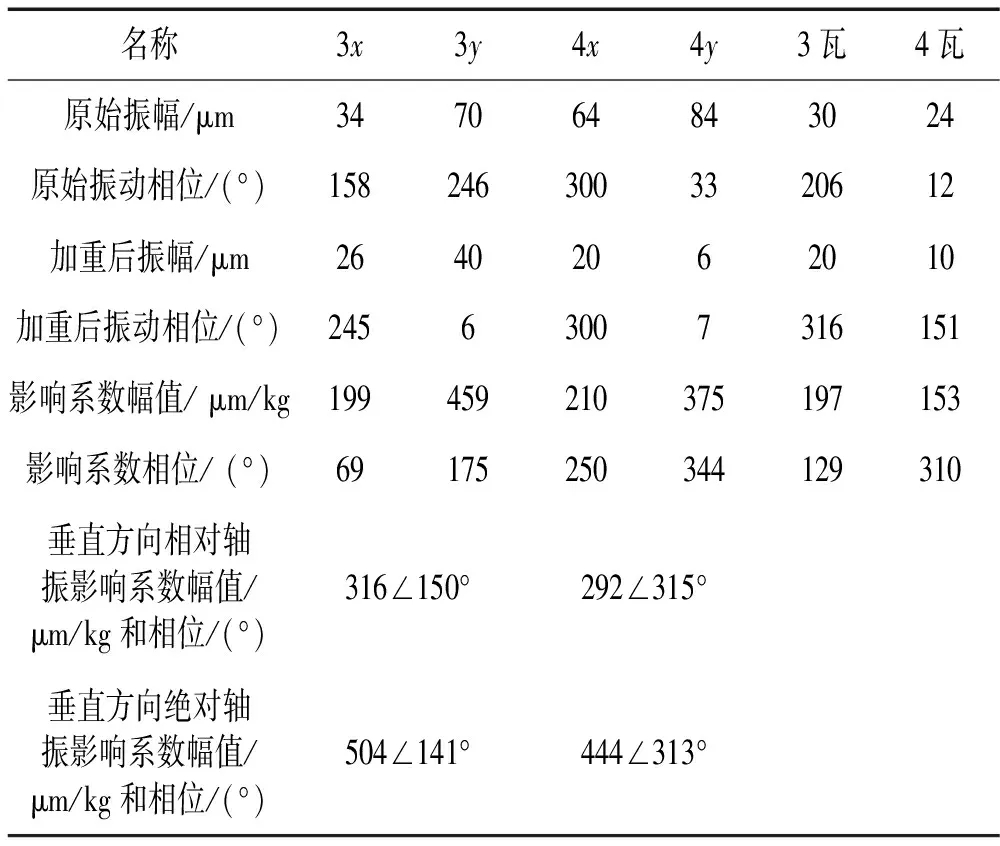
表3 低壓Ⅰ轉子動平衡數據
該型汽輪機兩個低壓缸結構相同,振動現象不完全相同。很多人認為振動大是由于低壓缸共振引起的。同一臺機組結構相同的兩個汽缸的共振特性不可能有如此大的差別。分析表明,不同安裝狀態下低壓缸裙部與基礎臺板之間的接觸狀況不同,座缸式軸承的支撐剛度不同,因而振動特性不同。
5 結 論
(1) 大型汽輪機低壓轉子兩側座缸式軸承振動分析必須考慮支撐剛度影響,本文所提出的等效模型簡單方便。
(2) 支撐剛度會同時影響系統等效剛度和等效阻尼。不同支撐剛度下系統振動特性不同。彈性支撐下,軸振和瓦振之間相位差可能較大。支撐特性可以根據絕對軸振、相對軸振和瓦振幅值和相位之間的關系進行分析。
(3) 座缸式軸承監測絕對軸振比監測相對軸振更有意義。座缸式軸承振動受不平衡力的影響較大,可以通過精細動平衡降低振動。
[1] 張學延,史建良,李德勇. 國產600MW汽輪發電機組振動問題分析及治理[J]. 熱力發電,2009,38(9):1-6.
ZHANG Xue-yan, SHI Jian-liang, LI De-yong. Analysis and treatment of vibration for 600MW turbogenerator unit made in China[J]. Thermal Power,2009,38(9):1-6.
[2] 郭玉杰,張文濤,劉占輝,等.真空變化對大型汽輪發電機組軸承標高和振動的影響分析[J].電站系統工程,2012,28(3):50-52.
GUO Yu-jie, ZHANG Wen-tao, LIU Zhang-hui, et al. Influence analysis of cylinder vacuum on bearing elevation and vibration[J]. Power System Engineering,2012,28(3):50-52.
[3] 石可重,李延波,武新華,等. 排汽缸剛度有限元分析[J].汽輪機技術,2001,43(6):344-346.
SHI Ke-zhong, LI Yan-bo, WU Xin-hua, et al. The rigidity analysis of LP cylinder with limited element calculation[J]. Turbine Technology,2001,43(6):344-346.
[4] 杜連秀,張偉忠. 汽輪機低壓缸剛性有限元分析[J].汽輪機技術,2005,47(6):428-429.
DU Lian-xiu, ZHANG Wei-zhong. Analysis of turbine LP with FEA[J]. Turbine Technology,2005,47(6):428-429.
[5] 單世超,陳伯樹,平路光. 大型汽輪機軸承支撐剛度研究[J]. 汽輪機技術,2012,54(3):201-203.
SHAN Shi-chao, CHEN Bo-shu, PING Lu-guang. Research of stiffness of the bearing support for large steam turbine[J]. Turbine Technology,2012,54(3):201-203.
[6] 孫慶,李汪繁,王秀瑾. 600MW超臨界空冷機組基礎及軸承座剛度研究[J]. 發電設備,2012,26(4):217-221.
SUN Qing, LI Wang-fan, WANG Xiu-jin. Research on stiffness of foundation and bearing pedestal for 600MW supercritical air-cooling unit[J]. Power Equipment,2012,26(4):217-221.
[7] 張宇,陳宇恕,畢勤勝. 轉子-軸承-基礎非線性動力學研究[J].振動工程學報,1998,11(1):24-30.
ZHANG Yu, CHEN Yu-shu, BI Qin-sheng. Nonlinear dynamic analysis of rotor-bearing-foundation system[J]. Journal of Vibration Engineering,1998,11(1):24-30.
[8] Cavala K L, Cavalcante P F, Okabe E P. An investigation on the influence of the supporting structure on the dynamics of the rotor system[J]. Mechanical Systems and Signal Processing,2005,(19):157-174.
[9] Paolo P, Nicolo B, Andrea V. Use of modal representation for the supporting structure in model-based fault identification of large rotating machinery: part I-theoretical remarks[J]. Mechanical Systems and Signal Processing, 2006,(20): 662-681.
[10] Chen Yeong-shu, Cheng Ye-dar, Yang Ta-chung, et al. Accurate identification of the frequency response functions for the rotor-bearing-foundation system using the modified pseudo mode shape method[J]. Journal of Sound and Vibration,2010,329:644-658.
[11] Bonello P, Brennan M J. Modeling the dynamic behavior of a supercritical rotor on a flexible foundation using the mechanical impedance technique[J]. Journal of Sound and Vibration,2001,239(3):445-466.
[12] 鐘一諤,河衍宗,王正,等.轉子動力學[M].北京:清華大學出版社,1987.

