旋翼柔性梁結構扭轉剛度特性分析

張旺亮，石偉興

(1.中航直升機有限責任公司, 天津 300308；2.中國兵器工業計算機應用技術研究所，北京 100089)

旋翼柔性梁結構扭轉剛度特性分析

張旺亮1，石偉興2

(1.中航直升機有限責任公司, 天津 300308；2.中國兵器工業計算機應用技術研究所，北京 100089)

旋翼柔性梁是整個無軸承旋翼的核心部件，柔性梁在承受巨大的離心力的同時還要滿足揮舞、擺振以及變距的剛度要求。由于柔性梁結構不存在實際的變距鉸，旋翼的變距操縱要靠柔性梁結構的大變形扭轉實現，纖維復合材料可裁剪設計的特性正好滿足了這一要求。文章主要針對柔性梁結構的扭轉剛度進行了分析計算，分析了八種特殊界面的扭轉剛度，比較了復合材料與金屬材料的扭轉剛度，得出的結論可以為工程上柔性梁的扭轉剛度設計提供參考。

柔性梁；扭轉剛度；多截面；復合材料槳轂

0 引言

隨著先進材料技術的發展，直升機旋翼槳轂越來越多地采用更為簡潔的無鉸式或無軸承式結構，結構通常采用柔性梁的形式[1]。柔性梁是典型的懸臂梁結構，槳葉的揮舞運動由柔性梁的彎曲變形承擔，槳葉的變距運動則由柔性梁的扭轉變形承擔，變距拉桿將扭矩作用于柔性梁套管，柔性梁套管在柔性梁扭轉變形的配合下實現槳葉的變距。西科斯基的RAH-66槳轂以及歐直EC-135旋翼的結構就采用了復合材料柔性梁結構(見圖1)，其復合材料柔性梁位于中央，負責扭轉以及揮舞運動，柔性梁外面有復合材料變距套管，套管同時也具有整流減阻的作用[2]。

柔性梁是無軸承旋翼系統的核心部件，柔性梁結構件的扭轉剛度要求盡可能地小，以滿足槳葉扭轉運動所需的自由度。在具備較低扭轉剛度的情況下，還要滿足旋轉離心力的抗拉剛度與強度要求，適應揮舞、擺振運動的動力學特性要求。與此同時，槳葉的揮舞、變距以及擺振運動的區別不再那么明顯，旋翼工作過程中將產生不同于全鉸式旋翼的彎-扭氣動耦合現象，這對旋翼的氣動特性也帶來了新的不確定影響。實際工程應用中，多截面結構在節約材料、節約空間等方面也有較多運用，例如MBB公司BO-105驗證旋翼的柔性梁采用的就是典型的雙截面結構[5]。本文針對幾種典型截面柔性懸臂梁結構的扭轉剛度進行了分析。

在柔性梁的結構設計過程中，單截面柔性梁的幾何選擇主要依據鐵木辛柯彈性理論。彈性理論主要分析了圓截面等簡單截面的扭轉剛度。根據彈性理論，簡單單連通截面的扭轉剛度表達式可以很容易推導出來，這里不再贅述。上述理論的局限性在于，對多連通復雜截面以及更復雜的截面的扭轉剛度沒有過多涉及，缺乏有效的試驗與有限元數據。

因此，對于多截面剛度特性的探究，其方法除了理論與試驗以外，有限元方法不失為一種最簡便的方法。本文將具體敘述九種不同形狀的截面的扭轉剛度的有限元分析結果，從而探究最小扭轉剛度截面的選擇。

1 多截面扭轉剛度計算

根據材料力學相關理論，材料的扭轉變形主要是材料截面上切應力作用的結果，對于各向同性材料的扭轉變形，有以下微分關系：

(1)

即材料的扭轉剛度主要受到材料常數G和截面形狀IP的影響。對于各向同性材料，當材料的楊氏模量E和泊松比υ確定后，其材料常數G基本確定；而對于纖維復合材料，隨著鋪層順序和鋪層方向的不同，其宏觀材料常數G12是變化的。很顯然，G12越小，其宏觀材料的扭轉剛度也越小。理論和試驗表明，單向纖維復合材料的G12最小，在扭轉變形過程中，扭轉變形產生的切應力僅分布在材料截面上，而纖維方向垂直于材料截面(如圖2所示)。

對于截面形狀對扭轉剛度的影響，鐵木辛柯彈性理論主要討論了圓截面、橢圓截面、三角形截面、工字形等單連通截面的扭轉變形[7]，對多連通截面的扭轉剛度沒有涉及。本文采用ANSYS方法計算較復雜截面的扭轉剛度大小。扭轉剛度試驗所選取的不同形狀的截面如圖3所示。材料選用各向同性材料鋁合金，施加扭矩的力臂長度為108mm，施加的力矩分別為2.16、4.05、5.13、6.21、6.804、7.884、9.234N·m共七組。本計算對象截面面積均為100m2，有效扭轉長度均為150mm，其截面形狀如圖3所示，共九種不同形狀。

根據控制變量的試驗要求，本文計算與試驗的對象1-8號截面均保持橫截面積不變，并且均以相同面積的圓截面作為比較對象。有限元計算模型與計算結果如圖4所示，以8號截面為例。

在此之前我們做了圓截面與矩形截面的有限元計算結果與理論計算結果的對比，計算結果如表1所示。

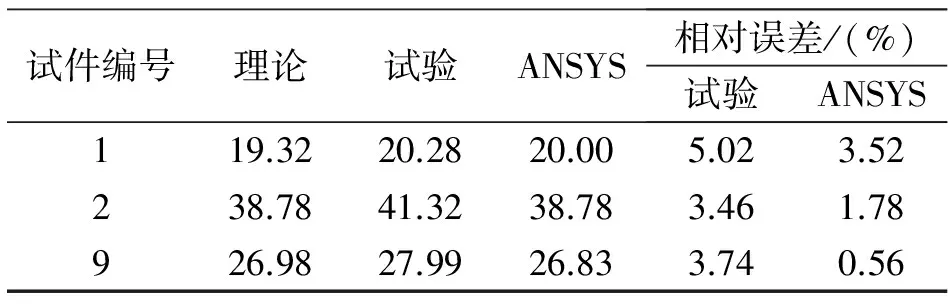
表1 圓截面與矩形截面扭轉剛度分析結果(Nm3/rad)

由以上計算與試驗結果可以看出，ANSYS計算結果與扭轉理論計算結果更為接近，試驗結果也佐證了理論分析與有限元結果的可靠性。基于此，下文主要利用有限元手段分析比較了其他復雜界面的扭轉剛度大小。根據鐵木辛柯扭轉剛度理論，施加扭矩大小及梯度保持不變的情況下，本文用Tl/φ的值表示截面扭轉剛度的大小。截面扭轉剛度ANSYS計算結果對比如圖5所示，扭轉剛度用角位移表示。

可以看出，不同截面扭轉剛度的大小與其截面形狀是密切相關的。由以上計算結果我們可以看到，8號截面具有最小的扭轉剛度，與同樣截面面積的圓截面相比，其扭轉剛度減小可達約2.5倍以上。

扭轉剛度計算結果表明，與其他截面相比，背對背“雙-T”型的截面具有較小的扭轉剛度。下節重點分析背對背“雙-T”型截面的彎曲、扭轉剛度的特性，為柔性梁的截面選擇與設計提供幫助。

2 復合材料梁結構扭轉剛度分析

上文的分析結果顯示“雙T”型截面在減小截面扭轉剛度方面具有明顯優勢，下面是針對復合材料剪裁鋪層的柔性梁結構進行的扭轉剛度有限元分析的結果。材料選用的是T300/5208，探究截面形狀對結構扭轉剛度的影響，材料參數由表2給出。

表2 T300/5208材料的基本力學性能

柔性梁長L=260mm，單層碳纖布厚度為0.5mm，內部鋪層為沿展向0°鋪層，共6層，外表面蒙皮鋪層為兩層±45°鋪層。梁截面基本尺寸與基本鋪層設計如圖6所示。

通過建立有限元模型，并利用前文中同樣的分析方法，在梁的端部施加大小為8.5N·m的扭矩，從而計算梁的扭轉變形情況。表3列出的是計算結果。圖7是有限元模型與等效應力計算結果的云圖顯示。

表3 ANSYS應力、位移計算結果峰值列表

由以上計算結果可知，復合材料各向異性對降低結構扭轉剛度效果明顯，結構應力與位移均發生了明顯的變化。

1)結構扭轉變形時，各單元的拉壓應力同時存在，內層的等效應力大于外層，且以壓應力為主，當柔性梁承受離心力載荷時，可以部分抵消壓應力的存在。

2)τxy、τxz在截面的表面處的值大于截面內部，且上下表面切應力方向正好相反，用±45°的外表面鋪層來抵抗剪力作用以保護內部的單向纖維是必要的。

3)圖7所示為結構扭轉變形的情況，變形主要是端面處Y、Z方向的線位移和繞X軸的角位移。表3所列的最大單元扭轉變形為0.544rad，端部截面結構扭轉變形大于30°。

3 結論

本文通過有限元分析計算的手段，主要對柔性梁截面扭轉剛度特性進行了分析，可以得到以下幾點結論：

1)扭轉剛度計算結果表明，在所選的九種多截面形式中，背對背“雙-T”型截面具有較小的扭轉剛度，此結論可為柔性梁的截面選擇與設計提供幫助。

2)采用纖維復合材料鋪層的柔性梁，由于其剛度可設計性的特點，同等截面情況下，其扭轉剛度大大減小。

以上相關結論可幫助我們進行無軸承旋翼柔性梁的結構設計，無軸承槳轂結構中，小的扭轉剛度意味著旋翼操縱特性的提高。同時，槳轂扭轉剛度的確定也要和截面其他兩個方向的彎曲剛度(揮舞、擺振剛度)進行協調。對于具體的柔性梁結構，小的扭轉剛度常常伴隨著小的揮舞剛度，而此時擺振方向的剛度是比較大的。在工程設計中，可對柔性梁截面形狀進行分段剛度設計，如在槳轂根部附近盡量適應扭轉剛度和揮舞剛度，而在槳轂端部附近可盡量適應擺振剛度的調整，這樣柔性梁段可同時滿足三個方向的剛度需求。在柔性梁動力學分析與設計中，改變截面的剛度可很好地調整旋翼系統的揮舞、擺振頻率的變化，同時對改變振動過程中彎-扭耦合的影響也有幫助。

[1] 李滿福, 陳錦濤, 王清龍. 國外旋翼槳轂構型技術綜述[J]. 直升機技術, 2010(4): 64-70

[2] Wang J M. Theoretical and Experiment a1 Research in Aeroelastic Stability of an Advanced Bearingless Rotor for future Helicopters[C]． AIAA 91-0192, 29th Aerospace Sciences Meeting, January 7-10, 1991/Reno, Nevada.

[3] 楊乃賓, 倪先平. 直升機復合材料結構設計[M]. 北京: 國防工業出版社, 2008.

[4] Bernhard A P F, Chopra I. Analysis of a Bending-Torsion Coupled Actuator for a Smart Rotor with Active Blade Tips[J]. Smart Materials and Structures, 2001(10): 35-52.

[5] 沈觀林, 胡更開, 劉 彬. 復合材料力學(第2版)[M]. 北京: 清華大學出版社出版社, 2013.

[6] Nakadate M, Tgguchi H, Takaki J．Design and Test Evaluation of FBR Bearingless Main Rotor[J]. Journal of American Helico pter Society, 2001,46( 2):107-116.

[7] 鐵木辛柯S P, 古地兒J N, 著，徐芝綸，譯. 彈性理論[M]. 北京: 高等教育出版社, 2013.

[8] Gessow A, Myers G C, JR． Aerodynamics of the helicopter[M]．New York: Frederick ungar publishing CO. Eighth Printing, 1985.

[9] 馬兵林. 星形柔性旋翼槳葉固有振動特性工程計算方法[J]. 直升機技術, 1994(4): 16-20.

[10] 沈亨業, 樊光華. 淺析我國直升機技術發展問題[J]. 直升機技術, 1998(1): 46-51.

[11] 張呈林, 張曉谷, 郭士龍, 等. 直升機部件設計[M]. 南京: 航空專業教材編審組, 1986.

聲 明

本刊已加入“中國核心期刊(遴選)數據庫收錄期刊”、“中國學術期刊(光盤版)收錄期刊”、“萬方數據—數字化期刊入網期刊”和“超星期刊域出版平臺”，本刊已許可上述電子雜志社在其網站及其系列數據庫產品中以數字化方式復制、匯編、發行、信息網絡傳播本刊全文。任何稿件在本刊刊出，即表明該文章所有作者都已認可其版權至本刊編輯部，著作權使用費與本刊稿費一并支付，本刊與國內外文獻數據庫或檢索系統進行合作交流時，不再征詢作者意見。作者如有異議，須提前向本刊聲明。

《直升機技術》編輯部

Analysis of Torsional Stiffness Properties of Rotor Flexbeam

ZHANG Wangliang1, SHI Weixing2

(1.AVICOPTER CO., LTD，Tianjin 300308， China；2.NORINCO GROUPNorth Information Control Group CO., Ltd. Beijing 100089，China)

A rotor flexbeam is a core component of a bearingless rotor. Different from the conventional cantilever structure, a rotor flexbeam needs bear huge centrifugal force, while meeting the different stiffness, requirements of the flapping, the lagging and the pitching. Because there is no actual variable pitch hinge in the flexbeam structure, the variable pitch control of the rotor depends on the large deflection of the flexbeam structure. The characteristics of the fiber composites that can be tailored just meet the requirements. In this paper, some flexbeam torsion stiffness was analyzed and calculated, eight kinds of special interface torsion stiffness were analyzed. The torsion of composite materials was compared with metal material stiffness. The conclusion could provide reference for engineering design of torsional stiffness of flexbeam.

flexbeam；torsional stiffness；multi section；composite hub

2016-10-24

張旺亮(1983-)，男，江西景德鎮人，大學，工程師，主要研究方向：項目管理。

1673-1220(2017)01-031-05

V214.1+1

A