旋翼槳葉載荷與槳葉結構參數相關性研究

胡 偶，陳平劍

(中國直升機設計研究所，江西 景德鎮 333001)

旋翼槳葉載荷與槳葉結構參數相關性研究

胡 偶，陳平劍

(中國直升機設計研究所，江西 景德鎮 333001)

基于CAMRAD II軟件，建立自由尾跡耦合柔性多體動力學的彈性槳葉結構載荷分析模型，針對某直升機旋翼槳葉結構設計與載荷分析問題，開展槳葉結構參數與槳葉載荷水平的相關性研究。通過典型飛行狀態，包括超扭狀態和大前進比前飛狀態，研究槳葉剖面揮舞剛度、擺振剛度、扭轉剛度等參數的變化對槳葉揮舞與擺振方向載荷水平的影響，并分析由結構共振引起的槳葉載荷突增現象。

載荷；結構參數；共振；旋翼槳葉

0 引言

直升機旋翼槳葉載荷分析是旋翼氣動設計與結構設計的重要支撐，是旋翼系統方案設計與工程詳細設計階段旋翼槳葉強度與壽命評估的重要依據。旋翼槳葉載荷分析是典型的氣動/結構耦合問題，且是一種綜合性的系統工作：首先需建立直升機模型、旋翼和尾槳模型以及槳轂-操縱系統模型(包括各種鉸結構、變距拉桿等)，再將模型通過各種連接形式連接，然后基于氣動模型(如升力線方法)和多體動力學模型，開展旋翼槳葉載荷分析。載荷分析工作在旋翼系統設計過程中起著承上啟下的重要作用，是結構設計、載荷分析、壽命評估這一設計流程必不可少的關鍵環節。

旋翼槳葉振動載荷評估是直升機空氣動力學與動力學領域面臨的難點。受限于復雜的氣流環境、非線性結構彈性變形等耦合因素，采用數值分析方法很難獲得精確的振動載荷值。但從工程設計的角度來看，通過數值分析與解析分析方法，構建高效、準確的載荷工程計算方法，能夠滿足不同飛行狀態的載荷計算分析工作要求，形成可用于旋翼系統壽命與強度評估的載荷譜，從而有效縮短直升機旋翼系統研制周期，提高研制效率。

在國外，隨著計算技術的高速發展，形成了以CAMRAD II[1]為代表的直升機綜合氣彈分析軟件，在直升機工程設計領域得到了廣泛的應用。該軟件是由Wayne Johnson[1-2]開發的一款直升機氣動與動力學綜合分析軟件，具備多體動力學、非線性有限元以及直升機空氣動力學耦合分析能力，可用于預先研究、方案設計、詳細設計等階段直升機的性能、載荷、振動、響應及穩定性分析。CAMRAD II軟件在旋翼槳葉載荷計算方面得到了廣泛的應用驗證[3-7]，其精度能夠滿足工程設計的要求。

在國內，習娟等人[8]針對某無人直升機開展了直升機旋翼系統載荷分析技術研究，王浩文等[9]建立了旋翼系統綜合氣彈分析方法，孫韜等[10]針對典型前飛狀態開展旋翼振動載荷分析研究，吳杰等[11]比較了力積分法、反力法和曲率法三類旋翼槳葉結構載荷計算方法的預測精度和適用范圍。

本文基于CAMRAD II軟件，建立耦合自由尾跡模型和柔性多體力學思想的彈性槳葉結構載荷分析模型。選取典型飛行狀態，開展旋翼槳葉結構參數與槳葉載荷水平相關性分析，通過槳葉剖面揮舞剛度、擺振剛度、扭轉剛度等參數的變化，研究槳葉揮舞與擺振方向載荷隨槳葉結構參數的變化關系。最后，從槳葉模態分析和載荷諧波分析的角度，揭示了結構共振引起的槳葉載荷突增現象。

1 旋翼槳葉載荷計算模型

直升機旋翼槳葉載荷包括靜載和動載，計算狀態包括超轉、超扭、水平飛行、水平轉彎、螺旋轉彎、自轉下滑等狀態[8]。本文分別選取具有代表性的超扭狀態和最大速度平飛狀態開展槳葉靜載荷與動載荷分析。超扭狀態模擬的是一種極限懸停狀態，旋翼總距設為旋翼失速前的最大允許值，周期變距為零，旋翼轉速為正常轉速，該狀態考核槳葉的靜載荷的極限值。

采用CAMRAD II軟件，建立彈性槳葉載荷分析模型，主要計算流程如圖1所示。

動載荷計算過程中采用的是全機配平模型，槳葉為彈性槳葉模型，取6階模態和6階諧波，自由尾跡選取Johnson模型[4]；靜載荷采用孤立旋翼模型計算，取6階模態和0階諧波，自由尾跡選取Johnson模型[4]。

2 旋翼槳葉載荷計算結果及分析

2.1 旋翼槳葉結構參數

以某樣例直升機作為分析對象，其旋翼槳葉片數為5片，基準轉速(Ω)為258 RPM，最大平飛速度(VMAX)為260km/h。為研究槳葉結構參數對槳葉載荷的影響，首先，設計了一副基礎模型槳葉(方案 A)，圖2給出了計算得到的基礎槳葉(方案A)的固有特性。然后，在方案A槳葉的基礎上，通過調整槳葉翼型起始段之后剖面的揮舞剛度(EIFALP)、擺振剛度(EILAG)和扭轉剛度(GJ)等結構參數分布，形成如表1所示的5個備選槳葉結構方案，其中：在方案A結構參數的基礎上，(-)表示結構參數未發生明顯變化，+表示參數值提高，-表示參數值降低。

圖3展示了各方案槳葉段剖面特性參數的變化，包括槳葉剖面揮舞剛度分布與擺振剛度分布。

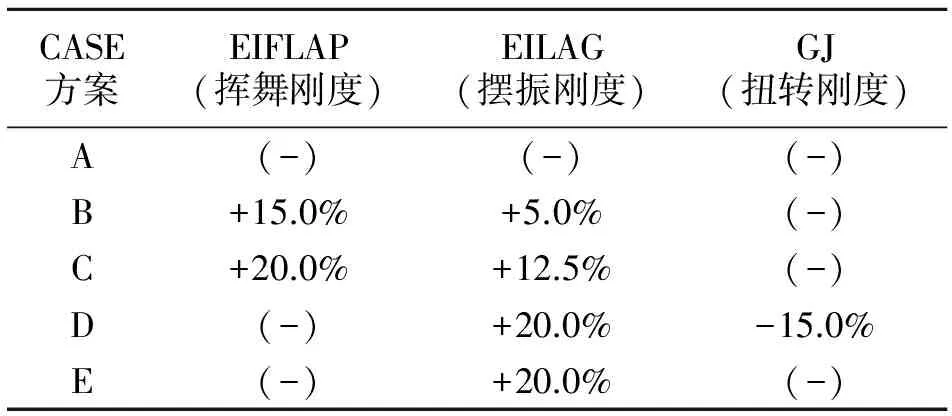
表1 槳葉剖面結構參數的變化

2.2 槳葉載荷與槳葉結構相關性分析

圖4展示了超扭狀態槳葉靜載荷與槳葉結構參數之間的關系，表2給出了槳葉0.5R剖面處的靜載荷對比。數值模擬結果表明，槳葉段的剖面揮舞彎矩主要受槳葉剖面揮舞剛度的影響，隨著揮舞剛度的增加，槳葉載荷呈線性增加趨勢，且剖面擺振剛度變化對揮舞彎矩沒有影響；在擺振方向上，槳葉剖面擺振彎矩受擺振剛度和揮舞剛度耦合影響，比較方案C與方案D可以發現，雖然方案D剖面擺振剛度比方案C高7.5%，但由于其揮舞剛度低20%，反而導致方案D的0.5R剖面擺振要小于方案C槳葉。綜上，在將葉結構設計時，必須重點考慮槳葉揮舞方向剛度的設計，因為揮舞剛度的變化能夠同時引起揮舞與擺振方向載荷的變化。

圖5展示了最大速度平飛狀態槳葉動載荷與槳葉結構參數之間的關系，表2給出了槳葉0.5R剖面處動載荷對比。數值模擬結果表明，槳葉段動載荷受結構剛度的影響較為復雜，排除方案D槳葉結構，可以發現隨著剖面揮舞剛度的增加，剖面揮舞彎矩增大；隨著剖面擺振剛度增加，擺振彎矩增大。但是方案D槳葉結構，其載荷變化不滿足這一規律，主要表現為擺振彎矩增加顯著。

2.3 結構共振引起的載荷突增現象分析

為分析方案D槳葉擺振彎矩突增的原因，對比方案D與方案E槳葉結構，兩者的差別在于扭轉剛度不一樣，方案D的扭轉剛度相比于方案E有15%的降低，因此初步確認是由于扭轉剛度變化導致載荷發生變化的。

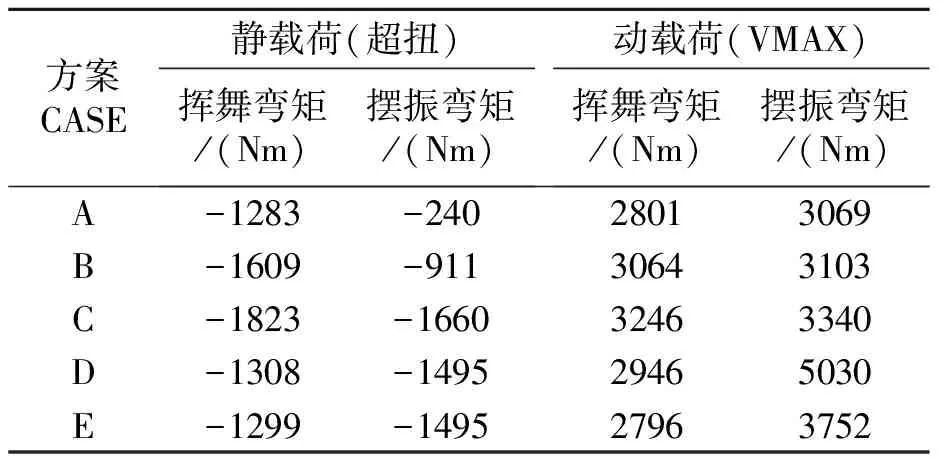
表2 不同槳葉0.5R剖面處槳葉載荷比較

首先，通過模態分析法，取最大速度平飛狀態對應的總距值，進行方案D與方案E槳葉結構的固有特性分析，得到如表3所示槳葉固有頻率特性。計算結果表明，方案D與方案E槳葉結構前3階固有頻率值一致，但該總距條件下，方案D槳葉結構的扭轉1階頻率相比于方案E槳葉更靠近6Ω。因此，從槳葉固有特性分析，導致載荷突增的原因可能是方案D槳葉6階模態與6Ω靠得近。

表3 方案D與方案E槳葉固有頻率比較

取槳葉0.5R處剖面動載荷隨方位角變化的關系，如圖6所示。揮舞彎矩方案D與方案E的載荷變化趨勢一致，而擺振彎矩則兩者有顯著的差別，方案D槳葉擺振方向載荷在周期內幅值變化劇烈。

為此，對圖6中方案D和方案E槳葉的擺振彎矩進行諧波分析[12]，獲得不同階次(Ω)下的擺振載荷幅值，如圖7所示。通過諧波分析可以看出，對于方案E槳葉結構，隨著階次的增加，擺振彎矩呈減小的趨勢，6階項稍有增大；而方案D槳葉，其擺振6階項載荷突然增加，載荷呈發散趨勢。

因而從槳葉固有頻率和載荷諧波分析兩個方面可以得出，由于存在擺振-扭轉的耦合作用，方案D槳葉結構由于扭轉剛度配置不合理，導致直升機以最大速度平飛時，出現結構共振響應，從而引起槳葉載荷高階項增加，增大了振動載荷水平。

3 結論

以某直升機旋翼為研究對象，開展了槳葉結構設計參數與載荷的相關性分析研究。基于CAMRAD II分析軟件，建立了彈性槳葉結構載荷計算方法，并針對槳葉結構設計中的關鍵參數：剖面揮舞剛度、擺振剛度和扭轉剛度的分布等，研究結構參數對槳葉揮舞彎矩與擺振彎矩的影響。研究結果表明，槳葉揮舞與擺振方向載荷主要受揮舞剛度與擺振剛度影響；由于擺振-扭轉耦合作用，當扭轉剛度布置不合理時，可能引起載荷共振響應現象的產生。通過直升機旋翼槳葉結構與槳葉載荷的相關性分析，摸清槳葉結構參數對槳葉載荷水平的影響，可為槳葉結構設計提供技術支撐，并避免可能產生的結構共振響應現象。

[1] Johnson W. CAMRAD II, Comprehensive Analytical Model of Rotorcraft Aerodynamics and Dynamics[J]. Johnson Aeronautics, 1992.

[2] Johnson W. CAMRAD II, Comprehensive Analytical Model of Rotorcraft Aerodynamics and Dynamics, Rotorcraft Applications[J]. Johnson Aeronautics, 1993.

[3] Johnson, W. Rotorcraft aerodynamics models for a comprehensive analysis[C].Presented at the 54th Annual Forum of the AHS, Washington, DC, May 20-22, 1998.

[4] Johnson, W. A General Free Wake Geometry Calculation for Wings and Rotors[C]. American Helicopter Society 51st Annual Forum, Ft. Worth, TX, May 1995.

[5] Nguyen K, Johnson W. Evaluation of Dynamic Stall Models with UH-60A Airloads Flight Test Data[C]. American Helicopter Society 54th Annual Forum, Washington, D.C., May 1998.

[6] Jones H E, Kunz D L. Comprehensive Modeling of the Apache in CAMRAD II[C]. American Helicopter Society Structure Specialists' Meeting, Williamsburg, VA,October 2001.

[7] Acree C W , Jr. A CAMRAD II Model of the V-22 for Whirl-Flutter Analysis[R]. NASA TM 2004-212801, July 2004.

[8] 習 娟，吳裕平，陳平劍. 直升機旋翼系統載荷分析技術[J].直升機技術，2007, 3: 52-54.

[9] 王浩文，高 正．采用綜合氣彈分析方法的旋翼非定常氣動載荷計算[J].南京航空航天大學學報，2003，35(3): 268-272．

[10] 孫 韜，譚劍鋒，王浩文. 典型飛行狀態下的旋翼振動載荷計算與分析[J].南京航空航天大學學報，2011,43(3): 302-307.

[11] 吳 杰，楊衛東，虞志浩. 旋翼槳葉結構載荷計算方法比較研究[J].振動與沖擊，2014, 33(7): 210-214.

[12] Johnson W. Helicopter Theory[M]. Princeton: Princeton University Press, 1980.

Correlation Study for Blade Loads and Blade Structure Properties of Rotor

HU Ou, CHEN Pingjian

(China Helicopter Research and Development Institute, Jingdezhen 333001, China)

This paper presented predictions of blade structure loads using free wake model and flexible multibody dynamics method based on the CAMRAD II software. The research was focused on the problem of structure design and predictions of blade structure loads, and the relationship of blade structure properties and structure loads was studied. Two typical flight conditions were investigated including over-torque case and high speed case. The blade section properties, such as flap bending stiffness, lag bending stiffness and torsion stiffness were changed to observe how the loads changed. Meanwhile, the resonance phenomenon of blade loads was revealed.

loads； structure properties；resonance；blade

2016-09-23

胡 偶(1984-)，男，安徽池州人，博士，工程師，主要從事旋翼系統載荷分析、計算流體力學、網格生成技術等研究。

1673-1220(2017)01-008-05

V211.52

A