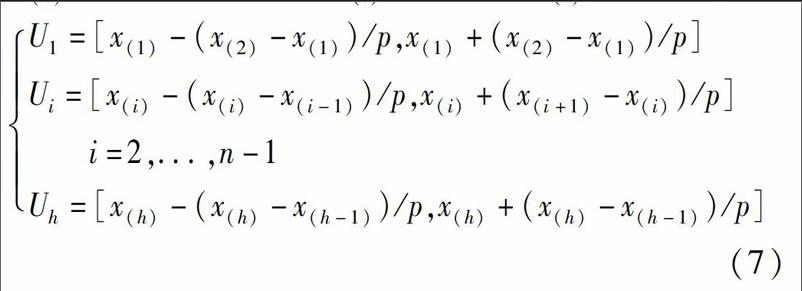小樣本情況下參數區間估計的改進方法

孫慧玲　胡偉文　劉海濤

摘要：小樣本情況下實驗數據的概率分布較難確定，傳統小樣本估計方法無法提供準確的參數估計；針對工程上常用的Bayes Bootstrap方法對小樣本可靠性參數估計僅僅是原樣本的重復，在參數區間估計上精度不夠高的問題；在不改變原樣本數據的基礎上，依據時間序列將原樣本分組并擴充，對擴充后的樣本進行參數點估計和區間估計，提出針對小樣本情況下參數區間估計的改進方法，給出了改進方法的算法。運用蒙特卡羅仿真方法進行建模仿真，結合具體算例分析，驗證新方法對小樣本情況下參數的區間估計精度有顯著提高。

關鍵詞：小樣本；Bayes Bootstrap方法；區間估計

中圖分類號：0211 文獻標志碼：A 文章編號：1007-2683（2017）01-0109-05

0 引言

樣本容量n≤30在工程上一般被認為是小樣本.如果是正態分布，小樣本的樣本量界定可能更小，甚至小于10。隨著高新技術在武器系統中的廣泛應用，武器裝備是否能保證每次成功完成任務與其可靠性直接相關，因此，可靠性是衡量裝備性能的一個重要指標；導致在研制武器裝備的過程中，其精度及可靠度要求越來越高；使得技術更復雜，造價更昂貴成為整個研制系統的大趨勢。特別是某些破壞性試驗，一次實驗往往要付出巨大的代價。針對這類試驗的傳統鑒定方法已不再適用。因為傳統鑒定方法是以經典統計理論為基礎的，也就意味著較大的樣本量必不可少，而昂貴的武器裝備從安全以及節約的方向考慮，顯然不適合進行大量試驗。

從統計學角度分析，武器裝備的可靠性研究是參數估計的范疇，是參數估計的具體實例。目前，工程上已經積累了不少方法來處理小樣本問題，根據有無先驗信息這點進行界定，它們大致可以被分為兩大類：一類是以Bayes方法為代表的傳統估計方法。該方法僅利用原始積累實驗數據也即歷史信息來估計參數。另一類是以Bootstrap和BayesBootstrap方法為代表的方法。該方法僅僅利用當前實驗數據，在樣本量較小的情況下，可以對參數進行比較準確的估計。

本文先介紹Bayes Bootstrap方法的基本思想和基本步驟；隨后分析該方法的不足之處，針對不足提出改進意見；最后通過具體算例驗證改進方法的可行性。

1 小樣本參數估計Bayes Bootstrap方法

1.1 Bayes Bootstrap方法的基本步驟

定義1 觀測樣本X=（x₁，x₂，…，x_n）為總體樣本，其樣本量是有限的，稱該樣本為原生樣本，設x_i～F（x），i=1，2，…，n，F（x）未知，則這些原生樣本構造的經驗分布函數為

（1）式中：x_（1）≤x_（2）≤…≤x_（n）是順序統計量，是按x₁，x₂，…，x_n從小到大的排序后得到的。

步驟1：假設θ=θ（F）是總體的某個參數（例如均值或方差），θ=θ（F_n）是總體參數θ的估計值，記：

1.3 Bayes Bootstrap方法的分析

根據1.1的介紹可知Bayes Bootstrap方法沒有添加任何樣本以外的信息，僅僅是在原樣本的基礎上的重復抽樣，對樣本點進行了一定的修正，并且擴大了樣本容量對原有參數進行估計。據已有的成果，小樣本情況下（樣本量為10），Bayes Boot-strap方法明顯優于經典統計法，不僅在參數點估計更接近真實值，并且得到的估計置信區間更短。

研究中發現，Bayes Bootstrap方法對Dirichlet分布和原生樣本依賴性較大。另外，Bayes Boot-strap方法的再生樣本是取自Dirichlet分布隨機數與原樣本的加權平均，在（0，1）區間生成一序列的隨機數結果有多種可能，一旦生成的隨機數均勻性不好就會導致實驗結果出現很大差別。鑒于以上局限性，有專家學者對Bayes Bootstrap方法提出了改進意見，一是對經驗函數提出改進意見，重新構造更為合理的經驗分布函數；二是對小樣本的Boot-strap抽樣方法進行改進，目的在于調整抽樣方法，增大樣本容量。在具體工程問題中，這些改進方法都有較好的適應性。

3 算例

前面介紹了小樣本參數估計的傳統方法和Bayes Bootstrap方法，本文提出了基于Bayes Boot-strap方法的改進意見并給出了仿真流程，下面通過具體實例來比較3種方法在實際問題中的適應性，驗證改進方法的優越性。

例計算機生成服從正態分布N（2，0.5）的10個隨機數1.7837，1.1672，2.0627，2.1438，1.4268，2.5955，2.5946，1.9812，2.1636，2.0873，取置信度1-α=0.95，分別用傳統小樣本估計方法、BayesBootstrap方法以及改進Bayes Bootstrap方法對參數μ作點估計和區間估計。

解：用傳統方法計算，根據式（4）可得μ的點估計μ=2.006，μ的置信度為0.95的置信區間為[1.7388，2.2625]。由于n=10是小樣本數據，考慮運用Bayes Bootstrap方法和改進Bayes Bootstrap方法對μ進行估計，方法如下：

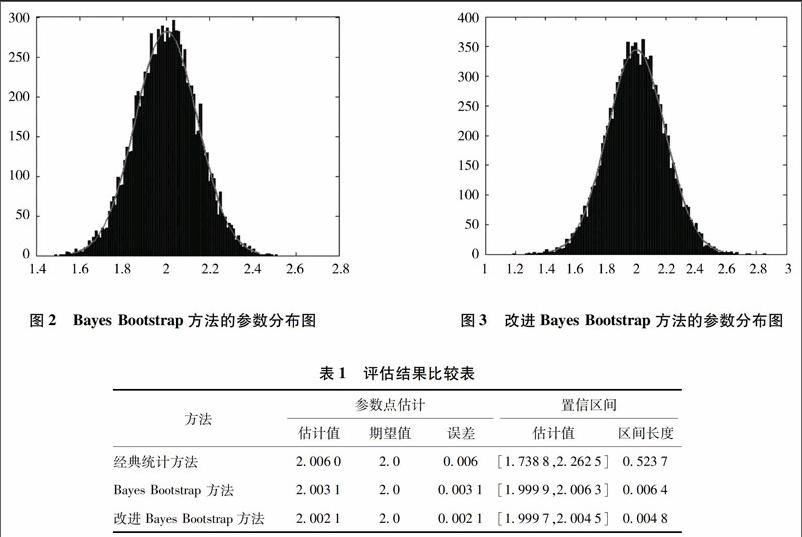
構造并產生N=10 000組自助統計量（可以更大），根據式（5）、（6），運用Bayes Bootstrap方法得到參數μ的點估計值和區間估計（見表1），μ的參數分布如圖2所示。根據改進方法增大樣本容量的思想，可將原樣本數據分為2組，運用式（8）、（9），改進Bayes Bootstrap方法得到μ的估計值和區間估計（見表1），μ的參數分布如圖3所示。

4 改進方法的評價

鑒于原Bayes Bootstrap方法對原始數據及Dirichlet分布的依賴性較大，在樣本量較小情況下很難得到滿意的估計，改進方法在以下方面克服了原方法的不足：第一，先將樣本按時間序列分組，在每一組中重構順序統計量，克服了Bayes Bootstrap方法中再生樣本數據向中間點集中的趨勢；第二，調整了抽樣方法從而擴展了樣本容量，將每一組的樣本容量都進行了擴充，并且將最大最小順序統計量延拓至非觀測點，極大地降低了再生樣本與原樣本的相似性。

5 結論

表1的數據顯示，改進方法對參數μ的點估計與原方法相差不大。而在相同置信度的情況下對參數μ的區間估計精度明顯比Bayes Bootstrap方法更好，原因是改進方法對樣本的延拓必然增大了樣本信息，從理論上講，在置信度一定的情況下，提高區間估計精度只能依靠增加樣本容量，所以，改進方法的實際建模效果與統計學原理也是一致的。

本文并未對參數σ進行估計，那么，改進方法對參數σ是否也具有良好的適應性還有待進一步研究。

（編輯：溫澤宇）