并聯系統下屏蔽數據新模型的統計分析

徐曉嶺，王蓉華，顧蓓青

(1.上海對外經貿大學統計與信息學院，上海 201620； 2.上海師范大學 數理學院，上海 200234)

【基礎理論與應用研究】

并聯系統下屏蔽數據新模型的統計分析

徐曉嶺1，王蓉華2，顧蓓青1

(1.上海對外經貿大學統計與信息學院，上海 201620； 2.上海師范大學 數理學院，上海 200234)

給出了并聯系統下屏蔽數據新模型，修正了原有的基本假定，在此基礎上推導了相應的似然函數，在全樣本、定時截尾樣本場合下研究了參數的極大似然估計，并通過Monte-Carlo模擬算例驗證方法的可行性。

并聯系統；屏蔽數據；似然函數；極大似然估計

在可靠性分析中，人們往往通過分析系統的壽命數據來估計該系統中各組成單元壽命分布中的未知參數。系統壽命試驗數據包括兩個方面，一是失效時間，二是失效原因。理想狀態下，系統的壽命數據應該包括系統失效的具體時間以及由哪個單元失效導致整個系統失效的信息。但大多數時候，導致系統失效的那個單元并不能夠被準確識別出來，人們僅能夠把導致系統失效的原因歸結為某些單元所組成的一個集合，系統真正失效的原因被屏蔽掉了。在現實生活中，由于故障診斷和故障檢測所需的費用昂貴，特別是在現代系統中越來越多地采用模塊化設計，引起系統失效的確切單元通常都是未知的。在計算機或集成電路等進行系統可靠性研究時，也會遇到相類似的屏蔽問題。導致屏蔽發生的原因很多，如：經費的不足、時間的限制、記錄的錯誤，診斷工具的缺乏及由某些單元失效所帶來的一些破壞性的后果等。這使得屏蔽數據的統計分析成為近年來研究的熱點問題之一，許多學者做了很好的工作，并取得了一系列的研究成果，在此不一一列舉。值得指出的是國際上屏蔽數據參數的估計問題最早是由Usher和Hodgson于1988年在文獻[1]中首次提出來的，在給出幾個基本假定基礎上研究其統計分析方法，其中最為關鍵的假定可表述為“屏蔽的發生與失效原因及時間無關(即獨立)”，也有學者稱為對稱性假定。在此以后的眾多研究成果無論是串聯系統、并聯系統還是混聯系統都是建立在這一基礎之上的。就并聯系統屏蔽數據的統計分析而言，國外的文獻見[2-6]，國內的文獻見[7-11]。

本文給出了并聯系統下屏蔽數據新模型，修正了原有的基本假定，在此基礎上推導了相應的似然函數，在全樣本、定時截尾樣本場合下研究了參數的極大似然估計，通過Monte-Carlo模擬算例說明方法的可行性。

1 并聯系統下屏蔽數據新模型的基本假定

基本假定1：系統由J(≥1)個獨立單元并聯而成。

基本假定2：將n個同樣的系統進行壽命試驗，試驗持續到時間τ為止，此時共有r個系統失效。(即所謂的定時截尾壽命試驗)

基本假定3：屏蔽的發生與失效原因及時間相關，當屏蔽發生時，其對應的失效原因單元(即造成系統失效的單元)被屏蔽的概率(簡稱屏蔽概率)為該單元在此時的可靠度，而與失效單元集中的其他單元無關。

值得指出的是以前文獻中的基本假定3表述為“屏蔽的發生與失效原因及時間無關(即獨立)”，其即為通常所言的對稱性假定，失效原因是指明確由于具體某個單元失效而導致系統失效。該假定即指所有單元的屏蔽概率相同。但這與實際情況很不一致。因為針對并聯通常來說可靠性高的單元其失效概率自然會比較小，被屏蔽的失效原因是可靠性高的單元的概率相對也比較高。在此假定屏蔽概率是該單元此時的可靠度，可靠性越高，失效概率越小，其屏蔽概率也越大。這比較符合實際情況。

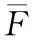
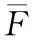
2 并聯系統下屏蔽數據新模型的似然函數

考慮n個并聯系統進行壽命試驗，每一個系統有J個單元。記Tij表示第i個系統的第j個單元的壽命，是一隨機變量。其觀察值記為tij，i=1,2,…,n,j=1,2,…,J.于是可得到第i個系統的壽命Ti為：Ti=max(Ti1,Ti2,…,TiJ)，其觀察值記為ti,i=1,2,…,n。記Si為引起系統i失效的單元集合，si為Si的實現。于是，觀察的數據data包括(t1,s1),(t2,s2),…,(tn,sn).如果集合si只含有一個元素或由單個元素組成，則表明引起系統i失效的單元是確知的。如果集合si中的元素不只一個，則說明引起系統i失效的單元壽命數據被屏蔽掉了。

就系統i而言，分兩種情形，情形一：si中的元素只有一個；情形二：si中的元素不只一個。

情形一：si中的元素只有一個

P(ti≤Ti≤ti+dti,Ki=j)

而P(ti≤Ti≤ti+dti,Ki=j)表示系統i的第j個單元在時刻ti失效，其他J-1個單元(除第j個單元)的壽命小于ti，即

P(ti≤Ti≤ti+dti,Ki=j)=

情形二：si中的元素不只一個，此時，系統i發生了屏蔽。

P(ti≤Ti≤ti+dti,Si=si)=

P(Si=si|ti≤Ti≤ti+dti,Ki=j)

而當j?si時，

P(Si=si|ti≤Ti≤ti+dti,Ki=j)=0

由此：

P(ti≤Ti≤ti+dti,Si=si)=

P(Si=si|ti≤Ti≤ti+dti,Ki=j)

當j∈si，稱P(Si=si|ti≤Ti≤ti+dti,Ki=j)為系統i在失效時刻ti時失效原因單元j被屏蔽的概率，簡稱屏蔽概率。

注意到，屏蔽概率還可寫為：

P(Si=si|ti≤Ti≤ti+dti,Ki=j)=

考慮到系統i屏蔽發生，其觀察數據為(ti,si),j∈si，于是可以認為有：

P(Si=si|ti≤Ti≤ti+dti,Ki=j)+

而P(ti≤Ti≤ti+dti,Ki=j)表示系統i的第j個單元在時刻ti失效，其他J-1個單元(除第j個單元)的壽命小于ti，即：

P(ti≤Ti≤ti+dti,Ki=j)=

當j∈si且si中的元素不只一個時，即有屏蔽發生的情形下，由假定3′知：當屏蔽發生時，其對應的失效單元的屏蔽概率為該單元在此時的可靠度，而與失效單元集中的其他單元無關。于是有

P(Si=si|ti≤Ti≤ti+dti,Ki=j)=

綜上

P(ti≤Ti≤ti+dti,Si=si)=

P(Si=si|ti≤Ti≤ti+dti,Ki=j)=

1) 全樣本場合下的似然函數

假設將n個并聯系統進行壽命試驗，不妨設在觀察的數據(t1,s1),(t2,s2),…,(tn,sn)中，前k個系統沒有屏蔽發生，即si,i=1,2,…,k中的元素只有一個，而后n-k個系統有屏蔽發生，即si,i=1,2,…,k中的元素不只一個。于是似然函數為

2) 定時截尾場合下的似然函數

如果系統由兩個單元并聯而成，即J=2。失效的原因可歸結為三類：s1={1}，s2={2}，s12={1,2}。現考慮將n個由兩個單元并聯而成的系統進行定時截尾壽命試驗，試驗持續到時間τ為止，此時共有r個系統失效。在這r個失效系統中，屬s1類的有r1個，其失效時間不妨設為t1,t2,…,tr1；屬s2類的有r2個，其失效時間不妨設為tr1+1,tr1+2,…,tr1+r2；屬s12類的有r3個，其失效時間不妨設為tr1+r2+1,tr1+r2+2,…,tr。其中r1+r2+r3=r。于是該n個并聯系統在定時截尾壽命試驗下的似然函數為

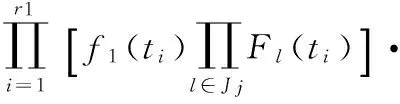
特別地，當系統進行定數截尾壽命試驗時，定數截尾數為r，此時似然函數為

3 并聯系統下屏蔽數據新模型的統計分析

1) 全樣本場合下的統計分析

如果系統由兩個單元并聯而成，即J=2。失效的原因可歸結為三類：s1={1}，s2={2}，s12={1,2}。現考慮全部失效時，屬s1類的有r1個，其失效時間不妨設為t1,t2,…,tr1；屬s2類的有r2個，其失效時間不妨設為tr1+1,tr1+2,…,tr1+r2；屬s12類的有r3個，其失效時間不妨設為tr1+r2+1,tr1+r2+2,…,tn。其中r1+r2+r3=n。于是該n個并聯系統在壽命試驗下的似然函數為

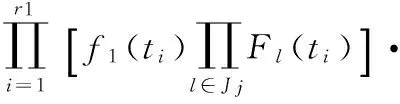
設單元1的壽命為X，其失效率為常數α1，單元2的壽命為Y，其失效率為常數α2，X,Y相互獨立，并聯系統的壽命記為T，T=max(X,Y)。

似然函數為：

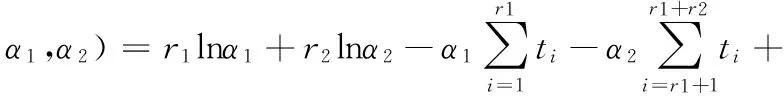
特別地，當兩個單元的失效率為相同參數時，即α1=α2=α，此時，似然函數為：

引理1：對ti,i=1,2,…,n,α>0，α的方程g(α)=0有唯一正實根。

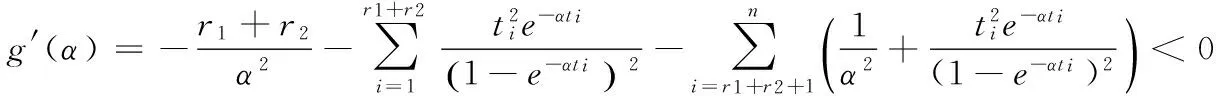
例1：取樣本容量n=10,r1=3,r2=4，失效率都取為α=0.5α=0.5，通過Monte Carlo模擬產生如表1所示的隨機數。

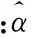
2) 定時截尾下的統計分析

如果系統由兩個單元并聯而成，即J=2。失效的原因可歸結為3類：s1={1}，s2={2}，s12={1,2}。現考慮將n個由兩個單元并聯而成的系統進行定時截尾壽命試驗，試驗持續到時間τ為止，此時共有r個系統失效。在這r個失效系統中，屬s1類的有r1個，其失效時間不妨設為t1,t2,…,tr1；屬s2類的有r2個，其失效時間不妨設為tr1+1,tr1+2,…,tr1+r2；屬s12類的有r3個，其失效時間不妨設為tr1+r2+1,tr1+r2+2,…,tr。其中r1+r2+r3=r。

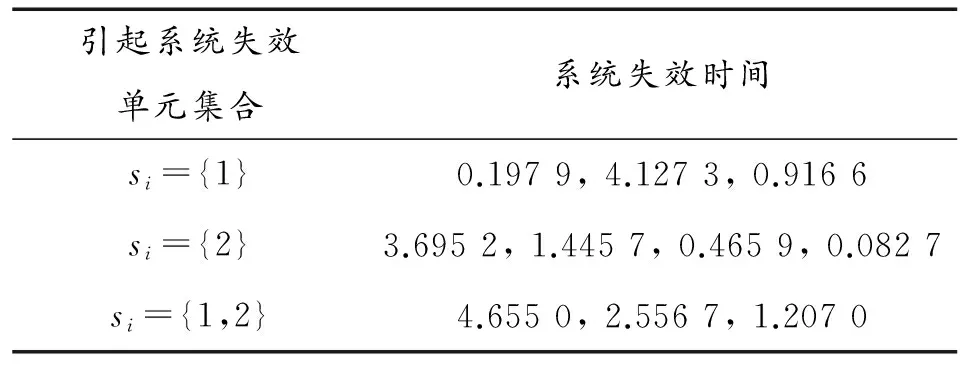
表1 n=10,r1=3,r2=4,α=0.5的隨機數

設單元1的壽命為X，其失效率為常數α1，單元2的壽命為Y，其失效率為常數α2，X,Y相互獨立，并聯系統的壽命記為T，T=max(X,Y)。對t≥0，

似然函數為：

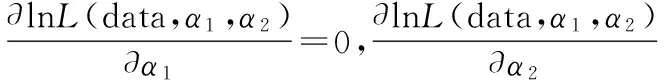
特別地，當兩個單元的失效率同為參數時，即α1=α2=α，此時，似然函數為：

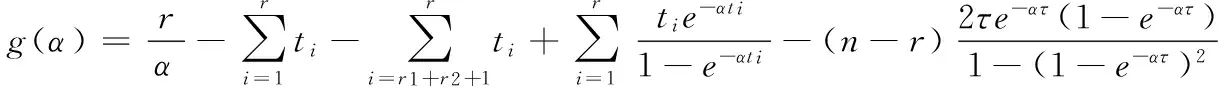
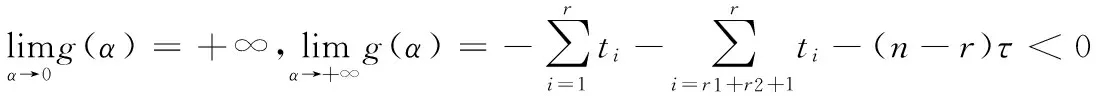
例2：取樣本容量n=20,r=18,r1=7,r2=7，兩個單元的失效率都取為α=0.01，通過Monte-Carlo模擬如表2所示的隨機數。

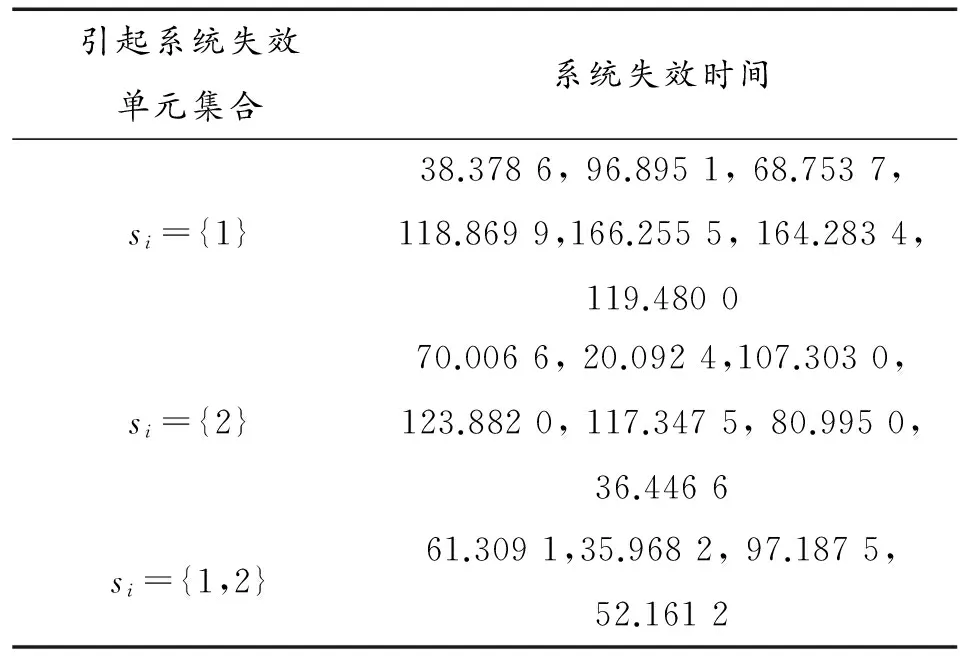
表2 n=20,r=18,r1=7,r2=7,α=0.01的隨機數

取τ=166.255 5，利用本文方法可得參數α的極大似然估計為：α=0.013 1。

例3：取樣本容量n=20,r=18,r1=6,r2=8，兩個單元的失效率分別取為α1=1,α2=1.5，通過Monte-Carlo模擬如表3所示的隨機數。

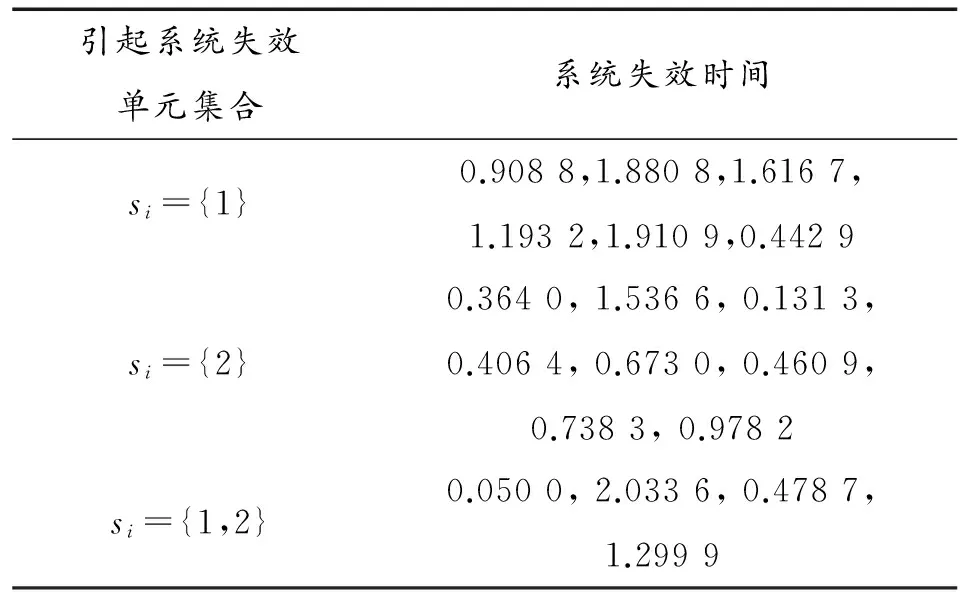
表3 n=20,r=18,r1=5,r2=10,α1=1,α2=1.5的隨機數

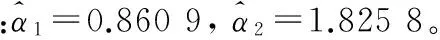
[1]JOHNS,USHER,THOMJ.HODGSON.MaximumLikelihoodAnalysisofComponentReliabilityUsingMaskedSystemLife-TestData[J].IEEETransactionsonReliability,1988,37(5):550.555.

[2]REISERB,GUTTMANI,DENNISK,etal.Usher-BayesianInferenceforMaskedSystemLifetimeData[J].Appl.Statist.,1995,44(1):79-90.

[3]AMMARM.SARHAN,AHMEDH.El.Bassiouny.EstimationofComponentsReliabilityinaParallelSystemUsingMaskedSystemLifeData[J].AppliedMathematicsandComputation,2003,138:61-75.

[4]DONALDEHUTTO,THOMASMAZZUCHI,SHAHRAMSARKANI.Analysisofreliabilityusingmaskedsystemlifedata[J].InternationalJournalofQuality&ReliabilityManagement,2009,26(7):723-739.

[5]WANGRonghua,XUXiaoling,GUBeiqing.TheStatisticalAnalysisofParallelSystemforType-ICensoredTestUsingMaskedData[C]//RecentAdvanceinStatisticsApplicationandRelatedAreas.2ndConferenceoftheInternationalInstituteofAppliedStatisticsStudies.Qingdao,CHINA,2009:789-795.

[6]XUAncha,TANGYincai.AnOverviewonStatisticalAnalysisforMaskedSystemLifetimeData[J].ChineseJournalofAppliedProbabilityandStatistics,2012,28(4):380-388.

[7] 張士峰,鄧愛民.含有屏蔽壽命數據的貝葉斯可靠性分析[J].戰術導彈技術，2001(3):34-39.

[8] 張帆,師義民.基于屏蔽數據的航空電源系統可靠性分析[J].航天控制，2009,27(4):96=100.

[9] 劉英,師義民.屏蔽數據下航天器電源系統的可靠性的統計分析[J].航天控制，2010,28(2):70-74.

[10]劉英,師義民,王婷婷.基于屏蔽數據的部件可靠性指標的貝葉斯估計[J].數理統計與管理，2010,29(5):853-860.

[11]張萌,師義民,楊揚.屏蔽數據下并聯系統廣義指數部件的可靠性估計[J].信息與控制，2011,40(4):483-496.

(責任編輯 楊繼森)

Statistical Analysis of New Model for Masked Data Under Parallel System

XU Xiao-ling1, WANG Rong-hua2, GU Bei-qing1

(1.School of Statistics and Information, Shanghai University of International Business and Economics, Shanghai 201620, China; 2.Mathematics and Science College, Shanghai Normal University, Shanghai 200234, China)

The new model of masked data was proposed for parallel system, which modifies original basic assumption. The corresponding likelihood function was derived on this basis. The maximum likelihood estimates of parameters were studied under full sample and type-II censored sample. The examples were illustrated to the feasibility of this method by Monte-Carlo simulations.

parallel system; masked data; likelihood function; maximum likelihood estimate

2016-10-28；

2016-11-30 基金項目：上海市教育委員會科研創新重點項目(14ZZ155)；上海市教育委員會科研創新一般項目(14YZ080)

徐曉嶺(1965—)，男，博士，教授，主要從事應用統計研究。

10.11809/scbgxb2017.03.037

徐曉嶺，王蓉華，顧蓓青.并聯系統下屏蔽數據新模型的統計分析[J].兵器裝備工程學報，2017(3):164-169.

format:XU Xiao-ling, WANG Rong-hua, GU Bei-qing.Statistical Analysis of New Model for Masked Data Under Parallel System[J].Journal of Ordnance Equipment Engineering,2017(3):164-169.

O213.2

A

2096-2304(2017)03-0164-06