基于樹干解析的高山松天然林單木木材生物量生長模型

魏安超，熊河先，胥 輝，李 超，閭妍宇，張 博，冷 燕，歐光龍

（西南林業大學西南地區生物多樣性保育國家林業局重點實驗室，云南 昆明 650224）

基于樹干解析的高山松天然林單木木材生物量生長模型

魏安超，熊河先，胥 輝，李 超，閭妍宇，張 博，冷 燕，歐光龍

（西南林業大學西南地區生物多樣性保育國家林業局重點實驗室，云南 昆明 650224）

以云南省香格里拉市兩塊典型樣地內的10株高山松樣木為研究對象，基于樹干解析測定和計算其單木木材生物量生長及木材生物量生長率，采用非線性混合效應模型技術，分別考慮了樣地效應和樣木效應，將所有不同隨機參數組合的模型進行擬合并分析模型的方差和協方差結構，構建其生物量生長及生物量生長率混合效應模型。結果表明：考慮樣地效應、樣木效應作為隨機效應的單水平混合效應模型和兩水平混合效應模型均提高了模型的擬合精度，其中考慮兩水平隨機效應的混合效應模型具有最佳的擬合表現，具有最低的AIC和BIC值。考慮兩水平混合效應在生物量生長量及生物量生長率模型構建中預估精度最高，分別達93.05%和89.83%；考慮樣木效應的混合效應模型次之，分別為88.34%和88.74%；考慮樣地效應的混合模型預估精度均最低，分別為83.99%和67.27%；而一般回歸模型的預估精度僅87.00%和87.11%。

木材生物量生長；生物量生長率；非線性混合效應模型；樹干解析；高山松

森林生物量是森林生態系統結構中最基本的特征之一，占全球陸地植被生物量的85%以上，是研究森林生態系統能量和物質循環的基礎［1-2］。近年來，關于森林生物量的研究中，樹干生物量在森林生物量中占有絕對的主體地位。杜虎等［1］對馬尾松、杉木、桉樹人工林生物量進行研究時發現，樹干木材生物量所占比重最大。然而，森林的生長周期長、長期定位監測比較困難等特點往往造成森林經營管理水平相對比較滯后［3］，單木生長模型的構建往往是解決這一問題的有效途徑。生長模型是以個體樹木的生長信息為基礎，模擬林分內不同年齡的樹木生長變化過程［4］。

以往建立的生物量與林齡的方程大多假定誤差是服從獨立同分布的，忽略了個體或群體之間存在的序列相關性及差異性［5］。而混合效應模型方法在一定程度上解決了以上不足，既可以反映總體的平均變化趨勢，又可以提供數據方差、協方差等多種信息來反映個體之間的差異［6］，被大量應用到林業研究中。陳東升等［7］基于Richards模型構建了不同種間落葉松林樹高生長非線性混合模型；肖銳等［8］利用兩水平混合模型對雜種落葉松樹高和胸徑生長進行了擬合；李春明［6］基于Richards變式模型和Logistic模型，利用SAS軟件進行了不同區組的杉木林（Cunninghamia lanceolata）優勢木平均高生長過程模擬；歐光龍等［9］以冪函數模型為基礎，構建了考慮區域效應的更高精度的林分生物量混合效應模型。以上研究都得到了相同結論，混合效應模型較傳統回歸模型不僅表現出更優的擬合和預估精度，而且能很好地表達數據間誤差分布情況。但是目前關于生物量生長模型構建大多為傳統理論生長模型，采用非線性混合效應模型的少有報道。與基于空間替代時間的生物量生長測定方法相比，樹干解析可以說明單株木材生物量的生長差異，準確反映單木生物量生長的差異，從而使混合效應模型可以有效地應用分析單木木材生物量由樣木效應及樣地效應引起的生長差異。

高山松（Pinus densata）是云南松與油松的天然雜交種，主要分布于我國青藏高原東南邊緣海拔2 800～3 500 m的陽坡地帶［10］。本研究選取香格里拉市小中甸和洛吉兩塊樣地作為試驗區，以高山松天然林為研究對象，基于樹干解析的方法獲得樹干生物量生長數據，分別考慮單木效應和樣地效應，采用非線性混合效應模型的方法建立高山松天然林單木木材生物量生長模型及生物量生長率模型，并對混合效應模型與傳統模型擬合結果進行檢驗比較，為模擬高山松天然林單木木材生物量的動態變化以及生物量的準確估算提供參考依據。

1 研究區概況與研究方法

1.1 研究區概況

香格里拉市位于云南省西北部，地理坐標為99°20′～100°19′E、26°52′～28°52′N。全市地形總趨勢西北高、東南低。東與四川省的稻城縣、木里縣相連，東南和南部與麗江市的玉龍縣隔江相望，西與維西縣、德欽縣以金沙江為界，北與四川省的得榮縣、鄉城縣接壤。香格里拉市東、南、西三面被金沙江環繞，是兩省七縣的結合部。植被森林覆蓋率為89%，其中針葉林占59%、闊葉林占15.6%、灌木林占18%、草地和其他作物占3.7%［11］。本研究選擇小中甸鎮（Site I）、洛吉鄉（Site II）作為研究位點（圖1）。

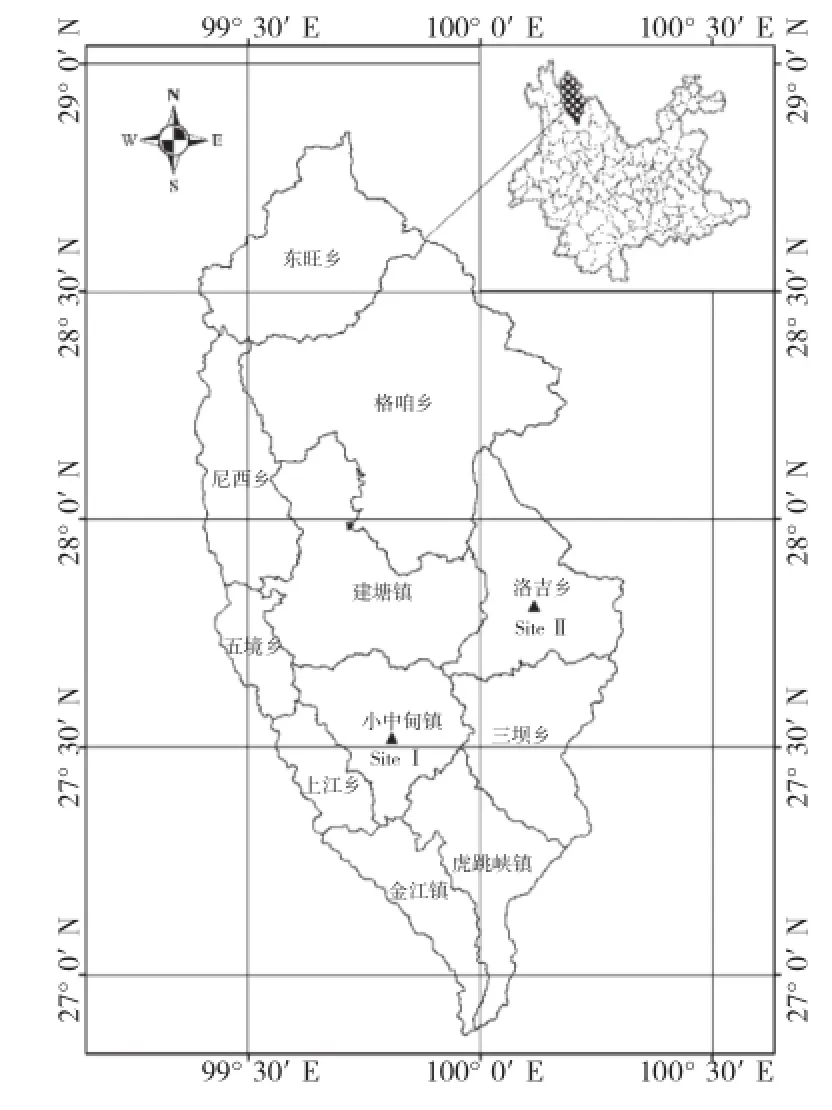
圖1 研究區位置示意

1.2 數據調查及整理

分別在香格里拉市小中甸鎮和洛吉鄉選擇一塊樣地，樣地面積為0.09 hm2。在樣地內各選擇5株樹干通直圓滿、無明顯病蟲害、梢頭完整的高山松作為樣木，編號分別為X1、X2、X3、X4、X5、L1、L2、L3、L4、L5，伐倒前準確測量基部位置、胸徑，并在樹干上標明南北方向［12］。伐倒后，從0 m處開始以2 m為區分段截取圓盤并記錄圓盤基本信息。將圓盤拋光后查數年輪，測量并記錄帶皮直徑、去皮直徑。以5年為區分年齡，測量部位圓心距后對圓盤取樣并稱量鮮重。將樣品帶回實驗室，置于105℃烘箱內烘至恒重，計算含水率，從而得到生物量。生物量生長率采用普雷斯勒式方法計算。

隨機選擇8株樣木數據，其中小中甸和洛吉各4株作為建模數據，剩余2株作為檢驗樣本，樣木基本情況見表1。

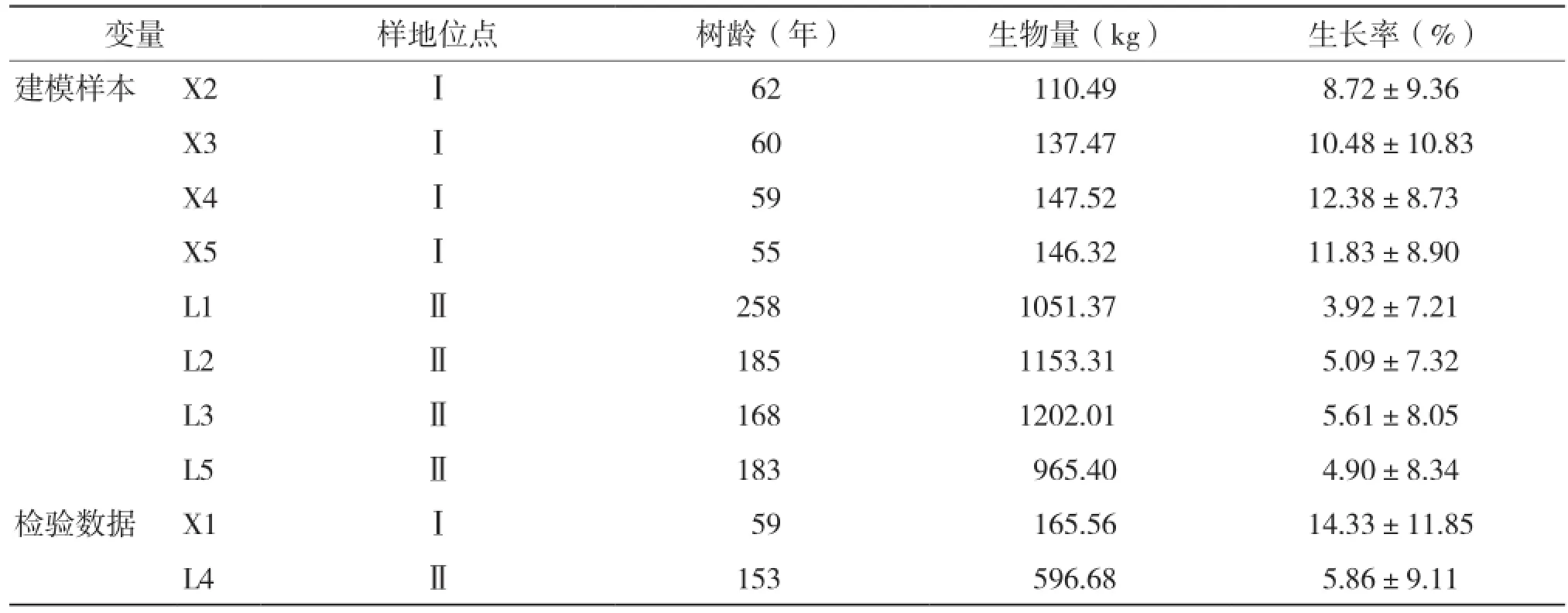
表1 樣木基本情況

1.3 數據分析

1.3.1 基本模型選型 （1）生物量生長基本模型選擇。本研究采用Logistic變式［6］作為基礎模型對生物量生長進行模擬，其模型如下：

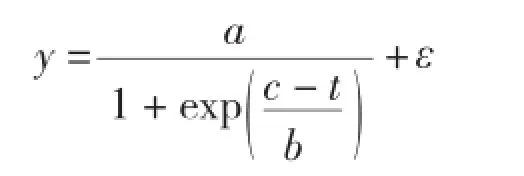
式中，y為單木木材生物量（kg）；a、b、c分別為模型中未知參數；t為樹齡；ε為誤差項。

（2）生物量生長率基本模型選擇。本研究所采用的生物量生長率與年齡的關系基本模型［13］為：

式中，y為生物量生長率；a、b為未知參數；t為樹齡；ε為誤差項。

1.3.2 混合效應模型構建 在構建混合模型之前，需要確定以下3個結構［14］：（1）混合參數選擇。在模型中，一般依賴于研究數據確定參數是固定效應還是混合效應。Pinheiro等［15］建議如果模型能收斂，首先應把模型中所有參數看成是混合參數，然后將不同隨機參數組合的模型進行擬合，利用AIC、BIC、logLik等統計量指標對模型的擬合優度進行比較，選擇模擬精度較高的形式作為最終擬合模型。

首先，我國茶染工藝在普通大眾中的認知程度較低。雖然茶及茶文化在我國具有悠久的歷史，飲茶和品茶在國人的日常生活中也比較常見，但對于茶染工藝及茶染服飾產品的關注程度就比較低。目前關于茶染工藝的研究大多集中在高校和茶文化愛好者組織，遠離普通大眾的生活，違背了藝術演變發展的邏輯。

（2）組間方差協方差結構（D）。組間方差協方差結構也被稱為隨機效應方差協方差結構，反映了組間之間的變化性，也是模型模擬中誤差的主要來源。當隨機效應參數的參數個數大于1時應考慮組間方差-協方差結構，本文以廣義正定矩陣（General Positive-Definite Matrix，Symm）考慮組間方差-協方差結構。以包括兩個隨機參數的方差協方差結構為例，其結構如下：

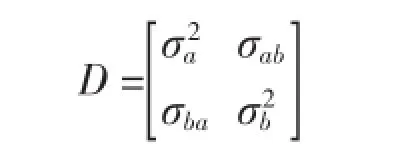
（3）組內方差協方差結構（R）。組內方差協方差結構也稱為隨機誤差效應方差協方差結構。為了確定組內的方差協方差結構，必須解決自相關結構和異方差的問題。本研究所使用的生長數據是與時間相關的，存在異方差問題，因此在模擬過程中要考慮樣地內的方差協方差結構。常用的描述R矩陣［16］的具體表達式為：

式中，Ri是樣地內方差協方差矩陣是未知的樣地i的殘差方差；Gi為描述樣地內誤差方差的異質性的對角矩陣，Гi是描述誤差效應自相關結構矩陣。

本研究采用的方差結構有冪函數（Power）和指數函數（Exp）兩種形式。協方差結構有一階自回歸矩陣〔AR（1）〕、連續一階自回歸矩陣〔CAR（1）〕、復合對稱結構〔CompSymm（）〕等3種矩陣結構作為模型的協方差結構參與模型擬合。

使用R 3.2.5軟件car模塊的nls函數和nlme模塊的nlme函數，用限制極大似然法（REML）進行建模。

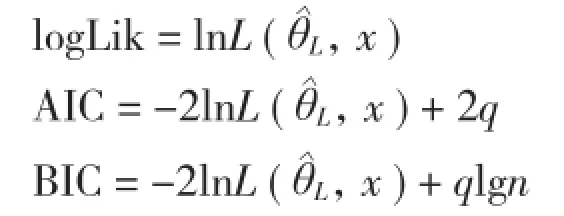
（2）獨立性樣本檢驗。模型獨立性檢驗采用建模時為使用的獨立樣本數據，對所確定模型的預測性能進行綜合評價。選取總相對誤差（Sumrelative error，SRE）、平均相對誤差（Mean relative error，MRE）、絕對平均相對誤差（Absolute mean relative error，AMRE）和預估精度（Prediction precision，PP）4個指標進行檢驗并比較評價模型的預測能力［17］。

2 結果與分析

2.1 單木生物量生長混合效應模型構建

2.1.1 基于單水平生物量生長混合效應模型構建 從表2可以看出，當考慮樣木效應時，將a、c參數作為混合參數時表現最優；僅考慮樣地效應時，將a參數作為混合參數時表現最優。

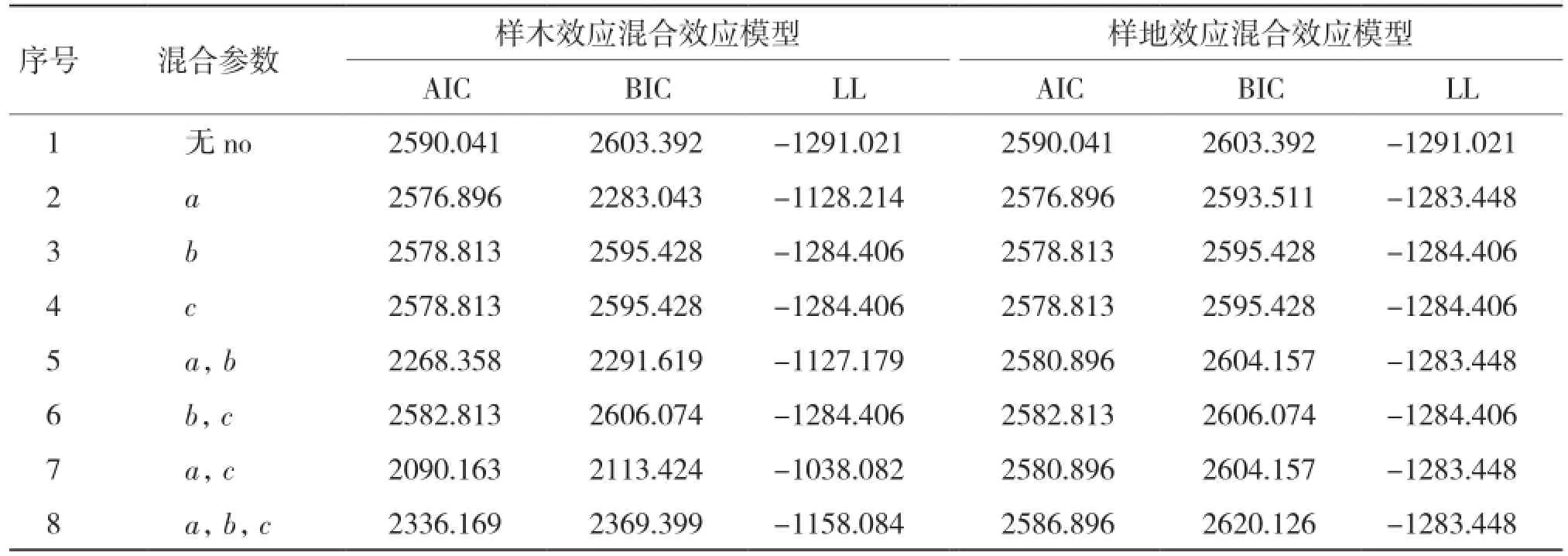
表2 生物量生長單水平混合效應模型參數比較

混合模型在參數效應確定后，還必須確定誤差的異質性和相關性。從表3可以看出，在混合效應模型中考慮方差結構時，指數函數和冪函數的方差結構均提高了模型的擬合精度，且考慮指數函數（Exp）的模型擬合精度最高；考慮3種協方差結構時，3種協方差結構均能收斂，且考慮AR（1）結構時模型提高精度最高。同時考慮方差協方差結構時，均不能收斂。

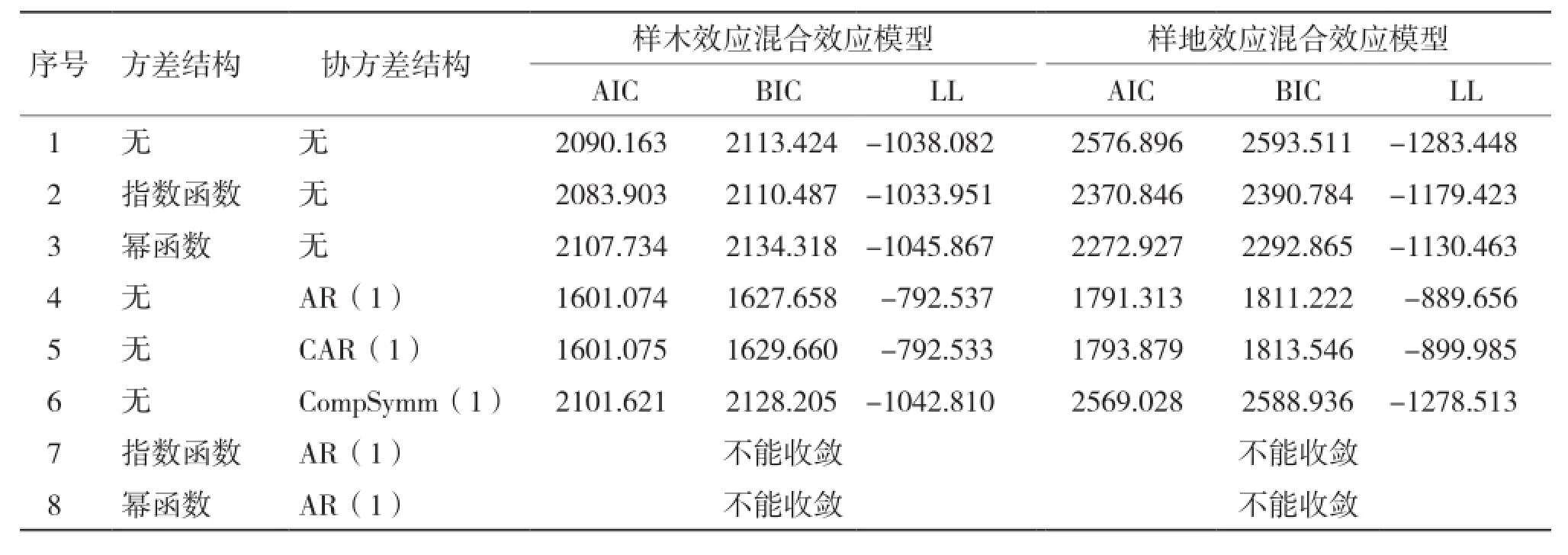
表3 考慮組內方差協方差結構的單水平混合效應模型比較

2.1.2 基于單木和樣地二水平生物量生長混合效應模型構建 能收斂的隨機效應參數組合有38種，選出7種擬合表現較好的組合列入表4。由表4可知，當樣木效應以a為混合參數，且樣地效應以b、c為混合參數時（序號2），模型表現最優，故將該模型作為基礎混合效應模型。

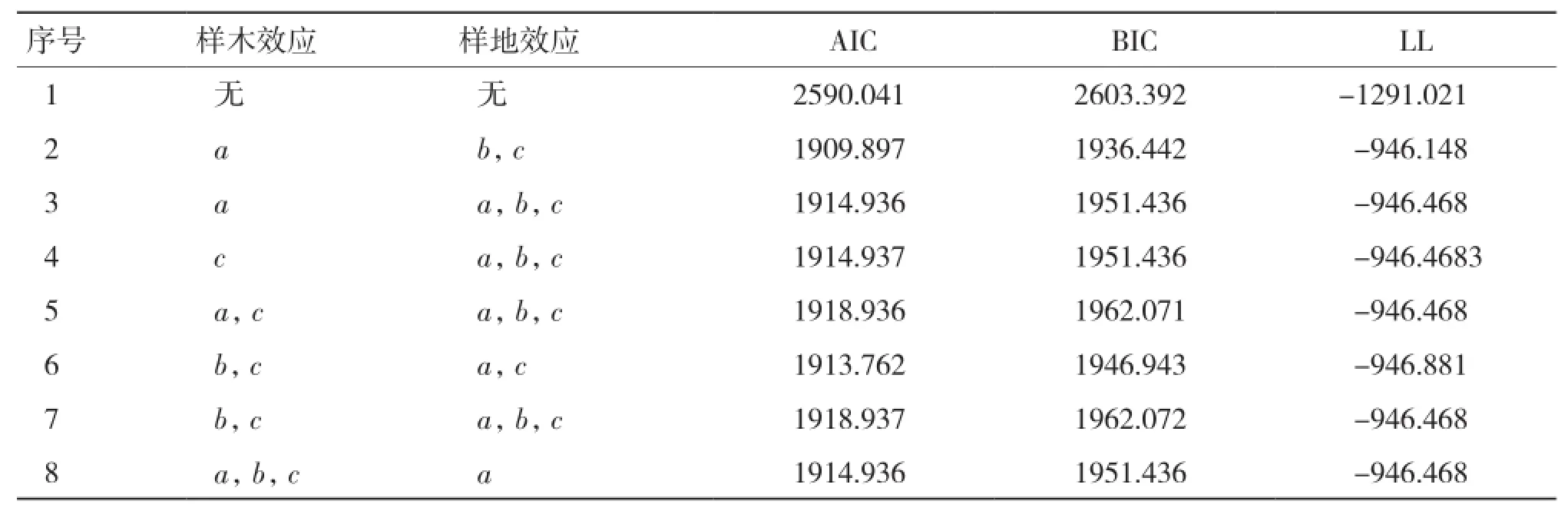
表4 兩水平生物量生長模型混合參數比較

從表5可以看出，單獨考慮冪函數和指數函數的方差結構模型擬合精度均不及原模型；考慮時間自相關序列的協方差結構均不能收斂；綜合考慮組內方差協方差結構時，模型的擬合精度比單獨考慮方差、協方差結構的精度要高，其中同時考慮冪函數方差結構（Power）和AR（1）時間自相關協方差結構時模型具有最好的擬合表現（序號7）。

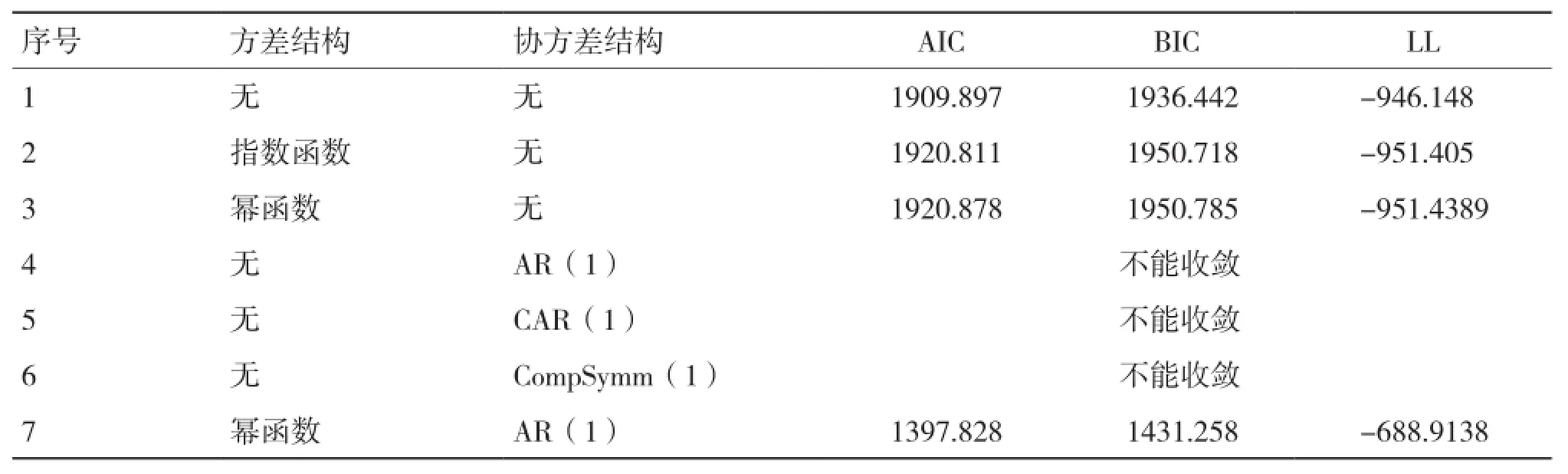
表5 不同兩水平生物生長量混合模型比較

2.2 單木生物量生長率混合效應模型構建

2.2.1 基于單水平生物量生長率混合效應模型構建 從表6可以看出，在考慮樣木效應時，將a、b參數作為混合參數時表現最優；在考慮樣地效應時，將a參數作為混合參數時表現最優。

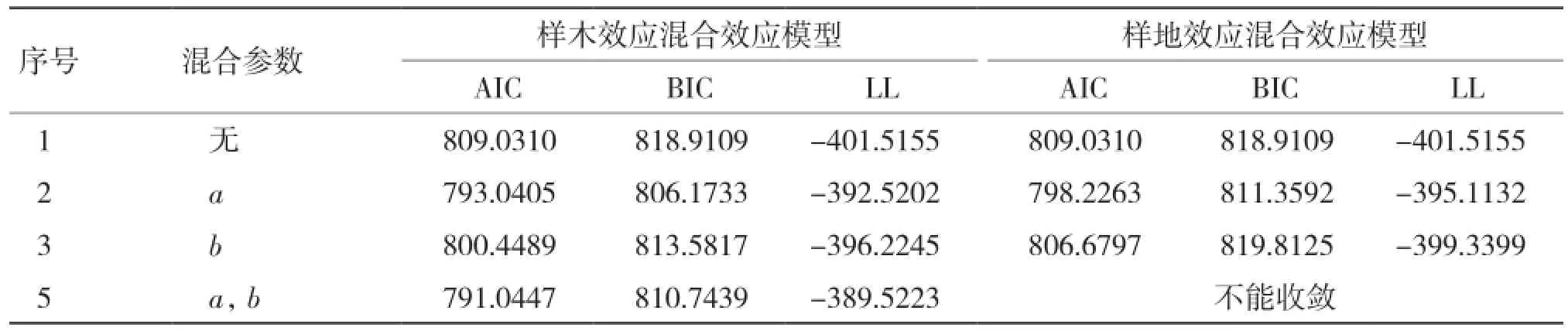
表6 生物量生長率單水平混合效應模型參數比較

由表7可知，在考慮樣木效應時，指數函數和冪函數的方差結構均提高了模型的擬合精度，且考慮冪函數（Power）的模型擬合精度最高；考慮3種協方差結構時，考慮AR（1）結構和CAR（1）時模型擬合精度相同且均能提高；綜合考慮方差協方差結構時，均不能收斂。在考慮樣地效應時，指數函數和冪函數的方差結構均提高了模型的擬合精度，且考慮冪函數（Power）的模型擬合精度最高；考慮3種協方差結構時，3種協方差結構均能收斂，其中考慮AR（1）結構和CAR（1）時模型擬合精度均能提高；綜合考慮方差協方差結構時，均能提高模型的擬合精度，其中同時考慮冪函數結構（Power）和CAR（1）模型擬合精度最優。

表7 考慮組內方差協方差結構的單水平混合效應模型比較

2.2.2 基于單木和樣地二水平生物量生長率混合效應模型構建 由表8可知，當樣木效應以a為混合參數，且樣地效應以b為混合參數時（序號3），模型表現最優，故將該模型作為基礎混合效應模型。

從表9可以看出，單獨考慮冪函數和指數函數的方差結構模型擬合精度均優于原模型；單獨考慮三種的協方差結構均不能收斂；綜合考慮組內方差協方差結構時，以同時考慮冪函數方差結構（Power）和AR（1）時間自相關協方差結構時模型具有最好的擬合表現（序號7）。

2.3 模型評價與檢驗

2.3.1 模型擬合指標分析 從表10可以看出，混合效應模型的擬合指標均優于一般回歸模型。就生物量生長量混合效應模型而言，考慮兩水平混合效應模型最好，考慮樣木效應混合模型次之，考慮樣地效應混合模型最差。就生物量生長率混合效應模型而言，考慮兩水平混合效應模型最好，考慮樣地效應混合模型次之，考慮樣木效應混合模型最差。

2.3.2 模型獨立性檢驗分析 從表11可以看出，混合效應模型中除考慮樣地效應的生物量及生物量生長率模型外，其余混合效應模型均較一般回歸模型有更高的預估精度，其中考慮兩水平混合效應在生物量生長及生物量生長率模型構建中預估精度最高，分別達93.05%和89.83%；考慮樣木效應的混合效應模型次之，分別達88.34%和88.74%；而考慮樣地效應的混合模型預估精度較低，分別是83.99%和67.27%。就生物量生長模型而言，僅考慮樣木效應時總相對誤差和平均相對誤差最小；考慮兩水平效應時，平均相對誤差絕對值最小。對于生物量生長率模型，考慮兩水平效應時，總相對誤差最小；僅考慮樣地效應時，平均相對誤差最小；一般模型的平均相對誤差絕對值最小。

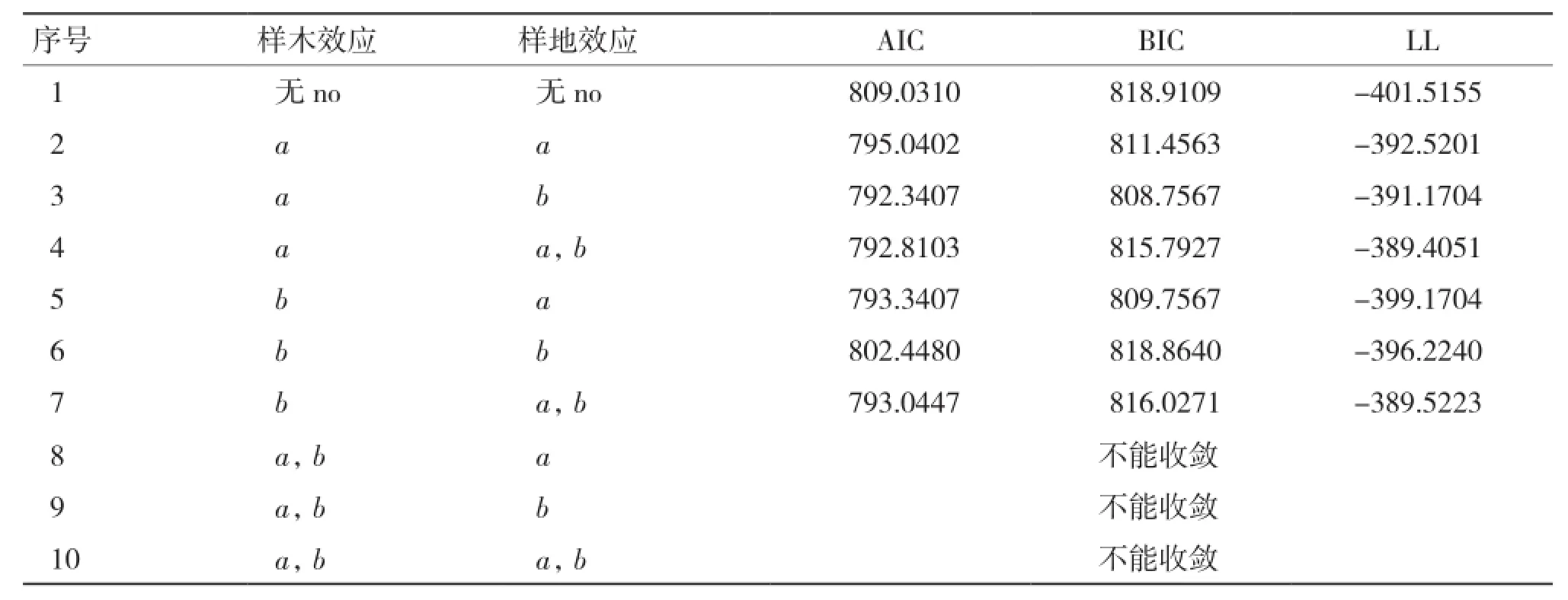
表8 兩水平生物量生長率模型混合參數比較

表9 不同兩水平生物量生長率混合模型比較

表10 模型擬合指標比較

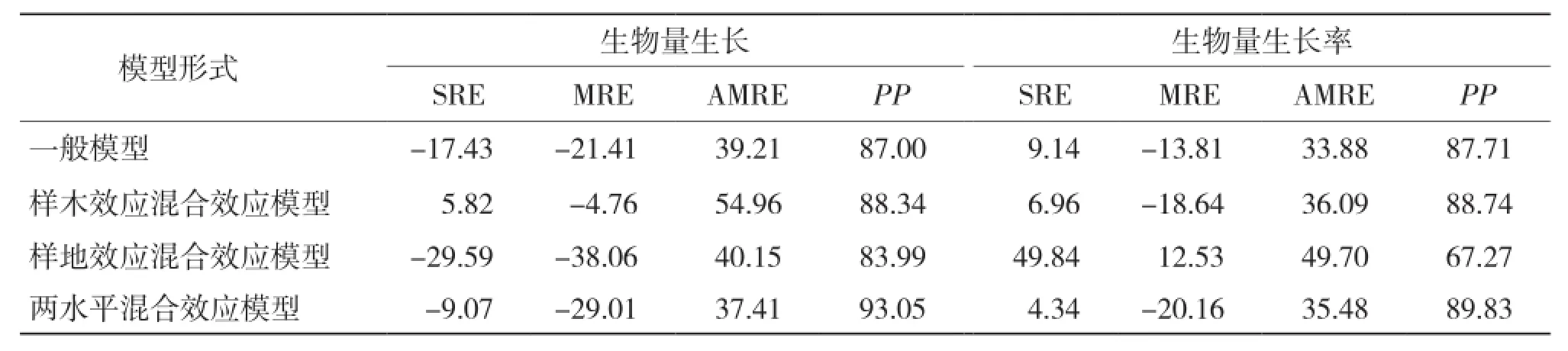
表11 生物量生長模型檢驗結果比較

2.3.3 模型擬合結果 生物量生長及生物量生長率生長模型的擬合結果分別見表12、表13。

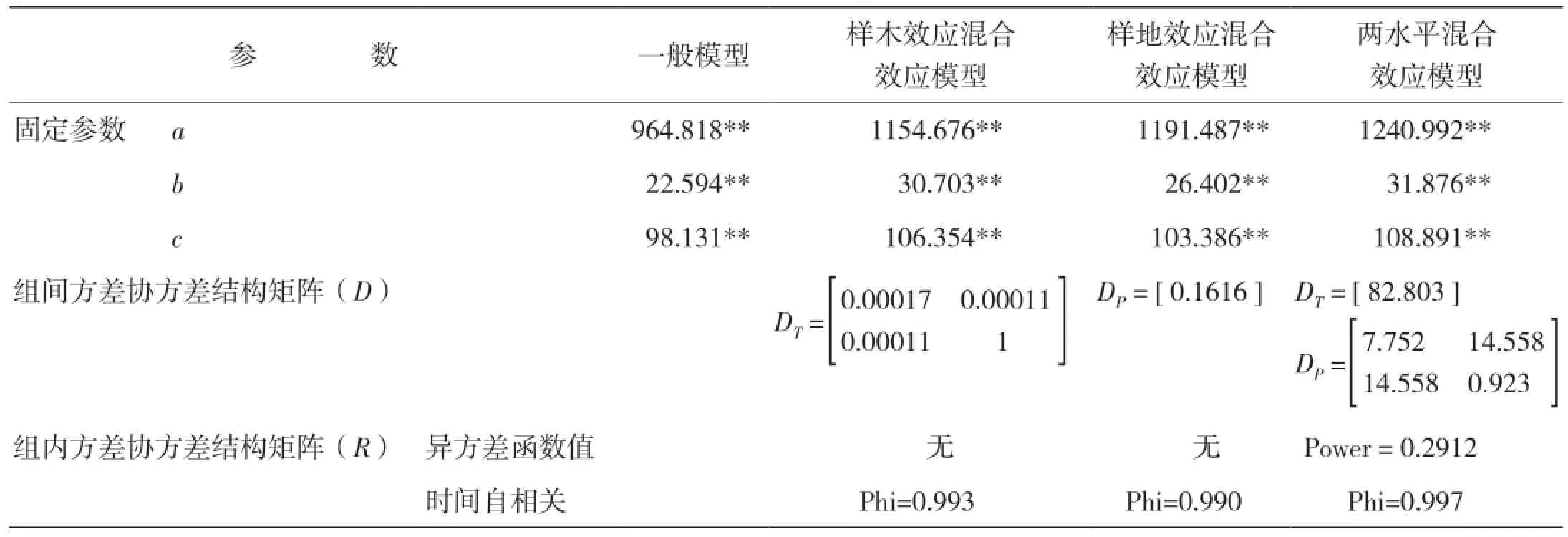
表12 生物量生長混合效應模型擬合結果

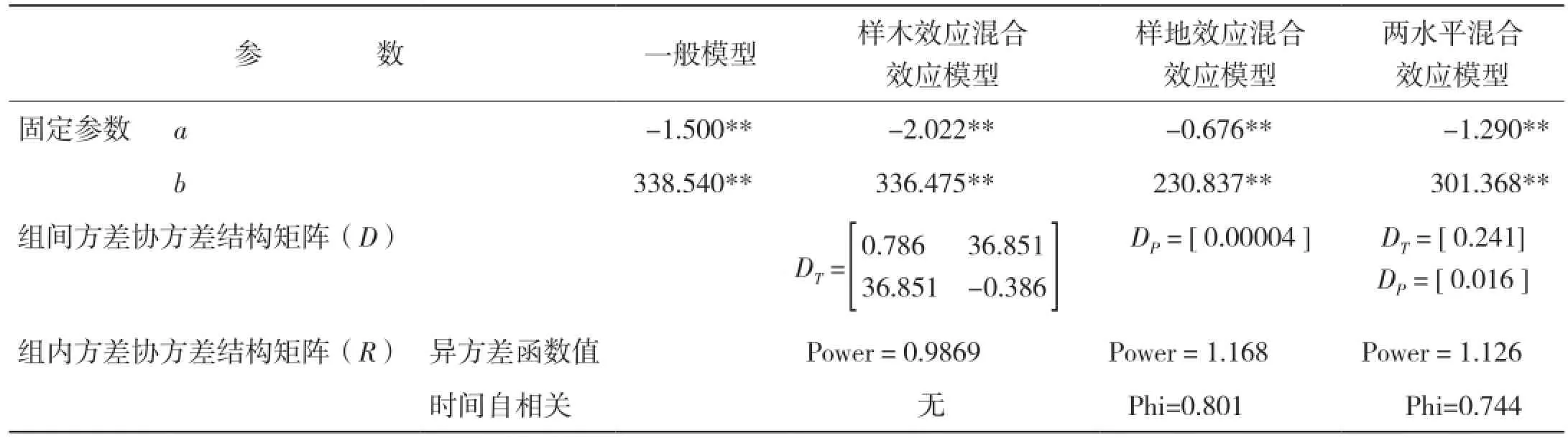
表13 生物量生長率混合效應模型擬合結果

3 結論與討論

本研究采用非線性混合模型的方法，分別建立了高山松單木木材生物量及生物量生長率與年齡關系的模型。考慮了樣地效應和樣木效應的隨機效應，將所有不同隨機參數組合的模型進行擬合。當對生物量-樹齡關系進行擬合，考慮樣木效應時，a、c同時作為混合參數模型擬合最好，由于Logistic方程中a參數表示y的上漸近值，c參數表征內稟生長率，可見，林木木材生物量生長的內稟生長率及理論最大值會隨林木個體差異而產生明顯差異；而考慮樣地效應時，a參數作為混合參數模型擬合最好，即不同立地條件的樣地會對樹木木材生物量生長的最大值產生較大影響［18］。此外，小中甸鎮樣地Ⅰ和洛吉鄉樣地Ⅱ分別為60年的成熟林和200年的過熟林，林分年齡和林木平均大小差異較大，可見林分生長狀態也是影響樹木木材生物量生長的重要因素；同時考慮樣地及樣木效應時，樣木效應以a為混合參數，樣地效應以b、c為混合參數時模型擬合最好。當對生物量生長率-年齡關系進行擬合，考慮樣木效應時，a、b同時作為混合參數模型擬合最好；考慮樣地效應時，a參數作為混合參數模型擬合最好；同時考慮樣地及樣木效應時，樣木效應以a為混合參數，樣地效應以b為混合參數時模型擬合最好。可見，非線性混合效應模型的估計精度比傳統的回歸模型精度明顯提高，但是在單木木材生物量生長及生物量生長率模型中，并非所有參數均作為混合參數的模型具有最優的擬合精度，增加隨機效應參數的個數并非會絕對增加混合效應模型的預估精度，其原因可能是由于混合參數個數的增加計算難度也隨之增加，因此模型精度反而降低［5］。

從模型擬合結果看，混合效應模型的擬合精度都比一般回歸模型的擬合精度高，且兩水平的混合效應模型具有最優的擬合表現，這與符利勇等［19］和李耀翔等［20］的結論一致。考慮樣木效應比考慮樣地效應混合效應模型的擬合精度更高，這與王春紅［21］關于紅松人工林枝條生長研究得出的結論相符，同時也說明在擬合混合效應模型時，樣地之間差異較小，誤差主要來源于不同樹木之間的差異。從模型的預估精度來看，除考慮樣地效應的單木木材生物量及生物量生長率模型外，其余混合效應模型均較一般回歸模型有更高的預估精度，其中兩水平的生物量生長及生物量生長率混合效應模型的預估精度最高，分別達到93.05%和89.83%；單獨考慮樣木效應的模型預估精度次之，分別是88.34%和88.74%；單獨考慮樣地效應的模型預估精度最低，分別是83.99%和67.27%，且低于一般回歸模型的87.00%和87.11%。可見，具有較好擬合效果的模型未必會具有更高的預估精度，這與歐光龍［22］對思茅松生物量模型擬合中的結果一致。

本研究采用的廣義正定矩陣（General Positive-Definite Matrix）結構考慮組間方差-協方差結構，而在混合效應模型中，組間方差協方差結構還有多種結構，如對角正定矩陣（Diag）、多重身份正定矩陣（Ident）、無結構（UN）、復合對稱（CS）等，這些仍需進一步深入研究。

［1］ 杜虎，曾馥平，王克林，等. 中國南方3種主要人工林生物量和生產力的動態變化［J］. 生態學報，2014，34（10）：2712-2724.

［2］ 郭兆迪，胡會峰，李品，等. 1977～2008年中國森林生物量碳匯的時空變化［J］. 中國科學：生命科學，2013（5）：421-431.

［3］ 劉平，王玉濤，楊帆. 基于單木生長模型的森林動態模擬系統研究進展［J］. 世界林業研究，2011，24（5）：25-30.

［4］ 鄧紅兵，郝占慶. 紅松單木高生長模型的研究［J］. 生態學雜志，1999（3）：19-22.

［5］ 李春明，張會儒. 利用非線性混合模型模擬杉木林優勢木平均高［J］. 林業科學，2010，46（3）：89-95.

［6］ 李春明. 混合效應模型在森林生長模型中的應用［J］. 林業科學，2009，45（4）：131-138.

［7］ 陳東升，孫曉梅，李鳳日. 基于混合模型的落葉松樹高生長模型［J］. 東北林業大學學報，2013（10）：60-64.

［8］ 肖銳，陳東升，李鳳日，等. 基于兩水平混合模型的雜種落葉松胸徑和樹高生長模擬［J］. 東北林業大學學報，2015（5）：33-37.

［9］ 歐光龍，胥輝，王俊峰，等. 思茅松天然林林分生物量混合效應模型構建［J］. 北京林業大學學報，2015（3）：101-110.

［10］ 沈志強，盧杰，華敏，等. 西藏色季拉山高山松種群點格局分析［J］. 西北農林科技大學學報（自然科學版），2016，44（5）：73-81.

［11］ 岳彩榮，唐瑤，徐天蜀，等. 香格里拉縣植被凈初級生產力遙感估算［J］. 中南林業科技大學學報，2014（7）：90-98.

［12］ 孟憲宇. 測樹學［M］. 第3版. 北京：中國林業出版社，2006.

［13］ 劉炳英，厲保志，王允壽，等. 5樹種材積生長率與年齡的關系［J］. 山東林業科技，1991（S1）：24-26.

［14］ Fang Z，Bailey R L. Nonlinear Mixed Effects Modeling for slash pine dominant height growth following intensive silvicultural treatments［J］.Forest Science，2001，47（47）：287-300.

［15］ Pinheiro J C，Bates D M. Mixed Effects Models in S and S-plus［M］. New York：Springer Verlag，2000.

［16］ Davidian M，Gallant A R. The Nonlinear Mixed Effects Model with a Smooth Random Effects Density［J］. Biometric，1993，80：475-488.

［17］ 胥輝. 一種生物量模型構建的新方法［J］. 西北農林科技大學學報（自然科學版），2001，29（3）：35-40.

［18］ 段愛國，張建國，童書振. 6種生長方程在杉木人工林林分直徑結構上的應用［J］. 林業科學研究，2003，16（4）：423-429.

［19］ 符利勇，唐守正，張會儒，等. 基于多水平非線性混合效應蒙古櫟林單木斷面積模型［J］. 林業科學研究，2015，28（1）：23-31.

［20］ 李耀翔，姜立春. 基于2層次線性混合模型的落葉松木材密度模擬［J］. 林業科學，2013，49（7）：91-98.

［21］ 王春紅. 基于非線性混合模型的紅松人工林枝條生長［J］. 應用生態學報，2013，24（7）：1945-1952..

［22］ 歐光龍. 氣候變化背景下思茅松天然林生物量模型構建［D］. 哈爾濱：東北林業大學，2014.

（責任編輯 張輝玲）

Construction of individual wood biomass growth models for Pinus densata natural forests based on stem analysis

WEI An-chao，XIONG He-xian，XU Hui，LI Chao，LYU Yan-yu，ZHANG Bo，LENG Yan，OU Guang-long

（Key Laboratory of State Forest Administration for Biodiversity Conservation in Southwest China，Southwest Forestry University，Kunming 650224，China）

Taking 10 Pinus densata sampling trees at two plots located in Shangri-La city of Yunnan province as the research object，we measured and calculated single wood biomass growth and wood biomass growth rates based on stem analysis. Considering random effect of the plot effect and tree effect，the biomass growth and growth rate models were constructed by nonlinear mixed effect model technology，and all the different random parameter combinations were fitted and the variance and covariance structures of the models were analyzed. The results showed that，considering random effect of plot effect and tree effect model as the single-level mixed effect model and two-level mixed effect model，the fitting precision of the models was improved，especially two-level mixed effect model had the best fitting performance with the lowest values for AIC and BIC. Both biomass growth and growth rates two-level mixed effect models had the highest prediction accuracy，and the values reached 93.05% and 89.83%；the secondbest ones were the mixed effect model considering the random effect of tree effect，and the prediction accuracies were 88.34% and 88.74%，respectively；the prediction accuracies of models considering the plot effect were 83.99% and 67.27%，respectively；and the prediction accuracies of ordinary models were 87.00% and 87.11%，respectively.

wood biomass growth；biomass growth rate；nonlinear mixed model；stem analysis；Pinus densata

S758.2

A

1004-874X（2017）01-0066-10

2016-10-11

國家林業公益性行業科研專項（2014040309）；西南林業大學云南省重點學科（林學）項目；國家自然科學基金（31560209）

魏安超（1991-），男，在讀碩士生，E-mail：weianchao@foxmail.com

歐光龍（1983-），男，博士，副教授，E-mail：olg2007621@126.com

魏安超，熊河先，胥輝，等. 基于樹干解析的高山松天然林單木木材生物量生長模型［J］.廣東農業科學，2017，44（1）：66-75.