螺旋非圓錐齒輪齒面節線數學模型的構建

許愛芬,賈巨民，陳雨青

(1.軍事交通學院 軍事物流系，天津 300161； 2.41軍工兵力，湖南 衡陽 421000)

?

● 基礎科學與技術 Basic Science & Technology

螺旋非圓錐齒輪齒面節線數學模型的構建

許愛芬1,賈巨民1，陳雨青2

(1.軍事交通學院 軍事物流系，天津 300161； 2.41軍工兵力，湖南 衡陽 421000)

以研究螺旋非圓錐齒輪齒面節線的構建原理為目的，基于映射法構建螺旋非圓錐齒輪齒面節線的數學模型，依據密切面的思想及算法，完成螺旋非圓錐齒輪實體模型的構建。運動學仿真結果驗證了該算法及模型的正確性。

變傳動比；非圓錐齒輪；齒面節線

汽車差速器的作用是保證汽車驅動橋兩側車輪在行程不等時能以相應的不同轉速旋轉，從而滿足汽車行駛運動學的要求。為提高車輛通過冰雪、泥濘及松軟地面的能力，限滑差速器應運而生，其結構形式可以分為人工控制式、被動控制式和主動控制式。變傳動比限滑差速器作為被動控制式的一種，近年來成為業界研究的熱點。其核心機構是一對非圓錐齒輪副，能夠實現相交軸之間的變速比傳動，既可以實現普通圓錐齒輪差速器的差速功能，也可以鎖緊防滑。

賈巨民等[1]、趙玉民等[2-3]、馬延會[4]主要對非圓錐齒輪的設計原理進行了研究。文獻[1]應用微分幾何的曲面論定理，將非圓錐齒輪副傳動的球面節曲線保測地曲率地映射到平面上，引入當量齒輪和當量節曲線的概念，將復雜的空間嚙合問題簡化成平面問題，給出齒形的設計計算方法。平面設計完成后，再采用相反程序，將平面齒形曲線保測地曲率地映射到球面上，生成空間的三維齒廓。文獻[2-4]在文獻[1]的分析方法基礎上，給出了非圓錐齒輪節曲線展開的詳細算法，并以此為基礎，通過確定插齒刀的節圓沿平面當量節曲線做純滾動時插齒刀上各點的運動軌跡，模擬插齒刀加工包絡出當量齒輪的齒形過程，并實現非圓錐齒輪的計算機輔助設計。

賈慶祥等[5]和裴玉哲[6]主要對非圓錐齒輪的加工方法進行了研究。根據短程曲線的測地曲率原理和圓錐齒輪球面漸開線形成原理，提出了一種非圓錐齒輪的球面漸開線齒廓設計方法，并在CIATA中進行三維建模及運動分析。其目的是為了產形線切齒法在非圓錐齒輪的球面漸開線齒加工方面的推廣和應用。

文獻[7-8]主要對非圓錐齒輪副進行了試驗研究。分析了一種三周節變傳動比限滑差速器的工作原理，并將其與裝有普通差速器的車輛進行性能對比試驗。試驗結果表明該差速器具有增大牽引力和縮短制動距離的作用。

鄭方炎等[9]和侯東海等[10]主要對斜齒非圓(錐)齒輪進行了研究。文獻[9]將斜齒錐齒輪的理論知識應用到非圓齒輪領域，得到了斜齒非圓錐齒輪的傳動形式，基于包絡原理的齒面生成方法，推導了其數學模型，并建立了非圓錐齒輪的模型。文獻[10]介紹了非圓齒輪齒廓的形成原理。基于工具斜齒條法加工斜齒非圓齒輪動軸線變傳動比復雜的運動幾何關系，建立了其理論分析的數學模型，分析了斜齒非圓齒輪齒廓的端面截形、節圓柱面截形以及瞬時接觸線。

上述各研究成果對本文的研究提供了極有價值的理論借鑒，但是其研究對象主要是直齒非圓錐齒輪。螺旋錐齒輪與直齒錐齒輪相比，具有重疊系數大、負載能力強、可以實現大傳動比等優點。因此，對螺旋非圓錐齒輪進行研究具有極重要的理論意義和極高的工程實用價值。

1 螺旋非圓錐齒輪齒面節線數學模型的構建

1.1 齒面節線的形成原理

本文利用螺旋圓錐齒輪的齒面節線(螺旋線)向非圓錐齒輪節面進行映射的方法求得非圓錐齒輪的齒面節線，即令螺旋圓錐齒輪與非圓錐齒輪的節面進行純滾動運動，求出螺旋圓錐齒輪的齒面節線與非圓錐齒輪節面的交點，連接成線，即可獲得非圓錐齒輪的齒面節線。

螺旋圓錐齒輪的齒面節線方程為

式中：Tb為螺旋線的螺距；γ為轉動角度；μ為圓錐錐角的一半；L為母線長。

以非圓錐齒輪的錐頂為原點建立固定坐標系O0-x0y0z0，以螺旋錐齒輪大端的圓心為原點建立固定坐標系O1-x1y1z1，當螺旋錐齒輪繞旋轉軸轉過角度θ后，其隨動坐標系為O2-x2y2z2，如圖1所示。

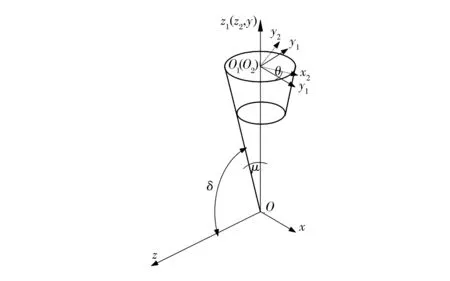
圖1 螺旋錐齒輪與非圓錐齒輪節面位置關系

1.2 螺旋非圓錐齒輪齒面節線的生成

首先將坐標系O2-x2y2z2中的點轉換到坐標系O1-x1y1z1中，根據坐標變換關系[11]，兩坐標系相差的角度為θ，因此坐標變換關系為

θ可以根據螺旋錐齒輪節面和非圓錐齒輪節面之間的純滾動關系求出[12]，母線為一定值時，節曲線的長度為

式中：

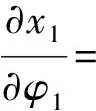
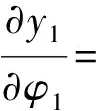
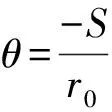
根據上述計算，便可以將坐標系O2-x2y2z2中的點轉換到坐標系O1-x1y1z1中。當球面半徑a為一定值時，利用坐標變換便可以得到坐標系O1-x1y1z1與O0-x0y0z0的變換關系。對于任意的球面半徑a，節曲線上周向的單位切向量t1為

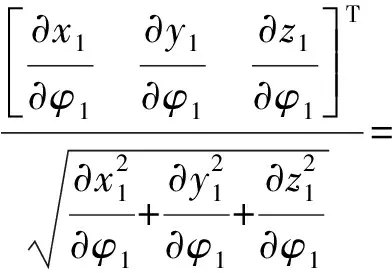
同理，徑向的單位切向量t2為

根據向量叉乘的定義，可以得到與向量t1和t2分別垂直的向量n為

n=t1×t2

由于n的方向并不與圓錐底面平行，而是相差一定的角度，因此將n偏轉一定角度，獲得新向量m，使其經過圓錐底面圓心：

m=t2sinμ+ncosμ

式中μ為螺旋錐齒輪錐角的一半。

向量m的3個方向的分量分別是m1、m2、m3。節曲線的法線等距線是根據曲線上任意一點坐標及該點沿m向量方向的位移構建的，可以表示為

(xm,ym,zm)即為坐標系O1-x1y1z1原點坐標，還需要求出這個坐標系的方向參數，再使用向量間的坐標變換。坐標系O1-x1y1z1的坐標軸用向量可以表示為

坐標系O0-x0y0z0的坐標軸向量為

根據坐標變換原理，可以得到坐標系O1-x1y1z1和坐標系O0-x0y0z0的坐標變換關系：

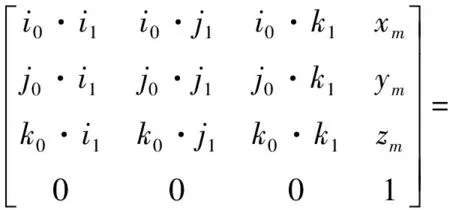
式中：p1、p2、p3為向量p的3個分量；q1、q2、q3為向量q的3個分量。

綜上所述，將圓錐面上螺旋線坐標轉換到非圓錐齒輪坐標系為

r=M10M21r0

(1)

將各個參數代入式(1)，即可將圓錐面上的螺旋線映射到非圓錐齒輪節面上，從而獲得非圓錐齒輪齒面節線的數學模型。

本課題研究的螺旋非圓錐齒輪共有9個齒，每個齒與節錐可以相交出兩條齒面節線，共18條齒面節線。將上述齒面節線的數學模型通過Matlab編程、SolidWorks環境繪制得到的齒面節線如圖2所示。

2 螺旋非圓錐齒輪模型生成

基于密切面思想，將螺旋非圓錐齒輪的齒面節線分割為若干份，每個分割點將對應一條球面節曲線，以該球面節曲線為基礎，以分割點為起點，根據文獻[1]的方法分別計算出齒形曲線，并將齒形曲線沿齒面節線方向進行放樣連接，即可獲得螺旋非圓錐齒輪的齒形(如圖3所示)。圖4為螺旋非圓錐齒輪副的嚙合圖。

圖2 齒面節線示意

(a)單周期內的齒形 (b)全周期內的齒形 圖3 螺旋非圓錐齒輪的齒形

圖4 螺旋非圓錐齒輪副的嚙合

將圖4中的齒輪副基于ADMAS環境進行運動仿真，結果表明，其運轉狀況良好，不會出現卡死、漏齒等情況，其實際嚙合曲線與理論曲線基本相符，在此不再贅述。

3 結 論

(1)本文所提出的“映射法”生成非圓錐齒輪齒面節線的方法是切實可行的；

(2)基于密切思想構建的螺旋非圓錐齒輪的模型是正確的。

上述研究成果為變傳動比限滑差速器非圓錐齒輪設計及其嚙合理論的完善及創新提供了理論和技術支撐。

[1] 賈巨民,高波,趙德龍.基于保測地曲率映射的非圓錐齒輪傳動設計分析方法[J].機械工程學報,2008,44(4):53-57.

[2] 趙玉民,倪俊義,馬延會.非圓錐齒輪的三維計算機輔助設計[J].機械傳動,2010,34(9): 47-50.

[3] 趙玉民,馬延會,華林，等.非圓錐齒輪節曲線的平面展開算法研究[J].中國機械工程,2008,19(17):2046-2049.

[4] 馬延會.變傳動比限滑差速器的齒輪設計[D].武漢:武漢理工大學,2007.

[5] 賈慶祥,裴玉哲,高士龍，等.球面漸開線齒形非圓錐齒輪的設計與分析[J].機械傳動, 2014,38(3): 80-82.

[6] 裴玉哲.球面漸開線非圓錐齒輪產形線切齒法的研究[D].長春:吉林大學,2014.

[7] 姜虹,王小椿.三周節變傳動比限滑差速器設計與試驗[J].農業機械學報,2007,38(4):31-34.

[8] 姜虹,王小椿.三周節變傳動比限滑差速器性能分析及試驗研究[J].工程機械,2006,37(12):19-22.

[9] 鄭方焱,李波,吳俊峰，等.斜齒非圓錐齒輪的數學模型與實例分析[J].機械設計, 2014,31(11):41-45.

[10] 鄭方焱,劉忠明.用工具斜齒條法加工斜齒非圓齒輪的嚙合理論模型[J].機械工程學報, 2003,39(8):49-54.

[11] 吳序堂. 齒輪嚙合原理[M].3版．北京：機械工業出版社,2009：127-131.

[12] 吳序堂,王貴海.非圓錐齒輪及非勻速比傳動[M].北京：機械工業出版社,1997：45-49.

(編輯：史海英)

Mathematical Model of Tooth Section Line of Spiral Noncircular Bevel Gear

XU Aifen1, JIA Jumin1, CHEN Yuqing2

(1.Military Logistics Department, Military Transportation University, Tianjin 300161, China; 2.41 Army Corps of Engineers, Hengyang 421000, China)

s： To study the building principle of tooth section line of spiral noncircular bevel gear, the paper firstly establishes a mathematical model of tooth section line of spiral noncircular bevel gear with mapping method, and then establishes a spiral noncircular bevel gear solid model according to the theory and algorithm of osculating planes. The Kinematics simulation results verify the correctness of the algorithm and the model.

variable ratio; noncircular bevel gear; tooth section line

2016-07-03；

2016-07-16．

天津市應用基礎與前沿技術研究計劃項目(12JCZDJC34600)．

許愛芬(1972—)，女，博士，副教授．

10．16807/j.cnki.12-1372/e.2017.03.021

TH132.42

A

1674-2192(2017)03- 0087- 04