礦用汽車轉向機構仿真與優化

太原重工股份有限公司技術中心　朱濤

一、引言

煤炭和鐵礦是支撐全球經濟發展的重要資源，其開采及運輸工作是高效開發利用礦產資源的重要環節。礦用汽車作為主要運輸工具，運輸著露天礦區40%的煤炭及90%的鐵礦，同時在大型水利工程建設行業中也有著廣闊的發展空間。礦用汽車被廣泛應用于煤、鐵、銅、鋁和油砂等各種露天礦山的運輸任務中，這些工程場所路況差、坡路較多而且環境惡劣復雜，往往是連續滿載上坡，而下坡時又必須連續制動，因此對礦用汽車的使用安全性及可靠性要求很高。同時，由于重型礦用汽車批量小，造價非常高，對道路又有一定的要求，所以無法像公路車輛一樣可以在實驗室進行零部件和整車試驗，通過試驗來評價和改進設計。因此，在礦用汽車的開發設計過程中，計算機輔助工程技術得到越來越多的應用，這對縮短開發設計周期和節約生產成本意義重大。

轉向機構作為礦用汽車的重要組成部分，用來改變或恢復其行駛方向，對行駛安全至關重要。轉向機構的設計影響著礦用汽車的平順性、安全性、操縱穩定性及輪胎的壽命。良好的轉向梯形機構能夠減小行駛阻力，使轉向輕便，并減小輪胎磨損。對轉向梯形機構的運動學相關問題進行研究，并對機構進行優化。這種方法使得結構設計過程更加人性化和科學化，同時為礦用汽車的設計提供參考。

二、 轉向梯形機構運動學分析

轉向梯形機構主要由汽車前軸、轉向節臂和轉向橫拉桿組成，如圖1所示。轉向動力缸推動轉向節臂，轉向節臂再推動轉向橫拉桿，從而帶動轉向橫拉桿的擺動，實現礦用汽車的轉向。

轉向梯形機構的設計直接影響著礦用汽車的轉向性能。合理的轉向梯形機構對提高汽車的安全性至關重要。特別是在礦山這種路況差的運輸環境，如果發生危險，將造成巨大損失，因此安全性要求很高。

圖1 轉向梯形結構

若要保證汽車在轉彎時能夠順利轉彎，兩側轉向輪的偏轉角度必須按一定關系變化，才能使汽車轉向時車輪與地面的相對滑動盡可能小，不發生側滑。轉向梯形機構用來確保汽車轉彎行駛時，所有車輪都能繞同一瞬時轉動中心，在不同的圓周上作無滑動的純滾動，即符合阿克曼理論轉向特性，如圖2所示。設φi、φo分別為內、外轉向車輪轉角，K為兩個轉向節中心點的距離，L為汽車軸距。則理想的內、外轉向車輪的轉角有如下關系：

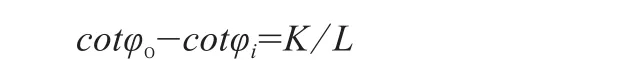
若假設自變量為φo，依據阿克曼理論轉向關系，可以得出因變量φi的理想值為：

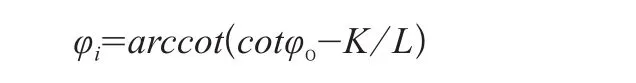
從圖2中我們可以得出最小轉彎半徑Rmin滿足下列關系式：

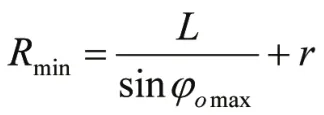
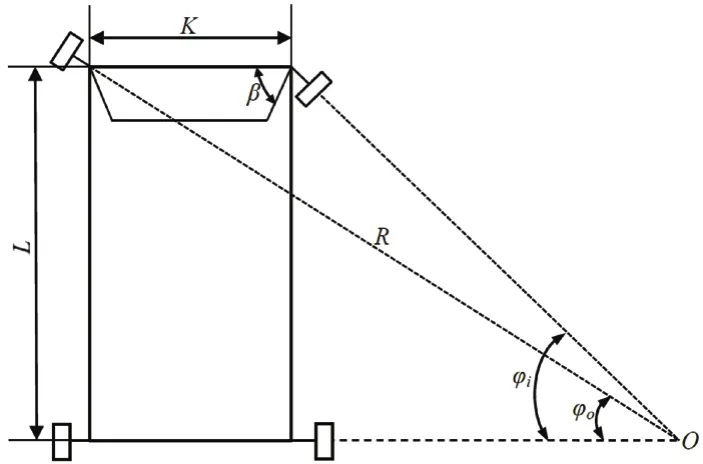
圖2 阿克曼轉向關系圖

式中：r為轉向輪繞主銷轉動半徑（又稱車輪轉臂），設計值為0.92m。在給定最小轉彎半徑Rmin=14.5m的條件下，我們可以計算出外輪最大轉角φomax=27.8°，內側車輪最大轉角理論值為φimax=38.4°。

建立轉向梯形平面數學模型。由圖3可知，只要確定轉向節臂長度m和梯形底角β，就可以確定整個轉向梯形機構。

圖3轉向梯形機構示意圖

設φo為外側車輪轉角，φi’為內側車輪實際轉角，根據圖中幾何關系，可以推導出實際轉向過程中內側車輪轉角與外側車輪轉角之間的關系。在汽車轉向過程中，所設計的轉向梯形機構給出的實際內側車輪轉角φi’應盡可能接近前面推導出來的理論值φi。

根據轉向梯形機構的各項參數，在運動學分析軟件中建立轉向梯形的虛擬樣機模型。仿真模型主要通過構件、標識點、約束、驅動和力等來創建。模型簡化后包括兩個轉向節臂和轉向橫拉桿。添加一個1°/s的旋轉驅動，用來模擬轉向運動。轉向梯形機構的虛擬樣機模型如圖4所示。

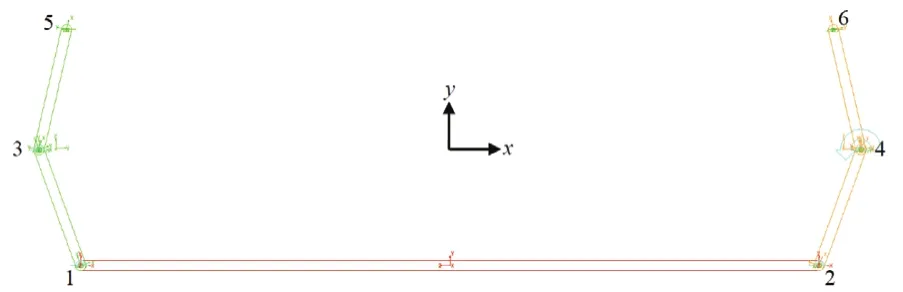
圖4 轉向梯形機構的虛擬樣機模型

圖5是優化前的原始轉向梯形機構轉彎過程中，車輪內外轉角關系和理論轉角關系曲線對比圖。由圖可知，對于初始的轉向梯形結構，轉彎角度逐漸增大時，內輪的實際轉角與理論轉角之間的偏差也在逐漸變大。

從圖6誤差曲線可知，理論轉角與實際轉角的誤差最大值達到1.972°。為提高轉向梯形機構的轉向性能，可以對該機構進行優化設計。

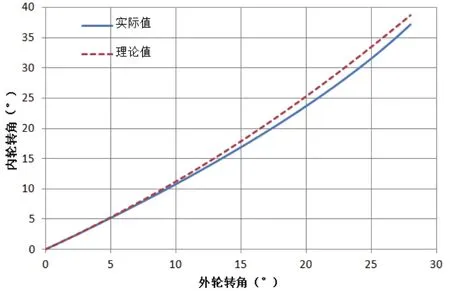
圖5 優化前車輪內外側轉角關系

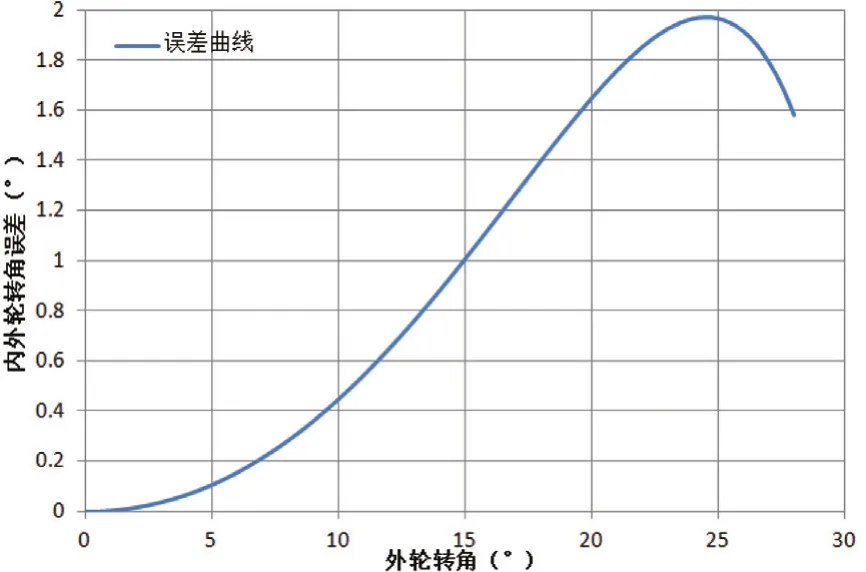
圖6 誤差曲線

三、轉向梯形機構的優化

在運動學分析的基礎上，對轉向梯形機構進行優化，使其最大限度的逼近理想的阿克曼轉向特性，從而提高整車的轉向性能。

優化設計的目標就是要保證在實際轉向過程中，內外輪轉角關系盡量逼近阿克曼轉向特性，即在轉向過程中，實際內輪轉角φi’與理想內輪轉角φi的偏差盡可能的小。從而使轉向輕便并有效減小輪胎的磨損。根據優化設計的原理，給出了優化目標函數為：

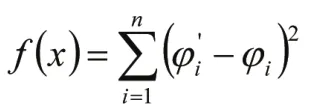
此外，還需要對轉向節臂長m及梯形底角β的取值范圍設置合理的約束。轉向梯形機構必須滿足幾個條件：mmin≤ m ≤ mmax；β-βmin≥ 0。

根據轉向梯形機構設計經驗，轉向節臂的最小值和最大值取mmin=0.11K、mmax=0.15K，梯形底角最小值取βmin=65°。

為方便分析，將圖4中標記點1處的橫縱坐標參數化作為優化變量，等價于將轉向節臂長m以及梯形底角β作為優化變量。優化變量初始值為：x1=-1805，y1=-563。

使用多學科多目標優化軟件對轉向梯形機構進行優化。該軟件將數字技術、推理技術及設計探索技術有效地融合，并把大量需要人工完成的工作由軟件實現自動化處理。使用該軟件提供的設計工具，進行從零部件到系統各層級的性能設計和質量設計，可以高效且科學地完成日益復雜和高難度的產品設計任務。最重要的是，在設計階段保證了產品的可靠性和穩健性。

采用全局探索法進行優化，該方法適應性強，只評價設計點，無須計算任何函數的梯度，因此目標函數可以是多峰性、非線性、非連續、不可微函數。而且能求解全局最優解，避免了集中在局部區域的搜索。優化過程如圖7所示。

圖7 優化過程

優化結果：x1=-1785，y1=-544。此時，梯形底角β=67.53°，轉向節臂長m=588.69mm。（注：優化前梯形底角β=70°，轉向節臂m=599.16mm）優化前后車輪內外轉角關系和理論轉角關系曲線對比如圖8所示。優化前后誤差曲線對比如圖9所示。

從圖8和圖9可以看出，優化后的梯形機構更能逼近理論轉向特性，實際值與理想值能夠很好的吻合，最大轉角誤差從原模型的1.972°減小到0.941°，從而更好地提高轉向性能，使轉向輕便并減小了輪胎磨損和側滑。

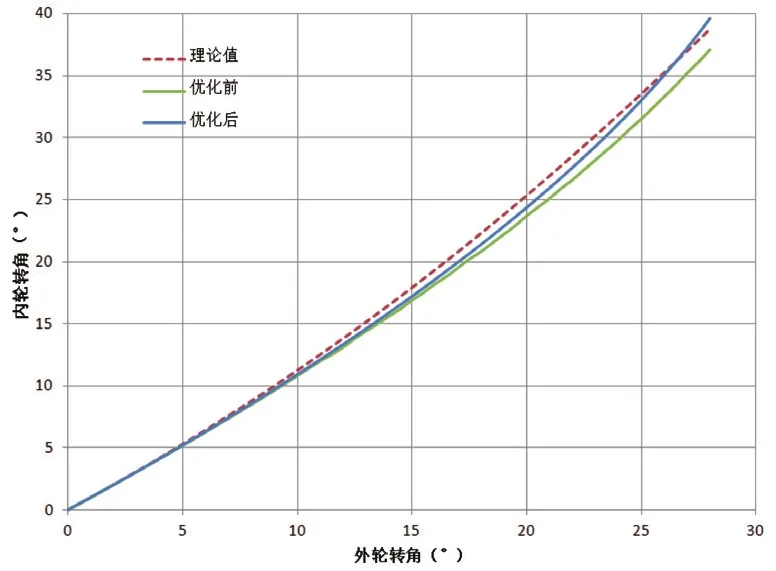
圖8　優化前后內外側轉角關系對比

圖9　優化前后誤差曲線對比

四、結語

轉向梯形機構的設計直接影響著礦用汽車轉向系統性能。本文綜合應用運動學及結構優化的方法對礦用汽車轉向機構進行結構分析和設計研究。

首先通過轉向梯形機構運動學分析。以阿克曼轉角公式為理論依據，運用運動學分析對轉向梯形機構進行了運動學仿真，分析了內外轉向車輪之間的轉角關系以及實際值與理論值之間的偏差，為轉向梯形機構的優化設計提供了理論基礎。接著選取合理的優化目標函數，建立了轉向梯形機構的優化數學模型。對轉向梯形機構進行了優化，使其更加符合阿克曼轉向原理，結果表明，優化后的梯形機構更能逼近理論轉向特性，最大轉角誤差從原模型的1.972°減小到0.941°，從而更好地提高了整車轉向性能，減小了輪胎磨損和側滑。本文的研究實現了對礦用汽車轉向性能的評價，為礦用汽車設計提供了理論參考。